20.  Малютина М.С. Моделирование макроэкономических последствий пенсионной реформы: Автореф. дис. канд. эк. наук: 08.00.13 /МГУ им. М.В. Ломоносова. Эк. фак. – М.: МГУ, 1998. – 16 с.

Влияние пенсионной реформы на капиталовооруженность и экономический рост качественно можно показать с помощью развития модели двух пересекающихся поколений Диамонда (Diamond) в интерпретации Бланшара (Blanchard) и Фишера (Fisher) [80], дополненной Малютиной М. С. предпосылками о растущей эффективности труда, предпочтении свободного времени труду, ограничениями на заимствования, зависимостью пенсионных взносов от уровня заработной платы [47].

Предпосылки модели:

1.Распределение ресурсов и благ происходит по рыночным принципам. Экономические агенты представлены фирмами, максимизирующими прибыль и индивидами, максимизирующими полезность.

2.Каждый индивид живет в течение двух периодов, в первый период жизни он работает, предлагая трудовые ресурсы на рынке труда, и использует полученную плату на текущее потребление и сбережение. Во втором периоде только потребляет блага, используя сбережения предыдущего периода. Численность населения растет с постоянным темпом n.

3.В экономике производится одно благо. Запас капитала определяется накоплениями предыдущего периода. Труд и капитал используется для производства по заданной технологии с постоянной отдачей от масштаба. Производственная функция однородна. Эффективность труда растет с неизменным темпом g. Вознаграждение за труд w_t равно  предельной производительности труда. Ставка процента r_t равна предельной производительности капитала.

4.Функция полезности для индивида сепарабельна по отношению к потреблению в первом и втором периодах жизни. Для анализа влияния пенсионной реформы на рынок капитала рассматривается функция полезности вида U=[u(c_1t)+(1+q)^-1u(c_2t+1)], где c_1t>0 и с_2t+1>0 – величина потребления в год t индивидом в первый и второй периоды жизни соответственно, q – индивидуальный коэффициент дисконтирования полезности отложенного потребления. Для анализа влияния пенсионной реформы на предложение труда рассматривается функция полезности вида U=[u(c_1t)+(1+q)^-1u(c_2t+1)+z(l_t)], где l_t – интенсивность использования индивидом трудовых ресурсов, или относительная продолжительность рабочего времени, s_t- сбережения в период t.

5. Пусть u, z – монотонны, выпуклы вверх и дважды дифференцируемы: u’>0; u’’<0; z’>0; z’’<0.

Для выявления влияния пенсионной реформы на накопление капитала и экономический рост рассмотрим и сравним состояния равновесия в экономике без системы обязательного пенсионного обеспечения и в экономике с накопительным и распределительным пенсионным обеспечением. При отсутствии системы пенсионного обеспечения потребитель решает оптимизационную задачу:

u(c_1t)+(1+q)^-1u(c_2t+1) ® max                                                                                   (3.28)

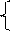c_1t+s_t=w_t                                                                                                                                                        (3.29)

c_2t+1+s_t(1+r_t+1)=w_t

Условия макроэкономического равновесия задаются соотношением:

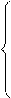-u’(w_t-s_t)+(1+q)^-1(1+r_t+1)u’(s_t(1+r_t+1))=0

k_t+1=s_t/(1+n+g+ng)                                                                                                 (3.30)

w_t=f(k_t)-k_tf’(k_t)

r_t=f’(k_t)

Первое уравнение системы (3.30) определяет равновесие потребителя на микроуровне, второе отражает тот факт, что капиталовооруженность определяется сбережениями предыдущего периода, два последних определяют равновесие на рынке факторов производства,  f(k_t) – функция выпуска на единицу трудовых ресурсов.

При обязательном накопительном пенсионном обеспечении в первый период жизни индивид делает взносы в ПФР в размере d_t=aw_t, а во второй период жизни получает пенсию в размере b_t+1=(1+r_t+1)aw_t, где a – тариф отчисления в ПФР.

Изменяются условия бюджетного ограничения потребителя:

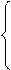c_1t+s_t+ aw_t =w_t

c_2t+1=s_t(1+r_t+1)+ b_t+1                                                                                                (3.31)

b_t+1=(1+r_t+1) aw_t

Система уравнений, описывающая равновесное состояние имеет следующий вид:

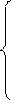-u’(w_t-(s_t+ aw_t))+(1+q)^-1(1+r_t+1)u’((aw_t +s_t)(1+r_t+1))=0

k_t+1=(s_t+ aw_t )/(1+n+g+ng)                                                                                    (3.32)

w_t=f(k_t)-k_tf’(k_t)

r_t=f’(k_t)

Вектор [s_t*, k_t*, w_t*, r_t+1*] решения системы (3.31) является также решением системы (3.32):[s_t*+ aw_t, k_t*, w_t*, r_t+1*]. Устойчивый уровень капиталовооруженности, ставка процента, уровень заработной платы, совокупные сбережения будут одинаковыми при отсутствии ПС и при обязательном накопительном пенсионном обеспечении. При введении ограничений на заимствования обязательные накопления в рамках ПС могут превосходить добровольные сбережения, что означает увеличение уровня капиталовооруженности вследствие введения накопительного обеспечения.

Иной результат получается для экономики с распределительным пенсионным обеспечением. Накопления ПФР отсутствуют, взносы работников целиком распределяются среди пенсионеров.  Отношение между выплатами и взносами принимает вид: b_t+1=(1+n)aw_t.

Изменяются условия бюджетного ограничения потребителя:

c_1t+s_t+ aw_t =w_t

c_2t+1=s_t(1+r_t+1)+ b_t+1                                                                                                (3.33)

b_t+1=(1+n) aw_t

Система уравнений, описывающая равновесное состояние:

-u’(w_t-(s_t+ aw_t))+(1+q)^-1(1+r_t+1)u’((s_t(1+r_t+1)+ (1+n) aw_t)=0

k_t+1=(s_t+ aw_t )/(1+n+g+ng)                                                                                    (3.34)

w_t=f(k_t)-k_tf’(k_t)

r_t=f’(k_t)

 Получаемые социальные пособия сдвигают бюджетное ограничение потребителя, приводят к изменению межвременного распределения благ. Снижается уровень частных сбережений (дs/дa£0). При этом если имеет место положительная связь между уровнем процентных ставок и сбережениями (s’_r), введение распределительного пенсионного обеспечения приводит к уменьшению уровня капиталовооруженности:

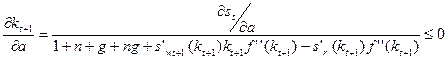                 (3.35)

Таким образом, переход от распределительной пенсионной системы к накопительной будет сопровождаться ростом капиталовооруженности. Эффект сильнее для стран с неразвитыми финансовыми рынками, на которых индивиды чаще сталкиваются с ограничениями на заимствования. Отметим, что большинство стран сейчас находится в условиях дефицита капитала, и пенсионная реформа будет способствовать росту благосостояния будущих поколений [20, с.24].