МИНИСТЕРСТВО
ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ
АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ
ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
КОНТРОЛЬНАЯ РАБОТА
по дисциплине
«СТАТИСТИКА»
Вариант № 13
Выполнила:
Факультет:
Финансово-кредитный
Специальность: Финансовый менеджмент
II высшее образование, 3 курс
Группа
Личное дело
Проверил:
МОСКВА 2008
Имеются
следующие выборочные данные по предприятиям одной из отраслей промышленности в
отчетном году (выборка 5%-ная механическая):
Таблица 1
Исходные данные
|
№ пред-приятия п/п
|
Фонд
за-работной платы, млн. руб.
|
Среднесписочная
численность работников, чел.
|
№ пред-приятия
п/п
|
Фонд
за-работной платы, млн. руб.
|
Среднесписочная
численность работников, чел.
|
|
1
|
11,340
|
162
|
16
|
11,502
|
162
|
|
2
|
8,112
|
156
|
17
|
16,356
|
188
|
|
3
|
15,036
|
179
|
18
|
12,792
|
164
|
|
4
|
19,012
|
194
|
19
|
17,472
|
192
|
|
5
|
13,035
|
165
|
20
|
5,850
|
130
|
|
6
|
8,532
|
158
|
21
|
9,858
|
159
|
|
7
|
26,400
|
220
|
22
|
11,826
|
162
|
|
8
|
17,100
|
190
|
23
|
18,142
|
193
|
|
9
|
12,062
|
163
|
24
|
8,848
|
158
|
|
10
|
9,540
|
159
|
25
|
13,944
|
168
|
|
11
|
13,694
|
167
|
26
|
23,920
|
208
|
|
12
|
21,320
|
205
|
27
|
13,280
|
166
|
|
13
|
16,082
|
187
|
28
|
22,356
|
207
|
|
14
|
10,465
|
161
|
29
|
10,948
|
161
|
|
15
|
4,320
|
120
|
30
|
15,810
|
186
|
Задание 1
Признак – среднесписочная
численность работников.
Число групп – пять.
По исходным данным
(табл.1) необходимо выполнить следующее:
1. Построить статистический ряд
распределения предприятий по Среднесписочной численности работников,
образовав пять групп с равными интервалами.
2. Графическим методом и путем расчётов
определить значения моды и медианы полученного ряда распределения.
3. Рассчитать характеристики ряда
распределения: среднюю арифметическую,
среднее квадратическое отклонение, коэффициент вариации.
4. Вычислить среднюю арифметическую по исходным данным (табл. 1), сравнить её с
аналогичным показателем, рассчитанным в п. 3 для интервального ряда
распределения. Объяснить причину их расхождения.
Сделать выводы по результатам выполнения Задания 1.
Выполнение Задания 1
Целью выполнения данного Задания является изучение состава и
структуры выборочной совокупности предприятий путем построения и анализа
статистического ряда распределения предприятий
по признаку Среднесписочная
численность работников.
1. Построение интервального ряда
распределения предприятий по среднесписочной численности работников
Для построения
интервального вариационного ряда, характеризующего распределение банков по
объему кредитных вложений, необходимо вычислить величину и границы
интервалов ряда.
При построении ряда с
равными интервалами величина интервала h определяется по формуле:
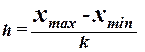 , (1)
, (1)
где 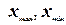 – наибольшее и наименьшее значения
признака в исследуемой совокупности, k- число групп интервального ряда.
– наибольшее и наименьшее значения
признака в исследуемой совокупности, k- число групп интервального ряда.
Число групп k задается в условии задания или
рассчитывается по формуле Г.Стерджесса:
k=1+3,322 lg n, (2)
где n - число единиц
совокупности.
Определение величины
интервала по формуле (1) при заданных k = 5, xmax = 220 чел.,
xmin = 120 чел.:
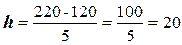 чел.
чел.
При h = 120 чел. границы интервалов ряда распределения имеют следующий вид (табл. 2):
Таблица 2
|
Номер группы
|
Нижняя граница, чел.
|
Верхняя граница, чел.
|
|
1
|
120
|
140
|
|
2
|
140
|
160
|
|
3
|
160
|
180
|
|
4
|
180
|
200
|
|
5
|
200
|
220
|
Для построения интервального ряда необходимо подсчитать число предприятий,
входящих в каждую группу (частоты групп). При этом используется принцип полуоткрытого
интервала [ ), согласно
которому верхние границы интервалов не принадлежат данным интервалам, а
соответствующие им единицы совокупности включаются не в данную группу, а в
следующую.
Процесс группировки единиц совокупности по признаку среднесписочная численность
работников представлен во вспомогательной (разработочной) таблице 3
(графа 4 этой таблицы необходима для построения аналитической группировки в
Задании 2).
Таблица 3
Разработочная таблица для
построения интервального ряда распределения и аналитической группировки
|
Группы предприятий по среднесписочной численности
работников, чел.
|
№ пред-приятия
|
Среднесписочная численность работников, чел.
|
Фонд заработной платы, млн. руб.
|
|
1
|
2
|
3
|
4
|
|
120 - 140
|
15
|
120
|
4,320
|
|
|
20
|
130
|
5,850
|
|
Всего
|
2
|
250
|
10,170
|
|
140- - 160
|
2
|
156
|
8,112
|
|
|
6
|
158
|
8,532
|
|
|
24
|
158
|
8,848
|
|
|
10
|
159
|
9,540
|
|
|
21
|
159
|
9,858
|
|
Всего
|
5
|
790
|
44,890
|
|
160 - 180
|
14
|
161
|
10,465
|
|
|
29
|
161
|
10,948
|
|
|
1
|
162
|
11,340
|
|
|
16
|
162
|
11,502
|
|
|
22
|
162
|
11,826
|
|
|
9
|
163
|
12,062
|
|
|
18
|
164
|
12,792
|
|
|
5
|
165
|
13,035
|
|
|
27
|
166
|
13,280
|
|
|
11
|
167
|
13,694
|
|
|
25
|
168
|
13,944
|
|
|
3
|
179
|
15,036
|
|
Всего
|
12
|
1980
|
149,924
|
|
180 - 200
|
30
|
186
|
15,810
|
|
|
13
|
187
|
16,082
|
|
|
17
|
188
|
16,356
|
|
|
8
|
190
|
17,100
|
|
|
19
|
192
|
17,472
|
|
|
23
|
193
|
18,142
|
|
|
4
|
194
|
19,012
|
|
Всего
|
7
|
1330
|
119,974
|
|
200 - 220
|
12
|
205
|
21,320
|
|
|
28
|
207
|
22,356
|
|
|
26
|
208
|
23,920
|
|
|
7
|
220
|
26,400
|
|
|
4
|
840
|
93,996
|
|
Итого
|
30
|
5190
|
418,954
|
На основе групповых итоговых строк
«Всего» таблицы 3 формируется итоговая таблица 4, представляющая интервальный
ряд распределения предприятий по среднесписочной численности работников.
Таблица 4
Распределение предприятий по среднесписочной
численности работников
|
Номер группы
|
Группы предприятий по среднесписочной численности
работников, чел.,
х
|
Число предприятий,
f.
|
|
1
|
120 – 140
|
2
|
|
2
|
140 - 160
|
5
|
|
3
|
160 - 180
|
12
|
|
4
|
180 - 200
|
7
|
|
5
|
200 - 220
|
4
|
|
|
Итого
|
30
|
Помимо частот групп в абсолютном
выражении в анализе интервальных рядов используются ещё три характеристики ряда
распределения - частоты групп в
относительном выражении, накопленные (кумулятивные) частоты Sj, получаемые путем последовательного
суммирования частот всех предшествующих (j-1) интервалов, и накопленные
частости, рассчитываемые по формуле 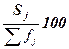 .
.
Таблица 5
Структура предприятий по среднесписочной
численности работников
|
Номер группы
|
Группы предприятий по среднесписочной численности
работников, чел.
|
Число предприятий, 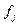
|
Накопленная частота,
Sj
|
Накопленная частоcть, %
|
|
в абсолют-ном выра-жении
|
в % к итогу
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
120 – 140
|
2
|
6,7
|
2
|
6,7
|
|
2
|
140 - 160
|
5
|
16,7
|
7
|
23,3
|
|
3
|
160 - 180
|
12
|
40
|
19
|
63,3
|
|
4
|
180 - 200
|
7
|
23,3
|
26
|
86,7
|
|
5
|
200 - 220
|
4
|
13,3
|
30
|
100,0
|
|
|
Итого
|
30
|
100,0
|
|
|
Вывод. Анализ интервального ряда
распределения изучаемой совокупности предприятий показывает, что распределение предприятий
по среднесписочной численности работников не является равномерным: преобладают предприятия
со среднесписочной численностью от 160 чел. до 180 чел. (это 12 предприятий,
доля которых составляет 40%); 23,3% предприятий имеют среднесписочную численность менее 140 млн.
руб., а 63,3% - менее 180 чел.
1.2. Нахождение моды и медианы полученного
интервального ряда распределения графическим методом и путем расчетов
Мода и медиана являются структурными
средними величинами, характеризующими (наряду со средней
арифметической) центр распределения единиц совокупности по изучаемому признаку.
Моду Мо можно определить графическим методом
по гистограмме ряда (рис.1).
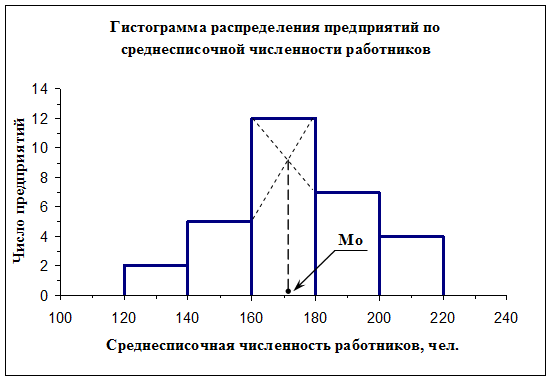
Рис. 1 Определение моды графическим
методом
Конкретное значение моды
для интервального ряда рассчитывается по формуле:
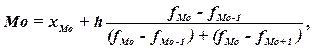 (3)
(3)
где хМo – нижняя
граница модального интервала,
h –величина модального интервала,
fMo – частота модального интервала,
fMo-1 – частота интервала, предшествующего
модальному,
fMo+1 – частота интервала, следующего за модальным.
Согласно таблице 3
модальным интервалом построенного ряда является интервал 160 – 180 чел., так
как его частота максимальна (f3 = 12).
Расчет моды по формуле
(3):
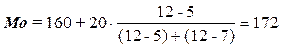 чел.
чел.
Вывод. Для рассматриваемой совокупности предприятий наиболее распространенная среднесписочная
численность работников характеризуется средней величиной 172 чел.
Медиану Ме
можно определить графическим методом по кумулятивной кривой (рис. 2). Кумулята
строится по накопленным частотам (табл. 5, графа 5).
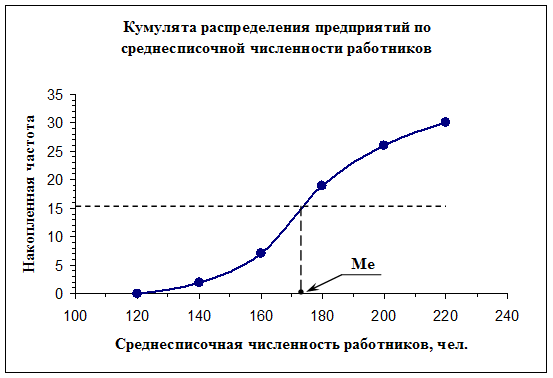
Рис. 2. Определение медианы
графическим методом
Конкретное значение
медианы для интервального ряда рассчитывается по формуле:
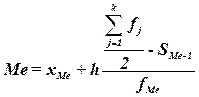 , (4)
, (4)
где хМе– нижняя граница
медианного интервала,
h – величина медианного интервала,
fМе – частота медианного интервала,
SMе-1 – кумулятивная (накопленная) частота
интервала, предшествующего медианному;
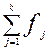 - сумма всех частот.
- сумма всех частот.
Определим медианный
интервал, для чего используются накопленные частоты (или частости) из таблицы 5
(графа 5). Медианным интервалом является интервал 160 – 180 чел., так как
именно в этом интервале накопленная частота Sj = 19 впервые превышает величину,
равную половине численности единиц совокупности (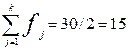 ).
).
Расчет значения медианы
по формуле (4):
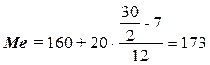 чел.
чел.
Вывод. В рассматриваемой совокупности предприятий
половина предприятий имеют в среднем списочную численность работников не более
173 чел., а другая половина – не менее 173 чел.
3. Расчет
характеристик ряда распределения.
Для расчета характеристик ряда распределения 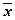 , σ, σ2, Vσ на основе табл. 5 строится
вспомогательная таблица 6 (
, σ, σ2, Vσ на основе табл. 5 строится
вспомогательная таблица 6 (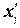 – середина j-го интервала).
– середина j-го интервала).
Таблица 6
Расчетная таблица для
нахождения характеристик ряда распределения
|
Группы предприятий по среднесписочной численности
работников, чел.
|
Середина интервала,
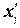
|
Число предпри-яитий,
fj
|
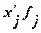
|
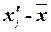
|
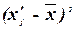
|
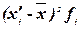
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
120 – 140
|
130
|
2
|
260
|
-44
|
1936
|
3872
|
|
140 - 160
|
150
|
5
|
750
|
-24
|
576
|
2880
|
|
160 - 180
|
170
|
12
|
2040
|
-4
|
16
|
192
|
|
180 - 200
|
190
|
7
|
1330
|
16
|
256
|
1792
|
|
200 - 220
|
210
|
4
|
840
|
36
|
1296
|
5184
|
|
Итого
|
|
30
|
5220
|
|
|
13920
|
Расчет средней арифметической взвешенной:
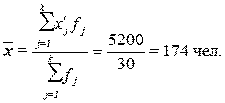 (5)
(5)
Расчет среднего квадратического
отклонения:
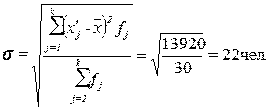 (6)
(6)
Расчет дисперсии:
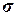 2 =464
2 =464
Расчет коэффициента вариации:
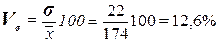 (7)
(7)
Вывод. Анализ полученных значений показателей 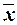 и
и 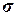 говорит о том, что средняя величина
среднесписочной численности работников предприятий составляет 173 чел.,
отклонение от средней величины в ту или иную сторону составляет в среднем 22 чел.
(или 12,6%), наиболее характерные значения среднесписочной численности
работников находятся в пределах от 152 чел. до 196 чел. (диапазон
говорит о том, что средняя величина
среднесписочной численности работников предприятий составляет 173 чел.,
отклонение от средней величины в ту или иную сторону составляет в среднем 22 чел.
(или 12,6%), наиболее характерные значения среднесписочной численности
работников находятся в пределах от 152 чел. до 196 чел. (диапазон 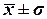 ).
).
Значение Vσ = 12,6% не превышает 33%,
следовательно, вариация среднесписочной численности работников в исследуемой
совокупности предприятий незначительна и совокупность по данному признаку
качественно однородна. Расхождение между значениями 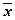 , Мо и Ме незначительно (
, Мо и Ме незначительно (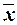 =174 чел., Мо=172
чел., Ме=173 чел.), что подтверждает
вывод об однородности совокупности предприятий. Таким образом, найденное
среднее значение списочной численности работников предприятий (174 чел.)
является типичной, надежной характеристикой исследуемой совокупности предприятий.
=174 чел., Мо=172
чел., Ме=173 чел.), что подтверждает
вывод об однородности совокупности предприятий. Таким образом, найденное
среднее значение списочной численности работников предприятий (174 чел.)
является типичной, надежной характеристикой исследуемой совокупности предприятий.
4. Вычисление средней
арифметической по исходным данным
Для расчета применяется
формула средней арифметической простой:
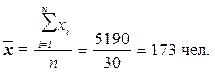 (8)
(8)
Причина расхождения
средних величин, рассчитанных по формулам (8) и (5), заключается в том, что по
формуле (8) средняя определяется по фактическим
значениям исследуемого признака
для всех 30-ти предприятий, а по формуле (5) средняя
вычисляется для интервального ряда, когда в качестве значений признака берутся
середины интервалов 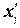 и, следовательно, значение средней будет менее
точным (за исключением случая равномерного распределения значений признака
внутри каждой группы).
и, следовательно, значение средней будет менее
точным (за исключением случая равномерного распределения значений признака
внутри каждой группы).
Задание 2
По исходным данным (табл.
1) с использованием результатов выполнения Задания 1 необходимо:
1. Установить наличие и характер
корреляционной связи между признаками Среднесписочная
численность работников и Фонд
заработной платы, образовав по каждому признаку пять групп с равными
интервалами, используя методы:
а) аналитической группировки;
б) корреляционной
таблицы.
2. Оценить тесноту корреляционной связи,
используя коэффициент детерминации и эмпирическое корреляционное отношение.
Сделать выводы по результатам выполнения Задания 2.
Выполнение Задания 2
Целью выполнения
данного Задания
является выявление наличия корреляционной связи между факторным и
результативным признаками, установление направления связи и оценка ее тесноты.
По условию Задания 2 факторным является признак Среднесписочная численность работников (X), результативным – признак
Фонд заработной платы (Y).
1. Установление
наличия и характера связи между признаками Среднесписочная
численность работников и Фонд
заработной платы методами аналитической группировки и корреляционной
таблицы
1а. Применение метода аналитической группировки.
При использовании метода аналитической группировки строится
интервальный ряд распределения единиц совокупности по факторному признаку Х и для каждой j-ой группы ряда определяется среднегрупповое
значение 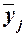 результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения
результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения 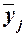 систематически
возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
систематически
возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.
Используя разработочную таблицу 3, строим аналитическую
группировку, характеризующую зависимость между факторным признаком Х – среднесписочная численность
работников и результативным
признаком Y – фонд
заработной платы. Макет аналитической таблицы имеет следующий вид
(табл. 7):
Таблица 7
Зависимость фонда заработной платы от среднесписочной
численности работников.
|
Номер группы
|
Группы предприятий по среднесписочной численности
работников, чел.
|
Число предпри-ятий
|
Фонд заработной платы, млн. руб.
|
|
всего
|
в среднем на одно предприятие
|
|
1
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
4
|
|
|
|
|
|
5
|
|
|
|
|
|
Итого
|
|
|
|
|
Групповые средние значения 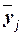 получаем из
таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную
аналитическую группировку представляет табл. 8.
получаем из
таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную
аналитическую группировку представляет табл. 8.
Таблица 8
Зависимость фонда заработной платы от среднесписочной
численности работников.
|
Номер группы
|
Группы предприятий по среднесписочной численности
работников, чел.
|
Число предпри-ятий
|
Фонд заработной платы, млн. руб.
|
|
всего
|
в среднем на одно предприятие
|
|
1
|
2
|
3
|
4
|
5 = 4 / 3
|
|
1
|
120 – 140
|
2
|
10.170
|
5.085
|
|
2
|
140 - 160
|
5
|
44.890
|
8.978
|
|
3
|
160 - 180
|
12
|
149.924
|
12.494
|
|
4
|
180 - 200
|
7
|
119.974
|
17.139
|
|
5
|
200 - 220
|
4
|
93.996
|
23.499
|
|
Итого
|
|
30
|
418.954
|
13.965
|
Вывод. Анализ данных таблицы 8 показывает,
что с увеличением среднесписочной численности работников от группы к группе
систематически возрастает и средний фонд заработной платы по каждой группе предприятий,
что свидетельствует о наличии прямой корреляционной связи между исследуемыми
признаками.
1б. Применение метода
корреляционной таблицы.
Корреляционная таблица
представляет собой комбинацию двух рядов распределения. Строки таблицы
соответствуют группировке единиц совокупности по факторному признаку Х, а графы – группировке единиц по
результативному признаку Y. На пересечении j-ой строки и k-ой графы указывается число единиц
совокупности, входящих в j-ый интервал по факторному признаку и
в k-ый
интервал по результативному признаку.
Для построения
корреляционной таблицы необходимо знать величины и границы интервалов по двум
признакам X и Y. Величина интервала и границы интервалов для
факторного признака Х –
Среднесписочная численность работников
известны из табл. 8. Для результативного признака Y – Фонд заработной платы
величина интервала определяется по формуле (1) при k = 5, уmax = 26,4 млн. руб., уmin = 4,32 млн.
руб.:
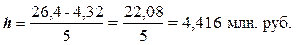
Границы
интервалов ряда распределения результативного признака Y имеют следующий вид (табл.
9):
Таблица 9
|
Номер группы
|
Нижняя граница,
млн. руб.
|
Верхняя граница,
млн. руб.
|
|
1
|
4,320
|
8,736
|
|
2
|
8,736
|
13,152
|
|
3
|
13,152
|
17,568
|
|
4
|
17,568
|
21,984
|
|
5
|
21,984
|
26,400
|
Подсчитывая с использованием принципа
полуоткрытого
интервала [ ) число предприятий,
входящих в каждую группу (частоты групп), получаем интервальный ряд распределения
результативного признака (табл. 10).
Таблица 10
Распределение предприятий по
фонду заработной платы
|
Группы предприятий по фонду заработной платы,
млн.руб.,
х
|
Число предприятий,
fj
|
|
4,320 – 8,736
|
4
|
|
8,736 – 13,152
|
11
|
|
13,152 – 17,568
|
9
|
|
17,568 – 21,984
|
3
|
|
21,984 – 26,400
|
3
|
|
Итого
|
30
|
Используя группировки по факторному и
результативному признакам, строим корреляционную таблицу (табл. 11).
Таблица 11
Корреляционная таблица зависимости фонда заработной
платы от среднесписочной численности работников.
|
Группы предприятий по среднесписочной численности
работников, чел.
|
Группы предприятий по фонду заработной платы,
млн.руб.,
|
|
4,320 – 8,736
|
8,736 – 13,152
|
13,152 – 17,568
|
17,568 – 21,984
|
21,984 – 26,400
|
Итого
|
|
120 – 140
|
2
|
|
|
|
|
2
|
|
140 - 160
|
2
|
3
|
|
|
|
5
|
|
160 - 180
|
|
8
|
4
|
|
|
12
|
|
180 - 200
|
|
|
5
|
2
|
|
7
|
|
200 - 220
|
|
|
|
1
|
3
|
4
|
|
Итого
|
4
|
11
|
9
|
3
|
3
|
30
|
Вывод. Анализ данных таблицы 11 показывает,
что распределение частот групп произошло вдоль диагонали, идущей из левого
верхнего угла в правый нижний угол таблицы. Это свидетельствует о наличии
прямой корреляционной связи между фондом заработной платы и среднесписочной
численностью работников.
2. Измерение
тесноты корреляционной связи с использованием коэффициента детерминации и
эмпирического корреляционного отношения
Эмпирический
коэффициент детерминации 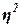 оценивает, насколько
вариация результативного признака Y
объясняется вариацией фактора Х
(остальная часть вариации Y
объясняется вариацией прочих факторов). Показатель
оценивает, насколько
вариация результативного признака Y
объясняется вариацией фактора Х
(остальная часть вариации Y
объясняется вариацией прочих факторов). Показатель 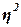 рассчитывается как
доля межгрупповой дисперсии в общей дисперсии по формуле:
рассчитывается как
доля межгрупповой дисперсии в общей дисперсии по формуле:
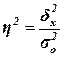 , (9)
, (9)
где 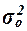 – общая дисперсия
признака Y,
– общая дисперсия
признака Y,
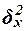 – межгрупповая
(факторная) дисперсия признака Y.
– межгрупповая
(факторная) дисперсия признака Y.
Общая
дисперсия 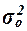 характеризует вариацию
результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель
вычисляется по формуле
характеризует вариацию
результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель
вычисляется по формуле
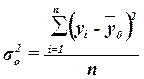 , (10)
, (10)
где yi – индивидуальные значения
результативного признака;
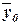 – общая средняя значений результативного признака;
– общая средняя значений результативного признака;
n – число единиц совокупности.
Общая средняя 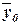 вычисляется как
средняя арифметическая простая по всем единицам совокупности:
вычисляется как
средняя арифметическая простая по всем единицам совокупности:
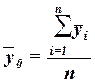 (11)
(11)
или как средняя взвешенная по частоте групп интервального
ряда:
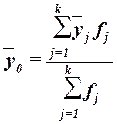 (12)
(12)
Для вычисления 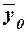 удобно использовать
формулу (11), так как в таблице 8 (графы 3 и 4 итоговой строки) имеются
значения числителя и знаменателя формулы.
удобно использовать
формулу (11), так как в таблице 8 (графы 3 и 4 итоговой строки) имеются
значения числителя и знаменателя формулы.
Расчет 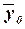 по формуле (11):
по формуле (11):
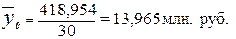
Для расчета общей дисперсии 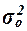 применяется
вспомогательная таблица 12.
применяется
вспомогательная таблица 12.
Таблица 12
Вспомогательная таблица для расчета общей дисперсии.
|
№ пред-приятия п/п
|
Фонд зара-ботной платы, млн. руб.
|
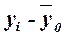
|
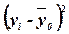
|
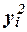
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
11.340
|
-2.625
|
6.891
|
128.596
|
|
2
|
8.112
|
-5.853
|
34.258
|
65.805
|
|
3
|
15.036
|
1.071
|
1.147
|
226.081
|
|
4
|
19.012
|
5.047
|
25.472
|
361.456
|
|
5
|
13.035
|
-0.930
|
0.865
|
169.911
|
|
6
|
8.532
|
-5.433
|
29.517
|
72.795
|
|
7
|
26.400
|
12.435
|
154.629
|
696.960
|
|
8
|
17.100
|
3.135
|
9.828
|
292.410
|
|
9
|
12.062
|
-1.903
|
3.621
|
145.492
|
|
10
|
9.540
|
-4.425
|
19.581
|
91.012
|
|
11
|
13.694
|
-0.271
|
0.073
|
187.526
|
|
12
|
21.320
|
7.355
|
54.096
|
454.542
|
|
13
|
16.082
|
2.117
|
4.482
|
258.631
|
|
14
|
10.465
|
-3.500
|
12.250
|
109.516
|
|
15
|
4.320
|
-9.645
|
93.026
|
18.662
|
|
16
|
11.502
|
-2.463
|
6.066
|
132.296
|
|
17
|
16.356
|
2.391
|
5.717
|
267.519
|
|
18
|
12.792
|
-1.173
|
1.376
|
163.635
|
|
19
|
17.472
|
3.507
|
12.299
|
305.271
|
|
20
|
5.850
|
-8.115
|
65.853
|
34.223
|
|
21
|
9.858
|
-4.107
|
16.867
|
97.180
|
|
22
|
11.826
|
-2.139
|
4.575
|
139.854
|
|
23
|
18.142
|
4.177
|
17.447
|
329.132
|
|
24
|
8.848
|
-5.117
|
26.184
|
78.287
|
|
25
|
13.944
|
-0.021
|
0.000
|
194.435
|
|
26
|
23.920
|
9.955
|
99.102
|
572.166
|
|
27
|
13.280
|
-0.685
|
0.469
|
176.358
|
|
28
|
22.356
|
8.391
|
70.409
|
499.791
|
|
29
|
10.948
|
-3.017
|
9.102
|
119.859
|
|
30
|
15.810
|
1.845
|
3.404
|
249.956
|
|
Итого
|
418.954
|
0.004
|
788.609
|
6639.357
|
Расчет общей дисперсии по формуле (10):
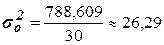
Общая дисперсия может быть также рассчитана по формуле
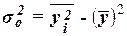 ,
,
где 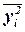 – средняя из квадратов
значений результативного признака,
– средняя из квадратов
значений результативного признака,
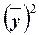 – квадрат средней
величины значений результативного признака.
– квадрат средней
величины значений результативного признака.
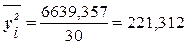
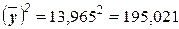
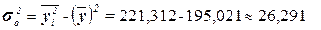
Межгрупповая дисперсия 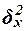 измеряет систематическую вариацию результативного признака, обусловленную
влиянием признака-фактора Х (по
которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется
в отклонении групповых средних
измеряет систематическую вариацию результативного признака, обусловленную
влиянием признака-фактора Х (по
которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется
в отклонении групповых средних 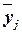 от общей средней
от общей средней 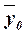 . Показатель
. Показатель 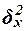 вычисляется по формуле
вычисляется по формуле
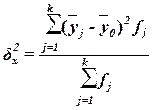 , (13)
, (13)
где 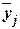 –групповые средние,
–групповые средние,
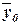 – общая средняя,
– общая средняя,
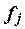 –число единиц в j-ой группе,
–число единиц в j-ой группе,
k – число групп.
Для расчета межгрупповой
дисперсии 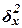 строится вспомогательная таблица 13. При этом
используются групповые средние значения
строится вспомогательная таблица 13. При этом
используются групповые средние значения 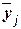 из таблицы 8
(графа 5).
из таблицы 8
(графа 5).
Таблица 13
Вспомогательная таблица для расчета межгрупповой дисперсии
|
Группы предприятий по среднесписочной численности
работников, чел.
|
Число пред-приятий, 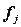
|
Среднее значение 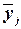 в группе в группе
|
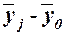
|
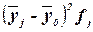
|
|
1
|
2
|
3
|
4
|
5
|
|
120 – 140
|
2
|
5.085
|
-8.880
|
157.709
|
|
140 - 160
|
5
|
8.978
|
-4.987
|
124.351
|
|
160 - 180
|
12
|
12.494
|
-1.471
|
25.978
|
|
180 - 200
|
7
|
17.139
|
3.174
|
70.526
|
|
200 - 220
|
4
|
23.499
|
9.534
|
363.589
|
|
Итого
|
30
|
|
|
742.152
|
Расчет межгрупповой
дисперсии 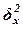 по формуле (11):
по формуле (11):
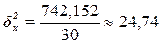
Расчет эмпирического
коэффициента детерминации 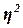 по формуле (9):
по формуле (9):
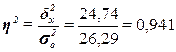 или 94,1%
или 94,1%
Вывод. 94,1% вариации фонда заработной
платы предприятий обусловлено вариацией среднесписочной численности работников,
а 5,9% – влиянием прочих неучтенных
факторов.
Эмпирическое корреляционное отношение 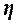 оценивает тесноту
связи между факторным и результативным признаками и вычисляется по формуле:
оценивает тесноту
связи между факторным и результативным признаками и вычисляется по формуле:
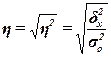 (14)
(14)
Значение показателя изменяются в пределах 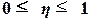 . Чем ближе значение
. Чем ближе значение 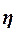 к 1, тем теснее связь
между признаками. Для качественной оценки тесноты связи на основе
к 1, тем теснее связь
между признаками. Для качественной оценки тесноты связи на основе 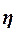 служит шкала Чэддока
(табл. 14):
служит шкала Чэддока
(табл. 14):
Таблица 14
Шкала Чэддока
|
h
|
0,1 – 0,3
|
0,3 – 0,5
|
0,5 – 0,7
|
0,7 – 0,9
|
0,9 – 0,99
|
|
Характеристика
силы связи
|
Слабая
|
Умеренная
|
Заметная
|
Тесная
|
Весьма тесная
|
Расчет
эмпирического корреляционного отношения 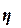 по формуле (14):
по формуле (14):
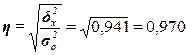 или 97%
или 97%
Вывод. Согласно шкале Чэддока связь между фондом
заработной платы и среднесписочной численностью работников предприятий является
весьма тесной.
Задание 3
По результатам выполнения
Задания 1 с вероятностью 0,954 необходимо определить:
1. Ошибку выборки средней списочной
численности работников и границы, в которых будет находиться средняя в
генеральной совокупности.
2.
Ошибку
выборки доли организаций со средней списочной численностью работников 180 чел.
и выше, а также границы, в которых будет находиться генеральная доля.
Выполнение Задания 3
Целью выполнения
данного Задания
является определение для генеральной совокупности предприятий границ, в которых
будут находиться величина средней списочной численности работников предприятия
и доля предприятий со среднесписочной численностью работников не менее 180 чел.
1. Определение
ошибки выборки для средней списочной численности работников и границ, в которых
будет находиться средняя в генеральной совокупности.
Применение выборочного
метода наблюдения всегда связано с установлением степени достоверности оценок
показателей генеральной совокупности, полученных на основе значений
показателей выборочной совокупности. Достоверность этих оценок зависит от
репрезентативности выборки, т.е. от того, насколько полно и адекватно представлены в выборке статистические
свойства генеральной совокупности. Как
правило, генеральные и выборочные характеристики не совпадают, а отклоняются на
некоторую величину ε, которую
называют ошибкой выборки (ошибкой репрезентативности).
Значения признаков
единиц, отобранных из генеральной совокупности в выборочную, всегда случайны,
поэтому и статистические характеристики выборки случайны, следовательно, и
ошибки выборки также случайны. Ввиду этого принято вычислять два вида ошибок -
среднюю 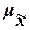 и предельную
и предельную 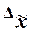 .
.
Средняя ошибка
выборки 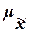 - это среднее
квадратическое отклонение всех возможных значений выборочной средней от
генеральной средней, т.е. от своего математического ожидания M[
- это среднее
квадратическое отклонение всех возможных значений выборочной средней от
генеральной средней, т.е. от своего математического ожидания M[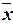 ].
].
Величина
средней ошибки выборки рассчитывается дифференцированно
(по различным формулам) в зависимости от вида
и способа отбора единиц из генеральной совокупности в выборочную.
Для
собственно-случайной и механической выборки с бесповторным способом отбора
средняя ошибка 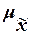 выборочной средней
выборочной средней 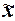 определяется по формуле:
определяется по формуле:
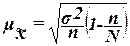 ,
(15)
,
(15)
где 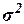 – общая дисперсия
выборочных значений признаков,
– общая дисперсия
выборочных значений признаков,
N – число единиц в генеральной
совокупности,
n – число единиц в выборочной
совокупности.
Предельная ошибка выборки 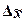 определяет границы, в пределах которых
будет находиться генеральная средняя:
определяет границы, в пределах которых
будет находиться генеральная средняя:
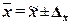 ,
,
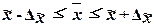 , (16)
, (16)
где 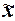 – выборочная средняя,
– выборочная средняя,
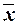 – генеральная средняя.
– генеральная средняя.
Границы задают доверительный
интервал генеральной средней, т.е. случайную область значений, которая
с вероятностью Р гарантированно содержит значение генеральной средней.
Эту вероятность Р называют доверительной
вероятностью или уровнем
надёжности.
Предельная ошибка выборки
Δ кратна средней ошибке µ
с коэффициентом
кратности t (называемым также коэффициентом доверия), который зависит от значения
доверительной вероятности Р. Для
предельной ошибки выборочной средней 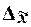 это теоретическое
положение выражается формулой:
это теоретическое
положение выражается формулой:
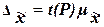 (17)
(17)
Значения t вычислены заранее для различных
доверительных вероятностей Р и протабулированы (таблицы
функции Лапласа Ф). Для наиболее часто используемых уровней надежности Р
значения t
задаются следующим образом (табл. 15):
Таблица 15
|
Доверительная вероятность P
|
0,683
|
0,866
|
0,954
|
0,988
|
0,997
|
0,999
|
|
Значение t
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
По условию выборочная совокупность
насчитывает 30 предприятий, выборка 5%-ная механическая, следовательно, генеральная
совокупность включает 600 предприятий. Выборочная средняя 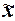 и дисперсия
и дисперсия 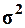 определены в Задании 1
(п. 3). Значения параметров, необходимых для решения задачи, представлены в
таблице 16:
определены в Задании 1
(п. 3). Значения параметров, необходимых для решения задачи, представлены в
таблице 16:
Таблица 16
|
Р
|
t
|
n
|
N
|
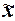
|
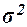
|
|
0,954
|
2
|
30
|
600
|
174
|
464
|
Расчет средней ошибки выборки по формуле (15):
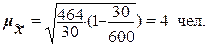
Расчет предельной ошибки
выборки по формуле (17):
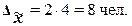
Определение по формуле
(16) доверительного интервала для генеральной средней:
174- 8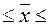 174+8,
174+8,
166 чел. 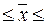 182 чел.
182 чел.
Вывод. На основании проведенного
выборочного обследования предприятий региона с вероятностью 0,954 можно
утверждать, что для генеральной совокупности предприятий величина средней списочная
численность работников предприятий находится в пределах от 166 чел. до 182 чел.
2. Определение
ошибки выборки для доли организаций со средней списочной численностью
работников 180 чел. и выше, а также границ, в которых будет находиться
генеральная доля.
Доля
единиц выборочной совокупности, обладающих тем или иным заданным свойством,
выражается формулой:
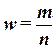 , (18)
, (18)
где
m – число
единиц совокупности, обладающих заданным свойством;
n – общее число единиц в совокупности.
Для
собственно-случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки 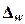 доли единиц,
обладающих заданным свойством, рассчитывается по формуле
доли единиц,
обладающих заданным свойством, рассчитывается по формуле
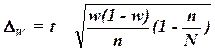 , (19)
, (19)
где
w – доля
единиц совокупности, обладающих заданным свойством;
(1-w) – доля единиц совокупности, не
обладающих заданным свойством,
N – число единиц в генеральной
совокупности,
n– число единиц в выборочной
совокупности.
Предельная
ошибка выборки 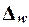 определяет границы, в пределах которых
будет находиться генеральная доля р единиц, обладающих заданным
свойством:
определяет границы, в пределах которых
будет находиться генеральная доля р единиц, обладающих заданным
свойством:
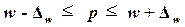 (20)
(20)
По условию Задания 3
исследуемым свойством является равенство
или превышение среднесписочной численности работников предприятия величины 180
чел.
Число предприятий
с заданным свойством определяется из таблицы 3 (графа 3): m=11.
Расчет
выборочной доли по формуле (18):
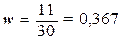
Расчет по формуле (19)
предельной ошибки выборки для доли:
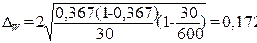
Определение по формуле
(20) доверительного интервала генеральной доли:
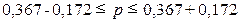
0,195 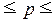 0,539
0,539
или
19,5% 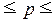 53,9%
53,9%
Вывод. С
вероятностью 0,954 можно утверждать, что в генеральной совокупности предприятий
доля предприятий со средней
списочной численностью работников 180 чел. и выше будет находиться в пределах
от 19,5% до 53,9%.
Задание 4.
Имеются
следующие данные по двум организациям (табл. 17):
Таблица
17
Исходные
данные
|
№ организации п/п
|
Базисный период
|
Отчетный период
|
|
Средняя заработная плата, руб.
|
Среднесписочная численность работников, чел.
|
Средняя заработная плата, руб.
|
Фонд заработной платы, тыс. руб..
|
|
1
|
5000
|
100
|
6500
|
682,5
|
|
2
|
5600
|
100
|
8000
|
760,0
|
Определите:
1.
Индексы динамики
средней заработной платы по каждой организации.
Результаты расчетов представьте в таблице.
2.
По двум
организациям вместе:
- индекс
средней заработной платы переменного, постоянного состава, структурных сдвигов;
- абсолютное
изменение средней заработной платы в целом и за счет отдельных факторов;
Абсолютное изменение фонда заработной
платы вследствие изменения среднесписочной численности работников, средней
заработной платы и двух факторов вместе.
Сделайте
выводы.
1.
Определение индексов динамики средней заработной платы
по каждой организации
Средняя заработная
плата Зср рассчитывается как отношение фонда
заработной платы Фз, начисленного за месяц, к среднесписочной
численности работников Чср :
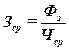 , (21)
, (21)
Для расчета индексов
динамики средней заработной платы по каждой организации используются
индивидуальные индексы средней заработной платы:
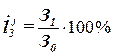 , (22)
, (22)
где З1 и З0– средняя заработная плата j-ой организации в отчетном и базовом
периоде соответственно.
Индексы динамики средней заработной
платы по каждой организации представлены в таблице 18.
Таблица 18
Динамика
средней заработной платы
|
№
организа-ции п/п
|
Средняя заработная плата, руб.
|
Абсолютное изменение средней заработной платы, руб.
|
Индекс динамики средней заработной платы ( iЗ)
|
|
Базисный период
|
Отчетный период.
|
|
1
|
2
|
3
|
4 = 3 - 2
|
5 = 3 / 2
|
|
1
|
5000
|
6500
|
1500
|
1,300
|
|
2
|
5600
|
8000
|
2400
|
1,428
|
Вывод. Средняя заработная плата в отчетном
периоде по сравнению с базисным в 1-ой организации она увеличилась на 30% (или
на 1500 руб.), а во 2-ой – на 43% (или на 2400 руб.).
2.1 Определение индексов
средней заработной платы переменного, постоянного состава, структурных сдвигов
по двум организациям вместе
Динамика
уровней средней заработной платы по всей совокупности организаций (в данном случае по двум
организациям) анализируется с помощью индексов переменного состава, постоянного
состава и индекса структурных сдвигов.
Индекс
переменного состава заработной платы 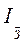 характеризует
изменение среднего уровня заработной платы в отчетном периоде по сравнению с
базисным, в зависимости от изменения средней заработной платы в каждой из
организаций и удельного веса доли предприятий с различным уровнем оплаты труда.
Для его исчисления берутся значения фондов начисленной заработной платы
отдельных категорий работников или всего персонала за отчетный и базовый периоды
(Ф1
и Ф0
), среднесписочная численность отдельных категорий работников или всего
персонала в отчетном и базовом периодах (Ч1 и Ч0 ) и средняя
заработная плата по группам персонала или по предприятиям и отраслям (З1
и З0
). Индекс рассчитывается следующим образом:
характеризует
изменение среднего уровня заработной платы в отчетном периоде по сравнению с
базисным, в зависимости от изменения средней заработной платы в каждой из
организаций и удельного веса доли предприятий с различным уровнем оплаты труда.
Для его исчисления берутся значения фондов начисленной заработной платы
отдельных категорий работников или всего персонала за отчетный и базовый периоды
(Ф1
и Ф0
), среднесписочная численность отдельных категорий работников или всего
персонала в отчетном и базовом периодах (Ч1 и Ч0 ) и средняя
заработная плата по группам персонала или по предприятиям и отраслям (З1
и З0
). Индекс рассчитывается следующим образом:
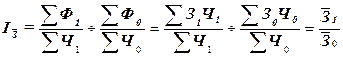 , (23)
, (23)
Индекс
постоянного состава заработной платы 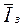 рассчитывается в том
случае, если необходимо отразить только изменение среднего уровня заработной
платы в отчетном периоде по сравнению с базовым без учета структурного фактора
(изменения доли организаций с различным уровнем заработной платы в общем фонде
заработной платы):
рассчитывается в том
случае, если необходимо отразить только изменение среднего уровня заработной
платы в отчетном периоде по сравнению с базовым без учета структурного фактора
(изменения доли организаций с различным уровнем заработной платы в общем фонде
заработной платы):
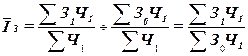 , (24)
, (24)
Если
необходимо зафиксировать влияние структурного фактора на изменение среднего
уровня заработной платы, то рассчитывается индекс структурных
сдвигов 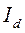 :
:
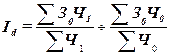 , (25)
, (25)
Между
индексами постоянного, переменного состава и структурных сдвигов существует
взаимосвязь:
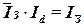 ,
(26)
,
(26)
Для расчета
общей индексов средней заработной платы
по двум организациям применяется вспомогательная таблица 19.
Таблица 19
Вспомогательная таблица для расчета индексов средней
заработной платы
|
№ орга-низа-ции п/п
|
Базисный период
|
Отчетный период
|
Фонд
заработной платы, тыс. руб.
|
|
Средняя
зара-ботная плата, руб
|
Средняя числен-ность работ-ников, чел.
|
Средняя
зара-ботная плата, руб
|
Средняя
числен-ность работ-ников, чел.
|
Базисный период
|
Отчетный период
|
Отчетный по срав-нению с базисным
|
|
З0
|
Ч0
|
З1
|
Ч1
|
З0 Ч0
|
З1 Ч1
|
З0 Ч1
|
|
1
|
2
|
3
|
4
|
5=7÷4
|
6=2*3
|
7
|
8=2*5
|
|
1
|
5000
|
100
|
6500
|
105
|
500
|
682,5
|
525
|
|
2
|
5600
|
100
|
8000
|
95
|
560
|
760,0
|
532
|
|
Итого
|
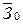 =5300 =5300
|
200
|
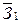 =7212,5 =7212,5
|
200
|
1060
|
1442,5
|
1057
|
Величина фонда заработной платы в отчетном периоде (графа 7 табл. 19)
дана в условии задания 4 (табл. 17). Среднесписочная численность работников в
отчетном периоде (графа 5) и фонд заработной платы в базисном периоде (графа 6)
вычисляются, исходя из формулы (21).
Используя
полученные данные (табл. 19), вычисляем индекс средней заработной платы
переменного состава по формуле (23):
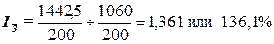 ;
;
индекс средней заработной платы
постоянного состава по формуле (24):
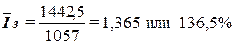 ;
;
индекс средней заработной платы структурных сдвигов по формуле (25):
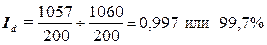 .
.
Проверка полученных результатов
осуществляется по формуле (26):
1,361 = 1,365 · 0,997
1,361 = 1,361 (верное равенство).
Изменением
доли каждой организации с разным уровнем средней заработной платы в общем фонде
заработной платы проиллюстрировано в таблице 20.
Таблица 20
Доля организаций с разным уровнем средней заработной
платы в общем фонде заработной платы.
|
№ орга-низа-ции п/п
|
Средняя численность работников, чел
|
Доля организаций
|
|
Базисный
период
|
Отчетный период
|
Базисный период
|
Отчетный период
|
|
Ч0
|
Ч1
|
d0
|
d1
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
100
|
105
|
0.5
|
0.525
|
|
2
|
100
|
95
|
0.5
|
0.475
|
|
Итого
|
200
|
200
|
1
|
1
|
Вывод: Средняя заработная плата по двум
организациям вместе в отчетном периоде по сравнению с базисным выросла на 36,1
% (в то время как по данным таблицы 18 в 1-ой организации она увеличилась на
30%, а во 2-ой – на 43%). Такое изменение средней заработной платы по двум
организациям вместе объясняется изменением средней заработной платы в каждой
организации и изменением доли организации с разным уровнем средней заработной
платы в общем фонде заработной платы. Так, в результате изменения средней
заработной платы в каждой из организаций (без учета структурных сдвигов) средняя
заработная плата по двум организациям вместе выросла на 36,5 %. В результате же
того, что в общем фонде заработной платы увеличилась доля 1-ой организации с
более низким уровнем средней заработной платы (табл. 20), средняя заработная
плата по двум организациям вместе, наоборот, снизилась на 0,3 %. Следует
отметить, что столь небольшое изменение средней заработной платы по двум
организациям в результате структурных сдвигов объясняется лишь незначительным
изменением доля организаций с разным уровнем средней заработной платы в общем
фонде заработной платы изменилась (на 2,5%).
2.2 Определение абсолютного изменения
средней заработной платы в целом и за счет отдельных факторов
Абсолютное
изменение средней заработной платы в целом, под влиянием двух факторов
(изменением средней заработной платы в каждой организации и изменением доли
организаций с различной среднесписочной численностью работников) определяется
по формуле:
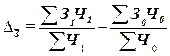 . (27)
. (27)
Абсолютное
изменение средней заработной платы в результате изменения средней заработной
платы в каждой организации рассчитывается по формуле:
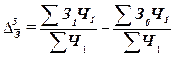 . (28)
. (28)
Абсолютное
изменение средней заработной платы в результате изменения среднесписочной
численности работников в каждой организации определяется по формуле:
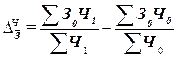 . (29)
. (29)
Между
абсолютными значениями средней заработной платы в целом и за счет отдельных
факторов существует взаимосвязь:
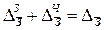 .
(30)
.
(30)
Используя данные,
полученные ранее (табл. 19), можно определить абсолютные изменение средней
заработной платы в целом и за счет отдельных факторов:
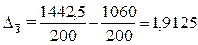 тыс. руб. = 1912,5
руб.,
тыс. руб. = 1912,5
руб.,
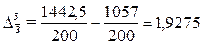 тыс. руб. = 1927,5 руб.,
тыс. руб. = 1927,5 руб.,
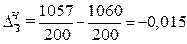 тыс. руб. = - 15 руб.
тыс. руб. = - 15 руб.
Проверка полученных результатов
осуществляется по формуле (30):
1912,5 =
1927,5 - 15,
1912,5 = 1912,5
(верное равенство).
Вывод. Средняя заработная плата по двум
организациям вместе в отчетном периоде по сравнению с базисным выросла на
1912,5 руб. (в то время как по данным таблицы 18 в 1-ой организации она
увеличилась на 1500 руб., а во 2-ой – на 2400 руб. Причем, за счет изменения средней
заработной платы в каждой из организаций (без учета структурных сдвигов) средняя
заработная плата по двум организациям вместе выросла на 1927,5 руб. А в
результате того, что в общем фонде заработной платы увеличилась доля 1-ой
организации (на 2,5%) с более низким уровнем средней заработной платы, средняя
заработная плата по двум организациям вместе, наоборот, снизилась на 15 руб.
2.2 Определение
абсолютного изменения фонда заработной платы вследствие изменения среднесписочной
численности работников, средней заработной платы и двух факторов вместе
Абсолютное
изменение фонда заработной платы в целом, под влиянием двух факторов
(изменением средней заработной платы и среднесписочной численности работников)
определяется по формуле:
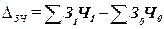 . (31)
. (31)
Абсолютное
изменение фонда заработной платы в результате изменения средней заработной
платы в каждой организации рассчитывается по формуле:
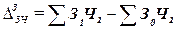 . (32)
. (32)
Абсолютное
изменение средней заработной платы в результате изменения среднесписочной
численности работников в каждой организации определяется по формуле:
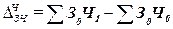 . (33)
. (33)
Между абсолютными
значениями средней заработной платы в целом и за счет отдельных факторов
существует взаимосвязь:
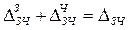 . (34)
. (34)
Расчет
абсолютных изменений фонда заработной платы в целом и за счет отдельных
факторов по формулам (31) – (33):
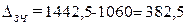 тыс. руб.,
тыс. руб.,
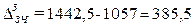 тыс. руб.,
тыс. руб.,
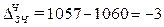 тыс. руб.
тыс. руб.
Проверка полученных результатов
осуществляется по формуле (30):
382,5 = 385,5
- 3,
382,5 = 382,5
(верное равенство).
Вывод. Общий фонд заработной платы (для двух
организаций вместе) увеличился на 382,5 тыс. руб., что является следствием
действия двух факторов – увеличения средней заработной платы (что привело к
росту фонда заработной платы на 385,2 тыс. руб.) и увеличения среднесписочной
численности работников (что привело к снижению фонда заработной платы на 3 тыс.
руб.).
Литература
1.
Громыко Г.Л. Теория статистики: Учебник. - М.:
ИНФРА-М, 2006.
2.
Громыко Г.Л. Теория статистики: Практикум. - М.:
ИНФРА-М, 2003.
3. Гусаров В.М. Статистика: Учеб.
пособие для вузов. - М.: ЮНИТИ - ДАНА, 2001.
4.
Гусаров
В.М. Статистика: Учеб пособие/ В.М. Гусаров, Е.И. Кузнецова. – 2-е изд.,
перераб. и доп. – М.: ЮНИТИ-ДАНА, 2007.
5. Общая теория статистики:
Статистическая методология в изучении коммерческой деятельности: Учебник / Под.
ред. Башиной О.Э., Спирина А.А. – М.: Финансы и статисика, 2005.
6. Практикум по статистике: Учеб.
пособие для вузов/ Под ред. В.М. Симчеры. - М.: Финстатинформ, 1999.
7. Практикум по теории статистики:
Учебное пособие/Под. ред. Шмойловой Р.А. – М.: Финансы и статистика, 2004.
8. Сироткина Т.С., Каманина А.М. Основы
теории статистики: Учеб. пособие для вузов/ Под ред. проф. В.М. Симчеры. - М.:
Финстатинформ, 1995, 1996.
9. Статистика: Учеб. пособие/А.В. Багат,
М.М. Конкина, В.М. Симчера и др.; Под ред. В.М. Симчеры.- М.: Финансы и
статистика, 2005.
10. Теория статистики: Учебник/Под. ред.
Шмойловой Р.А. – М.: Финансы и статистика, 2001; 2003; 2006.