Содержание
Введение. 2
1. 1.
История зарождения ЭВМ.. 3
Машина
Паскаля. 3
Аналитическая
машина Беббиджа. 3
Разработка
первого компьютера. 4
Электронный
калькулятор. 5
2. Принципы
фон Неймана, как предпосылки создания
компьютера. 6
3. Реализация
принципа фон Неймана в конструкции современных персональных компьютеров. 7
4. Принципы
работы компьютера с программой. 8
5. Арифметические
основы работы компьютера. Кодирование чисел и символов системы.. 10
6. Исчисление
компьютера, двоичные и шестнадцатеричные системы. Арифметические операции,
таблицы кодирования символов. 14
7. Заключение. 25
Список используемой литературы.. 26
Введение
Самая фундаментальная
отличительная черта информации в будущем - почти вся она станет цифровой. Уже
сейчас во многих библиотеках печатные материалы сканируют и хранят как
электронные данные на обычных или на компакт-дисках. Газеты и журналы теперь
зачастую готовят в электронной форме, а печатают на бумаге только для
распространения. Электронную информацию можно хранить вечно - или столько,
сколько нужно - в компьютерных базах данных. С каждым годом совершенствуются
методы сбора информации и превращения ее в квадрильоны крошечных пакетов
данных. Как только цифровая информация помещается в то или иное
"хранилище", любой, у кого есть персональный компьютер и средства
доступа к базам данных, может мгновенно обратиться к ней и использовать ее по
своему усмотрению.
1. 1. История зарождения ЭВМ
Машина Паскаля
Идея применять для
манипуляций с числами какой-нибудь инструмент не нова. До 1642 года, когда
девятнадцатилетний французский ученый Блез Паскаль изобрел механическое счетное
устройство - суммирующую машину, в Азии уже почти 5000 лет пользовались
счетами. Три десятилетия спустя немецкий математик Готфрид Лейбниц
усовершенствовал конструкцию машины Паскаля. Его "шаговый
вычислитель" позволял умножать, делить и вычислять квадратные корни.
Весьма надежные механические арифмометры, напичканные шестеренками и наборными
счетчиками, наследники шагового вычислителя, служили главной опорой бизнесу
вплоть до их замены электронными аналогами.
Аналитическая машина Беббиджа
Более полутора столетий назад видного
британского математика озарила гениальная идея, которая прославила его имя уже
при жизни. Чарлз Беббидж, профессор математики Кембриджского университета,
понял, что можно построить механическое устройство, способное выполнять
последовательность взаимосвязанных вычислений, - своего рода компьютер! Где-то
в начале тридцатых годов прошлого столетия он пришел к выводу, что машина
сможет манипулировать информацией, если только ту удастся преобразовать в
числа. Беббидж видел машину, приводимую в действие паром, состоящую из штифтов,
зубчатых колес, цилиндров и других механических частей - в общем, настоящее
детище начинавшегося тогда индустриального века. По мысли Беббиджа,
"аналитическая машина" должна была избавить человечество от
монотонных вычислений и ошибок, с ними связанных.
Аналитическая машина
задумывалась как механическая, но ученый предвидел, что она сможет следовать
варьируемым наборам инструкций и тем самым служить разным целям. В том же и
смысл программного обеспечения. Современная программа - это внушительный набор
правил, посредством которых машину "инструктируют", как решать ту или
иную задачу. Беббидж понимал, что для ввода таких инструкций нужен совершенно
новый тип языка, и он изобрел его, использовав цифры, буквы, стрелки и другие
символы. Этот язык позволил бы "программировать" аналитическую машину
длинными сериями условных инструкций, что, в свою очередь, позволило бы машине
реагировать на изменение ситуации. Он - первый, кто увидел, что одна машина
способна выполнять разные функции.
Разработка первого компьютера
Следующее столетие ученые
математики работали над идеями, высказанными Беббиджем, и к середине сороковых
годов нашего века электронный компьютер, наконец, был построен - на основе
принципов аналитической машины. Создателей современного компьютера выделить
трудно, поскольку все исследования проводились во время второй мировой войны
под покровом полной секретности, главным образом - в Соединенных Штатах и
Великобритании. Основной вклад внесли три человека: Алан Тьюринг, Клод
Шеннон и Джон фон Нейман.
В середине тридцатых
годов Алан Тьюринг - блестящий британский математик, как и Беббидж, получивший
образование в Кембридже, предложил свой вариант универсальной вычислительной
машины, которая могла бы в зависимости от конкретных инструкций работать
практически с любым видом информации. Сегодня она известна как машина Тьюринга.
А в конце тридцатых Клод
Шеннон, тогда еще студент, доказал, что машина, исполняющая логические
инструкции, может манипулировать информацией. В своей магистерской диссертации
он рассмотрел, как с помощью электрических цепей компьютера выполнять
логические операции, где единица - "истина" (цепь замкнута), а нуль -
"ложь" (цепь разомкнута).
Здесь речь идет о
двоичной системе счисления, иначе говоря, о коде. Двоичная система - это азбука
электронных компьютеров, основа языка, на который переводится и с помощью
которого хранится и используется вся информация в компьютере.
Электронный калькулятор
Двоичное представление
чисел позволяет создавать калькуляторы, пользуясь преимуществами электрических
цепей. Именно так и поступила во время второй мировой войны группа
математиков при Пенсильванском
университете, возглавляемая Дж. Преспером Эккертом и Джоном Моучли, начав
разработку электронно-вычислительной машины - электронный числовой интегратор и
калькулятор. Перед учеными поставили цель - ускорить расчеты таблиц для
наведения артиллерии. ENIAC больше походил на электронный калькулятор, чем на
компьютер, но двоичные числа представляли уже не примитивными колесиками, как в
арифмометрах, а электронными лампами - "переключателями".
ENIAC весил 30 тонн и
занимал большое помещение. "Вычислительные" импульсы бегали в нем по
1500 электромеханическим реле и 17000 электронным лампам. Он потреблял 150000
ватт электроэнергии и при этом хранил объем информации, эквивалентный всего
лишь 80 символам.
Основной недостаток этой
машины - стоило перегореть хотя бы одной лампе, как ENIAC тут же вставал, а когда
все лампы работали, инженерный персонал мог настроить ENIAC на какую-нибудь
задачу, вручную изменив подключения 6000 проводов. Все эти провода приходилось
вновь переключать, когда вставала другая задача. В решении этой проблемы
основную заслугу приписывают Джону фон Нейману. Он придумал схему, которой до
сих пор следуют все цифровые компьютеры. "Архитектура фон Неймана",
как ее теперь называют, базируется на принципах, сформулированных им в 1945
году. В их число входит и такой: в компьютере не придется изменять подключения
проводов, если все инструкции будут храниться в его памяти. И как только эту
идею воплотили на практике, родился современный компьютер.
2. Принципы фон Неймана, как предпосылки
создания компьютера
В основу построения подавляющего
большинства ЭВМ положены следующие общие принципы, сформулированные в 1945 году
американским ученым венгерского происхождения Джоном фон Нейманом.
Прежде всего, компьютер должен иметь
следующие устройства:
1. Арифметическо-логическое устройство,
выполняющие арифметические и логические операции;
2. Устройство управления, которое
организует процесс выполнения программ;
3. Запоминающее устройство, или память
для хранения программ и данных;
4. Внешние устройства для ввода-вывода
информации.
В основе работы компьютера лежат
следующие принципы:
1 Принцип двоичного кодирования.
Согласно этому принципу, вся информация, поступающая в ЭВМ, кодируется с
помощью двоичных сигналов.
2 Принцип программного управления. Из
него следует, что программа состоит из набора команд, которые выполняются
процессором автоматически друг за другом в определенной последовательности.
3 Принцип однородности памяти.
Программы и данные хранятся в одной и той же памяти. Поэтому ЭВМ не различает,
что хранится в данной ячейке памяти - число, текст или команда. Над командами
можно выполнять такие же действия, как и над данными.
4 Принцип адресности. Структурно
основная память состоит из пронумерованных ячеек; процессору в произвольный
момент времени доступна любая ячейка.
Машины, построенные на этих
принципах, называются Фон-Неймановскими.
3.
Реализация принципа фон Неймана в
конструкции современных персональных компьютеров.
Более чем за полвека развития вычислительных
средств прогресс в аппаратной реализации ЭВМ и их технических характеристик
превзошел все прогнозы, и пока не заметно снижение его темпов. Несмотря на то,
что современные компьютеры не имеют ничего общего с первыми моделями,
основополагающе идеи, заложенные в них и связанные с понятием алгоритма,
разработанным Аланом Тьюрингом, а также архитектурной реализацией, предложенной
Джоном фон Нейманом, пока не претерпели коренных изменений (за исключением
систем параллельной обработки информации). В связи с этим закономерно в
качестве блок-схемы привести следующую логическую структуру:
|
|
|
Процессор
|
|
|
|
|
|
|
АЛУ
|
|
|
|
|
УВВ
|
|
системный
|
интерфейс
|
|
ЗУ
|
|
|
|
|
|
|
|
|
|
|
|
УУ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ПУ
|
|
·
АЛУ – арифметико-логическое устройство;
·
УУ – устройство управления;
·
ЗУ – запоминающее устройство;
·
УВВ – устройство ввода-вывода;
·
ПУ – пульт управления.
4. Принципы работы компьютера с программой.
Процессор, или микропроцессор, является основным
устройством ПК. Он предназначен для выполнения вычислений по хранящейся в
запоминающем устройстве программе и обеспечения общего управления ПК.
Быстродействие ПК в значительной мере определяется скоростью работы процессора.
Для ее увеличения процессор использует собственную память небольшого объема,
именуемую местной или сверхоперативной, что в некоторых случаях исключает
необходимость обращения к запоминающему устройству ПК.
Вычислительный процесс должен быть предварительно
представлен для ПК в виде программы – последовательности инструкций (команд),
записанных в порядке выполнения. В процессе выполнения программы ПК выбирает
очередную команду, расшифровывает ее, определяет, какие действия и над какими
операндами следует выполнить. Эту функцию осуществляет УУ. Оно же помещает
выбранные из ЗУ операнды в АЛУ, где они и обрабатываются. Само АЛУ работает под
управлением УУ.
Обрабатываемые данные и выполняемая программа
должны находиться в запоминающем устройстве – памяти, куда они вводятся через
устройство ввода. Емкость памяти измеряется в величинах, кратных байту. Память
представляет собой сложную структуру, построенную по иерархическому принципу, и
включает в себя запоминающие устройства различных типов. Функционально она
делится на две части: внутреннюю и внешнюю.
Внутренняя, или основная память – это запоминающее
устройство, напрямую вязанное с процессором и предназначенное для хранения
выполняемых программ и данных, непосредственно участвующих в вычислениях.
Обращение к внутренней памяти ПК осуществляется с высоким быстродействием, но
она имеет ограниченный объем, определяемый системой адресации машины.
Внутренняя память, в свою очередь, делится на
оперативную (ОЗУ) и постоянную (ПЗУ) память. Оперативная память, по объему
составляющая большую часть внутренней памяти, служит для приема, хранения и
выдачи информации. При выключении питания ПК содержимое оперативной памяти в
большинстве случаев теряется. Постоянная память обеспечивает хранение и выдачу
информации. В отличие от содержимого оперативной памяти, содержимое постоянной
заполняется при изготовлении ПК и не может быть изменено в обычных условиях
эксплуатации. В постоянной памяти хранятся часто используемые (универсальные)
программы, и данные, к примеру, некоторые программы операционной системы,
программы тестирования оборудования ПК и др. при выключении питания содержимое
постоянной памяти сохраняется.
Внешняя память (ВЗУ) предназначена для размещения
больших объемов информации и обмена ею с оперативной памятью. Для построения
внешней памяти используют энергонезависимые носители информации (диски и
ленты), которые к тому же являются переносимыми. Емкость этой памяти
практически не имеет ограничений, а для обращения к ней требуется больше
времени, чем ко внутренней.
Внешние запоминающие устройства конструктивно
отделены от центральных устройств ПК (процессора и внутренней памяти), имеют
собственное управление и выполняют запросы процессора без его непосредственного
вмешательства. В качестве ВЗУ используют накопители на магнитных и оптических
дисках, а также накопители на магнитных лентах.
ВЗУ по принципам функционирования разделяются на
устройства прямого доступа (накопители на магнитных и оптических дисках) и
устройства последовательного доступа (накопители на магнитных лентах).
Устройства прямого доступа обладают большим быстродействием, поэтому они
являются основными внешними запоминающими устройствами, постоянно используемыми
в процессе функционирования ПК. Устройства последовательного доступа
используются в основном для резервирования информации.
Устройства ввода-вывода служат соответственно для
ввода информации в ПК и вывода из нее, а также для обеспечения общения
пользователя с машиной. Процессы ввода-вывода протекают с использованием
внутренней памяти ПК. Иногда устройства ввода-вывода называют периферийными или
внешними устройствам ПК. К ним относятся, в частности, дисплеи (мониторы),
клавиатура, манипуляторы типа «мышь», алфавитно-цифровые печатающие устройства
(принтеры), графопостроители, сканеры и др. для управления внешними
устройствами (в том числе и ВЗУ) и согласования их с системным интерфейсом
служат групповые устройства управления внешними устройствами, адаптеры или
контроллеры.
Пульт управления служит для выполнения оператором
или системным программистом системных операций в ходе управления вычислительным
процессом.
5.
Арифметические основы работы
компьютера. Кодирование чисел и символов системы
Современные ЭВМ имеют достаточно развитую систему команд,
включающую десятки и сотни машинных операций. Однако выполнение любой операции
основано на использовании простейших микроопераций типа сложения и сдвиг. Это
позволяет иметь единое арифметико-логическое устройство для выполнения любых
операций, связанных с обработкой информации. Правила сложения двоичных цифр
двух чисел А и В представлены в табл.1.[1]
Здесь показаны правила сложения двоичных цифр ai, bi
одноименных разрядов с учетом возможных переносов из предыдущего разряда pi-1.
Подобные таблицы можно было бы построить для любой
другой арифметической и логической операции (вычитание, умножение и т.д.), но
именно данные этой таблицы положены в основу выполнения любой операции ЭВМ. Под
знак чисел отводится специальный знаковый разряд. Знак ⌠+ кодируется
двоичным нулем, а знак ⌠- - единицей. Действия над прямыми кодами двоичных
чисел при выполнении операций создают большие трудности, связанные с
необходимостью учета значений знаковых разрядов:
Таблица 1
Правила сложения двоичных цифр
|
Значения
двоичных
чисел
А и В
|
Разряд
Суммы
Si
|
Перенос
в следующий разряд
Рi
|
|
аi
|
bi
|
Pi-1
|
|
0
0
0
0
1
1
1
1
|
0
0
1
1
0
0
1
1
|
0
1
0
1
0
1
0
1
|
0
1
1
0
1
0
0
1
|
0
0
0
1
0
1
1
1
|
-
во-первых, следует отдельно обрабатывать значащие разряды
чисел и разряды знака;
-
во-вторых, значение разряда знака влияет на алгоритм
выполнения операции (сложение может заменяться вычитанием и наоборот).
Во всех ЭВМ без исключения все операции выполняются
над числами, представленными специальными машинными кодами. Их использование позволяет
обрабатывать знаковые разряды чисел так же, как и значащие разряды, а также
заменять операцию вычитания операцией сложения.
Различают прямой код (П), обратный код (ОК) и
дополнительный код (ДК) двоичных чисел.
Прямой код двоичного числа образуется из абсолютного
значения этого числа и кода знака (нуль или единица) перед его старшим числовым
разрядом.
Пример 1.
A10=+10 A2=+1010 [A2]П=0:1010;
B10=-15 B2=-1111 [B2]П=1:1111.
Точечной вертикальной линией здесь отмечена условная
граница, отделяющая знаковый разряд от значащих.
Обратный код двоичного числа образуется по следующему
правилу. Обратный код положительных чисел совпадает с их прямым кодом. Обратный
код отрицательного числа содержит единицу в знаковом разряде числа, а значащие
разряды числа заменяются на инверсные, т.е. нули заменяются единицами, а
единицы - нулями.[2]
Пример 2.
A10=+5 A2=+101 [A2]П=[A2]OK=0:101;
B10=-13 B2=-1010 [B2]OK=1:0010.
Свое название обратный код чисел получил потому, что
коды цифр отрицательного числа заменены на инверсные. Укажем наиболее важные
свойства обратного кода чисел:
∙ сложение положительного числа С с его
отрицательным значением в обратном коде дает так называемую машинную единицу
МЕок= 1: 111... 11, состоящую из единиц в знаковом и значащих разрядах числа;
∙ нуль в обратном коде имеет двоякое значение.
Он может быть положительным - 0: 00...0 и отрицательным числом - 1; 11... 11.
Значение отрицательного нуля совпадает с МЕок. Двойственное представление нуля
явилось причиной того, что в современных ЭВМ все числа представляются не
обратным, а дополнительным кодом. Дополнительный код положительных чисел совпадает
с их прямым кодом. Дополнительный код отрицательного числа представляет собой
результат суммирования обратного кода числа с единицей младшего разряда
(2° - для целых чисел, 2-k - для дробных).
Укажем основные свойства дополнительного кода:
сложение дополнительных кодов положительного числа С с его отрицательным значением
дает так называемую машинную единицу дополнительного кода:
МЕДК=МЕОК+20=10:
00┘00,
т.е. число 10 (два) в знаковых разрядах числа;
дополнительный код получил такое свое название потому,
что представление отрицательных чисел является дополнением прямого кода чисел
до машинной единицы МЕдк.
Модифицированные обратные и дополнительные коды
двоичных чисел отличаются соответственно от обратных и дополнительных кодов
удвоением значений знаковых разрядов. Знак ⌠+ в этих кодах кодируется
двумя нулевыми знаковыми разрядами, а ⌠- - двумя единичными разрядами.
Целью введения модифицированных кодов являются
фиксация и обнаружение случаев получения неправильного результата, когда значение
результата превышает максимально возможный результат в отведенной разрядной
сетке машины. В этом случае перенос из значащего разряда может исказить значение
младшего знакового разряда. Значение знаковых разрядов ⌠01
свидетельствует о положительном переполнении разрядной сетки, а ⌠10 - об
отрицательном переполнении. В настоящее время практически во всех моделях ЭВМ
роль удвоенных разрядов для фиксации переполнения разрядной сетки играют переносы,
идущие в знаковый и из знакового разряда.
6.
Исчисление компьютера, двоичные и
шестнадцатеричные системы. Арифметические операции, таблицы кодирования
символов.
В
повседневной практике для представления чисел люди пользуются почти
исключительно десятичной системой счисления. Лишь в редких случаях встречаются
остатки других систем - римский счет, двенадцатеричная система (часы),
шестидесятеричная (минуты).
Однако
система изображения чисел, которая веками складывалась применительно к ручному
труду, не позволяет получить наиболее эффективные методы выполнения вычислений.
По этой причине в вычислительной технике применяются другие системы счисления и
чаще всего - двоичная. Введем несколько определений.
Cистема
счисления -
совокупность символов и правил для обозначения чисел.
Разделяют
системы счисления позиционные и непозиционные. Непозиционная система счисления
задается перечислением изображаемых в ней значений. Позиционная система
счисления характеризуется основанием и тем, что числа, как правило,
представляются несколькими разрядами (являются многоразрядными), а вес любого
разряда определяется его позицией в числе.
Oснование позиционной системы счисления
определяет количество различных цифр (символов), допустимое в системе
счисления. Это же число определяет, во сколько раз вес цифры данного разряда
меньше веса цифры соседнего старшего разряда.
Так, в
десятичной системе счисления, основание которой равно 10, различают 10 арабских
цифр - 0, 1, 2, ..., 9. Следовательно, при ее использовании для записи числа,
не превышающего девяти, достаточно одной цифры, и такое число записывается как
одноразрядное. А в случае записи числа, большего девяти, оно представляется как
многоразрядное. При этом вес каждого более старшего (расположенного слева от
текущего) разряда в десять (основание системы счисления) раз больше текущего.
В вычислительной технике
широко применяют двоичную, восьмеричную и шестнадцатиричную систему счисления.
Двоичная
система счисления имеет основание 2, и, следовательно, две разных цифры - 0 и
1; восьмеричная - восемь разных цифр - 0, 1, 2, 3, 4, 5, 6, 7, а
шестнадцатеричная - шестнадцать цифр - десять арабских цифр от 0 до 9 и еще
шесть символов -
А (цифра,
изображающая десять), D (цифра тринадцать),
В (цифра
одиннадцать), E (цифра четырнадцать),
С (цифра
двенадцать), F (цифра пятнадцать).
Проще всего
сопоставить запись одних и тех же чисел в этих системах счисления можно с
использованием таблицы 1, приведенной на следующей странице.
Мы уже
говорили о том, что современные цифровые ЭВМ все используют в качестве основной
двоичную систему счисления. К ее достоинствам относится:
·
простота
выполнения арифметических и логических операций, что влечет за собой простоту
устройств, реализующих эти операции;
·
возможность
использования аппарата алгебры логики (булевой алгебры) для анализа и синтеза
операционных устройств ЭВМ.
К неудобствам
двоичной системы счисления относится необходимость перевода чисел из десятичной
в двоичную и наоборот, а также то, что запись числа в двоичной системе
громоздка (требует большего числа разрядов, чем привычная для человека
десятичная). По этой и ряду других причин, кроме двоичной применяются восьмеричная
и шестнадцатеричная системы счисления.
Система счисления - это совокупность правил и приемов
записи чисел с помощью набора цифровых знаков. Количество цифр, необходимых для
записи числа в системе, называют основанием системы счисления. Основание системы
записывается в справа числа в нижнем индексе:
; 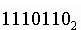 ;
; 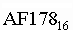
и т. д.
Различают два типа систем счисления:
-
позиционные, когда значение каждой цифры числа определяется
ее позицией в записи числа;
-
непозиционные, когда значение цифры в числе не зависит от ее
места в записи числа.
Примером непозиционной системы счисления является
римская: числа IX, IV, XV и т.д. Примером позиционной системы счисления является
десятичная система, используемая повседневно.
Любое целое число в позиционной системе можно записать
в форме многочлена:
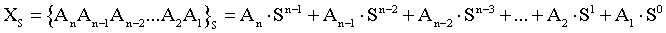
где S - основание системы счисления;
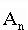 - цифры
числа, записанного в данной системе счисления;
- цифры
числа, записанного в данной системе счисления;
n - количество разрядов числа.
Пример. Число 629310 запишется в форме
многочлена следующим образом:
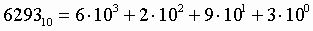
Римская система счисления является непозиционной
системой. В ней для записи чисел используются буквы латинского алфавита. При
этом буква I всегда означает единицу, буква - V пять, X - десять, L -
пятьдесят, C - сто, D - пятьсот, M - тысячу и т.д. Например, число 264
записывается в виде CCLXIV. При записи чисел в римской системе счисления
значением числа является алгебраическая сумма цифр, в него входящих. При этом
цифры в записи числа следуют, как правило, в порядке убывания их значений, и не
разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за
цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в
целом является отрицательным. Типичные примеры, иллюстрирующие общие правила
записи чисел в римской система счисления, приведены в таблице.
Таблица 2
Запись чисел в римской системе счисления
|
1
|
2
|
3
|
4
|
5
|
|
I
|
II
|
III
|
IV
|
V
|
|
6
|
7
|
8
|
9
|
10
|
|
VI
|
VII
|
VIII
|
IX
|
X
|
|
11
|
13
|
18
|
19
|
22
|
|
XI
|
XIII
|
XVIII
|
XIX
|
XXII
|
|
34
|
39
|
40
|
60
|
99
|
|
XXXIV
|
XXXIX
|
XL
|
LX
|
XCIX
|
|
200
|
438
|
649
|
999
|
1207
|
|
CC
|
CDXXXVIII
|
DCXLIX
|
CMXCIX
|
MCCVII
|
|
2045
|
3555
|
3678
|
3900
|
3999
|
|
MMXLV
|
MMMDLV
|
MMMDCLXXVIII
|
MMMCM
|
MMMCMXCIX
|
Недостатком римской системы является отсутствие
формальных правил записи чисел и, соответственно, арифметических действий с
многозначными числами. По причине неудобства и большой сложности в настоящее
время римская система счисления используется там, где это действительно удобно:
в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных
бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.
Десятичная система счисления – в настоящее время
наиболее известная и используемая. Изобретение десятичной системы счисления
относится к главным достижениям человеческой мысли. Без нее вряд ли могла
существовать, а тем более возникнуть современная техника. Причина, по которой
десятичная система счисления стала общепринятой, вовсе не математическая. Люди
привыкли считать в десятичной системе счисления, потому что у них по 10 пальцев
на руках.
Древнее изображение десятичных цифр (рис) не случайно:
каждая цифра обозначает число по количеству углов в ней. Например, 0 - углов
нет, 1 - один угол, 2 - два угла и т.д. Написание десятичных цифр претерпело
существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.

Десятичная система впервые появилась в Индии примерно
в VI веке новой эры. Индийская нумерация использовала девять числовых символов
и нуль для обозначения пустой позиции. В ранних индийских рукописях, дошедших
до нас, числа записывались в обратном порядке - наиболее значимая цифра ставилась
справа. Но вскоре стало правилом располагать такую цифру с левой стороны.
Особое значение придавалось нулевому символу, который вводился для позиционной
системы обозначений. Индийская нумерация, включая нуль, дошла и до нашего
времени. В Европе индусские приёмы десятичной арифметики получили
распространение в начале ХIII в. благодаря работам итальянского математика
Леонардо Пизанского (Фибоначчи). Европейцы заимствовали индийскую систему
счисления у арабов, назвав ее арабской. Это исторически неправильное название
удерживается и поныне.
Десятичная система использует десять цифр – 0, 1, 2,
3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и
запятую или точку для разделения целой и дробной частей числа.
В вычислительных машинах используется двоичная система
счисления, её основание - число 2. Для записи чисел в этой системе используют
только две цифры - 0 и 1. Вопреки распространенному заблуждению, двоичная
система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками
и философами задолго до появления компьютеров, еще в ХVII - ХIХ веках. Первое
опубликованное обсуждение двоичной системы счисления принадлежит испанскому
священнику Хуану Карамюэлю Лобковицу (1670 г.). Всеобщее внимание к этой системе
привлекла статья немецкого математика Готфрида Вильгельма Лейбница,
опубликованная в 1703 г.
В ней пояснялись двоичные операции сложения, вычитания, умножения и деления.
Лейбниц не рекомендовал использовать эту систему для практических вычислений,
но подчёркивал её важность для теоретических исследований. Со временем двоичная
система счисления становится хорошо известной и получает развитие.
Выбор двоичной системы для применения в вычислительной
технике объясняется тем, что электронные элементы - триггеры, из которых
состоят микросхемы ЭВМ, могут находиться только в двух рабочих состояниях.
С помощью двоичной системы кодирования можно
зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип
кодирования и передачи информации с помощью азбуки Морзе. Телеграфист,
используя только два символа этой азбуки - точки и тире, может передать
практически любой текст.
Двоичная система удобна для компьютера, но неудобна
для человека: числа получаются длинными и их трудно записывать и запоминать.
Конечно, можно перевести число в десятичную систему и записывать в таком виде,
а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому
применяются системы счисления, родственные двоичной - восьмеричная и
шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8
и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные
латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу
10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих
систем объясняется тем, что переход к записи числа в любой из этих систем от
его двоичной записи очень прост. Ниже приведена таблица соответствия чисел,
записанных в разных системах.
Таблица 3
Соответствие чисел, записанных в различных системах счисления
|
Десятичная
|
Двоичная
|
Восьмеричная
|
Шестнадцатеричная
|
|
1
|
001
|
1
|
1
|
|
2
|
010
|
2
|
2
|
|
3
|
011
|
3
|
3
|
|
4
|
100
|
4
|
4
|
|
5
|
101
|
5
|
5
|
|
6
|
110
|
6
|
6
|
|
7
|
111
|
7
|
7
|
|
8
|
1000
|
10
|
8
|
|
9
|
1001
|
11
|
9
|
|
10
|
1010
|
12
|
A
|
|
11
|
1011
|
13
|
B
|
|
12
|
1100
|
14
|
C
|
|
13
|
1101
|
15
|
D
|
|
14
|
1110
|
16
|
E
|
|
15
|
1111
|
17
|
F
|
|
16
|
10000
|
20
|
10
|
Перевод
чисел из одной категории в другую
Перевод чисел из одной системы счисления в другую
составляет важную часть машинной арифметики. Рассмотрим основные правила
перевода.[3]
1. Для перевода двоичного числа в десятичное
необходимо его записать в виде многочлена, состоящего из произведений цифр
числа и соответствующей степени числа 2, и вычислить по правилам десятичной
арифметики:
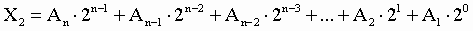
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4
Степени числа 2
|
n (степень)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
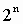
|
1
|
2
|
4
|
8
|
16
|
32
|
64
|
128
|
256
|
512
|
1024
|
2. Для перевода восьмеричного числа в десятичное
необходимо его записать в виде многочлена, состоящего из произведений цифр
числа и соответствующей степени числа 8, и вычислить по правилам десятичной
арифметики:

При переводе удобно пользоваться таблицей степеней
восьмерки:
Таблица 5
Степени числа 8
|
n (степень)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
|
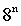
|
1
|
8
|
64
|
512
|
4096
|
32768
|
262144
|
3. Для перевода шестнадцатеричного числа в десятичное
необходимо его записать в виде многочлена, состоящего из произведений цифр
числа и соответствующей степени числа 16, и вычислить по правилам десятичной
арифметики:
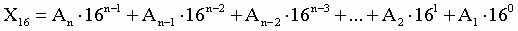
При переводе удобно пользоваться таблицей степеней
числа 16:
Таблица 6
Степени числа 16
|
n (степень)
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
|
|
1
|
16
|
256
|
4096
|
65536
|
1048576
|
16777216
|
4. Для перевода десятичного числа в двоичную систему
его необходимо последовательно делить на 2 до тех пор, пока не останется остаток,
меньший или равный 1. Число в двоичной системе записывается как последовательность
последнего результата деления и остатков от деления в обратном порядке.
5. Для перевода десятичного числа в восьмеричную
систему его необходимо последовательно делить на 8 до тех пор, пока не
останется остаток, меньший или равный 7. Число в восьмеричной системе
записывается как последовательность цифр последнего результата деления и
остатков от деления в обратном порядке.
6. Для перевода десятичного числа в шестнадцатеричную
систему его необходимо последовательно делить на 16 до тех пор, пока не
останется остаток, меньший или равный 15. Число в шестнадцатеричной системе
записывается как последовательность цифр последнего результата деления и остатков
от деления в обратном порядке.
7. Чтобы перевести число из двоичной системы в
восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего
разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду
заменить соответствующей восьмеричной цифрой (табл. 3).
8. Чтобы перевести число из двоичной системы в
шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с
младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и
каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
9. Для перевода восьмеричного числа в двоичное
необходимо каждую цифру заменить эквивалентной ей двоичной триадой.
10. Для перевода шестнадцатеричного числа в двоичное
необходимо каждую цифру заменить эквивалентной ей двоичной тетрадой.
11. При переходе из восьмеричной
системы счисления в шестнадцатеричную и обратно, необходим промежуточный
перевод чисел в двоичную систему
В вычислительных машинах
для представления информации используются цепочки байтов. Поэтому для перевода
информации из машинного представления в человеческий необходимы таблицы
кодировки символов[4] - таблицы соответствия
между символами определенного языка и кодами символов. Их еще называют кодовыми
страницами или применяют английский термин character set (который иногда
сокращают до charset).
Самой известной таблицей
кодировки является код ASCII (Американский стандартный код для обмена
информацией). Первоначально он был разработан для передачи текстов по
телеграфу, причем в то время он был 7-битовым, то есть для кодирования символов
английского языка, служебных и управляющих символов использовались только 128
7-битовых комбинаций. При этом первые 32 комбинации (кода) служили для
кодирования управляющих сигналов (начало текста, конец строки, перевод каретки,
звонок, конец текста и т.д.). При разработке первых компьютеров фирмы IBM этот
код был использован для представления символов в компьютере. Поскольку в
исходном коде ASCII было всего 128 символов, для их кодирования хватило
значений байта, у которых 8-ой бит равен 0. Значения байта с 8-ым битом, равным
1, стали использовать для представления символов псевдографики, математических
знаков и некоторых символов из языков, отличных от английского (греческого,
немецких умляутов, французских диакритических знаков и т.п.).
Когда стали
приспосабливать компьютеры для других стран и языков, места для новых символов
уже не стало хватать. Для того, чтобы полноценно поддерживать помимо
английского и другие языки, фирма IBM ввела в употребление несколько кодовых
таблиц, ориентированных на конкретные страны. Так для скандинавских стран была
предложена таблица 865 (Nordic), для арабских стран - таблица 864 (Arabic), для
Израиля - таблица 862 (Israel) и так далее. В этих таблицах часть кодов из
второй половины кодовой таблицы использовалась для представления символов
национальных а лфавитов (за счет исключения некоторых символов псевдографики).
С русским языком ситуация
развивалась особым образом. Очевидно, что замену символов во второй половине
кодовой таблицы можно произвести разными способами. Вот и появились для
русского языка несколько разных таблиц кодировки символов кириллицы: KOI8-R,
IBM-866, CP-1251, ISO-8551-5. Все они одинаково изображают символы первой
половины таблицы (от 0 до 127) и различаются представлением символов русского
алфавита и псевдографики.
Для таких же языков, как
китайский или японский, вообще 256 символов недостаточно. Кроме того, всегда
существует проблема вывода или сохранения в одном файле одновременно текстов на
разных языках (например, при цитировании). Поэтому была разработана
универсальная кодовая таблица UNICODE, содержащая символы, применяемые в языках
всех народов мира, а также различные служебные и вспомогательные символы (знаки
препинания, математические и технические символы, стрелки, диакритические знаки
и т.д.). Очевидно, что одного байта недостаточно для кодирования такого
большого множества символов. Поэтому в UNICODE используются 16-битовые
(2-байтовые) коды, что позволяет представить 65 536 символов. К настоящему
времени задействовано около 49 000 кодов (последнее значительное изменение -
введение символа валюты EURO в сентябре 1998 г.).
Для совместимости с
предыдущими кодировками первые 256 кодов совпадают со стандартом ASCII.
При создании своих первых
персональных компьютеров фирма IBM приняла в качестве своего рабочего стандарта
кодирования символьной информации таблицу ASCII. ASCII - это Американский
стандартный код для обмена информацией. Он был разработан для использования в
телеграфии задолго до появления персональных компьютеров. Строго говоря, только
первые 128 символов являются настоящими символами ASCII. Фирма IBM приняла
кодировку ASCII, расширенную до 256 позиций, задающих 8-битовый код. Этот
стандарт, именуемый кодовой таблицей 437 (USA code page), и стал стандартом
де-факто в силу того, что компьютеры IBM заняли большую часть рынка.
Программисты обычно говорят о кодах ASCII, чтобы отличить их от других чисел.
Например, "ASCII 8" относится к клавише, в то время как "8"
- это цифра, которой соответствует ASCII 56.
256 кодов ASCII позволяют
задать двоичные эквиваленты для кодирования букв английского алфавита (строчные
и прописные буквы), цифр от 0 до 9, знаков препинания и знаков математических
операций, а также некоторых управляющих сигналов (символов).
7.
Заключение
Принципы разработанные в
середине двадцатого века перевернули современную жизнь и современные компьютеры
спроектированные по принципам архитектуры Фон Неймана (Von Neumann architecture)
обрабатывают данные последовательно, одну инструкцию за цикл
Хотя сегодня развитие
компьютерной сферы шагает семимильными шагами. И разработан новый принцип
построения компьютера, основанный на параллельности вычислительных операций.
Список используемой литературы
.
1. А.А. Козырев. Самоучитель работы на
персональном компьютере. Издание четвертое переработанное и дополненное.
Издательство Михайлова В.А. Санкт-Петербург, 2004 г.
2. А.Г. Гейн, А.И. Сенокосов, Н.А.
Юнерман. Информатика. Учебник для 10 – 11 классов общеобразовательных
учреждений. Москва, «Просвещение», 2003 г.
3. Багриновский К.А., Хрусталев Е.Ю.
Новые информационные технологии. - М.: “ЭКО”. 2004.
4. Белинов С.В., Зайцев А.А. Современные
информационные технологии. – М.: Инфра-М, 2003.
5. В.П. Леонтьев. Новейшая энциклопедия
персонального компьютера 2003. – М. ОЛМА-ПРЕСС, 2003.
6. Жаров А. Железо IBM 2004
Москва: «МикроАрт», 368 с.
7. Иванченко Н.М. Компьютерные методы
обработки информации: УМК. – СПб.: Питер, 2004.
8. Каpатыгин С.Н. Информационные технологии в коммерческой
деятельности. - М.: ABF, 2004.
9. Майоров С.И. Информационные технологии. - М.: Информатика, 2003.
10.
Макарова
Н. В., Матвеева Л. А., Бройдо В. Л. Информатика: Учебник. - М.: Финансы и статистика, 2004.
11.
Толковый
словарь по вычислительным системам. Под редакцией В. Иллингуорта, Э.Л.
Глейзера, И.К. Пайла. Перевод с английского А.К. Белоцкого, Ю.А. Плахтия, А.П.
Семенова. Под редакцией кандидата технических наук Е.К. Масловского. Москва,
«Машиностроение», 2000 г.
12.
Шафрин
Ю. А. Основы компьютерной технологии. - М.: АБФ, 2005.
[1] Белинов С.В., Зайцев А.А.
Современные информационные технологии. – М.: Инфра-М, 2003. – с. 59.
[2] Багриновский К.А.,
Хрусталев Е.Ю. Новые информационные технологии. - М.: “ЭКО”. 2004. – с. 69.
[3] Иванченко Н.М.
Компьютерные методы обработки информации: УМК. – СПб.: Питер, 2004. – с. 137.
[4] А.А. Козырев. Самоучитель работы на персональном
компьютере. Издание четвертое переработанное и дополненное. Издательство
Михайлова В.А. Санкт-Петербург, 2004
г. стр. 120.