ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Контрольная работа
По курсу:
«Эконометрика»
Вариант №_5__
Уфа 2008 г
Задача 1
По предприятиям легкой
промышленности региона получена информация, характеризующая зависимость объема
выпуска продукции (Y, млн.руб.) от объема капиталовложений (Х, млн.руб.)
|
Y
|
31
|
23
|
38
|
47
|
46
|
49
|
20
|
32
|
46
|
24
|
|
Х
|
38
|
26
|
40
|
45
|
51
|
49
|
34
|
35
|
42
|
24
|
Требуется:
1. Найти параметры уравнения линейной
регрессии, дать экономическую
интерпретацию коэффициента регрессии.
2. Вычислить остатки; найти остаточную
сумму квадратов; оценить дисперсию остатков 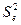 ; построить график остатков.
; построить график остатков.
3. Проверить выполнение предпосылок МНК.
4. Осуществить проверку значимости
параметров уравнения регрессии с помощью t-критерия Стьюдента (α=0,05).
5. Вычислить коэффициент детерминации,
проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05), найти
среднюю относительную ошибку аппроксимации. Сделать вывод о качестве.
6. Осуществить прогнозирование среднего значения показателя Y
при уровне значимости α=0,01 при Х=80% от его максимального
значения.
7. Представить графически фактических и
модельных значений Y, точки прогноза.
8. Составить уравнения нелинейной
регрессии:
·
Гиперболической;
·
Степенной;
·
Показательной.
Привести графики построенных уравнений регрессии.
9. Для указанных моделей
найти коэффициенты детерминации, коэффициенты
эластичности и средние относительные ошибки аппроксимации. Сравнить модели по
этим характеристикам. Сделать вывод.
Решение
1. Параметры уравнения линейной регрессии.
Уравнение линейной регрессии имеет вид:  =a+b x.
=a+b x.
Значения параметров a и b линейной модели определим, используя
данные таблицы 1.
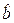 =
= 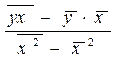 =
= 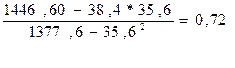
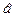 =
= 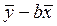 = 38,4-0,72*35,6=12,71.
= 38,4-0,72*35,6=12,71.  =12,71+0,72* x.
=12,71+0,72* x.
Таким образом, с
увеличением объема капиталовложений на 1 млн. руб. объем выпуска продукции увеличится
на 0,72млн.руб.
2. Вычисление остатков,
остаточной суммы квадратов, оценка дисперсии остатков, построение графика
остатков.
Расчеты представим в таблице 1
Остаточная дисперсия,
показатель адекватности модели, для однофакторного уравнения рассчитывается по
формуле: 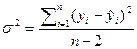 .
.
Используем данные табл. 1 получим: 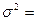 148,22/8=18,53.
148,22/8=18,53.
Чем меньше значение
остаточной дисперсии, тем лучше регрессионное уравнение.
График остатков построим
с помощью инструмента Excel Регрессия.

Рис.1 График остатков
3. Проверка выполнения
предпосылок МНК.
Основными
предположениями классической модели линейной регрессии являются следующие:
1) М(εi)=0,
2)
M(εi2)=δ2 – дисперсия
случайной компоненты – константа,
3)
COV(εi, εj)=0.
Нарушение
тех или иных предпосылок проверяется на
основе выдвижения соответствующих гипотез относительно ε. Оценочными
значениями εi являются
величины yi- i=
i=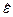 i. Все критерии относительно ε основываются на
этих оценочных значениях.
i. Все критерии относительно ε основываются на
этих оценочных значениях.
Для проверки второго условия
МНК, то есть условия постоянства
дисперсии случайно компоненты ε используем F-статистику, основанную на том, что
величина F
( 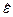 12+
12+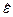 22+ … .+
22+ … .+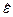 n/22)
n/22)
F=
______________________
( 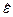 n/2+12+
n/2+12+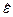 n/2+22+…+
n/2+22+…+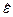 n2)
n2)
подчиняется F-распределению со степенями свободы n/2-1 и n/2-1. Если проверяется гипотеза о
росте дисперсии Fрасч. должно быть меньше Fтабл., если проверяется гипотеза об
уменьшении дисперсии, Fрасч. должно быть больше Fтабл.. Выполнение второго условия называется гомоскедастичностью, а нарушение
его – гетероскедастичностью.
F =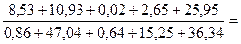
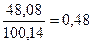 .
.
Табличное значение F- распределения при заданной
вероятности 0,95 и степенях свободы (n/2-1) равно F(0,05; 4;4) =6,39. Fрасч.< Fтабл. Второе условие МНК (гомоскедастичность) с вероятностью 95% нарушено,
принимается гипотеза о росте дисперсии .
Наиболее часто нарушаемым
является третье условие. Показатель ковариации (cov)
устанавливает наличие зависимости между случайными переменными. Поэтому
нарушение третьего условия МНК свидетельствует о зависимости случайных
компонент для наблюдений с различными номерами (i и j). Выполнение этого условия, как
правило, проверяется на основе критерия Дарбина-Уотсона:
D-W= 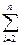 (
(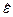 i-
i-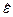 i-1)2
/
i-1)2
/ 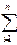
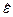 i2 где
i2 где
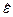 i2
— остатки,
получаемые при оценивании линейной модели наблюдений,
i2
— остатки,
получаемые при оценивании линейной модели наблюдений,
и подчиняется распределению Дарбина-Уотсона,
для которого имеются таблицы квантилей. Сравнивая значения D-Wрасч. и D-Wтабл. можно проверить
гипотезу о нарушении условия 3). Нарушение условия 3) называется
автокорреляцией. При проверке наличия автокорреляции используются табличные
данные. При количестве наблюдений более 10 d1=0,95; d2=1,23.
1)
D-W≤d1 – гипотеза об
отсутствии автокорреляции отвергается;
2)
d2≤ D-W≤4-d2 – гипотеза об отсутствии
автокорреляции принимается;
3)
D-W≥4-d1 –
принимается гипотеза о наличии отрицательной автокорреляции.
Случаи,
когда d1≤D-W≤d2 и 4-d2≤D-W≤4-d1, являются
неопределенными, когда гипотеза не принимается и не отвергается. В этих случаях
обращаются к другим критериям.
Расчет статистики
Дарбина-Уотсона проведем, используя данные
табл.1.2.
D-W = 221,59 / 148,22=0,89.
Критические значения по
таблице распределения статистики Дарбина-Уотсона при n=10 составили d 1 = 0,95 и d2=1,23.
Расчетный
показатель попал в область d1≤D-W≤d2,
гипотеза не принимается и не отвергается.
4. Проверка
значимости параметров уравнения
регрессии с помощью t-критерия Стьюдента (α=0,05).
Проверка
значимости отдельных коэффициентов регрессии связана с определением расчетных значений критерия Стьюдента для
соответствующих коэффициентов регрессии : tрасч = b/ mb и
tрасч = а/ mа.
m b –
стандартная ошибка коэффициента b
ma –
стандартная ошибка коэффициента а
m b = 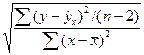 =
= 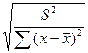 ma=
ma=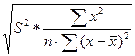
S2 –
остаточная дисперсия на одну степень свободы.
Затем
расчетные значения сравниваются с табличными. Критические значения t-статистики определяется при (n-2) степенях свободы и соответствующем уровне значимости.
Если tрасч
не входит в заданный интервал, то выдвинутая гипотеза о том, что х не
влияет на у, не принимается, т.е. если | tрасч| > t табл коэффициент регрессии считается
значимым.
m b =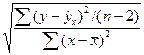 =
=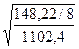 = 0,13
= 0,13
tb = 0,72/0,13=5,57.
Расчетный показатель больше t табл.=2,306 с
заданной вероятностью 95% и не входит в заданный интервал (рис.1.6.).
m
а = 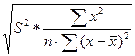 =
=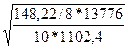 =4,82
=4,82
tа = 12,71/4,82=2,64
. Расчетный показатель больше t
табл. с заданной вероятностью 95% и степенями свободы (n-2) = 2,3.
Гипотеза
о том, что х влияет на у не существенно отклоняется, коэффициенты уравнения
регрессии значимые.
5. Вычисление
коэффициента детерминации, проверка значимости уравнения регрессии с помощью F-критерия Фишера (α=0,05),
относительная ошибка аппроксимации. Вывод о качестве модели.
Величина RXY2 называется коэффициентом детерминации и показывает
долю изменения (вариации) результативного признака под действием факторного
признака. Чем ближе его значение к
единице, тем теснее наблюдения примыкают к линии регрессии, тем лучше регрессия
описывает значимость переменных.
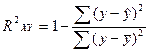 =
=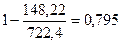
Вариация результата Y (объем выпуска продукции) на 79,5%
объясняется вариацией фактора Х (объем капиталовложений).
F-критерий
Фишера 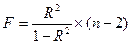 .
.
Если расчетное значение этого критерия со
степенями свободы (m) и (n-m-1), где n- количество наблюдений, m – число включенных в модель факторов, больше табличного
значения критерия Фишера при заданном уровне значимости (достаточно большой
вероятности), то модель признается значимой.
Fрасч
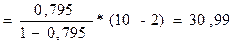
Fрасч больше табличного значения F0,05;1;8 = 5,32, т.е. не входит в правдоподобную область
с плотностью распределения р=0,95 (рис.1.5) – гипотеза о несущественности
уравнения отклоняется. Модель
значима с вероятностью 95%.
6. Прогнозирование среднего значения показателя Y
при уровне значимости α=0,01 при Х=80% от его максимального
значения.
Для прогнозирования
результативного показателя подставим в
уравнение
 =12,71+0,72* x значение факторного
показателя, равного 80% от его максимального значения
=12,71+0,72* x значение факторного
показателя, равного 80% от его максимального значения
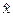 = 0,8*49=39,2.
= 0,8*49=39,2.
Тогда точечный
прогноз составит:  = 12,71+0,72*39,2=41,0.
= 12,71+0,72*39,2=41,0.
7. График фактических и
модельных значений Y, точки прогноза.
График прогноза представим на рисунке 2.
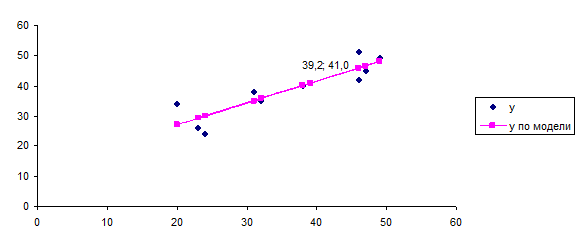
Рис. 2. График по
модели
8. Уравнения нелинейной
регрессии:
8.1 Гиперболическая модель
Уравнение гиперболической
функции:  = a + b/x.
= a + b/x.
Произведем линеаризацию
модели путем замены X = 1/x. В результате получим линейное уравнение  = a + bX.
= a + bX.
Рассчитаем параметры уравнения по данным таблицы 2.
b =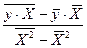 =
=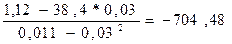
а = 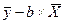 =38,4+704,48*0,03=60,25.
=38,4+704,48*0,03=60,25.
Получим следующее уравнение гиперболической модели:
 = 60,25-704,48/х.
= 60,25-704,48/х.
8.2 Степенная модель
Уравнение степенной
модели имеет вид:  =аxb
=аxb
Для построения этой
модели необходимо произвести линеаризацию переменных. Для этого произведем
логарифмирование обеих частей уравнения : lg  = lg a + b lg x.
= lg a + b lg x.
Обозначим через Y=lg  , X=lg x, A=lg a.
, X=lg x, A=lg a.
Тогда уравнение примет
вид: Y = A + bX – линейное уравнение регрессии. Рассчитаем его параметры, используя
данные таблицы 3.
b = 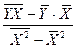 =
=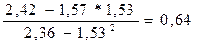
A = 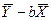 = 1,57-0,64*1,53=0,59
= 1,57-0,64*1,53=0,59
Уравнение регрессии будет
иметь вид: Y = 0,59+0,64* Х.
Перейдем к исходным
переменным x и
y, выполнив потенцирование данного
уравнения.
 = 100,59* х0,64.
= 100,59* х0,64.
Получим уравнение
степенной модели регрессии:
 = 3,87* х0,64.
= 3,87* х0,64.
8.3 Показательная модель
Уравнение показательной
кривой:  =abx.
=abx.
Для построения этой
модели необходимо произвести линеаризацию переменных. Для этого осуществим
логарифмирование обеих частей уравнения:
lg  = lg a + x lg b. Обозначим: Y = lg
= lg a + x lg b. Обозначим: Y = lg  , B = lg b, A = lg a.
, B = lg b, A = lg a.
Получим линейное
уравнение регрессии: Y = A + B x.
Рассчитаем его параметры,
используя данные таблицы 4.
В =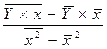 =
=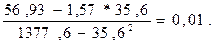
А =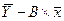 =
1,57-0,01*35,6=1,27
=
1,57-0,01*35,6=1,27
Уравнение будет иметь
вид: Y = 1,27+0,01х.
Перейдем к исходным
переменным x и
y, выполнив потенцирование данного
уравнения:
 =101,27* ( 100,01)х = 18,55*1,02х.
=101,27* ( 100,01)х = 18,55*1,02х.
Графики построенных моделей:
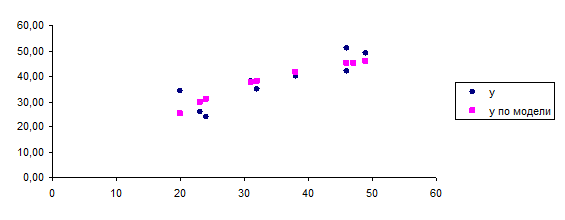
Рис.3. Гиперболическая
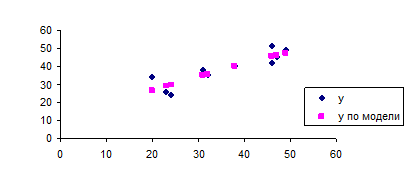
Рис.4. Степенная
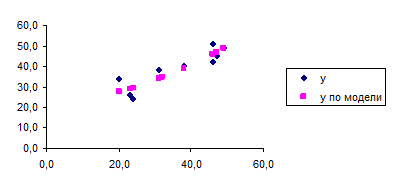
Рис.5. Показательная
9. Сравнение моделей по
характеристикам: коэффициенты детерминации,
коэффициенты эластичности и средние относительные ошибки аппроксимации.
Вывод.
9.1 Гиперболическая модель
Коэффициент детерминации:
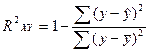 =
=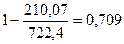
Вариация результата Y на 70,9% объясняется вариацией фактора
Х.
Коэффициент эластичности:
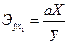 =
=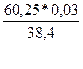 = 0,05.
= 0,05.
Это означает, что при
увеличении фактора Х на 1 % результирующий показатель изменится на 0,05 %.
Бета-коэффициент :
Sx=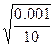 =0,01 Sy=
=0,01 Sy=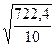 =8,5
=8,5 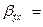 60,25*0,01/8,5=0,07.
60,25*0,01/8,5=0,07.
Т.е. увеличение объема капиталовложений на величину
среднеквадратического отклонения этого показателя приведет к увеличению
среднего значения объема выпуска продукции
на 0,07 среднеквадратического отклонения этого показателя.
Средняя относительная ошибка аппроксимации:
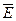 отн = 109,7/ 10= 10,97 %.
отн = 109,7/ 10= 10,97 %.
В среднем расчетные
значения  для гиперболической
модели отличаются от фактических
значений на 10,97%.
для гиперболической
модели отличаются от фактических
значений на 10,97%.
9.2 Степенная модель
Коэффициент детерминации:
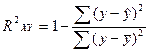 =
=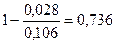
Вариация результата Y на 73,6% объясняется вариацией
фактора Х. Коэффициент эластичности:
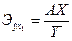 =
=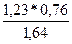 = 0,57.
= 0,57.
Это означает, что при
увеличении факторного признака на 1 % результирующий показатель увеличится на
0,57%.
Бета-коэффициент:
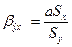 , Sy=
, Sy=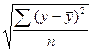 и Sx=
и Sx=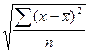 .
.
Sx=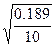 =0,14 Sy=
=0,14 Sy=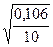 =0,10
=0,10 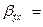 0,59*0,14/0,1=0,78.
0,59*0,14/0,1=0,78.
Т.е. увеличение объема капиталовложений на величину
среднеквадратического отклонения этого показателя приведет к увеличению
среднего значения объема выпуска продукции на 0,78 среднеквадратического
отклонения этого показателя.
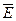 отн=
отн= 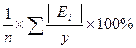 = 93,77/10 = 9,34%.
= 93,77/10 = 9,34%.
В среднем расчетные
значения  для степенной модели
отличаются от фактических значений
на 9,34%.
для степенной модели
отличаются от фактических значений
на 9,34%.
9.3 Показательная модель
Коэффициент детерминации:
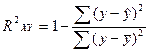 =
=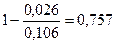
Вариация результата Y на 75,7% объясняется вариацией фактора
Х. Коэффициент эластичности:
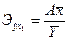
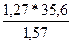 = 28,71.
= 28,71.
Это означает, что при
росте фактора Х на 1 % результирующий показатель Y изменится на 28,71 %.
Бета-коэффициент :
Sx=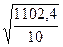 =10,5 Sy=
=10,5 Sy=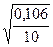 =0,10
=0,10 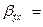 1,27*10,5/0,10=129,10.
1,27*10,5/0,10=129,10.
Т.е. увеличение объема капиталовложений на величину
среднеквадратического отклонения этого показателя приведет к увеличению
среднего значения объема выпуска продукции
на 129,1 среднеквадратического отклонения этого показателя.
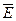 отн= 91,9/ 10 = 9,19%.
отн= 91,9/ 10 = 9,19%.
В среднем расчетные
значения  для показательной
модели отличаются от фактических
значений на 9,19%.
для показательной
модели отличаются от фактических
значений на 9,19%.
Вывод.
Лучшей из уравнений нелинейной
регрессии является показательная:
выше коэффициент детерминации, наименьшая
относительная ошибка. Модель можно использовать для прогнозирования.
Таблица
1
|
n
|
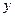
|
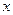
|
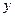 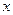
|
|
(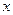 - -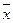 )2 )2
|
(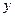 - -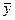 )2 )2
|
(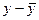 )* )*
*(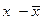 ) )
|

|
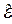 = =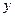 - -
|
(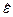 i- i-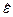 i-1)2 i-1)2
|
ЕОТН
|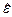 / /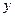 |* |*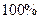
|
(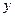 - - )2 )2
|
|
1
|
38,0
|
31
|
1178,00
|
961,00
|
21,16
|
0,16
|
1,84
|
35,08
|
2,92
|
|
7,68
|
8,53
|
|
2
|
26,0
|
23
|
598,00
|
529,00
|
158,76
|
153,76
|
156,24
|
29,31
|
-3,31
|
38,77
|
12,72
|
10,93
|
|
3
|
40,0
|
38
|
1520,00
|
1444,00
|
5,76
|
2,56
|
3,84
|
40,13
|
-0,13
|
10,08
|
0,33
|
0,02
|
|
4
|
45,0
|
47
|
2115,00
|
2209,00
|
129,96
|
43,56
|
75,24
|
46,63
|
-1,63
|
2,24
|
3,62
|
2,65
|
|
5
|
51,0
|
46
|
2346,00
|
2116,00
|
108,16
|
158,76
|
131,04
|
45,91
|
5,09
|
45,18
|
9,99
|
25,95
|
|
6
|
49,0
|
49
|
2401,00
|
2401,00
|
179,56
|
112,36
|
142,04
|
48,07
|
0,93
|
17,35
|
1,90
|
0,86
|
|
7
|
34,0
|
20
|
680,00
|
400,00
|
243,36
|
19,36
|
68,64
|
27,14
|
6,86
|
35,16
|
20,17
|
47,04
|
|
8
|
35,0
|
32
|
1120,00
|
1024,00
|
12,96
|
11,56
|
12,24
|
35,80
|
-0,80
|
58,68
|
2,29
|
0,64
|
|
9
|
42,0
|
46
|
1932,00
|
2116,00
|
108,16
|
12,96
|
37,44
|
45,91
|
-3,91
|
9,63
|
9,30
|
15,25
|
|
10
|
24,0
|
24
|
576,00
|
576,00
|
134,56
|
207,36
|
167,04
|
30,03
|
-6,03
|
4,51
|
25,12
|
36,34
|
|
Итого
|
384,0
|
356
|
14466,00
|
13776,00
|
1102,40
|
722,40
|
795,60
|
|
|
221,59
|
93,11
|
148,22
|
|
средн.
|
38,4
|
35,60
|
1446,60
|
1377,60
|
|
|
|
|
|
|
9,31
|
|
Таблица 2
|
t
|
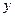
|
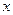
|
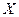
|
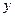 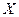
|
 2 2
|
(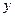 - -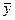 ) )
|
(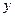 - -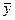 )2 )2
|
(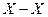 ) )
|
(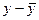 ) )
*(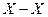 ) )
|
(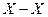 )2 )2
|

|
(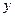 - - )2 )2
|
ЕОТН
|
(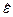 i- i-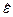 i-1)2 i-1)2
|
|
1
|
38,0
|
31
|
0,03
|
1,23
|
0,0010
|
-0,40
|
0,16
|
0,001
|
0,00
|
0,0000015
|
37,52
|
0,23
|
1,26
|
|
|
2
|
26,0
|
23
|
0,04
|
1,13
|
0,0019
|
-12,40
|
153,76
|
0,012
|
-0,15
|
0,0001554
|
29,62
|
13,09
|
13,92
|
16,8
|
|
3
|
40,0
|
38
|
0,03
|
1,05
|
0,0007
|
1,60
|
2,56
|
-0,005
|
-0,01
|
0,0000221
|
41,71
|
2,92
|
4,27
|
3,65
|
|
4
|
45,0
|
47
|
0,02
|
0,96
|
0,0005
|
6,60
|
43,56
|
-0,010
|
-0,06
|
0,0000948
|
45,26
|
0,07
|
0,58
|
2,1
|
|
5
|
51,0
|
46
|
0,02
|
1,11
|
0,0005
|
12,60
|
158,76
|
-0,009
|
-0,12
|
0,0000860
|
44,93
|
36,80
|
11,90
|
40,02
|
|
6
|
49,0
|
49
|
0,02
|
1,00
|
0,0004
|
10,60
|
112,36
|
-0,011
|
-0,11
|
0,0001125
|
45,87
|
9,79
|
6,39
|
8,63
|
|
7
|
34,0
|
20
|
0,05
|
1,70
|
0,0025
|
-4,40
|
19,36
|
0,019
|
-0,08
|
0,0003605
|
25,02
|
80,56
|
26,40
|
34,18
|
|
8
|
35,0
|
32
|
0,03
|
1,09
|
0,0010
|
-3,40
|
11,56
|
0,000
|
0,00
|
0,0000001
|
38,23
|
10,45
|
9,24
|
149,06
|
|
9
|
42,0
|
46
|
0,02
|
0,91
|
0,0005
|
3,60
|
12,96
|
-0,009
|
-0,03
|
0,0000860
|
44,93
|
8,60
|
6,98
|
0,09
|
|
10
|
24,0
|
24,0
|
0,04
|
1,00
|
0,0017
|
-14,40
|
207,36
|
0,011
|
-0,15
|
0,0001135
|
30,89
|
47,54
|
28,73
|
15,69
|
|
Итого
|
384,0
|
356
|
0,31
|
11,18
|
0,0107
|
|
722,40
|
|
-0,73
|
0,0010323
|
384,00
|
210,07
|
109,7
|
270,20
|
|
Средн
|
38,40
|
35,60
|
0,03
|
1,12
|
0,0011
|
|
|
|
|
|
|
|
10,97
|
|
Таблица 3.
|
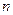
|
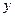
|
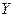
|
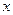
|
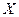
|
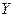 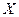
|
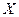 2 2
|
(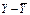 )2 )2
|
(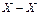 )2 )2
|
(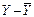 )* )*
(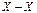 ) )
|
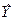
|
(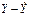 )2 )2
|

|
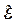
|
(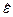 i- i-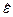 i-1)2 i-1)2
|
ЕОТН
|
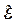 2 2
|
|
1
|
38
|
1,58
|
31
|
1,49
|
2,36
|
2,22
|
0,0001
|
0,00155
|
0,000
|
1,55
|
0,00105
|
2,73
|
|
7,20
|
7,5
|
38
|
|
2
|
26
|
1,41
|
23
|
1,36
|
1,93
|
1,85
|
0,0249
|
0,02855
|
0,0266
|
1,46
|
0,0024
|
-3,10
|
34,04
|
11,92
|
9,61
|
26
|
|
3
|
40
|
1,60
|
38
|
1,58
|
2,53
|
2,50
|
0,0009
|
0,00241
|
0,0014
|
1,60
|
0,00000
|
-0,20
|
8,38
|
0,51
|
0,04
|
40
|
|
4
|
45
|
1,65
|
47
|
1,67
|
2,76
|
2,80
|
0,0065
|
0,01999
|
0,0114
|
1,66
|
0,0001
|
-1,10
|
0,80
|
2,45
|
1,2
|
45
|
|
5
|
51,0
|
1,71
|
46
|
1,66
|
2,84
|
2,76
|
0,0182
|
0,01744
|
0,018
|
1,66
|
0,00249
|
5,53
|
44,01
|
10,85
|
30,62
|
51,0
|
|
6
|
49,0
|
1,69
|
49
|
1,69
|
2,86
|
2,86
|
0,0138
|
0,02544
|
0,0187
|
1,68
|
0,0002
|
1,65
|
15,11
|
3,36
|
2,71
|
49,0
|
|
7
|
34,0
|
1,53
|
20
|
1,30
|
1,99
|
1,69
|
0,0017
|
0,05275
|
0,009
|
1,42
|
0,0114
|
7,40
|
33,16
|
21,78
|
54,8
|
34,0
|
|
8
|
35
|
1,54
|
32
|
1,51
|
2,32
|
2,27
|
0,0008
|
0,00065
|
0,001
|
1,56
|
0,0001
|
-0,99
|
70,52
|
2,84
|
0,99
|
35
|
|
9
|
42
|
1,62
|
46
|
1,66
|
2,70
|
2,76
|
0,0026
|
0,01744
|
0,007
|
1,66
|
0,001186
|
-3,47
|
6,12
|
8,25
|
12,02
|
42
|
|
10
|
24
|
1,38
|
24,0
|
1,38
|
1,90
|
1,90
|
0,0370
|
0,02265
|
0,029
|
1,48
|
0,00914
|
-5,91
|
6,0
|
24,62
|
35
|
24
|
|
∑
|
384
|
15,73
|
356
|
15,31
|
24,2
|
23,6
|
0,106
|
0,189
|
0,122
|
0,00
|
0,0281
|
|
218,1
|
93,77
|
154,4
|
384
|
|
Ср
|
38,4
|
1,57
|
35,6
|
1,53
|
2,42
|
2,36
|
|
|
|
|
|
|
|
9,38
|
|
38,4
|
Таблица
4.
|
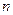
|
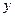
|
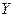
|
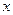
|
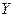 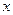
|
 2 2
|
(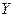 - -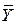 ) )
|
(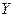 - -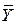 )2 )2
|
(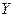 - -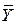 ) )
*(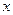 - -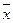 ) )
|
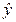
|
(y- )2 )2
|
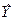
|
(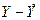 )2 )2
|
ЕОТН
|
(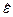 i- i-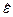 i-1)2 i-1)2
|
|
1
|
38,0
|
1,58
|
31,0
|
48,97
|
961,00
|
0,007
|
0,0001
|
-0,03
|
34,15
|
14,85
|
1,533
|
0,0022
|
10,14
|
|
|
2
|
26,0
|
1,41
|
23,0
|
32,54
|
529,00
|
-0,158
|
0,0249
|
1,99
|
29,17
|
10,06
|
1,465
|
0,0025
|
-12,20
|
49,3420
|
|
3
|
40,0
|
1,60
|
38,0
|
60,88
|
1444,00
|
0,029
|
0,0009
|
0,07
|
39,19
|
0,65
|
1,593
|
0,0001
|
2,02
|
15,83
|
|
4
|
45,0
|
1,65
|
47,0
|
77,70
|
2209,00
|
0,081
|
0,0065
|
0,92
|
46,79
|
3,20
|
1,670
|
0,0003
|
-3,98
|
6,74
|
|
5
|
51,0
|
1,71
|
46,0
|
78,55
|
2116,00
|
0,135
|
0,0182
|
1,40
|
45,88
|
26,25
|
1,662
|
0,0021
|
10,05
|
47,78
|
|
6
|
49,0
|
1,69
|
49,0
|
82,82
|
2401,00
|
0,118
|
0,01381
|
1,57
|
48,67
|
0,11
|
1,687
|
0,0000
|
0,68
|
22,95
|
|
7
|
34,0
|
1,53
|
20,0
|
30,63
|
400,00
|
-0,041
|
0,0017
|
0,64
|
27,5
|
42,27
|
1,439
|
0,0085
|
19,12
|
38,06
|
|
8
|
35,0
|
1,54
|
32,0
|
49,4
|
1024,00
|
-0,029
|
0,0008
|
0,10
|
34,8
|
0,03
|
1,542
|
0,0000
|
0,50
|
40,04
|
|
9
|
42,0
|
1,62
|
46,0
|
74,67
|
2116,00
|
0,051
|
0,0026
|
0,53
|
45,88
|
15,03
|
1,662
|
0,0015
|
-9,23
|
16,41
|
|
10
|
24,0
|
1,38
|
24,0
|
33,13
|
576,00
|
-0,192
|
0,0370
|
2,23
|
29,75
|
33,08
|
1,474
|
0,0087
|
-23,96
|
3,51
|
|
Итого
|
384,0
|
15,73
|
356,0
|
569,3
|
13776,00
|
|
0,1064
|
9,42
|
|
145,52
|
|
0,0258
|
91,87
|
240,67
|
|
Средн
|
38,4
|
1,57
|
35,60
|
56,93
|
1377,60
|
|
|
0,94
|
|
|
|
|
|
|
Задание 2
1. Рассчитать параметры линейного
уравнения множественной регрессии с полным перечнем факторов.
2. Оценить статистическую значимость
параметров регрессионной модели с помощью t-критерия, проверить нулевую гипотезу
о значимости уравнения регрессии с помощью F-критерия (α=0,05), оценить
качество уравнения регрессии с помощью коэффициента детерминации.
3. Используя пошаговую множественную
регрессию (метод исключения или метод включения), построить модель формирования
прибыли от реализации за счет значимых факторов.
4. Дать оценку влияния значимых факторов
с помощью коэффициентов эластичности, бета- и дельта- коэффициентов.
5. Рассчитать прогнозные значения
результатов, если прогнозные значения факторов составляют 80% от их максимального
значений.