СОДЕРЖАНИЕ
Задача 2. 3
Задача 3. 8
Задача 4. 14
Задача 5. 16
Задача 6. 18
Задача 7. 22
СПИСОК ЛИТЕРАТУРЫ.. 25
Задача 2
Для изучения
дифференциации процентных ставок по вкладам населения в отделении банка
проведена 5-процентная механическая выборка. В результате получено следующее
распределение вкладов по срокам хранения:
|
Группа вкладов по сроку хранения, дней
|
Число вкладов
|
|
До 30
|
98
|
|
30 – 60
|
140
|
|
60 – 90
|
175
|
|
90 – 180
|
105
|
|
180 – 360
|
56
|
|
360 и более
|
26
|
|
Итого:
|
600
|
Определите:
1) средний срок хранения
вкладов по вкладам, включенным в выборку;
2) долю вкладов со сроком
хранения более 180 дней, по вкладам,
включенным в выборку;
3) с вероятностью 0,954
пределы, в которых можно ожидать среднюю продолжительность хранения вклада и
доли вкладов со сроком более 180 дней в целом по отделению банка;
4) необходимую
численность выборки при определении доли вкладов со сроком хранения более 180
дней, чтобы с вероятностью 0,683 предельная ошибка выборки не превысила 7%.
Решение
1) Средний срок хранения
вкладов определяют по формуле средней арифметической взвешенной:
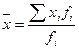 ,
(1)
,
(1)
где 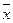 – среднее значение признака;
– среднее значение признака;
х – индивидуальное значение признака;
f – частота повторения xi значения признака.
Для расчета среднего
срока хранения вкладов необходимо варианты признака выразить одним числом
(дискретным). За такое дискретное число принимается средняя арифметическая
простая из верхнего и нижнего значения интервала.
Например, для второй
группы: (30,0+60,0)/2 = 45 дней
Так как первый и
последний интервал является открытыми, то величина интервала первой группы
принимается равной величине интервала последующей (30,0), а величина интервала
последней группы – величине интервала предыдущей группы (180,0). Таким образом,
условно принимаем:
1 группа: 0 – 30,0
5 группа: 360,0 – 540,0
Определим средние
величины интервалов:
1 группа: 15 дней
2 группа: 45 дней
3 группа: 75 дней
4 группа: 135 дней
5 группа: 270 дней
6 группа: 450 дней
Тогда средний срок
хранения вкладов составит:
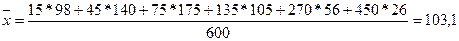 дней
дней
2) Доля определяется по
формуле:
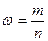 , (2)
, (2)
где m – число единиц в выборочной
совокупности, обладающих данным признаком;
n – численность выборочной
совокупности.
Вкладов со сроком
хранения более 180 дней в исследуемой совокупности имеется 56+26 = 82, всего
600 вкладов, тогда доля составит вкладов со сроком хранения более 180 дней
составит:
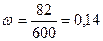
14% в совокупности
составляют вклады со сроком хранения более 180 дней.
3) Границы средней в
генеральной совокупности определяются:
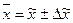 (3)
(3)
или
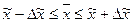 ,
(4)
,
(4)
где 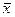 – средняя в генеральной совокупности,
– средняя в генеральной совокупности,
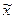 – средняя в выборочной совокупности,
– средняя в выборочной совокупности,
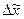 – предельная ошибка выборочной средней.
– предельная ошибка выборочной средней.
Предельная ошибка
выборочной средней определяется по формуле:
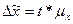 ,
(5)
,
(5)
где t – коэффициент доверия, при уровне
вероятности 0,954 t = 2,0;
μх – средняя ошибка
выборочной средней.
Для механической выборки
средняя ошибка выборочной средней определяется по формуле:
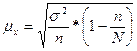 ,
(6)
,
(6)
где s2 – показатель вариации признака
(дисперсия);
n – численность выборочной
совокупности;
N – численность генеральной
совокупности;
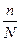 – доля отбора.
– доля отбора.
Границы
генеральной доли определяются:
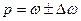 (7)
(7)
или
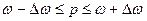 ,
(8)
,
(8)
где р – генеральная доля (удельный
вес единиц генеральной совокупности, обладающих данным признаком), выражается в
коэффициентах или в процентах;
m – число единиц в выборочной
совокупности, обладающих данным признаком;
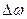 – предельная ошибка
доли.
– предельная ошибка
доли.
Предельная ошибка доли
рассчитывается по формуле:
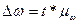 ,
(9)
,
(9)
где 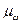 – средняя ошибка доли.
– средняя ошибка доли.
Для механической выборки средняя
ошибка доли определяется по формуле:
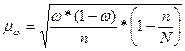 (10)
(10)
Определим дисперсию по
следующей формуле:
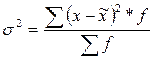 (11)
(11)
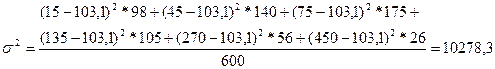
N = 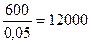
Определим среднюю ошибку
выборочной средней:
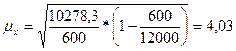
Определим предельную
ошибку выборочной средней:
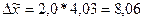
Определим границы средней
в генеральной совокупности:
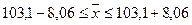
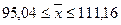
С вероятностью 0,954
пределы, в которых можно ожидать среднюю продолжительность хранения вклада составляют
от 95,04 дней до 111,16 дней.
Определим среднюю ошибку
доли:
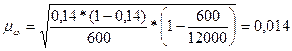
Определим предельную
ошибку доли:
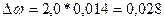
Определим
границы генеральной доли:
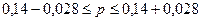
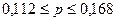
С вероятностью 0,954 доля
вкладов со сроком хранения более 180 дней находится в пределах от 11,2% до 16,8%.
Задача 3
По одному из предприятий
имеются следующие данные об объеме производства мясных консервов:
|
Год
|
Объем производства мясных консервов, тыс. усл. банок
|
|
1987
|
70
|
|
1988
|
80
|
|
1989
|
90
|
|
1990
|
110
|
|
1991
|
120
|
|
1992
|
130
|
|
1993
|
140
|
|
1994
|
150
|
|
1995
|
170
|
|
1996
|
180
|
|
1997
|
190
|
Для анализа динамики
производства мясных консервов исчислите: среднегодовое их производство,
базисные, цепные и среднегодовые показатели абсолютного прироста, темпов роста
и прироста.
Используя уравнение
прямой, проверьте анализируемый ряд динамики производства мясных консервов на
наличие тренда.
Изобразите динамику
производства мясных консервов на графике. Сделайте выводы.
Решение
Средний уровень ряда
динамики определяется по формуле средней арифметической простой:
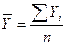 (12)
(12)
Среднегодовое
производство мясных консервов составит:
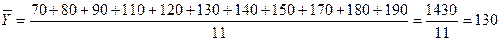 тыс. усл. банок
тыс. усл. банок
Абсолютный прирост
(∆i) определяется как разность между двумя уровнями
динамического ряда. При сравнении с постоянной базой он равен:
∆i б =Yi – Y0,
(13)
где ∆i б − абсолютный прирост базисный;
Yi − уровень сравниваемого
периода;
Y0 − уровень базисного периода.
При сравнении с
переменной базой абсолютный прирост равен:
∆i ц =Yi – Yi-1, (14)
где ∆i ц − абсолютный прирост цепной;
Yi-1− уровень непосредственно
предшествующего периода.
Темп роста (Тр)
определяется как отношение двух
сравниваемых уровней.
При сравнении с
постоянной базой:
Трб =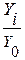 *100
%
(15)
*100
%
(15)
При сравнении с переменной базой:
Трц
=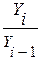 *100
%
(16)
*100
%
(16)
Темп прироста определяет
разность между темпом роста (в %) и 100%:
Тпр = Тр – 100% (17)
Определим цепные и
базисные показатели динамики производства мясных консервов в 1988 и 1989 гг.
Абсолютные приросты
составят:
– цепные:
∆1988 ц
= 80 – 70 = 10 тыс. усл. банок
∆1989 ц
= 90 – 80 = 10 тыс. усл. банок
– базисные:
∆1988 б
= 80 – 70 = 10 тыс. усл. банок
∆1989 б
= 90 – 70 = 20 тыс. усл. банок
Темпы роста составят:
– цепные:
Тр1988 ц =
80 / 70 *100 = 114,3%
Тр1989 ц =
90 / 80 *100 = 112,5%
– базисные:
Тр1988 б =
80 / 70 *100 = 114,3%
Тр1989 б =
90 / 70 *100 = 128,6%
Темпы прироста составят:
– цепные:
Тпр1988 ц
= 114,3 – 100 = 14,3%
Тпр1989 ц
= 112,5 – 100 = 12,5%
– базисные:
Тпр1988 б
= 114,3 – 100 = 14,3%
Тпр1989 б
= 128,6 – 100 = 28,6%
Расчет остальных показателей ведется
аналогичным образом, результаты расчетов представим в таблице 1.
Средний абсолютный
прирост определяется по формуле:
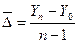 (18)
(18)
Определим средний
абсолютный прирост:
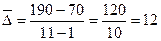 тыс. усл. банок
тыс. усл. банок
Средний темп роста
определяется по формуле:
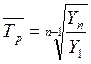 (19)
(19)
Средний темп роста
составит:
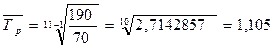 , или 110,5%
, или 110,5%
Средний темп прироста
определяется по формуле:
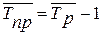 (20)
(20)
Средний темп прироста составит:
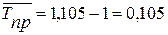 , или 10,5%
, или 10,5%
Таблица 1
Показатели динамики производства
мясных консервов с 1987 г.
по 1997 г.
|
Годы
|
Объем производства
мясных консервов, тыс. усл. банок
|
Абсолют-ный прирост
цепной, тыс. усл. б.
|
Абсолют-ный прирост
базисный, тыс. усл. б.
|
Темп роста цеп-ной,
%
|
Темп роста
базис-ный,
%
|
Темп прироста
цепной,
%
|
Темп прироста
базис-ный,
%
|
|
1987
|
70
|
–
|
–
|
–
|
–
|
–
|
–
|
|
1988
|
80
|
10
|
10
|
114,3
|
114,3
|
14,3
|
14,3
|
|
1989
|
90
|
10
|
20
|
112,5
|
128,6
|
12,5
|
28,6
|
|
1990
|
110
|
20
|
40
|
122,2
|
157,1
|
22,2
|
57,1
|
|
1991
|
120
|
10
|
50
|
109,1
|
171,4
|
9,1
|
71,4
|
|
1992
|
130
|
10
|
60
|
108,3
|
185,7
|
8,3
|
85,7
|
|
1993
|
140
|
10
|
70
|
107,7
|
200,0
|
7,7
|
100,0
|
|
1994
|
150
|
10
|
80
|
107,1
|
214,3
|
7,1
|
114,3
|
|
1995
|
170
|
20
|
100
|
113,3
|
242,9
|
13,3
|
142,9
|
|
1996
|
180
|
10
|
110
|
105,9
|
257,1
|
5,9
|
157,1
|
|
1997
|
190
|
10
|
120
|
105,6
|
271,4
|
5,6
|
171,4
|
|
В среднем
|
130
|
12
|
─
|
110,5
|
─
|
10,5
|
─
|
Проверим анализируемый
ряд динамики производства мясных консервов на наличие тренда, используя
уравнение прямой.
Уравнение прямой имеет
вид:
у = а+bt, (21)
Расчет
коэффициентов а и b
ведется на основе метода наименьших квадратов. Для нахождения этих
коэффициентов решим систему уравнений:
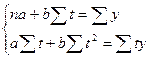
 (22)
(22)
Составим расчетную таблицу 2.
Так как ∑t = 0, то имеем:
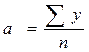 и
и 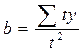
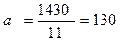
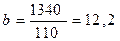
Следовательно, уравнение прямой примет вид:
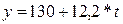
Таблица 2
|
Годы
|
Объем производства мясных консервов, тыс. усл. банок
(У)
|
Условное время (t)
|
t2
|
tу
|
Теоретические уровни
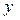 = 130+12,2*t = 130+12,2*t
|
|
1987
|
70
|
-5
|
25
|
-350
|
69,0
|
|
1988
|
80
|
-4
|
16
|
-320
|
81,2
|
|
1989
|
90
|
-3
|
9
|
-270
|
93,4
|
|
1990
|
110
|
-2
|
4
|
-220
|
105,6
|
|
1991
|
120
|
-1
|
1
|
-120
|
117,8
|
|
1992
|
130
|
0
|
0
|
0
|
130,0
|
|
1993
|
140
|
1
|
1
|
140
|
142,2
|
|
1994
|
150
|
2
|
4
|
300
|
154,4
|
|
1995
|
170
|
3
|
9
|
510
|
166,6
|
|
1996
|
180
|
4
|
16
|
720
|
178,8
|
|
1997
|
190
|
5
|
25
|
950
|
191,0
|
|
Итого
|
1 430
|
0
|
110
|
1 340
|
1 430
|
Определим теоретические
уровни, подставив в уравнение прямой параметры t,
результаты расчетов представим в таблице 2.
Изобразим динамику
производства мясных консервов на графике (Рис.1).
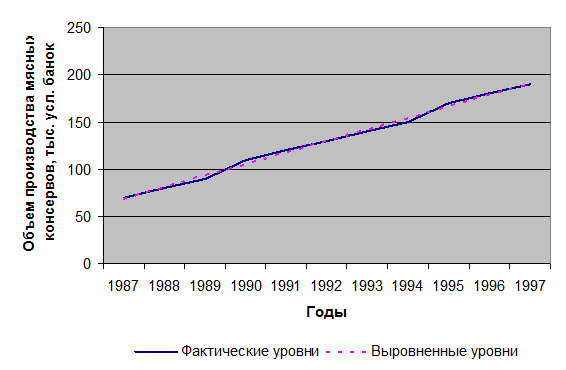
Рис. 1 Динамика производства мясных консервов
с 1987 г.
по 1997 г.
Можно сделать следующие
выводы: в период с 1987 г.
по 1997 г.
производство мясных консервов с каждым годом увеличивалось. Среднегодовое
производство мясных консервов составило 130 тыс. усл. банок. В среднем в год
производство мясных консервов увеличивалось на 12 тыс. усл. банок, или на
10,5%.
Проверка динамики
производства мясных консервов на наличие тренда показала, что на исследуемом
предприятии имеется устойчивая тенденция увеличения производства мясных
консервов.
Задача 4
Себестоимость выпускаемого
печенья на фабрике по сравнению с прошлым годом осталась неизменной.
Себестоимость конфет в среднем возросла на 5%. Общие затраты на выпуск печенья
по фабрике в отчетном году составили 500 тыс. руб., на выпуск конфет – 1300
тыс. руб.
Определите:
1) как изменилась
себестоимость выпускаемой продукции в среднем по кондитерской фабрике;
2) общую сумму затрат
вследствие изменения себестоимости.
Сделайте выводы.
Решение
Общий индекс
себестоимости определяется по формуле:
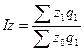 ,
(23)
,
(23)
где 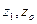 – себестоимость
соответственно в отчетном и базисном периоде;
– себестоимость
соответственно в отчетном и базисном периоде;
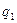 – физический объем производства
в отчетном периоде.
– физический объем производства
в отчетном периоде.
Так как по условию задачи
известно изменение себестоимости печенья и конфет (индивидуальные индексы
себестоимости), то преобразуем агрегатную форму индекса себестоимости в средний
гармонический индекс себестоимости:
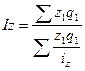 ,
(24)
,
(24)
где iz – индивидуальный индекс
себестоимости;
∑z1q1 – общие затраты на выпуск продукции
в отчетном периоде.
Так как себестоимость выпускаемого
печенья на фабрике по сравнению с прошлым годом осталась неизменной, то индивидуальный
индекс себестоимости печенья равен 1,00. Так как себестоимость конфет в среднем
возросла на 5%, то индивидуальный индекс себестоимости конфет равен 1,05.
Определим общий индекс себестоимости
выпускаемой продукции в среднем по кондитерской фабрике:
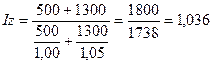 , или 103,6%
, или 103,6%
Роль отдельных факторов может быть
определена как разность числителя и знаменателя соответствующего индекса.
Роль себестоимости в изменении общей
суммы затрат на производство определяется как разность числителя и знаменателя
индекса себестоимости:
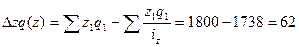 тыс. руб.
тыс. руб.
По результатам расчетов можно сделать
следующий вывод:
В отчетном периоде по сравнению с
базисным периодом себестоимость выпускаемой продукции в среднем по кондитерской
фабрике увеличилась на 3,6%, вследствие этого общая сумма затрат на выпуск
продукции выросли на 62 тыс. рублей.
Задача 5
По материалам
обследования домашних хозяйств получены следующие данные:
|
Показатель
|
В составе совокупных доходов семьи
|
Всего
|
|
Есть доход от предпринимательской деятельности
|
Нет дохода от предпринимательской деятельности
|
|
Доход выше прожиточного
минимума
Доход ниже прожиточного
минимума
|
140
70
|
100
340
|
240
410
|
|
Итого
|
210
|
440
|
650
|
Для оценки тесноты связи
между источниками доходов (наличием дохода от предпринимательской деятельности)
и размером дохода найдите коэффициент ассоциации.
Решение
Коэффициент ассоциации
определяется по формуле:
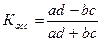 (25)
(25)
Связь считается
подтвержденной, если Касс > 0,5.
Составим расчетную
таблицу 3.
Таблица 3
|
Показатель
|
В составе
совокупных доходов семьи
|
Всего
|
|
Есть доход
от предпринимательской деятельности
|
Нет дохода
от предпринимательской деятельности
|
|
Доход выше прожиточного минимума
Доход ниже прожиточного минимума
|
140 (а)
70 (с)
|
100 (b)
340 (d)
|
240
410
|
|
Итого
|
210
|
440
|
650
|
Тогда коэффициент ассоциации составит:
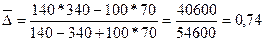
Можно сделать вывод, что связь между источниками доходов
(наличием дохода от предпринимательской деятельности) и размером дохода
существенная.
Задача 6
На начало года
численность наличного населения одного из районов области составляла 31180
человек, временно проживающих было 420 человек, а из числа постоянно
проживающего населения временно отсутствовало 680 человек. Из общего числа
постоянно проживающего населения лиц моложе трудоспособного возраста было 7940
человек, а старше трудоспособного возраста 7400 человек.
В течение года родилось
340 человек, умерло 432 человека, выехало в другие районы на постоянное
жительство 937 человек и переехало на постоянное жительство в район из других местностей
919 человек.
Определить:
1) численность
постоянного населения района на начало и конец года;
2) среднегодовую
численность постоянного населения района;
3) показатели
естественного движения: коэффициенты рождаемости, смертности, естественного прироста,
жизненности, оборота населения, экономичности производства;
4) показатели миграции:
коэффициенты прибытия, убытия, миграции;
5) показатели возрастной
структуры населения.
Проанализируйте
полученные показатели. Сделайте выводы о динамике и источниках роста (снижения)
численности постоянного населения района. Назовите виды рассчитанных относительных
и средних величин.
Решение
Численность постоянного
населения района на начало года (Sн.г.) определим следующим образом:
Sн.г. = НН + ВО – ВП , (26)
где НН – наличное население;
ВО – временно отсутствующие;
ВП – временно проживающие.
Численность постоянного населения
района на начало года составит:
Sн.г. = 31180+680–420 = 31440 человек
Численность постоянного населения
района на конец года рассчитаем по формуле:
Sк.г. = Sн.г.+ N – M +П – В, (27)
где N – число родившихся;
М – число умерших;
П – число прибывших в данную местность;
В – число выбывших в другие районы.
Численность постоянного населения
района на конец года составит:
Sк.г. = 31440+340–432+919–937 = 31330
человек
Среднегодовую численность определим
по формуле средней арифметической простой:
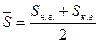 (28)
(28)
Среднегодовая численность постоянного
населения района составит:
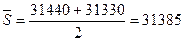 человек
человек
Коэффициент рождаемости
определяется по формуле:
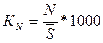 (29)
(29)
Коэффициент рождаемости составит:
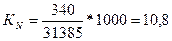 ‰
‰
Коэффициент смертности определяется
по формуле:
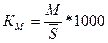 (30)
(30)
Коэффициент смертности
составит:
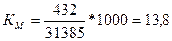 ‰
‰
Коэффициент естественного прироста определяется как разница
между коэффициентом рождаемости и коэффициентом смертности:
KN-M = KN – KM (31)
Коэффициент естественного прироста составит:
KN-M = 10,8 – 13,8 = -3 ‰
Коэффициент жизненности определяется по формуле:
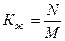 (32)
(32)
Коэффициент жизненности составит:
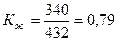
Коэффициент оборота населения рассчитывается по формуле:
KN+M = KN + KM
(33)
Коэффициент оборота населения составит:
KN+M = 10,8+13,8 = 24,6 ‰
Коэффициент
экономичности
производства определяется по формуле:
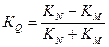 (34)
(34)
Коэффициент
экономичности
производства составит:
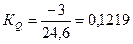
Коэффициент
прибытия определяется по
формуле:
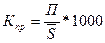 (35)
(35)
Коэффициент
прибытия составит:
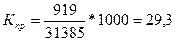 ‰
‰
Коэффициент
убытия определяется по
формуле:
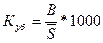 (36)
(36)
Коэффициент
убытия составит:
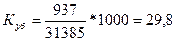 ‰
‰
Коэффициент
миграции определяется по
формуле:
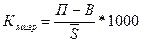 (37)
(37)
Коэффициент
миграции составит:
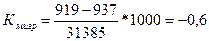 ‰
‰
По
условию задачи из общего
числа постоянно проживающего населения лиц моложе трудоспособного возраста было
7940 человек, а старше трудоспособного возраста 7400 человек. Тогда число лиц
трудоспособного возраста составит: Sтруд. = 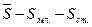 = 31385 – 7940 – 7400 = 16045 человек
= 31385 – 7940 – 7400 = 16045 человек
Определим доли возрастных групп в общей численности
населения:
Доля трудоспособных в общей численности населения составит:
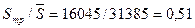 , или 51%
, или 51%
Доля лиц, старше трудоспособных в общей численности населения составит:
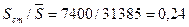 , или 24%
, или 24%
Доля лиц, младше трудоспособных в общей численности населения составит:
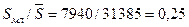 , или 25%
, или 25%
Численность
постоянного населения района снизилась на 110 человек.
Так как коэффициент естественного прироста отрицателен, то за
счет естественного прироста численность постоянного населения района уменьшилась.
Число умерших превысило число родившихся.
Численность постоянного населения района снизилась за счет
миграции населения – числа выбывших в другие районы на постоянное жительство. Число выбывших
превысило число прибывших на постоянное жительство в район из других
местностей.
При расчете среднегодовой
численности населения была использована средняя арифметическая простая. При
расчете показателей возрастной структуры населения (долей) были использованы
относительные величины структуры.
Задача 7
Имеются следующие данные
о кредитных вложениях в экономику (на начало мес., млрд. руб.):
|
|
Январь
|
Апрель
|
Июль
|
|
Кредитные вложения, всего
В том числе:
краткосрочные
долгосрочные
|
83,6
79,3
4,3
|
106,0
91,7
14,3
|
112,9
98,7
14,2
|
Определите:
1) структуру кредитных
вложений в экономику по периодам;
2) как изменился объем
кредитных вложений всего и в том числе краткосрочных и долгосрочных;
3) оцените изменение
структуры кредитных вложений, исчислив линейный (квадратический) коэффициент
структурных сдвигов, оцените глубину структурных изменений кредитных вложений.
Сделайте выводы.
Решение
Определим структуру
кредитных вложений в экономику по периодам. Результаты представим в таблице 4.
Таблица 4
Структура кредитных вложений в
экономику по периодам
|
Показатель
|
Январь
|
Апрель
|
Июль
|
|
млрд. руб.
|
удельный вес, %
|
млрд. руб.
|
удельный вес, %
|
млрд. руб.
|
удельный вес, %
|
|
Кредитные вложения, всего
В том числе
|
83,6
|
100,0
|
106,0
|
100,0
|
112,9
|
100,0
|
|
краткосрочные
|
79,3
|
95,0
|
91,7
|
86,0
|
98,7
|
87,0
|
|
долгосрочные
|
4,3
|
5,0
|
14,3
|
14,0
|
14,2
|
13,0
|
Рассмотрим, как изменился
объем кредитных вложений всего и в том числе краткосрочных и долгосрочных с
помощью темпов роста и прироста:
1) всего кредитных
вложений:
– в апреле по сравнению с
январем:
Тр = 106,0/83,6*100 =
126,8%
Тпр = 126,8 – 100 = 26,8%
– в июле по сравнению с
апрелем:
Тр = 112,9/106,0*100 =
106,5%
Тпр = 106,5 – 100 = 6,5%
2) краткосрочных
кредитных вложений:
– в апреле по сравнению с
январем:
Тр = 91,7/79,3*100 =
115,6%
Тпр = 115,6 – 100 = 15,6%
– в июле по сравнению с
апрелем:
Тр = 98,7/91,7*100 =
107,6%
Тпр = 107,6 – 100 = 7,6%
3) долгосрочных кредитных
вложений:
– в апреле по сравнению с
январем:
Тр = 14,3/4,3*100 =
332,5%
Тпр = 332,5 – 100 =
232,5%
– в июле по сравнению с
апрелем:
Тр = 14,2/14,3*100 =
99,3%
Тпр = 99,3 – 100 = -0,7%
Чтобы оценить изменение
структуры кредитных вложений, вычисляют линейный и квадратический коэффициенты
структурных сдвигов.
Линейный коэффициент абсолютных
структурных сдвигов определяется по формуле:
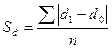 ,
(38)
,
(38)
где d1,d0 – удельные веса отдельных элементов структуры в
рассматриваемом и предыдущем периоде;
n – число выделяемых элементов
совокупности.
Квадратический
коэффициент абсолютных структурных сдвигов определяется по формуле:
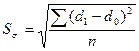 (39)
(39)
Линейный и квадратический
коэффициенты абсолютных структурных сдвигов показывают, на сколько процентных
пунктов в среднем отклоняются друг от друга сравниваемые удельные веса. При
отсутствии сдвигов в структуре совокупности эти показатели = 0. Чем больше
изменения структуры, тем выше значения коэффициентов.
Определим линейные
коэффициенты абсолютных структурных сдвигов:
– январь-апрель:
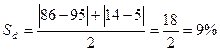
– апрель-июль:
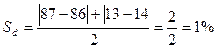
Определим квадратические
коэффициенты абсолютных структурных сдвигов:
– январь-апрель:
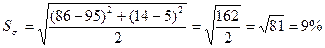
– апрель-июль:
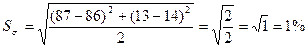
По результатам расчетов
можно сделать следующий вывод:
Удельные веса
краткосрочных и долгосрочных кредитных вложений в апреле по сравнению с январем
(на начало месяца) отклоняются друг от друга на 9%. Структура кредитных
вложений в июле по сравнению с апрелем практически не изменилась.
Наибольший удельный вес в
структуре кредитных вложений имеют краткосрочные вложения.
СПИСОК ЛИТЕРАТУРЫ
1. Голуб Л.А.
Социально-экономическая статистика. – М.: Финансы и статистика, 2003. – 265 с.
2. Гусаров В.М. Теория статистики.
– М.: ЮНИТИ, 1998. – 448 с.
3. Курс
социально-экономической статистики: Учебник для ВУЗов / под редакцией
М.Г.Назарова. – М.:ЮНИТИ-ДАНА, 2000. – 771 с.
4. Теория статистики /
Под редакцией Шмойловой Р. А. – М.: Финансы и статистика, 2002. – 576 с.
5. Экономическая
статистика: Учебник / под редакцией Ю.Н. Иванова. – М.: ИНФРА-М, 1998. – 480 с.