Министерство
образования и науки РФ
Федеральное агентство по образованию
Государственное
образовательное учреждение
Высшее
профессиональное образование
Всероссийский
заочный финансово-экономический институт
филиал в г. Туле
КОНТРОЛЬНАЯ РАБОТА
по дисциплине
СТАТИСТИКА
Вариант №10
|
Выполнил:
|
Якимов А.А.
|
курс
|
3(2)
|
факультет
|
ФК
|
|
специальность
|
Финансовый менеджмент
|
группа
|
дневная
|
|
№ зачётной
книжки
|
06ффд61409
|
|
Руководитель:
|
проф.
Мелихов Б.М.
|
Тула, 2007г.
ЗАДАНИЕ
Имеются следующие
выборочные данные о деятельности российских банков за год (выборка 3%
механическая), млн. руб.
Таблица 1
|
Номер банка
|
Кредиты
|
Прибыль
|
|
1
|
7500,00
|
150,00
|
|
2
|
6000,00
|
120,00
|
|
3
|
4600,00
|
140,00
|
|
4
|
8400,00
|
180,00
|
|
5
|
7700,00
|
280,00
|
|
6
|
10600,00
|
290,00
|
|
7
|
5700,00
|
160,00
|
|
8
|
8200,00
|
180,00
|
|
9
|
11100,00
|
280,00
|
|
10
|
7800,00
|
120,00
|
|
11
|
3400,00
|
70,00
|
|
12
|
7600,00
|
210,00
|
|
13
|
9000,00
|
250,00
|
|
14
|
11200,00
|
190,00
|
|
15
|
13400,00
|
290,00
|
|
16
|
7900,00
|
150,00
|
|
17
|
5500,00
|
100,00
|
|
18
|
3800,00
|
50,00
|
|
19
|
8500,00
|
170,00
|
|
20
|
10000,00
|
220,00
|
|
21
|
12300,00
|
350,00
|
|
22
|
9600,00
|
200,00
|
|
23
|
6800,00
|
200,00
|
|
24
|
9200,00
|
260,00
|
|
25
|
11500,00
|
220,00
|
|
26
|
8000,00
|
220,00
|
|
27
|
5200,00
|
80,00
|
|
28
|
7000,00
|
180,00
|
|
29
|
8600,00
|
210,00
|
|
30
|
9900,00
|
240,00
|
ЗАДАНИЕ 1
По исходным данным:
1.
Постройте
статистический ряд распределения банков по признаку кредиты, образовав пять групп с равными интервалами.
2.
Постойте
графики полученного ряда распределения, графически определите значение моды и
медианы.
3.
Рассчитайте
характеристики интервального ряда распределения: среднюю арифметическую,
среднее квадратическое отклонение, коэффициент вариации, моду и медиану.
4.
Вычислите
среднюю арифметическую по исходным данным, сравните ее с аналогичным
показателем, рассчитанным в п.3 для интервального ряда распределения. Объясните
причину их расхождения.
Сделайте выводы по результатам выполнения задания.
ЗАДАНИЕ2
По
исходным данным:
1. Установите наличие и характер связи
между признаками – кредиты и прибыль методами:
а)
аналитической группировки;
б)
корреляционной таблицы.
2. Измерьте тесноту корреляционной
связи между названными признаками с использованием коэффициентов детерминации и
эмпирического корреляционного отношения.
ЗАДАНИЕ 3
По результатам выполнения задания 1 с
вероятностью 0,954 определите:
1.
Ошибку выборки средней величины кредита банка и границы, в которых она будет находиться в
генеральной совокупности.
2.
Ошибку выборки доли банков с размером кредита 9400 и более млн. руб. и границы, в которых
будет находиться
генеральная доля.
ЗАДАНИЕ 4
Имеются
следующие данные о кредитовании банком промышленных предприятий, млн. руб.:
Таблица 2
|
Вид продукции
|
Средние остатки кредитов
|
Погашение кредитов
|
|
Базисный период
|
отчетный период
|
Базисный период
|
отчетный период
|
|
1
|
150
|
170
|
750
|
1190
|
|
2
|
130
|
135
|
715
|
720
|
Определите:
1.
По каждому предприятию и двум предприятиям вместе за каждый год:
—
однодневный оборот по погашению;
— длительность пользования кредитом.
2.
Индексы длительности пользования кредитом по каждому предприятию.
Рассчитанные показатели представьте в
таблице.
3.
Индексы средней длительности пользования кредитом переменного,
постоянного состава, структурных сдвигов.
Задание 1
Имеются следующие
выборочные данные о российских банков за год (выборка 3% механическая), млн.
руб.
Таблица 3
|
Номер банка
|
Кредиты
|
Прибыль
|
|
1
|
7500,00
|
150,00
|
|
2
|
6000,00
|
120,00
|
|
3
|
4600,00
|
140,00
|
|
4
|
8400,00
|
180,00
|
|
5
|
7700,00
|
280,00
|
|
6
|
10600,00
|
290,00
|
|
7
|
5700,00
|
160,00
|
|
8
|
8200,00
|
180,00
|
|
9
|
11100,00
|
280,00
|
|
10
|
7800,00
|
120,00
|
|
11
|
3400,00
|
70,00
|
|
12
|
7600,00
|
210,00
|
|
13
|
9000,00
|
250,00
|
|
14
|
11200,00
|
190,00
|
|
15
|
13400,00
|
290,00
|
|
16
|
7900,00
|
150,00
|
|
17
|
5500,00
|
100,00
|
|
18
|
3800,00
|
50,00
|
|
19
|
8500,00
|
170,00
|
|
20
|
10000,00
|
220,00
|
|
21
|
12300,00
|
350,00
|
|
22
|
9600,00
|
200,00
|
|
23
|
6800,00
|
200,00
|
|
24
|
9200,00
|
260,00
|
|
25
|
11500,00
|
220,00
|
|
26
|
8000,00
|
220,00
|
|
27
|
5200,00
|
80,00
|
|
28
|
7000,00
|
180,00
|
|
29
|
8600,00
|
210,00
|
|
30
|
9900,00
|
240,00
|

Рисунок 1
Как видно из рисунка в данной выборке
имеются аномальные единицы, необходимо убрать их, что бы выборка была более
однородна.
Таблица 4
|
Номер банка
|
Кредиты
|
Прибыль
|
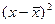
|
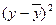
|
|
1
|
7500,00
|
150,00
|
139931,4129
|
856,1042524
|
|
2
|
6000,00
|
120,00
|
3512153,635
|
3511,659808
|
|
3
|
4600,00
|
140,00
|
10719561,04
|
1541,289438
|
|
4
|
8400,00
|
180,00
|
276598,0796
|
0,548696845
|
|
6
|
10600,00
|
290,00
|
7430672,154
|
12263,51166
|
|
7
|
5700,00
|
160,00
|
4726598,08
|
370,9190672
|
|
8
|
8200,00
|
180,00
|
106227,7092
|
0,548696845
|
|
9
|
11100,00
|
280,00
|
10406598,08
|
10148,69684
|
|
10
|
7800,00
|
120,00
|
5486,96845
|
3511,659808
|
|
11
|
3400,00
|
70,00
|
20017338,82
|
11937,58573
|
|
12
|
7600,00
|
210,00
|
75116,59808
|
944,9931413
|
|
13
|
9000,00
|
250,00
|
1267709,191
|
5004,252401
|
|
14
|
11200,00
|
190,00
|
11061783,26
|
115,3635117
|
|
16
|
7900,00
|
150,00
|
672,1536351
|
856,1042524
|
|
17
|
5500,00
|
100,00
|
5636227,709
|
6282,030178
|
|
18
|
3800,00
|
50,00
|
16598079,56
|
16707,9561
|
|
19
|
8500,00
|
170,00
|
391783,2647
|
85,73388203
|
|
20
|
10000,00
|
220,00
|
4519561,043
|
1659,807956
|
|
22
|
9600,00
|
200,00
|
2978820,302
|
430,1783265
|
|
23
|
6800,00
|
200,00
|
1153635,117
|
430,1783265
|
|
24
|
9200,00
|
260,00
|
1758079,561
|
6519,067215
|
|
25
|
11500,00
|
220,00
|
13147338,82
|
1659,807956
|
|
26
|
8000,00
|
220,00
|
15857,33882
|
1659,807956
|
|
27
|
5200,00
|
80,00
|
7150672,154
|
9852,400549
|
|
28
|
7000,00
|
180,00
|
764005,487
|
0,548696845
|
|
29
|
8600,00
|
210,00
|
526968,4499
|
944,9931413
|
|
30
|
9900,00
|
240,00
|
4104375,857
|
3689,437586
|
|
|
|
Таблица
5
|
|
Аномальные единицы наблюдения
|
|
|
Номер банка
|
Кредиты
|
Прибыль
|
|
21
|
12300,00
|
350,00
|
|
15
|
13400,00
|
290,00
|
|
5
|
7700,00
|
280,00
|
Рисунок 2
Итак, после того как мы убрали несколько наиболее аномальных
единиц, выборка стала более однородной,
это видно на рисунке 2.
По заданию число групп должно быть пять. Значит можно
построить размер интервала по выручки от продажи.
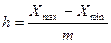 , где
, где
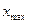 – наибольшее значение признака,
– наибольшее значение признака, 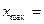 11500 млн.руб.,
11500 млн.руб.,
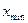 – наименьшее значение признака,
– наименьшее значение признака, 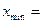 3400 млн.руб.,
3400 млн.руб.,
m – количество интервалов,
m=5;
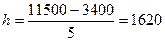
Таблица
6
Интервальный ряд распределения предприятий
по выручке от продажи
|
|
Группы банков по кредитам, млн. руб.
|
Число банков в группе
|
Накопленная частость группы
|
|
3400-5020
|
3
|
11,11%
|
|
5020-6640
|
3
|
11,11%
|
|
6640-8260
|
9
|
33,33%
|
|
8260-9880
|
6
|
22,22%
|
|
9880-11500
|
6
|
22,22%
|
|
|
|
|
|
Итого
|
27
|
100,00%
|
Итак, число групп 5, наибольшее число банков
находиться в 3 группе 6640-8260 млн. руб.
Проведем расчет предельной ошибки
выборки, использовав для этого режим Описательная статистика. Для общей выборки
уровень надежности равен 95,4 %, для предельных уровней ошибок 68,3 % и 99,7%.
|
|
|
|
Таблица 7
|
|
|
|
|
|
|
Кредиты
|
|
Прибыль
|
|
|
Среднее
|
7874,074074
|
Среднее
|
179,2592593
|
|
Стандартная
ошибка
|
427,8280332
|
Стандартная
ошибка
|
11,99389595
|
|
Медиана
|
8000
|
Медиана
|
180
|
|
Мода
|
7450
|
Мода
|
180
|
|
Стандартное
отклонение
|
2223,059671
|
Стандартное
отклонение
|
62,32211152
|
|
Дисперсия
выборки
|
4941994,302
|
Дисперсия
выборки
|
3884,045584
|
|
Эксцесс
|
-0,560990631
|
Эксцесс
|
-0,386621919
|
|
Асимметричность
|
-0,29376478
|
Асимметричность
|
-0,293367989
|
|
Интервал
|
8100
|
Интервал
|
240
|
|
Минимум
|
3400
|
Минимум
|
50
|
|
Максимум
|
11500
|
Максимум
|
290
|
|
Сумма
|
212600
|
Сумма
|
4840
|
|
Счет
|
27
|
Счет
|
27
|
|
Уровень
надежности(95,4%)
|
896,5674898
|
Уровень
надежности(95,4%)
|
25,13471852
|
|
|
|
|
Таблица 7а
|
|
Предельные ошибки выборки
|
|
|
|
|
Кредиты
|
|
Прибыль
|
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Уровень
надежности(68,3%)
|
2308,6361
|
Уровень
надежности(68,3%)
|
28,90525508
|
|
|
|
|
Таблица 7б
|
|
Предельные ошибки выборки
|
|
|
|
|
Кредиты
|
|
Прибыль
|
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Уровень
надежности(99,7%)
|
31802,45374
|
Уровень
надежности(99,7%)
|
398,1823025
|
|
|
|
|
|
|
Для получения выборочных показателей совокупности
воспользуемся соответствующими статистическими функциями инструмента Мастер функций. Данные
занесем в следующую таблицу 8.
|
|
|
|
|
Таблица 8
|
|
Выборочные
показатели вариации и асимметрии
|
|
|
Кредиты
|
|
Прибыль
|
|
Стандартное
отклонение
|
2181,50349
|
Стандартное
отклонение
|
61,15710951
|
|
Дисперсия
|
4758957,476
|
Дисперсия
|
3740,192044
|
|
Среднее
линейное отклонение
|
1747,325103
|
Среднее
линейное отклонение
|
49,0260631
|
|
Коэффициент
вариации, %
|
27,7048891
|
Коэффициент
вариации, %
|
34,11656936
|
|
Коэффициент
асимметрии
|
0,194395322
|
Коэффициент
асимметрии
|
-0,012112095
|
|
|
|
|
|
|
|
|
Таблица 9
|
|
Входная информация для построения
Гистограммы
|
|
|
Группы банков по кредитам, млн. руб.
|
Число банков в группе
|
Накопленная частость группы
|
|
5020
|
3
|
11,11%
|
|
6640
|
3
|
11,11%
|
|
8260
|
9
|
33,33%
|
|
9800
|
6
|
22,22%
|
|
11500
|
6
|
22,22%
|
|
|
|
|
|
Итого
|
27
|
100,00%
|
|
|
|
|
|
|
|
Таблица 10
|
|
Интервальный ряд распределения
предприятий
по банкам
|
|
Группы банков по кредитам, млн. руб.
|
Число банков в группе
|
Накопленная частость группы
|
|
3400-5020
|
3
|
11,11%
|
|
5020-6640
|
3
|
11,11%
|
|
6640-8260
|
9
|
33,33%
|
|
8260-9880
|
6
|
22,22%
|
|
9880-11500
|
6
|
22,22%
|
|
|
|
|
|
Итого
|
27
|
100,00%
|
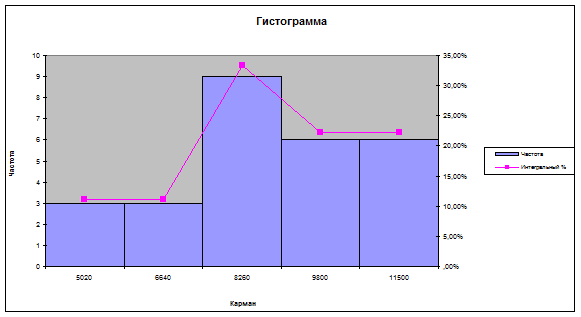 Диаграмма
1
Диаграмма
1
Среднюю арифметическую по исходным данным
вычислим как среднюю арифметическую простую:
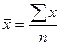 .
.
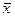 = 7874,10 млн. руб. (Для интервального
ряда
= 7874,10 млн. руб. (Для интервального
ряда 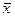 = 7874,07 млн. руб.)
= 7874,07 млн. руб.)
Вычисляя для интервального ряда, мы берем
в качестве исходной величины признака среднее значение интервала для группы,
которое не отображает надлежащим способом распределение признака по самому
интервалу. Чтобы значение средней арифметической в расчете по интервальному
ряду совпадало со значением средней арифметической, рассчитанной по исходным
данным, необходимо:
1)
вычислять
для каждого интервала свою среднюю арифметическую простую
(следовательно, надо знать все варианты признака для каждого интервала);
2)
подставлять
в расчетную формулу уже ее вместо среднего значения интервала.
Следует также учесть, что на расхождение
значений (правда, в незначительной степени), могут влиять погрешности
округления.
Выводы:
Данные
группировки показывают, что основная доля банков приходится на интервал млн. руб. На банки в этом же интервале
приходится и основная доля прибыли.
Хотя
вычисления по ряду распределения дают в целом меньшую точность результатов, чем
непосредственный расчет по исходным данным, но зато происходит экономия по
времени и затратам в сборе и обработке статистических данных. Вычислять по ряду
распределения удобно также в следующих случаях:
1) неизвестно (не может быть определено)
распределение вариантов признака по интервалам, но известно число вариант и их
распределение между интервалами;
2) требуется оценочная, не слишком
высокая точность статистического анализа (возможно предварительная).
Во втором случае некоторые показатели
(моду, медиану) можно оценить, построив гистограмму и полигон
распределения, то есть графически.
Задание 2
По исходным данным:
1. Установите наличие и
характер связи между признаками – кредиты и прибыль методами:
а) аналитической
группировки;
Составим распределение банков по кредитам
|
|
|
|
Таблица 11.
|
|
|
|
Исходные данные
|
|
|
Номер
|
Номер банка
|
кредиты (Хi)
|
прибыль (Yi)
|
|
1
|
11
|
3400,00
|
70,00
|
|
2
|
18
|
3800,00
|
50,00
|
|
3
|
3
|
4600,00
|
140,00
|
|
4
|
27
|
5200,00
|
80,00
|
|
6
|
7
|
5700,00
|
160,00
|
|
7
|
2
|
6000,00
|
120,00
|
|
8
|
23
|
6800,00
|
200,00
|
|
9
|
28
|
7000,00
|
180,00
|
|
10
|
1
|
7500,00
|
150,00
|
|
11
|
12
|
7600,00
|
210,00
|
|
12
|
5
|
7700,00
|
280,00
|
|
13
|
10
|
7800,00
|
120,00
|
|
14
|
16
|
7900,00
|
150,00
|
|
15
|
26
|
8000,00
|
220,00
|
|
16
|
8
|
8200,00
|
180,00
|
|
17
|
4
|
8400,00
|
180,00
|
|
18
|
19
|
8500,00
|
170,00
|
|
19
|
29
|
8600,00
|
210,00
|
|
20
|
13
|
9000,00
|
250,00
|
|
21
|
24
|
9200,00
|
260,00
|
|
22
|
22
|
9600,00
|
200,00
|
|
23
|
30
|
9900,00
|
240,00
|
|
24
|
20
|
10000,00
|
220,00
|
|
25
|
6
|
10600,00
|
290,00
|
|
26
|
9
|
11100,00
|
280,00
|
|
27
|
14
|
11200,00
|
190,00
|
|
28
|
25
|
11500,00
|
220,00
|
Составим таблицу
зависимости прибыли (результативного
признака 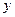 ) от кредитов (факторного признака
) от кредитов (факторного признака 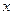 ), в которой отразим средние значения по обоим
признакам для каждой группы, вычисленные по формуле:
), в которой отразим средние значения по обоим
признакам для каждой группы, вычисленные по формуле:
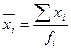 ,
, 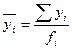 , где
, где
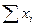 – сумма вариаций факторного признака в
– сумма вариаций факторного признака в 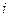 -ой группе;
-ой группе;
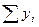 – сумма вариаций результативного признака в
– сумма вариаций результативного признака в 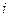 -ой группе;
-ой группе;
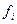 – количество банков в
– количество банков в 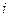 -ой группе.
-ой группе.
Таблица 12
|
Группы предприятий по кредитам
|
Количество банков
|
Кредиты млн.руб.
|
Прибыль млн.руб.
|
|
|
ср.значение
|
ср.значение
|
|
|
3400-5020
|
3
|
3933,33
|
86,67
|
|
|
|
|
|
|
|
|
|
5020-6640
|
3
|
5633,33
|
120,00
|
|
|
6640-8260
|
9
|
7611,11
|
187,78
|
|
|
|
8260-9880
|
6
|
8883,33
|
211,67
|
|
|
|
9880-11500
|
6
|
10716,67
|
240,00
|
|
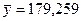
Данные полученной таблицы показывают, что с ростом
кредитных займов, прибыль также
увеличивается. Следовательно, между исследуемыми признаками существует прямая
корреляционная зависимость.
Построим корреляционную
таблицу, образовав пять групп по факторному и результативному признакам.
Для этого воспользуемся
имеющимся разбиением по факторному признаку и дополнительно построим разбиение
на пять групп по результативному признаку.
Определим длину
интервала:
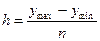 ,
,
где 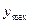 – наибольшее
значение признака,
– наибольшее
значение признака, 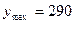 млн. руб.,
млн. руб.,
 – наименьшее значение признака,
– наименьшее значение признака, 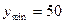 млн. руб.,
млн. руб.,
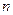 – количество интервалов,
– количество интервалов, 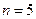 ;
;
Тогда
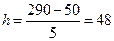 млн. руб.
млн. руб.
Получим следующий ряд
распределения:
Таблица 13
Интервальный
и дискретный статистические ряды распределения по результирующему признаку
“Прибыль”
|
№ группы
|
Интервальный
ряд (млн.руб.)
|
Дискретный ряд
(млн.руб.)
|
Число Банков
|
Число банков %
|
|
1
|
50-98
|
74
|
3
|
11,11%
|
|
2
|
98-146
|
122
|
3
|
11,11%
|
|
3
|
146-194
|
170
|
8
|
29,63%
|
|
4
|
194-242
|
218
|
8
|
29,63%
|
|
5
|
242-290
|
266
|
5
|
18,52%
|
Получим таблицу:
Таблица 14
Распределение
предприятий по основным признакам
|
|
Прибыль (млн.руб.)
|
|
|
50-98
|
98-146
|
146-194
|
194-242
|
242-290
|
ИТОГО
|
|
Кредит (млн.руб.)
|
3400-5020
|
2
|
|
1
|
|
|
3
|
|
5020-6640
|
1
|
2
|
|
|
|
3
|
|
6640-8260
|
|
1
|
4
|
3
|
1
|
9
|
|
8260-9880
|
|
|
2
|
2
|
2
|
6
|
|
9880-11500
|
|
|
1
|
3
|
2
|
6
|
|
|
3
|
3
|
8
|
8
|
5
|
27
|
Как видно из данных таблицы
14, распределение числа банков достаточно хаотично, однако все-таки
прослеживается их группировка вдоль диагонали из левого верхнего в правый
нижний угол таблицы, т.е. увеличение факторного признака сопровождается
увеличением результативного признака. Характер концентрации частот по диагонали
корреляционной таблицы свидетельствует о наличии прямой корреляционной связи
между рассматриваемыми признаками.
Теснота корреляционной
связи между названными признаками с использованием коэффициента детерминации и
эмпирического корреляционного отношения.
Коэффициент детерминации
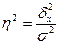 ,
,
где 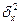 – межгрупповая
дисперсия,
– межгрупповая
дисперсия,
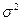 – общая дисперсия,
– общая дисперсия,
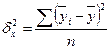 ,
,
где 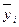 – групповая
средняя (из таблицы 5)
– групповая
средняя (из таблицы 5)
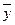 – общая средняя (из таблицы 5),
– общая средняя (из таблицы 5),
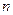 – количество интервалов,
– количество интервалов,
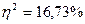
Эмпирическое
корреляционное отношение:
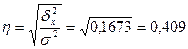
Значение коэффициента
детерминации 16,73% показывает, что
прибыль банков на 16,73% зависит
от кредитов, и лишь на 83,67% – от других причин, не связанных с
кредитами.
Эмпирическое
корреляционное отношение составляет 0,409, что свидетельствует о несущественном
влиянии на прибыль кредитов.
Задание 3
Ошибка выборки
средней выручки от продажи продукции и границы, в которых она будет
находиться в генеральной совокупности.
Ошибка выборки средней
величины работающих активов для механической 3%-ной выборки:
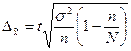
где 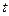 – коэффициент
доверия, для данной точности – 0,954 возьмем
– коэффициент
доверия, для данной точности – 0,954 возьмем 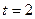 ,
,
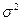 – дисперсия выборочной совокупности,
– дисперсия выборочной совокупности, 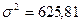
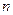 – численность выборки,
– численность выборки, 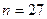
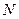 – общее количество предприятий, т.к. выборка
3%-ная, то
– общее количество предприятий, т.к. выборка
3%-ная, то 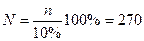
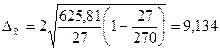 млн.руб.,
млн.руб.,
Границы, в которых будет
находиться средняя величина работающих активов в генеральной совокупности:
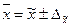
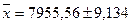 млн.руб., или
млн.руб., или 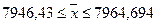 млн.руб.
млн.руб.
Ошибка
выборки доли банков с размером кредита 9400 и более млн. руб. и границы, в
которых будет находиться
генеральная доля.
Определим долю банков с размером кредита 9400 и более млн.руб. в выборке, она равна отношению
количеству банков с указанной величиной прибыли
(7 шт.) ко всему количеству предприятий в выборке (27 шт.):
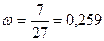
Определим предельную
ошибку выборки для доли (выборка 3%-ная механическая):
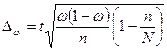 ,
,
где 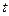 – коэффициент
доверия, необходимая точность 0,954, для нее
– коэффициент
доверия, необходимая точность 0,954, для нее 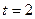 ,
,
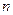 – количество банков в выборке,
– количество банков в выборке, 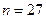 ,
,
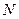 – общее количество банков, т.к. выборка
3%-ная, то
– общее количество банков, т.к. выборка
3%-ная, то 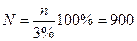
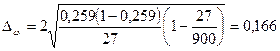
Границы, в которых будет
находиться генеральная доля:
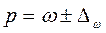 ,
,
отсюда
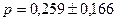 , или
, или 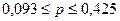 .
.
Задание
4
Имеются следующие данные о
кредитовании банком промышленных предприятий, млн. руб.:
Таблица
15
|
Вид продукции
|
Средние остатки кредитов
|
Погашение кредитов
|
|
Базисный период
|
отчетный период
|
Базисный период
|
отчетный период
|
|
1
|
150
|
170
|
750
|
1190
|
|
2
|
130
|
135
|
715
|
720
|
Определите:
1. По каждому предприятию и двум предприятиям
вместе за каждый год:
— однодневный оборот по погашению;
— длительность
пользования кредитом.
2. Индексы длительности пользования кредитом по
каждому предприятию.
Рассчитанные показатели
представьте в таблице.
3.
Индексы средней длительности
пользования кредитом переменного, постоянного состава, структурных сдвигов.
1.
По каждому предприятию и двум предприятиям вместе за каждый год:
—
однодневный оборот по погашению;
—
длительность
пользования кредитом.
Количество оборотов
кредита (n) определяется путем деления оборота ссуд по погашению на средний их
остаток:
n = Oп/K
Этот показатель
характеризует число оборотов, совершенных краткосрочным кредитом за
анализируемый период по клиентуре банковского учреждения. Число оборотов ссуд
относится к прямым характеристикам оборачиваемости кредита.
Если известна длительность
пользования кредитом, то количество оборотов ссуд можно определить, пользуясь
взаимосвязью этих показателей:
n = Д : t
Таблица 16
|
№
предприятия
|
Однодневный
оборот по погашению
|
Длительность
пользования кредитом
|
|
|
Базисный
период
|
отчетный
период
|
Базисный
период
|
отчетный
период
|
|
1
|
2,08
|
3,305
|
72,11
|
51,43
|
|
2
|
1,986
|
2
|
65,74
|
67,5
|
|
По
двум предприятиям
|
4,069
|
5,306
|
68,81
|
57,48
|
2. Индексы
длительности пользования кредитом по каждому предприятию.
Рассчитанные показатели представьте в таблице.
Таблица
17
|
№
предприятия
|
Индекс длительности
пользования кредитом
|
|
1
|
0,7132
|
|
2
|
0,874
|
|
Общий
|
0,8353
|
3. Индексы средней
длительности пользования кредитом переменного, постоянного состава, структурных
сдвигов.
Построим индекс средней длительности
пользования кредитом
переменного состава:
It = SK1/Sm1 : SK0/Sm0
где m – однодневный
оборот по погашению кредита, равный Оп : Д. Так как
t = К/m, то К = tm
Подставим вместо К его
значение в формулу индекса переменного состава:
It = St1m1/Sm1 : St0m0/Sm0 = t1 : t0,
It=57.48/68.81=0.835=83.5%
Длительность оборота
сократилась на 16,5 %. На величину индекса оказывают влияние изменения
длительности пользования кредитом определенных единиц совокупности и удельный
вес однодневного оборота по погашению отдельных частей совокупности в общей его
величине
Для того чтобы определить
влияние на прирост средней длительности пользования кредитом изменения только
первого фактора, необходимо исчислить индекс постоянного состава:
I пост = Itпер*Iстр
Определение влияния
второго фактора – структурных изменений в составе однодневного оборота по
погашению на прирост средней длительности пользования кредитом производится
путем расчета индекса влияния структуры:
Iстр = St0m1/Sm1 : St0m0/Sm0,
Iстр=(3.305*72,11+65,49*2)/(3,305+2)
: 68,81 = 1,012=101,2%
Из вычисления следует
влияние удельного веса однодневного оборота на
прирост средней длительности пользования кредитом, т.к., судя по
результатам расчета структурного индекса, произошло увеличение на 1,2 %.
Для
определения влияния на прирост средней длительности пользования кредитом
изменения только длительности пользования кредитом необходимо вычисления
индекса постоянного состава:
I пост = 1,012*0,835=0,8447=84,47%
Длительность отрицательно
влияет на прирост средней длительности
пользования кредитом снижение произошло на 15,53 %.
Итак, посмотрев
статистику по погашениям кредитов можно сказать что погашения увеличились,
произошло это, в -первую очередь, потому что,
время пользования кредитами уменьшилось, что говорит о том что
промышленные предприятия стали более платежеспособным, хотя еще и осталась
задолженность пред банками.
Список литературы.
1. Практикум
по статистике: Учебн.пособие для вузов / Под ред.В.М.Симчеры/ВЗФЭИ. М.:
«Финстатинформ»», 1999.
2. Теория
статистики: Учебн.пособие для вузов. – М.:Аудит, ЮНИТ,2001.