СОДЕРЖАНИЕ
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. 2
1. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ДВИЖЕНИЯ НАСЕЛЕНИЯ.. 2
2. СТАТИСТИЧЕСКИЕ МЕТОДЫ В ИССЛЕДОВАНИИ
ПРОИЗВОДИТЕЛЬНОСТИ ТРУДА.. 7
ПРАКТИЧЕСКАЯ ЧАСТЬ. 12
ЗАДАНИЕ 1. 12
ЗАДАНИЕ 2. 16
ЗАДАНИЕ 3. 19
ЗАДАНИЕ 4. 23
ЗАДАНИЕ 5. 27
ЗАДАНИЕ 6. 29
СПИСОК ЛИТЕРАТУРЫ.. 31
Вариант 1
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ДВИЖЕНИЯ НАСЕЛЕНИЯ
Как статистическая
категория население представляет собой совокупность людей, проживающих на
данной территории. Оно непрерывно изменяется за счет рождения и смертей.
Движение населения – это
изменение численности населения за период времени. Процесс движения населения
может приобретать одну из трех форм:
1) естественного
движения. Естественное движение – это процесс, который меняет численность
населения путем его обновления (смертность и рождаемость) или содействует этому
изменению (бракосочетания и разводы);
2) механического
движения. Механическое движение – это процесс изменения численности и
состава населения за счет его территориального перемещения (урбанизация,
миграция, иммиграция);
3) социального
движения. Социальное движение – это процесс изменения социального состава
населения вследствие его социально-экономического и культурного развития
(исчезновение одних слоев населения и появление других).
Цель статистического исследования этих процессов
заключается в оценивании их объемов, степени распространения и проявления,
определении закономерностей распределения, развития и взаимосвязи.
Изменение численности населения между переписями
отслеживается с помощью текущего учета населения, который основывается на
статистике естественного и миграционного (механического) движения населения.
Естественное движение населения – это изменение
численности населения за счет рождения и
смертей. В статистике широко используется показатель естественного прироста
населения, который определяют как разность между числом родившимися живыми и
числом умерших за определенный период, имея в виду, прежде всего, положительный
результат (число родившихся должно превышать численность умерших). Если разница
имеет отрицательный результат, то речь идет о показателе естественной убыли
населения.
Воспроизводство населения измеряется с помощью
общего коэффициента рождаемости и общего коэффициента смертности. Эти
коэффициенты рассчитываются на 1 000 человек, то есть в промилле, ‰.
Общий коэффициент рождаемости характеризует
интенсивность деторождения по отношению к населению в целом (всех возрастов) и
вычисляется как отношение числа родившимися живыми в течение года (N) к
среднегодовой численности населения (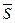 ):
):
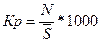 (1)
(1)
Интенсивность смертности населения измеряется
общим коэффициентом смертности, который представляет собой отношение общего
числа умерших в течение года (М) к среднегодовой численности населения (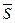 ):
):
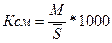 (2)
(2)
В статистике населения используется также
коэффициент естественного прироста (убыли), который представляет собой разность
между коэффициентом рождаемости и коэффициентом смертности:
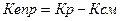 (3)
(3)
Большое значение для анализа естественного движения
населения имеет расчет возрастных коэффициентов рождаемости (коэффициентов для
отдельных возрастных групп женщин) и суммарного коэффициента рождаемости,
который характеризует среднее число детей, рожденных женщиной за свою жизнь. В
последние годы в России суммарный коэффициент рождаемости имеет тенденцию к
снижению (суммарный коэффициент рождаемости снизился с 2,00 в 1970 г. до 1,24 в 1998 г.).
Важнейшей частью статистической информации о
смертности населения является показатель смертности детей на первом году жизни.
Речь идет о коэффициенте младенческой смертности, который представляет собой
отношение числа умерших в возрасте до одного года (М0) к числу
родившимися живыми:
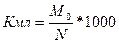 (4)
(4)
Обобщающим показателем является показатель
средней продолжительности предстоящей жизни, который может быть рассчитан для
любой возрастной группы населения путем
суммы предстоящих человеко-лет, которые предстоит прожить группе лиц от
возраста х до предельного возраста включительно (Тх), на численность
изучаемого поколения, дожившего до возраста х (Lx):
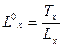 (5)
(5)
Статистическая информация свидетельствует, что
продолжительность жизни в России в последнее десятилетие уменьшилась:
Таблица 1
Продолжительность жизни в России
|
Год
|
Все население
|
Мужчины
|
Женщины
|
|
1990
|
69,20
|
63,79
|
74,27
|
|
1995
|
64,64
|
58,27
|
71,70
|
|
1998
|
67,02
|
61,30
|
72,93
|
Кроме естественного движения большое влияние на
численность населения страны оказывает перемещение населения по территории
страны – миграция населения. Изменение численности населения на отдельных
территориях за счет миграции представляет собой механическое движение
населения.
Миграция населения – это передвижение людей
(мигрантов) через границы тех или иных территорий (страны, региона, области,
района и т. д.), связанное с переменой места жительства навсегда или на более
или менее длительное время. Маятниковая миграция – систематическое передвижение
из города в город (учеба и т.п.).
Миграционные потоки являются важным объектом
исследования, поскольку дают сведения о том, как перемещается население, в
каком направлении, что из себя представляет социально-демографический состав
мигрантов.
К основным показателя миграции относятся
следующие:
• число прибытий – П;
• число выбытий – В;
• миграционный прирост – (П – В), если П > В;
• миграционный отток – (П – В), если П < В.
Выбывшим считается лицо, которое выехало за
пределы данной территории. К прибывшим относятся лица, которые въехали на
данную территорию из-за ее пределов. Число выбывших и прибывших определяется по
показателям регистрационных учетов по месту прибытия и месту убытия.
Для статистической характеристики миграционных
процессов используют расчетные относительные показатели: коэффициенты
интенсивности (прибытия, выбытия, миграционного оборота), коэффициент
эффективности миграции.
Коэффициент прибытия характеризует число
прибывших на 1000 человек населения в среднем за год и определяется по формуле:
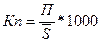 , (6)
, (6)
где П – число прибывших.
Коэффициент выбытия характеризует число выбывших
на 1000 человек населения в среднем за год и определяется по формуле:
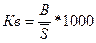 , (7)
, (7)
где В – число выбывших.
Коэффициент интенсивности миграционного оборота
рассчитывается следующим образом:
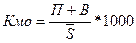 (8)
(8)
Данный коэффициент может иметь как положительное
значение (+), так и отрицательное (-) и характеризует в положительном значении
приток, а в отрицательном – отток.
Коэффициент миграционного механического прироста
определяется по формуле:
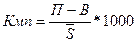 (9)
(9)
Наконец, важным показателем является коэффициент
эффективности миграции, который определяется по формуле:
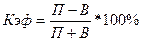 (10)
(10)
2. СТАТИСТИЧЕСКИЕ МЕТОДЫ В ИССЛЕДОВАНИИ
ПРОИЗВОДИТЕЛЬНОСТИ ТРУДА
Важнейшим
аспектом статистического анализа являются измерение уровня и динамики
производительности труда, исследование факторов, влияющих на рост
производительности труда.
Производительность труда
будучи сложной экономической категорией измеряется несколькими показателями,
находящимися между собой в определенных отношениях и соотношениях. Среди этих
показателей первостепенную роль играют соотношение показателей объема, величин
полученных благ от применения соответствующего количества труда.
Уровень производительности труда можно измерить двумя показателями:
1. Прямым показателем
– средней выработкой продукции в единицу времени.
2. Обратным показателем
– трудоемкостью единицы продукции.
Средняя выработка (W) продукции в единицу времени определяется как отношение объема
произведенной продукции (Q) к затратам труда (Т) (затратам рабочего времени):
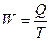 (11)
(11)
Трудоемкость
(t) единицы продукции является показателем, обратным производительности труда,
и измеряется как отношение затрат рабочего времени (Т) к объему произведенной
продукции (Q):
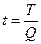 (12)
(12)
При
исчислении уровня производительности труда следует иметь в виду, что и
числитель, и знаменатель в данной формуле могут быть выражены в различных
единицах. Числитель данного уравнения отражает объем
произведенной продукции. Существуют натуральный, стоимостной (денежный) и
трудовой методы измерения объема продукции.
В
соответствии с принятыми методами определения объема произведенной продукции
различают следующие методы измерения производительности труда:
1.
Натуральный и его разновидности на основе условно-натуральных измерителей
продукции;
2.
Трудовой и его разновидности на основе нормированного и фактически
отработанного времени;
3.
Стоимостный и его разновидности на основе показателей объема продукции (валовой
и товарной) и объема (чистой, условной чистой, нормативно чистой продукции,
нормативной стоимости обработки, нормативной заработной платы).
Сущность метода
натурального измерения производительности труда состоит в том, что количество
выработанной продукции в натуральном выражении, измеренное в физических
единицах меры, длины, массы и т.д., выражают в затратах времени на ее
изготовление. Чаще всего эти затраты представляются в отработанных
человеко-часах, человеко-днях.
Но наиболее
универсальным является стоимостный метод измерения производительности труда, в
основу которого положен способ сопоставления объема продукции в денежном
выражении с затратами живого труда. Он дает возможность измерять уровень
производительности труда при производстве разнородной продукции, а также
обеспечивает получение сводных данных как по отраслям и регионам, так и по экономике
в целом.
В знаменателе
данной формулы рассматриваются затраты труда на производство продукции в
единицу времени.
Затраты труда могут быть выражены в:
а)
человеко-часах;
б)
человеко-днях;
в)
человеко-месяцах, человеко-кварталах, человеко-годах.
Это позволяет
различать показатели уровня производительности труда:
• среднечасовую выработку Wчас, характеризующую средний объем
продукции, произведенной одним рабочим за один час фактически отработанного
времени;
• среднедневную выработку Wдн, характеризующую средний объем
продукции, произведенной одним рабочим за один день фактически отработанного
времени;
• среднемесячную, среднеквартальную, среднегодовую выработку продукции (соответственно
за один месяц, квартал, год фактически отработанного времени).
Для изучения динамики производительности труда в статистическом исследовании
используются индексы производительности труда iW
.
Если
исследуется производство однородной продукции, то
исчисляются индивидуальные индексы следующими методами:
1)
сопоставлением прямых показателей производительности труда:
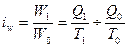 (13)
(13)
2)
сопоставлением обратных показателей (трудоемкости):
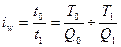 (14)
(14)
Для базисного
и отчетного периодов зависимость динамики объема продукции от затрат рабочего
времени и производительности труда можно выразить так:
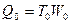 и
и 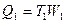 (15)
(15)
При этом общий прирост продукции за счет обоих факторов составит:
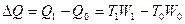 (16)
(16)
В условиях
рыночной конкуренции большинство предприятий старается ориентироваться на
выпуск разнородной продукции. В этом случае исчисляется общий индекс производительности труда. Здесь могут быть
использованы следующие подходы:
1.
Сопоставление прямых показателей, когда в зависимости от выбора соответствующих
единиц выражения продукции рассчитанный общий индекс может быть:
а) трудовым индексом производительности труда, где общий объем
разнородной продукции выражен в нормо-часах рабочего времени (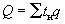 ):
):
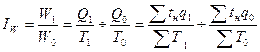 (17)
(17)
б) стоимостным индексом производительности труда, где общий объем
разнородной продукции представлен в денежном выражении (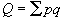 ).
Подставляя в предыдущую формулу соответствующее выражение Q, получаем
стоимостный индекс производительности труда:
).
Подставляя в предыдущую формулу соответствующее выражение Q, получаем
стоимостный индекс производительности труда:
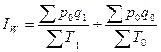 (18)
(18)
2. Сопоставление индексов объема продукции и
затрат труда:
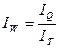 ,
(19)
,
(19)
где IQ – индекс физического объема
произведенной продукции,
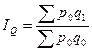 ;
;
IT – индекс затрат труда, 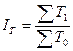
3.
Использование данных о трудоемкости различных видов продукции для сравнения
величин, характеризующих:
а) затраты
рабочего времени на продукцию отчетного периода при базисных уровнях
производительности труда;
б)
фактические затраты рабочего времени на продукцию отчетного периода.
Известно, что
соотношение этих данных характеризует трудовой индекс
постоянного состава:
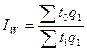 (20)
(20)
Если из
фактических затрат рабочего времени на продукцию отчетного периода
(знаменатель) вычесть затраты рабочего времени на продукцию отчетного периода
при базисных условиях производительности труда (числитель), то данная величина
будет характеризовать экономию (дополнительные затраты) рабочего времени в
зависимости от роста (снижения) производительности труда:
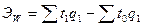 (21)
(21)
ПРАКТИЧЕСКАЯ ЧАСТЬ
ЗАДАНИЕ 1
С целью нахождения
зависимости между экономическими показателями провести группировку 30
предприятий машиностроения, распределив их в 5 групп с равными интервалами.
Согласно варианта 1
рассматриваются предприятия с 1 по 30, группировочным признаком является число
рабочих, результативным – чистая прибыль.
Таблица 1
Основные финансово-экономические
показатели предприятий машиностроения
|
№ предприятия
|
Число рабочих в смену, чел.
|
Чистая прибыль, млн. руб.
|
№ предприятия
|
Число рабочих в смену, чел.
|
Чистая прибыль, млн. руб.
|
|
1
|
25
|
15,1
|
16
|
36
|
18,3
|
|
2
|
24
|
13,6
|
17
|
40
|
16,7
|
|
3
|
43
|
15,4
|
18
|
30
|
13,1
|
|
4
|
41
|
16,7
|
19
|
35
|
16,8
|
|
5
|
37
|
18,8
|
20
|
25
|
16,0
|
|
6
|
42
|
19,6
|
21
|
39
|
14,0
|
|
7
|
29
|
17,4
|
22
|
53
|
19,0
|
|
8
|
38
|
20,3
|
23
|
27
|
14,3
|
|
9
|
50
|
21,5
|
24
|
26
|
15,6
|
|
10
|
29
|
17,8
|
25
|
19
|
13,5
|
|
11
|
18
|
12,1
|
26
|
40
|
17,5
|
|
12
|
25
|
15,0
|
27
|
21
|
18,0
|
|
13
|
30
|
16,3
|
28
|
27
|
13,6
|
|
14
|
37
|
15,8
|
29
|
18
|
13,1
|
|
15
|
26
|
15,2
|
30
|
22
|
14,3
|
Решение
Группировка – это
расчленение совокупности на однородные группы единиц по какому-либо
существенному признаку.
При построении группировки необходимо решить вопросы
выбора группировочного признака, числа группы и интервала.
Интервал – это
значение варьируемого признака, отделяющего одну группу от другой.
В общем случае, если распределение единиц в
совокупности по интересующему признаку достаточно равномерно, допускается
использование следующей формулы для расчета равных интервалов:
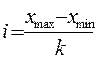 , (1)
, (1)
где i – шаг интервала,
хmax,
хmin – максимальное и минимальное значения признака,
K – число групп.
Группировочным признаком в нашем случае является число рабочих.
Определим шаг интервала:
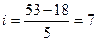 чел.
чел.
Отсюда получаем следующие интервалы:
Таблица 2
|
№ группы
|
Граница интервала (значение, чел.)
|
|
|
Нижняя (минимальное)
|
Верхняя (максимальное)
|
|
1
|
18
|
18 + 7 = 25
|
|
2
|
25
|
25 + 7 = 32
|
|
3
|
32
|
32 + 7 = 39
|
|
4
|
39
|
39 + 7 = 46
|
|
5
|
46
|
46 + 7 = 53
|
Отсюда распределим 30 предприятий по группам в зависимости числа рабочих
в смену:
Таблица 3
Группировка
предприятий по числу рабочих в смену
|
Группы предприятий по числу рабочих в смену, чел.
|
№ предприятия
|
Число рабочих в смену, чел.
|
Чистая прибыль, млн. руб.
|
|
18 – 25
|
1
|
25
|
15,1
|
|
2
|
24
|
13,6
|
|
11
|
18
|
12,1
|
|
12
|
25
|
15,0
|
|
20
|
25
|
16,0
|
|
25
|
19
|
13,5
|
|
27
|
21
|
18,0
|
|
29
|
18
|
13,1
|
|
30
|
22
|
14,3
|
|
25 – 32
|
7
|
29
|
17,4
|
|
10
|
29
|
17,8
|
|
13
|
30
|
16,3
|
|
15
|
26
|
15,2
|
|
18
|
30
|
13,1
|
|
23
|
27
|
14,3
|
|
24
|
26
|
15,6
|
|
28
|
27
|
13,6
|
|
32 – 39
|
5
|
37
|
18,8
|
|
8
|
38
|
20,3
|
|
14
|
37
|
15,8
|
|
16
|
36
|
18,3
|
|
19
|
35
|
16,8
|
|
21
|
39
|
14,0
|
|
39 – 46
|
3
|
43
|
15,4
|
|
4
|
41
|
16,7
|
|
6
|
42
|
19,6
|
|
17
|
40
|
16,7
|
|
26
|
40
|
17,5
|
|
46 – 53
|
9
|
50
|
21,5
|
|
22
|
53
|
19,0
|
Результаты
распределения (группировки) занесем в следующую таблицу.
Таблица 4
Группировка предприятий по числу рабочих в смену
|
Группы предприятий по числу рабочих в смену, чел.
|
Число предприятий
|
Число рабочих в смену, чел.
|
Чистая прибыль, млн. руб.
|
|
всего
|
На 1 предприятие
|
всего
|
На 1 предприятие
|
|
18 – 25
|
9
|
197
|
22
|
130,7
|
14,522
|
|
25 – 32
|
8
|
224
|
28
|
123,3
|
15,412
|
|
32 – 39
|
6
|
222
|
37
|
104,0
|
17,333
|
|
39 – 46
|
5
|
206
|
41
|
85,9
|
17,180
|
|
46 – 53
|
2
|
103
|
51
|
40,5
|
20,250
|
|
Итого
|
30
|
952
|
–
|
484,4
|
–
|
Таким образом, судя по значениям 1, 4, 6 граф можно
предположить наличие достаточно тесной связи между данными показателями, причем,
чем больше число рабочих в смену, тем выше чистая прибыль предприятия.
ЗАДАНИЕ 2
Рассчитать по результатам
1-го задания:
1) структуру совокупности
предприятия по группировочному признаку;
2) среднее значение
группировочного признака;
3) коэффициент вариации.
Сформулировать выводы.
Решение
Относительный
показатель структуры характеризует удельный вес (долю) структурного элемента во
всей совокупности и рассчитывается как отношение части и целого.
Средний
показатель – это обобщающая характеристика совокупности по какому-либо
варьирующему признаку. Наиболее распространенная форма средней – средняя
арифметическая.
Формула средней
арифметической простой выглядит следующим образом:
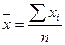 (2)
(2)
Формула средней
арифметической взвешенной выглядит следующим образом:
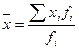 ,
(3)
,
(3)
где 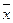 – среднее значение признака;
– среднее значение признака;
х – индивидуальное значение признака;
n – численность совокупности;
f – частота повторения xi значения признака.
Формула (2) используется для
несгруппированной информации, формула (3) – для сгруппированной.
Коэффициент вариации –
относительный показатель, характеризующий вариацию признака. Он показывает, на
сколько процентов в среднем отличаются индивидуальные значения признака от
среднего уровня и рассчитывается следующим образом:
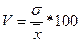 ,
(4)
,
(4)
где V – коэффициент вариации,
s –
среднее квадратическое отклонение.
Среднее квадратическое
отклонение показывает, на сколько в среднем колеблется величина признака у единиц исследуемой совокупности и определяется в
зависимости от характера исходных данных.
При
расчете по исходным данным используем формулу:
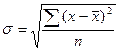 (5)
(5)
По сгруппированным
данным:
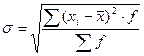 (6)
(6)
Группировочным признаком
является число рабочих.
Рассчитаем относительные
показатели структуры. Результаты сведем в таблицу 5.
Таблица 5
Распределение предприятий по числу
рабочих в смену
|
Группы предприятий по числу рабочих в смену, чел.
|
Средние интервалы, чел.
|
Число предприятий
|
|
Число
|
В % к итогу
|
|
18 – 25
|
21,5
|
9
|
30,0
|
|
25 – 32
|
28,5
|
8
|
26,7
|
|
32 – 39
|
35,5
|
6
|
20,0
|
|
39 – 46
|
42,5
|
5
|
16,7
|
|
46 – 53
|
49,5
|
2
|
6,6
|
|
Итого
|
–
|
30
|
100,0
|
В четвертой графе
представлены относительные показатели структуры.
Определим среднее число
рабочих в смену:
– для несгруппированных
данных по формуле (2):
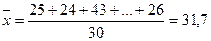 чел.
чел.
– для сгруппированных
данных по формуле (3):
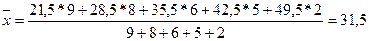 чел.
чел.
где значения 21,5; 28,5;
35,5; 42,5 и 49,5 – середины соответствующих интервалов (графа 2 таблицы 5).
В первом случае значение
более точно.
Определим среднее
квадратическое отклонение:
– для несгруппированных
данных по формуле (5):
 чел.
чел.
– для сгруппированных
данных по формуле (6):
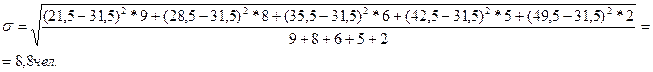 Определим коэффициент
вариации по формуле (4):
Определим коэффициент
вариации по формуле (4):
– для несгруппированных
данных:
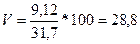 %
%
– для сгруппированных
данных:
 %
%
Если V> 33,3%, то совокупность в общем
случае считается неоднородной по данному признаку.
Сделаем вывод по
значениям, полученным по несгруппированной информации: в основной части предприятий
(30%) число рабочих в смену составляет от 18 до 25 человек. Среднее же число
рабочих в смену составляет 32 человека. Причем число рабочих в смену отличается
от этого уровня в среднем на 9 лет или на 28,1%. Таким образом, совокупность предприятий
по числу рабочих в смену неоднородна.
ЗАДАНИЕ 3
Для определения среднего
размера вклада проведено 5%-ное обследование в случайном бесповторном порядке и
получено следующее распределение вкладов.
|
Размер вклада, тыс. руб.
|
Число вкладов
|
|
До 1,0
|
15
|
|
1,0 – 3,0
|
30
|
|
3,0 – 5,0
|
45
|
|
5,0 – 10,0
|
81
|
|
10 и более
|
39
|
|
Итого
|
210
|
Определите с вероятностью
0,954:
1) пределы средней
величины вклада;
2) пределы доли вкладов,
размер которых менее 3 тысяч рублей.
Решение
Границы средней в
генеральной совокупности определяются:
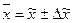 (7)
(7)
или
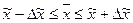 ,
(8)
,
(8)
где 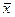 – средняя в генеральной совокупности,
– средняя в генеральной совокупности,
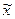 – средняя в выборочной совокупности,
– средняя в выборочной совокупности,
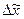 – предельная ошибка выборочной средней.
– предельная ошибка выборочной средней.
Предельная ошибка
выборочной средней определяется по формуле:
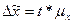 ,
(9)
,
(9)
где t – коэффициент доверия, при уровне
вероятности 0,954 t = 2,0;
μх – средняя ошибка
выборочной средней.
Для механической и
бесповторной случайной выборок средняя ошибка выборочной средней определяется
по формуле:
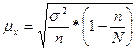 ,
(10)
,
(10)
где s2 – показатель вариации признака
(дисперсия);
n – численность выборочной
совокупности;
N – численность генеральной
совокупности;
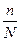 – доля отбора.
– доля отбора.
Границы
генеральной доли определяются:
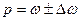 (11)
(11)
или
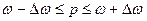 ,
(12)
,
(12)
где р – генеральная доля (удельный
вес единиц генеральной совокупности, обладающих данным признаком), выражается в
коэффициентах или в процентах;
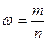 ,
(13)
,
(13)
где m – число единиц в выборочной
совокупности, обладающих данным признаком;
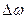 – предельная ошибка
доли.
– предельная ошибка
доли.
Предельная ошибка доли
рассчитывается по формуле:
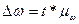 ,
(14)
,
(14)
где 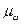 – средняя ошибка доли.
– средняя ошибка доли.
Для механической и
случайной бесповторной выборок средняя ошибка доли определяется по формуле:
 , (15)
, (15)
1) Определим среднюю величину вклада по формуле
(3).
Для расчета средней
величины вклада необходимо варианты признака выразить одним числом
(дискретным). За такое дискретное число принимается средняя арифметическая
простая из верхнего и нижнего значения интервала.
Например, для второй
группы: (1,0+3,0)/2 = 2,0 тыс. руб.
Так как первый и
последний интервал является открытыми, то величина интервала первой группы принимается
равной величине интервала последующей (2,0), а величина интервала последней
группы – величине интервала предыдущей группы (5,0). Таким образом, условно
принимаем:
1 группа: 0 – 1,0
5 группа: 10,0 – 15,0
Определим средние
величины интервалов:
1 группа: 0,5 тыс. руб.
2 группа: 2,0 тыс. руб.
3 группа: 4,0 тыс. руб.
4 группа: 7,5 тыс. руб.
5 группа: 12,5 тыс. руб.
Тогда средняя величина
вклада составит:
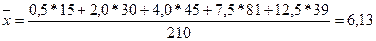 тыс. руб.
тыс. руб.
Определим дисперсию по
формуле:
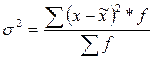
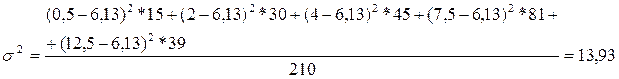
N = 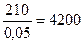
Определим среднюю ошибку
выборочной средней по формуле (10):
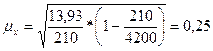
Определим предельную
ошибку выборочной средней по формуле (9):
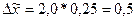
Определим границы средней
в генеральной совокупности по формуле (8):
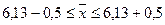
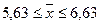
Пределы средней величины
вклада с вероятностью 0,954 составляют от 5,63 тыс. руб. до 6,63 тыс. рублей.
2) Число вкладов менее 3
тысяч рублей составляет 45 (30+15).
Определим долю по формуле
(13):
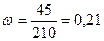 , то есть 21% в совокупности это вклады менее 3 тыс. рублей
, то есть 21% в совокупности это вклады менее 3 тыс. рублей
N = 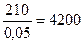
Определим среднюю ошибку
доли по формуле (15):
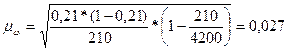
Определим предельную ошибку
доли по формуле (14):
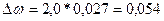
Определим
границы генеральной доли по формуле (12):
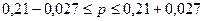
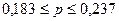
С вероятностью 0,954 доля
вкладов менее 3 тысяч рублей находится в пределах от 18,3% до 23,7%.
ЗАДАНИЕ 4
Имеются следующие данные
по Сахалинской области за 1995–1999 гг.
|
Показатель
|
1995
|
1996
|
1997
|
1998
|
1999
|
|
Среднегодовая численность
трудовых ресурсов, тыс. чел.
|
445,1
|
444,9
|
404,2
|
395,6
|
395,3
|
На основе приведенной
информации для анализа динамики за 1995 – 1999 гг. определите:
1) показатели изменения
уровней ряда динамики (абсолютный прирост, темпы роста и прироста)
– цепные;
– базисные (к начальному
уровню);
2) абсолютное содержание
одного процента прироста;
3) среднегодовой уровень;
4) среднегодовые
абсолютный прирост, темпы роста и прироста.
Изобразите графически
динамику исследуемого показателя. Представьте результаты 1 и 2 заданий в
табличной форме.
Решение
Для количественной оценки
динамики социально-экономических явлений применяются показатели, представленные
в таблице 6.
Таблица 6
Основные
динамические показатели динамики и их расчет
|
Показатель
|
Базисный
|
Цепной
|
|
Абсолютный прирост (Di)
|
Dбi = yi – yo
|
Dцi = yi – yi-1
|
|
Темп роста
(Трi)
|
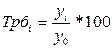
|
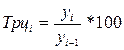
|
|
Темп прироста
(Тпрi)
|
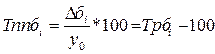
|
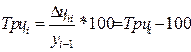
|
|
Абсолютное значение одного
процента прироста
(Аi)
|

(как правило, не определяется)
|
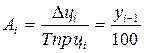
|
В таблице 6 y0 – уровень, принятый за постоянную базу сравнения;
yi – сравниваемый уровень.
Результаты расчетов показателей динамики, перечисленных в
таблице 4, представим в следующей таблице.
Таблица 7
Аналитические показатели динамики среднегодовой численности трудовых
ресурсов в Сахалинской области за 1995–1999 гг.
|
Годы
|
1995
|
1996
|
1997
|
1998
|
1999
|
|
Среднегодовая численность
трудовых ресурсов, тыс. чел.
|
445,1
|
444,9
|
404,2
|
395,6
|
395,3
|
|
Абсолютный прирост, млн.
тонн
-
цепной
-
базисный
|
-
-
|
-0,2
-0,2
|
-40,7
-40,9
|
-8,6
-49,5
|
-0,3
-49,8
|
|
Темпы
роста, %
-
цепной
-
базисный
|
-
-
|
99,9
99,9
|
90,85
90,81
|
97,9
88,9
|
99,9
88,8
|
|
Темпы
прироста, %
-
цепной
-
базисный
|
-
-
|
-0,1
-0,1
|
-9,15
-9,19
|
-2,1
-11,1
|
-0,1
-11,2
|
|
Абсолютное содержание
одного процента прироста
|
-
|
4,451
|
4,449
|
4,042
|
3,956
|
Средний уровень ряда
динамики определяется следующим образом:
а) для интервальных
полных рядов динамики:
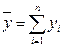 ,
(16)
,
(16)
где n – число уровней yi
б) для моментальных
полных рядов динамики:
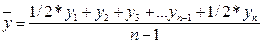 (17)
(17)
в) для неполных
интервальных (моментных) рядов динамики:
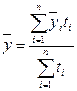 ,
(18)
,
(18)
где 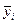 – средний уровень ряда динамики, сохранившийся без изменения в
течение промежутка времени ti.
– средний уровень ряда динамики, сохранившийся без изменения в
течение промежутка времени ti.
ti – период времени, для которого
рассчитан 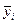 .
.
Средний абсолютный
прирост определяется по формуле:
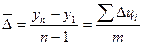 ,
(19)
,
(19)
где m – число полных абсолютных приростов.
Средний темп роста
определяется по формуле:
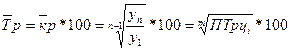 ,
(20)
,
(20)
где 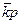 – средний коэффициент
роста;
– средний коэффициент
роста;
m – число цепных коэффициентов роста.
Средний темп прироста
определяется:
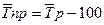 (21)
(21)
Среднегодовой уровень за 1995–1999
годы определим по формуле (16):
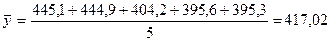 тыс. чел.
тыс. чел.
Среднеаналитические показатели
рассчитаем по формулам (19), (20), (21):
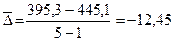 тыс. чел.
тыс. чел.
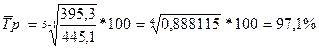
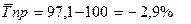
Таким образом, в среднем за год среднегодовая численность
трудовых ресурсов снижалась на 12,45 тыс. человек, или на 2,9%. Причем, с
наибольшим темпом снижение произошло в 1997 и в 1998 годах (по сравнению с
предыдущими периодами). В 1999 году ситуация улучшилась, но все равно имеется
незначительное снижение.
Изобразим графически с
помощью диаграммы динамику среднегодовой численности трудовых ресурсов в
Сахалинской области за 1995–1999 гг. (рис.1).
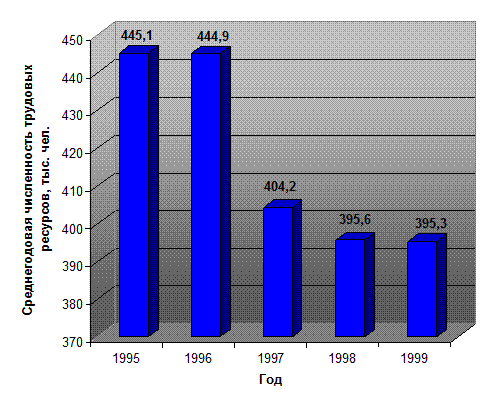
Рис. 1 Динамика среднегодовой
численности трудовых ресурсов в Сахалинской области за 1995–1999 гг.
ЗАДАНИЕ 5
Имеются следующие данные
о расходе материала на производство 3-х видов продукции и объемах их выпуска за
два года:
|
Вид продукции
|
Расход материала, тыс. кг
|
Выпуск продукции, штук
|
|
базисный
|
отчетный
|
базисный
|
отчетный
|
|
А
|
4,5
|
4,3
|
1200
|
1100
|
|
Б
|
8,1
|
9,0
|
4100
|
4200
|
|
В
|
4,0
|
4,4
|
800
|
950
|
Определить:
1) индексы удельного
расхода материала по каждому виду продукции;
2) индекс удельного
расхода материала в целом по трем видам продукции и размер экономии
(перерасхода) материала в результате изменения удельного расхода.
Сформулируйте выводы.
Решение
1) Индексы удельного
расхода материала по каждому виду продукции можно определить по следующей
формуле:
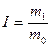 ,
(22)
,
(22)
где m1, m0 – удельный расход материалов соответственно в отчетном и
базисном периодах.
Определим индексы
удельного расхода материала по каждому виду продукции:
– по продукции «А»:
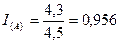 , или 95,6%
, или 95,6%
– по продукции «Б»:
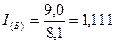 , или 111,1%
, или 111,1%
– по продукции «В»:
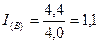 , или 110%
, или 110%
2) Индекс удельного
расхода материала в целом по трем видам продукции определяется по формуле:
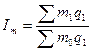 , (23)
, (23)
где q1 – количество выпущенной продукции в отчетном периоде.
Индекс удельного расхода
материала в целом по трем видам продукции составит:
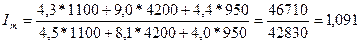 , или 109,1%
, или 109,1%
Размер экономии
(перерасхода) материала в результате изменения удельного расхода определяется
как разница между числителем и знаменателем индекса удельного расхода материала
в целом по трем видам продукции:
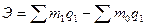 (24)
(24)
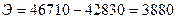 тыс. кг
тыс. кг
По результатам расчетов
сделаем следующие выводы:
В отчетном периоде по
сравнению с базисным удельный расход материала на продукцию «А» снизился на 4,4%, а на продукцию «Б» и «В»
увеличился соответственно на 11,1% и 10%. Удельный расход материала в целом по
трем видам продукции увеличился на 9,1%, вследствие этого наблюдался перерасход
материала на 3880 тыс. кг.
ЗАДАНИЕ 6
Рассчитать коэффициент
корреляции между результативным и факторным признакам по исходным Задания 1
Вашего варианта.
Решение
Факторным признаком
является число рабочих, результативным – чистая прибыль.
Распространенной
характеристикой тесноты связи является коэффициент корреляции. Между двумя
признаками тесноты связи можно оценить с помощью парного коэффициента
корреляции:
 , (25)
, (25)
где 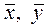 – средние значения
признаков,
– средние значения
признаков,
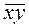 – средняя из произведений
индивидуальных значений признаков,
– средняя из произведений
индивидуальных значений признаков,
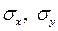 – среднеквадратические отклонения
признаков.
– среднеквадратические отклонения
признаков.
Считается, что связь
тесная, при r ³ 0,8, слабая при 0,5 < r < 0,8, отсутствует при r < 0,5.
Определим средние
значения признаков по формуле (2):
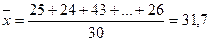 чел.
чел.
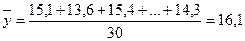 млн. руб.
млн. руб.
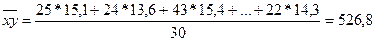
Определим среднее квадратическое
отклонение по формуле (5):
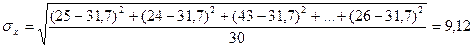 чел.
чел.
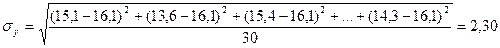 млн. руб.
млн. руб.
Теперь определим коэффициент
корреляции по формуле (25):
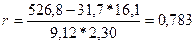
Рассчитанный коэффициент корреляции ≈ 0,8, следовательно, между числом
рабочих в смену и чистой прибылью имеется достаточно тесная связь.
СПИСОК ЛИТЕРАТУРЫ
1. Голуб Л.А.
Социально-экономическая статистика. – М.: Финансы и статистика, 2003. – 265 с.
2. Гусаров В.М. Теория
статистики. – М.: ЮНИТИ, 1998. – 448 с.
3. Давыдова Л. А. Теория
статистики в вопросах и ответах: Учебное пособие. – М.: Издательство ТК Велби,
2005. – 160 с.
4. Ефимова М. Р., Петрова
Е.В., Румянцев В.Н. Общая теория статистики. – М.: ИНФРА-М. 2002. – 416 с.
5. Курс
социально-экономической статистики: Учебник для ВУЗов / под редакцией
М.Г.Назарова. – М.:ЮНИТИ-ДАНА, 2000. – 771 с.
6. Теория статистики /
Под редакцией Шмойловой Р. А. – М.: Финансы и статистика, 2002. – 576 с.
7. Экономическая
статистика: Учебник / под редакцией Ю.Н. Иванова. – М.: ИНФРА-М, 1998. – 480 с.