Министерство образования и науки РФ

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Всероссийский заочный финансово-экономический институт

Филиал в г. Туле

Лабораторная  работа

по дисциплине «Эконометрика»

на тему

«Временной ряд. Регрессионный и корреляционный анализ»

Выполнили: студенты 3-го курса

факультета Финансово-кредитного

специальности финансы и кредит

группы вечерней

Проверил: Давыдова Т.Ю.

Тула 2007 г.

Задача 1.

         Динамика численности населения Тульской области характеризуется данными (тыс. чел.), представленными в табл.1.

Таблица 1

Годы, x

Все население,  тыс. чел. y

1979

1907,6

1980

1903,4

1989

1861,4

1990

1856,2

1991

1849,3

1992

1838,7

1993

1834,1

1994

1826,6

1995

1819,8

1996

1809,7

1997

1796,6

1998

1782,1

1999

1766,0

2000

1743,4

2001

1719,7

2002

1675,8

2003

1669,8

2004

1644,8

2005

1621,9

2006

1599,8

Требуется:

1.     Провести расчет параметров линейного и экспоненциального трендов.

2.     Построить графики рядов динамики и тренда.

3.     Выбрать наилучший вид тренда на основании графического изображения и значения коэффициента детерминации.

Произведем решение с использованием ППП MS Excel.

1.Расчет параметров линейного и экспоненциального трендов.

         1.1. Встроенная статистическая функция ЛИНЕЙН определяет параметры линейной регрессии 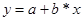. Порядок вычисления:

- в ячейки А2:В22 вводим исходные данные;

- выделяем область пустых ячеек Е3:F7 для вывода результатов регрессионной статистики;

- активизируем Мастер функций: на панели инструментов Стандартная щелкаем по кнопке Вставка функции;

- в окне Категория (рис.1.1) выбираем Статистические, в окне Функция – ЛИНЕЙН. Щелкаем ОК.

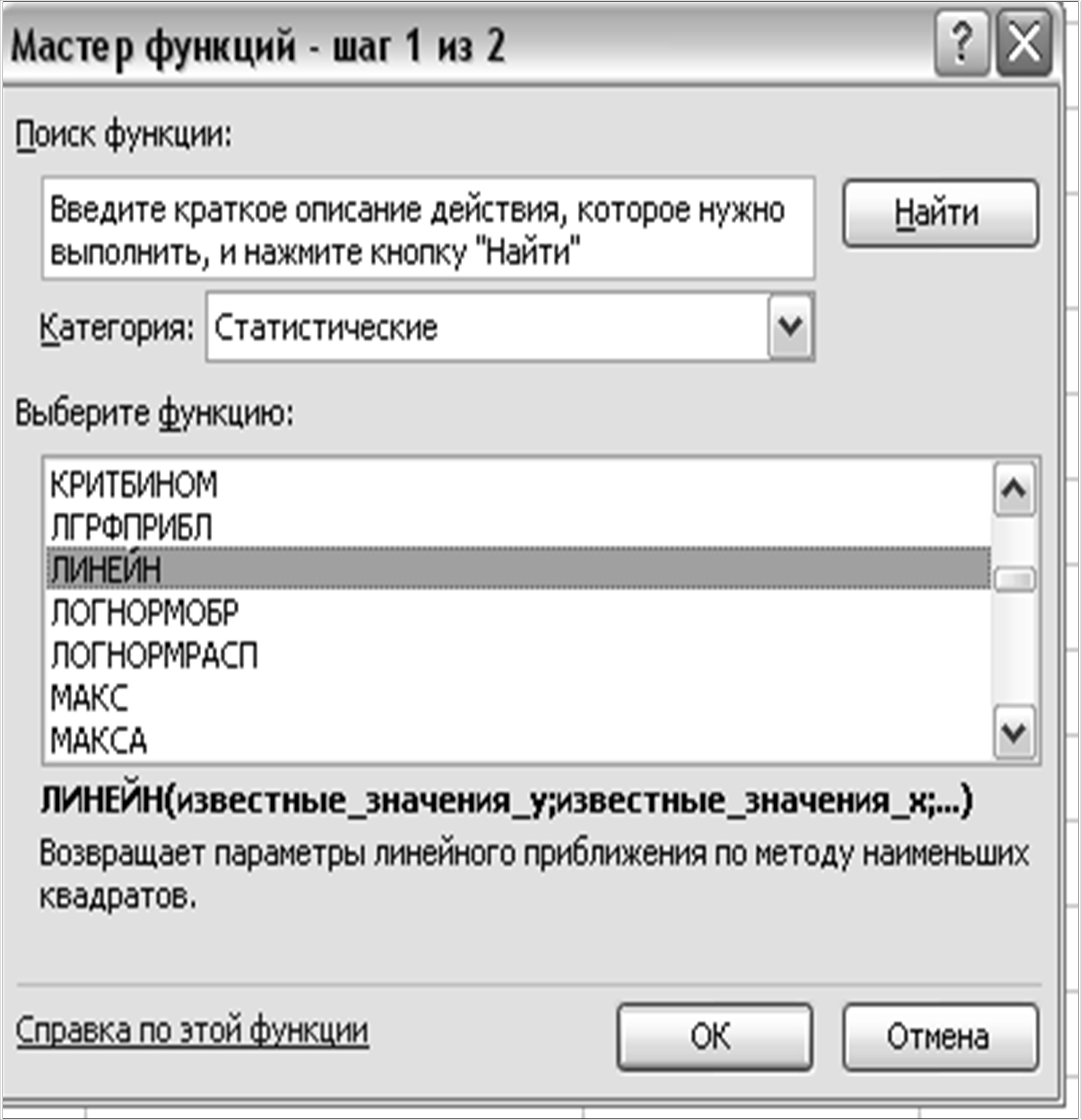
Рис. 1.1. Диалоговое окно «Мастер функций»

- заполняем аргументы функции (рис 1.2.):

·       Известные_значения_y – диапазон В3:В22

·       Известные_значения_x – диапазон А3:А22

·       Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа=1, то свободный член рассчитывается обычным образом.

·       Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика =1, то дополнительная информация выводится.

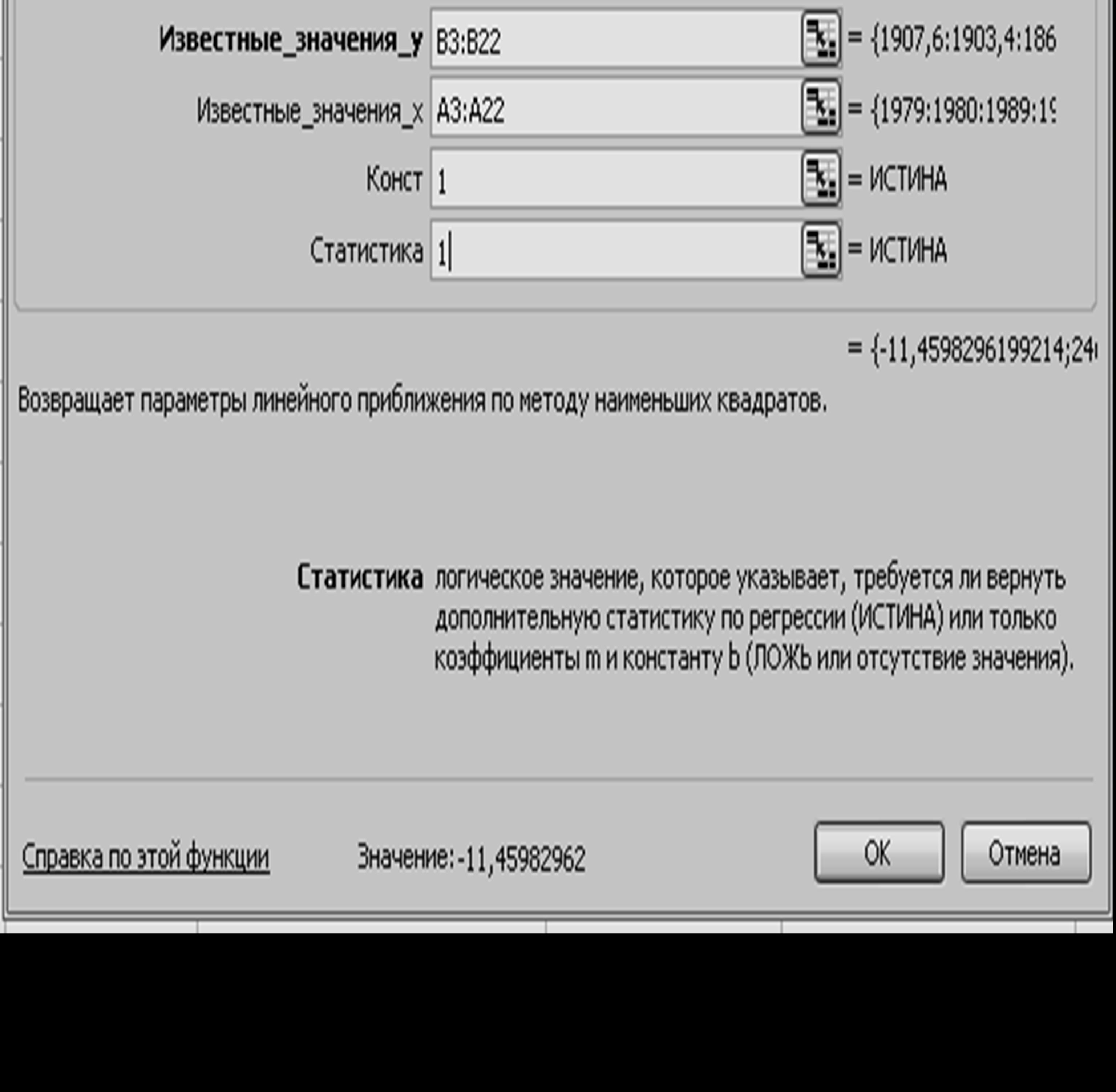
Рис. 1.2. Диалоговое окно ввода аргументов функции ЛИНЕЙН

- в ячейке Е3 выделенной области появляется первый элемент итоговой таблицы. чтобы раскрыть всю таблицу, нажимаем на клавишу <F2>, а затем на комбинацию клавиш  <CTRL>+<SHIFT>+<ENTER>.

         1.2. Для вычисления параметров экспоненциальной кривой 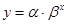 в MS Excel применяется встроенная функция ЛГРФПРИБЛ. Порядок вычисления аналогичен применению функции ЛИНЕЙН.

         Результаты вычисления функции ЛИНЕЙН и функции ЛГРФПРИБЛ представлены на рис. 1.3.

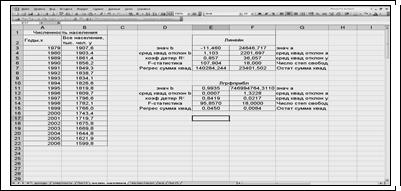
Рис. 1.3. Результаты вычисления функции ЛИНЕЙН и функции ЛГРФПРИБЛ

Запишем уравнения линейного и экспоненциального тренда, используя данные рис. 1.3.:

,

.

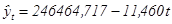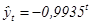         2. Построение графиков осуществляется с помощью Мастера диаграмм.

Порядок построения:

1) активизируем Мастер диаграмм: на панели инструментов Стандартная щелкаем по кнопке Мастер диаграмм;

2) в окне Тип выбираем График (рис. 1.4); вид графика выбираем в поле рядом со списком типов. Щелкаем Далее;

Рис. 1.4.Диалоговое окно Мастера диаграмм: тип диаграммы

3) заполняем диапазон данных А2:В22. Установим флажок размещения данных в столбцах (рис.1.5). Щелкнуть Далее;

Рис. 1.5. Диалоговое окно Мастера диаграмм: источник данных

4) заполним параметры диаграммы на разных закладках (рис.1.6): названия диаграммы и осей, значения осей, линии сетки, параметры легенды, таблица и подписи данных. Щелкаем Далее;

Рис. 1.6. Диалоговое окно Мастера диаграмм: параметры диаграммы

5) укажем место размещения диаграммы на имеющемся листе (рис.1.7). Готовая диаграмма, отражающая динамику уровней изучаемого ряда, представлена на рис. 1.8.

Рис. 1.7. Диалоговое окно Мастера диаграмм: размещение диаграммы

Рис.1.8. Динамика численности населения

            В ППП MS Excel  линия тренда может быть добавлена в график. Для этого:

1) выделяем область построения диаграммы; в главном меню выбираем Диаграмма/Добавить линию тренда;

2) в появившемся диалоговом окне (рис.1.9) выберите вид линии тренда и задаем параметры. Для полиномиального тренда задаем степень аппроксимирующего полинома - 6.

Рис. 1.9. Диалоговое окно типов линий тренда

На диаграмме отображаем уравнение регрессии и значение коэффициента детерминации, установив соответствующие флажки на закладке Параметры (рис.1.10). Щелкнем ОК.

         На рис. 1.11 – 1.15. представлены различные виды трендов, описывающие исходные данные задачи.

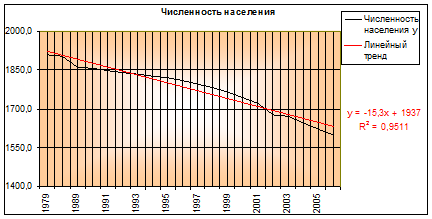
Рис. 1.11. Линейный тренд

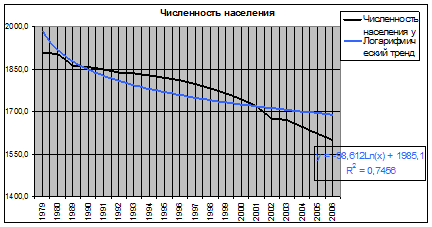
Рис. 1.12. Логарифмический тренд

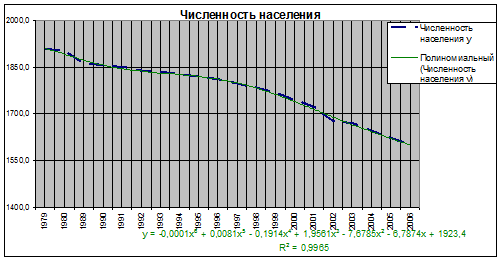
Рис. 1.13. Полиномиальный тренд

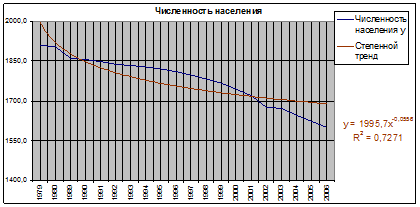
Рис. 1.14. Степенной тренд

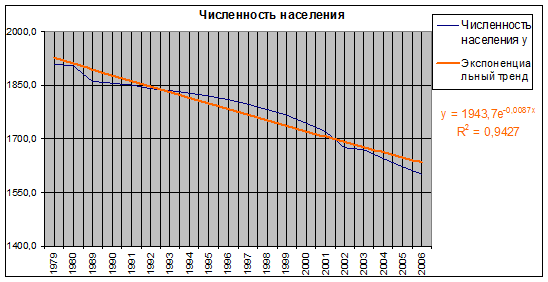
Рис. 1.15. Экспоненциальный тренд

            3. Сравним значения 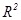по разным уравнениям трендов:

Полиномиальный тренд 6 степени -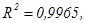

Линейный тренд -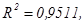

Экспоненциальный тренд -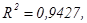

Логарифмический тренд -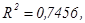

Степенной тренд -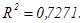

         Исходные данные лучше всего описывает полином 6-й степени. Следовательно, для расчета прогнозных значений следует использовать полиномиальное уравнение. Задача 2.

            По 6 годам с 2000 по 2005 изучается зависимость общей площади жилых помещений, приходящаяся в среднем на одного жителя Тульской области  y (м²) от среднемесячной номинальной начисленной заработной платы работников организаций по видам экономической деятельности (руб.):  финансовая деятельность - х1, образование - х2 (табл.2).

Жилищные условия населения

Среднемесячная номинальная начисленная заработная плата работников организаций по видам экономической деятельности (руб)

Год

Площадь жилищ, приходящаяся в среднем на одного жителя, м2

финансовая деятельность

образование

 

y

x1

x2

2000

19,2

3892

939

2001

19,5

7419

1448

2002

19,8

10499

2393

2003

20,2

11941

2758

2004

20,5

12472

3462

2005

20,9

15586

4267

Требуется:

1. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения МНК для их изучения.

2. Проанализировать линейные коэффициенты парной и частной корреляции.

3. Написать уравнение множественной регрессии, оценить значи­мость его параметров, пояснить их экономический смысл.

4. С помощью F-критерия Фишера оценить статистическую надеж­ность уравнения регрессии и 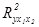. Сравнить значения скорректи­рованного и нескорректированного линейных коэффициентов мно­жественной детерминации.

5. Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на ре­зультат.

         Решение с помощью ППП Excel.

         1. Сводную таблицу основных статистических характеристик для одного или нескольких массивов данных можно получить с помо­щью инструмента анализа данных Описательная статистика. Для этого выполняем следующие шаги:

1) введите исходные данные -  ячейки А1:Е9.

2) в главном меню выбираем последовательно пункты Сервис/Анализ данных / Описательная статистика, после чего щелкните по кнопке ОК;

3) заполним диалоговое окно ввода данных и параметров вывода (рис. 2.1):

Входной интервал - диапазон, содержащий анализируемые дан­ные: В3:D9.

Группирование - по столбцам;

Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Выходной интервал – указываем ячейку B18.

Результаты вычисления соответствующих показателей для каждого признака представлены на рис. 2.2.

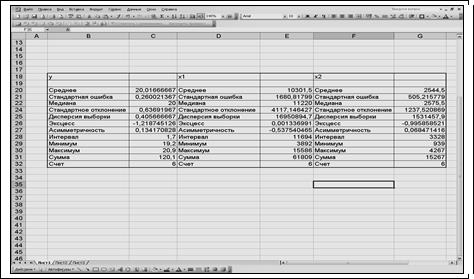
Рис. 2.2. Результат применения инструмента Описательная статистика

            Сравнивая значения средних квадратических отклонений и сред­них величин и определяя коэффициенты вариации:

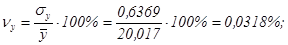
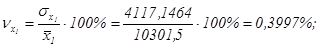
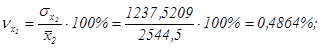
приходим к выводу о пониженном уровне варьирования признаков, в допустимых пределах, не превышающих 35%. Совокуп­ность однородна, и для ее изучения могут использо­ваться метод наименьших квадратов и вероятностные методы оцен­ки статистических гипотез.

         2. Значения линейных коэффициентов парной корреляции опреде­ляют тесноту попарно связанных переменных, использованных в данном уравнении множественной регрессии. Линейные коэффици­енты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представ­ленных в уравнении множественной регрессии.

         К сожалению, в ППП MS Excel нет специального инструмента для расчета линейных коэффициентов частной корреляции. Матрицу парных коэффициентов корреляции переменных можно рассчитать, используя инструмент анализа данных Корреляция. Для этого:

1) в главном меню последовательно выбираем пункты  Сервис / Анализ данных / Корреляция. Щелкните по кнопке ОК;

2) заполняем диалоговое окно ввода данных и параметров вывода (см. рис. 2.3);

Рис.2.3. Диалоговое окно ввода параметров инструмента Описательная статистика

3) результаты вычислений - матрица коэффициентов парной корре­ляции - представлены на рис. 2.4.

 

y

x1

x2

y

1

 

 

x1

0,96850787

1

 

x2

0,993312136

0,976052755

1

Рис. 2.4. Матрица коэффициентов парной корреляции

            Значения коэффициентов парной корреляции указывают на весьма тесную связь общей площади жилых помещений, приходящаяся в среднем на одного жителя Тульской области  y как со среднемесячной номинальной начисленной заработной платы работников финансовых организаций - х1 (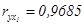), так и работников образовательных учреждений – х2(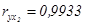). Но в то же время межфакторная связь   весьма тесная и превышает тесноту связи х1 с y. В связи с этим для улучшения данной модели можно исключить из нее фактор х1 как малоинформативный, недостаточно статистически надежный. 

         3. Вычисление параметров  линейного уравнения множественной регрессии.

         Эта операция проводится с помощью инструмента анализа дан­ных Регрессия.

1) в главном меню выбираем Сервис/Анализ данных/Регрессия.

Щелкните по кнопке ОК;

2) заполните диалоговое окно ввода данных и параметров выво­да (рис. 2.5):

Входной интервал Y - диапазон, содержащий данные результа­тивного признака В3:В9;

Входной интервал X - диапазон, содержащий данные факторов независимого признака С3:D9;

Метки - флажок, который указывает, содержит ли первая строка названия столбцов или нет;

Константа - ноль - флажок, указывающий на наличие или от­сутствие свободного члена в уравнении;

Выходной интервал – В35.

Результаты анализа представлены на рис. 2.6.

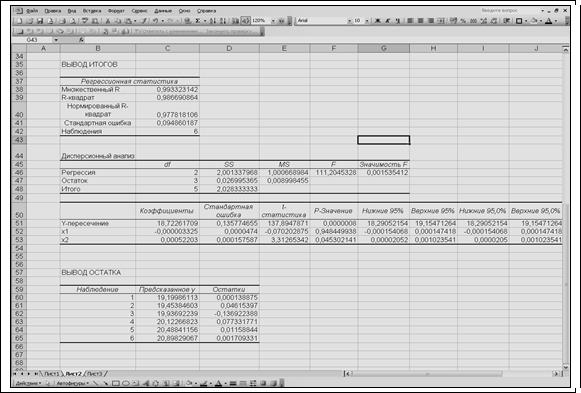
Рис. 2.6. Результат применения инструмента Регрессия

По результатам вычислений составим уравнение множественной регрессии вида ;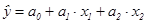

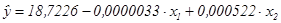
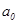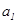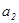Значения случайных ошибок , и с учетом округления:

   

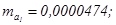
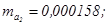
         Они показывают, какое значение данной характеристики сфор­мировалось под влиянием случайных факторов. Эти значения ис­пользуются для расчета t-критерия Стьюдента:

  

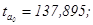
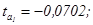
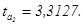
         Если значения t-критерия больше 2-3, можно сделать вывод о существенности данного параметра, который формируется под воз­действием неслучайных причин. Здесь статистически значимыми являются 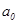 и 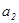, а величина 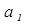сформировалась под воздействием случайных причин.

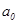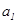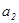         Величина  оценивает агрегированное влияние прочих (кроме учтенных в модели факторов x1 и х2) факторов на результат у. Величина   указывает, что с увеличением х1 на едини­цу его значений результат уменьшается на 0,0000033 м². Величина  указывает, что с увеличением х2 на едини­цу его значений результат увеличивается на 0,000522 м². Сравнивать эти значения не следует, так как они зависят от единиц измерения каждого признака и потому несопоста­вимы между собой.

4. Оценку надежности уравнения регрессии в целом и показателя тесноты связи 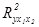 дает F-критерий Фишера:

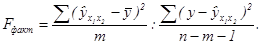
         По данным таблицы дисперсионного анализа, представленной на рис. 2.6, 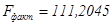  . Вероятность случайно получить такое значение F-критерия составляет 0,0015, что не превышает до­пустимый уровень значимости 5%; об этом свидетельствует величи­на Р — значения из этой же таблицы. Следовательно, полученное зна­чение не случайно, оно сформировалось под влиянием существен­ных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи .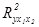

         Значения скорректированного и нескорректированного линей­ных коэффициентов множественной детерминации приведены на рис. 2.6 в рамках регрессионной статистики.

         Нескорректированный коэффициент множественной детерминации      оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 98,67% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами - на весьма тесную связь факторов с результатом.

         Скорректированный коэффициент множественной детерминации 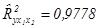 определяет тесноту связи с учетом степеней сво­боды общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 90%) де­терминированность результата у в модели факторами х1 и х2.

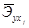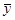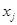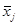         5. Средние частные коэффициенты эластичности  показыва­ют, на сколько процентов от значения своей средней  изменяется результат при изменении фактора на 1% от своей средней ,  и при фиксированном воздействии на у всех прочих факторов, вклю­ченных в уравнение регрессии. Для линейной зависимости

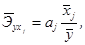
где 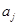 - коэффициент рецессии при xj в уравнении множественной регрессии. Здесь

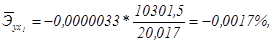
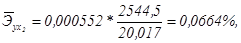
         По значениям частных коэффициентов эластичности можно сде­лать вывод о более сильном влиянии на результат у признака факто­ра х2, чем признака фактора х1: 0,0664% против -0,0017%.