Оглавление
Задача 1. 2
Задача 2. 4
Задача 1
Численные методы решения нелинейных алгебраических уравнений
с одной переменной.
Уравнение f(x) = 0 имеет вид 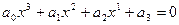
Исследовать интервалы изоляции корней данного уравнения,
найти тремя методами:
1.
Метод деления отрезка пополам.
2.
Метод простой итерации.
3.
Метод Ньютона.
Приблизительное
значение корня в интервале [α;b] и сравнить результаты. а0
= 1, а1 = -8, а2 = 0, а3 = 6, α = 0,2, b = 1,2
Решение
Учитывая
приведенные в условии значения коэффициентов уравнение примет вид: 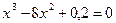
|
α n
|
b n
|
g n=(α n+b n)/2
|
f (α n)
|
f (g n)
|
D = ½α n-b n½
|
|
0,2
|
1,2
|
0,7
|
-0,112
|
-3,377
|
1
|
|
0,2
|
0,7
|
0,45
|
-0,112
|
-1,328875
|
0,5
|
|
0,2
|
0,45
|
0,325
|
-0,112
|
-0,61067188
|
0,25
|
|
0,325
|
0,45
|
0,3875
|
-0,610671875
|
-0,94306445
|
0,125
|
|
0,325
|
0,3875
|
0,35625
|
-0,610671875
|
-0,77009937
|
0,0625
|
|
0,325
|
0,35625
|
0,340625
|
-0,610671875
|
-0,68868198
|
0,03125
|
|
0,340625
|
0,35625
|
0,3484375
|
-0,688681976
|
-0,72896619
|
0,015625
|
|
0,340625
|
0,3484375
|
0,34453125
|
-0,688681976
|
-0,70871778
|
0,0078125
|
|
0,340625
|
0,34453125
|
0,342578125
|
-0,688681976
|
-0,69867328
|
0,00390625
|
|
0,34257813
|
0,34453125
|
0,343554688
|
-0,698673283
|
-0,70368889
|
0,001953125
|
|
0,34257813
|
0,34355469
|
0,343066407
|
-0,698673283
|
-0,70117942
|
0,000976563
|
|
0,34257813
|
0,34066407
|
0,341621098
|
-0,698673283
|
-0,69377091
|
0,001914055
|
|
0,3416211
|
0,34066407
|
0,341142584
|
-0,693770915
|
-0,69132452
|
0,000957028
|
|
0,3416211
|
0,34114258
|
0,341381841
|
-0,693770915
|
-0,69254732
|
0,000478514
|
|
0,3416211
|
0,34138184
|
0,34150147
|
-0,693770915
|
-0,69315902
|
0,000239257
|
|
0,34150147
|
0,34138184
|
0,341441656
|
-0,693159019
|
-0,69285314
|
0,000119629
|
|
0,34150147
|
0,34144166
|
0,341471563
|
-0,693159019
|
-0,69300608
|
5,9814E-05
|
Проверка: 0,3414715633 – 8* 0,3414715632 + 0,2 =
-0,693159019.
Ответ искомое значение корня уравнения 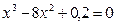 в интервале [0,2; 1,2], полученное методом деления отрезка
пополам, после выполнения шестнадцати итераций хn = 0,3414715633.
в интервале [0,2; 1,2], полученное методом деления отрезка
пополам, после выполнения шестнадцати итераций хn = 0,3414715633.
Для применения метода простой
итерации приведем уравнение 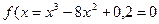 к виду
к виду 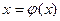 так, чтобы на всем отрезке [x0, x0+d] = [0,1] выполнилось равенство
так, чтобы на всем отрезке [x0, x0+d] = [0,1] выполнилось равенство 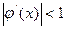 . Разрешим уравнение относительно х следующим образом:
. Разрешим уравнение относительно х следующим образом: 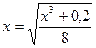 , положим
, положим 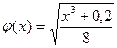 .
.
Проверим условие
сходимости: 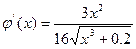
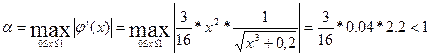 ,
,
так как х0=0,2 и d=1, то справедливость
неравенств  очевидна:
очевидна: 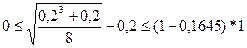
За начальное приближение возьмем х0=0,25. Все
остальные приближения будем определять из итерационной формулы 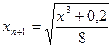
Результаты вычисления
представлены в таблице
|
n
|
xn
|
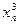
|
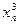 +0,2 +0,2
|
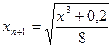
|
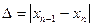
|
|
0
|
0,25
|
0,015625
|
0,215625
|
0,164174069
|
0,085825931
|
|
1
|
0,164174
|
0,004425004
|
0,204425
|
0,15985345
|
0,004320619
|
|
2
|
0,159853
|
0,004084755
|
0,204085
|
0,159720363
|
0,000133087
|
|
3
|
0,15972
|
0,004074561
|
0,204075
|
0,159716374
|
3,989E-06
|
|
4
|
0,159716
|
0,004074256
|
0,204074
|
0,159716255
|
1,19461E-07
|
|
5
|
0,159716
|
0,004074247
|
0,204074
|
0,159716251
|
3,57748E-09
|
Ответ: искомое значение корня уравнения в интервале, полученного методом простой
итерации, после исполнения четырех итераций хn = 0,159716.
Результаты нахождения корня уравнения 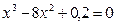 в интервале [0,2; 1,2] методом Ньютона сведены в таблице:
в интервале [0,2; 1,2] методом Ньютона сведены в таблице:
|
k
|
Xk-1
|
f(xk-1)
|
f’(xk-1)
|
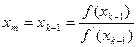
|
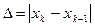
|
|
0
|
0,25
|
0,015625
|
0,215625
|
0,164174069
|
0,085825931
|
|
1
|
0,164174
|
0,004425004
|
0,204425
|
0,15985345
|
0,004320619
|
|
2
|
0,159853
|
0,004084755
|
0,204085
|
0,159720363
|
0,000133087
|
|
3
|
0,15972
|
0,004074561
|
0,204075
|
0,159716374
|
3,989E-06
|
Ответ: искомое значение корня уравнения 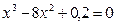 в интервале[0,2; 1,2], полученного методом Ньютона после
исполнения четырех итераций хn = 0,159853.
в интервале[0,2; 1,2], полученного методом Ньютона после
исполнения четырех итераций хn = 0,159853.
Задача 2
Методом Гаусса – Зейделя решить с точностью Е = 0,001
систему линейных уравнений:
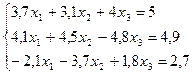
Решение:
1. Приведем систему с диагональным преобладанием. Прибавив к первому уравнению
системы удвоенное второе уравнение, получим систему эквивалентную исходной:
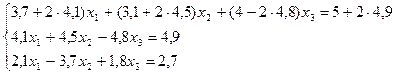
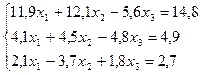
Проверим достаточное условие сходимости:
11,9 > 12,1 - 5,6= 6,5
4,5 > 4,1 - 4,8= -0,7
1,8 > 2,1 - 3,7= -1,6
Вывод итерационных формул. Для получения итерационных формул
каждое уравнение системы разрешаем относительно диагонального неизвестного,
получим эквивалентную систему:
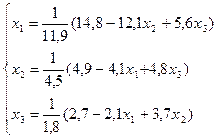
Следовательно система рекуррентных соотношений для решения
методом Гаусса-Зейделя рассматриваемой системы имеет вид:
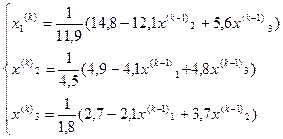
Нахождение приближенного решения. За начальное (нулевое)
приближение можно взять любой набор чисел, и, несмотря на это, диагональное
преобладание обеспечит сходимость к
точному решению. Положим 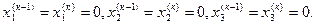
Вычислим:
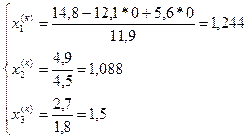
Продолжаем вычисления:
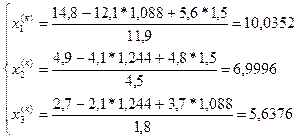
Аналогично провели четыре итерации.
Ответ: приближенным решением системы является вектор
(10,0352; 6,9996; 5,6376).