Министерство образования РФ
Всероссийский заочный финасово-экономический институт
Контрольная
работа
по дисциплине
«Эконометрика»
Вариант№9
Факультет: Финансы и кредит
Группа: 31
№ зач.книжки: 04ФФБ01009
Студент: А.В. Никишова
Преподаватель: О.М. Гусарова
Смоленск 2007
Задание.
По предприятиям легкой промышленности региона получена
информация, характеризующая зависимость объема выпуска продукции (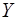
, млн. руб.) от объема капиталовложений (
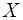, млн. руб.)
Требуется:
Найти параметры уравнения линейной регрессии, дать
экономическую интерпретацию коэффициента регрессии.
Вычислить остатки; найти остаточную сумму квадратов;
оценить дисперсию остатков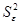 
; построить график остатков.
Проверить выполнение предпосылок МНК.
Осуществить проверку значимости параметров уравнения
регрессии с помощью t-критерия Стьюдента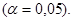 
Вычислить коэффициент детерминации, проверить
значимость уравнения регрессии с помощью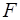 
- критерия Фишера 
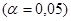, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
Осуществить прогнозирование среднего значения
показателя 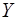при уровне значимости 
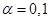, если прогнозное значения фактора Х составит
80% от его максимального значения.
Представить графически: фактические и модельные
значения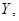 
точки прогноза.
Составить уравнения нелинейной регрессии:
·
гиперболической;
·
степенной;
·
показательной.
Привести графики построенных уравнений регрессии.
Для указанных моделей найти коэффициенты детерминации,
коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим
характеристикам и сделать вывод.
|
X
|
12
|
4
|
18
|
27
|
26
|
29
|
1
|
13
|
26
|
5
|
|
Y
|
21
|
10
|
26
|
33
|
34
|
37
|
9
|
21
|
32
|
14
|
Решение.
1. Найти параметры уравнения линейной регрессии, дать
экономическую интерпретацию коэффициента регрессии.
Расчет параметров линейного уравнения множественной регрессии с полным
перечнем факторов проводиться с помощью инструмента анализа данных Регрессия:
1) в главном меню выберем
последовательно пункты СервисðАнализ данныхðРегрессия;
2) в диалоговом окне Регрессия в поле Входной интервал Y вводим адрес одного диапазона ячеек,
который представляет зависимую переменную. В поле Входной интервал Х вводим
адрес диапазона, который содержит значения независимых переменных
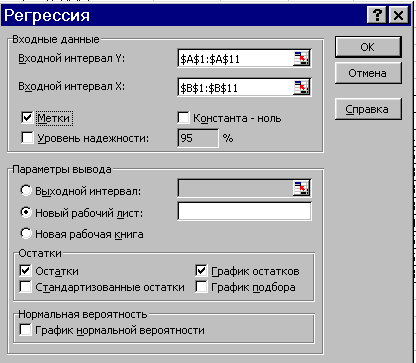
5) устанавливаем необходимые флажки и нажимаем ОК.
Результат
регрессионного анализа:
Таблица 1
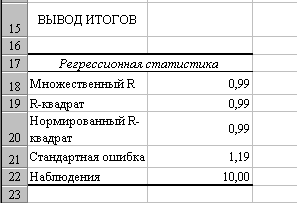
Таблица 2
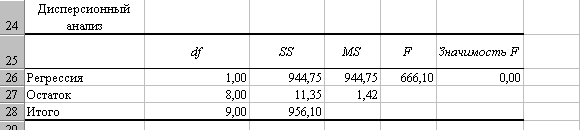
Таблица 3
Уравнение регрессии зависимости объема выпуска
продукции от объема капиталовложений можно записать в следующем виде:
у = 8,12 +
0,97х
С увеличением объема капиталовложений на 1 млн руб.
объем выпускаемой продукции увеличиться в среднем на 970 тыс. руб. Это
свидетельствует об эффективности работы предприятий.
2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию
остатков 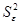; построить график остатков.
Вычисление остатков
производим с помощью СервисðАнализ данныхðРегрессия
(п.1)
Таблица 4
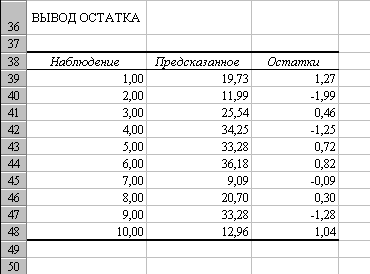
Остаточная
сумма квадратов:
∑e(t)2
Это
значение можно найти в третьем столбце
таблицы 2, равное – 11,35.
Дисперсия
остатков S2 = 1,42
(значение из 4 столбца таблицы 2).
3.
Проверить выполнение предпосылок
МНК.
Предпосылки МНК:
1) В задании у (объем выпуска продукции) является
результативным признаком, а х1 (объем капиталовложений) – факторным
признаком.
2) Так как у нас парная регрессия, то
отсутствие мультиоколлинеарности выполняется автоматически.
3)
Наличие (отсутствие) автокорреляции в отклонениях проверяют с помощью
критерия Дарбина-Уотсона. Численное значение коэффициента равно:
|
dw=
|
S(ei-ei-1)
|
,
где eI=yi-y
|
|
Se2i
|
|
t
|
y
|
y
|
εi= y - y
|
εi2
|
εi-1
|
εi - εi-1
|
(εi - εi-1)2
|
|
1
|
21,0000
|
21,4454
|
-0,4454
|
0,1984
|
|
|
|
|
2
|
10,0000
|
10,8655
|
-0,8655
|
0,7491
|
-0,4454
|
-0,4201
|
0,1765
|
|
3
|
26,0000
|
24,1743
|
1,8257
|
3,3332
|
-0,8655
|
2,6912
|
7,2426
|
|
4
|
33,0000
|
33,0756
|
-0,0756
|
0,0057
|
1,8257
|
-1,9013
|
3,6148
|
|
5
|
34,0000
|
33,7793
|
0,2207
|
0,0487
|
-0,0756
|
0,2962
|
0,0878
|
|
6
|
37,0000
|
39,5442
|
-2,5442
|
6,4729
|
0,2207
|
-2,7649
|
7,6445
|
|
7
|
9,0000
|
10,3592
|
-1,3592
|
1,8476
|
-2,5442
|
1,1849
|
1,4041
|
|
8
|
21,0000
|
19,2730
|
1,7270
|
2,9824
|
-1,3592
|
3,0862
|
9,5246
|
|
9
|
32,0000
|
35,0505
|
-3,0505
|
9,3053
|
1,7270
|
-4,7774
|
22,8237
|
|
10
|
14,0000
|
9,4329
|
4,5671
|
20,8584
|
-3,0505
|
7,6176
|
58,0273
|
|
|
|
|
|
45,8017
|
-4,5671
|
5,0125
|
110,5458
|
dw
= 110,5458 / 45,8017 = 2,4135
Определим выполняется МНК или нет:
1,08 1,36 2
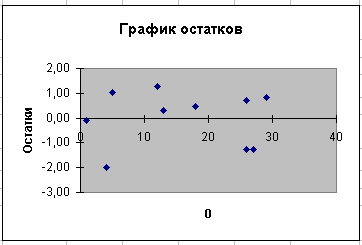
На оси
найдем точку dw = 2,4135, она находится в IV области. Следовательно, можно
сделать вывод о том, что автокорреляция остатков в ряду динамики присутствует.
4) Равенство математического ожидания
остатков 0 проверяется по t-критерию Стьюдента.
Проанализировав сумму остатков
(таблица 4) получили -1,33 * 10-14 / 10 ≈ 0. значит t = (׀ Ē ׀/ SE) * √
n → 0, следовательно, данная предпосылка МНК
выполняется, так как tтабл = 2,31 > t
5) Постоянная дисперсия (т.е.
выполнение свойства гомоскедастичности по тесту Голдфельда-Квандта)
· Упорядочим n наблюдений по мере возрастания
переменой х.
· Разделим исходный блок на 3 части,
причем 1 3 части равны по размеру n = 4
· 2 часть из рассмотрения исключается.
· Для 1 и 3 частей строится уравнения
регрессии.
1 уравнение
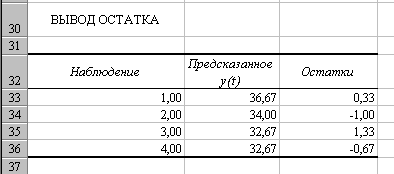
2 уравнение
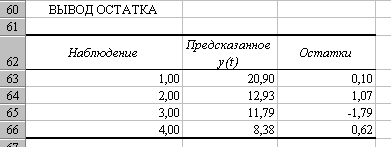
Следовательно уравнения регрессии
будут иметь вид:
у1 = 0,048 + 0,796х1
у2 = -2 + 1,33х1
По
уравнениям регрессии определяется остаточная дисперсия. Сравнение дисперсий
происходит по F-критерию Фишера.
Если Fнаблюд. =S1ŷ/S2ŷ >Fкр.(a;k1;k2), то выполняется свойство гомоскедастичности (ГО)
Если F расч > F табл, то имеет место гетероскедастичность
(ГЕ).
Чтобы найти значение F табл данного критерия определим степени свободы по
формуле
К1=К2=(n-C-2*p)/2
n=10,
C=2 – количество исключаемых
наблюдений во 2 части блока исходных данных
р=1 – число факторов
К1=К2=(10-2-2*1)/2 = 3
F табл = 10,13
Найдем F расч
σ2 = ∑ εi2 / (n-1)
σ2(1 ур.) = 3,33 / 9
= 0,37
σ2(2 ур.) = 4,75 / 9
= 0,53
F расч = 0,53 / 0,37 = 1,4324
Так
как F расч < F табл , то можно сказать что больше нарушена предпосылка о
равенстве дисперсий остаточных величин и следовательно выполняется свойство
гомоскедастичности.
4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента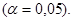
Статистическую значимость параметров уравнения
регрессии оценим с помощью t-критерия Стъюдента.
taj = aj / Sa j= aj / Se×√bjj
Расчетные значения t-критерия Стъюдента для коэффициентов
уравнения регрессии а приведены в четвертом столбце таблицы 3
протокола Excel и составляет – 25,81. Табличное значение t-критерия Стъюдента можно найти с помощью функции
СТЬЮДРАСПОБР
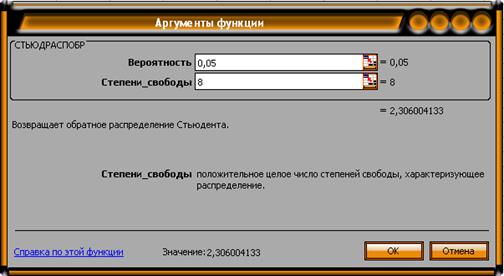
Табличное значение t-критерия при 5% уровне значимости и
степенях свободы (10-1-1) составляет 2,31. Так как ׀tа׀>tтабл, то коэффициент а1 признается
статистически значимым.
5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии
с помощью 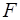- критерия Фишера 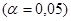, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
Проверку значимости уравнения регрессии произведем
на основе вычисления F-критерия Фишера.
R2
(n-k-1)
F =
(1-R2)/ k
Значение F-критерия Фишера можно найти в таблице
2 протокола Excel, равное 666,10.
Табличное значение F-критерия можно найти с помощью
функции FРАСПОБР.
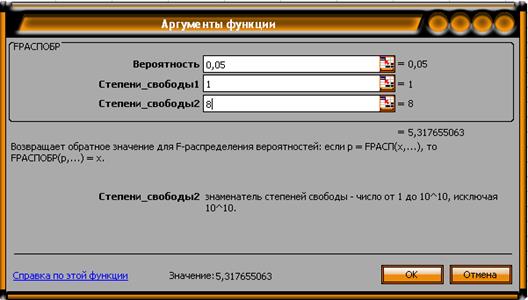
Поскольку
Fрас > Fтабл,
уравнение регрессии следует признать адекватным.
Оценим качество уравнения регрессии с помощью
коэффициента детерминации.
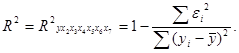
Значение коэффициента детерминации
можно найти в таблице 1 - R2 = 0,99.
99% вариации объема выпуска продукции учтено в
модели и обусловлено влиянием объема капиталовложений.
Найдем среднюю относительную ошибку
аппроксимакции:
Ēотн = (1/ n) * ∑(Ei/y) * 100%
Ēотн = 0,1 * 49,7% = 4,97%
В среднем расчетные значения у для линейной модели отличаются
от фактических на 4,97%.
6. Осуществить прогнозирование
среднего значения показателя 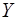при уровне
значимости 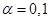, если прогнозное значения фактора Х составит
80% от его максимального значения.
хпр = 0,8 × хmax
упр = a + b * xпр
хпр
= 0,8 * 29 = 23,2
упр
= 8,12 + 0,97*23,2 = 30,624
7. Представить графически: фактические и модельные
значения 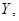точки прогноза.
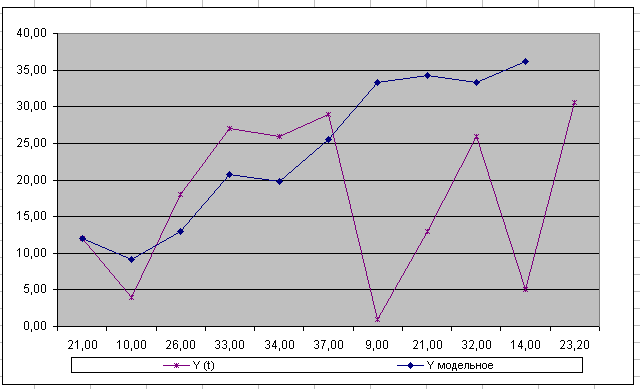
8. Составить уравнения нелинейной регрессии:
·
гиперболической;
Уравнение
гиперболической функции: ŷ = a + b / x.
Произведем
линеаризацию модели путем замены Х = 1/х. В результате получим линейное
уравнение: ŷ = a + b *X.
Рассчитаем
его параметры по данным таблицы 4.
Таблица 4
|
t
|
y
|
x
|
Х
|
yX
|
X2
|
Y-Yср
|
Y-Yср)2
|
y
|
|
1
|
21,00
|
12,00
|
0,08
|
1,75
|
0,01
|
-2,70
|
7,29
|
26,03
|
|
2
|
10,00
|
4,00
|
0,25
|
2,50
|
0,06
|
-28,40
|
806,56
|
22,07
|
|
3
|
26,00
|
18,00
|
0,06
|
1,44
|
0,00
|
-12,40
|
153,76
|
26,69
|
|
4
|
33,00
|
27,00
|
0,04
|
1,22
|
0,00
|
-5,40
|
29,16
|
27,12
|
|
5
|
34,00
|
26,00
|
0,04
|
1,31
|
0,00
|
-4,40
|
19,36
|
27,09
|
|
6
|
37,00
|
29,00
|
0,03
|
1,28
|
0,00
|
-1,40
|
1,96
|
27,19
|
|
7
|
9,00
|
1,00
|
1,00
|
9,00
|
1,00
|
-29,40
|
864,36
|
4,29
|
|
8
|
21,00
|
13,00
|
0,08
|
1,62
|
0,01
|
-17,40
|
302,76
|
26,18
|
|
9
|
32,00
|
26,00
|
0,04
|
1,23
|
0,00
|
-6,40
|
40,96
|
27,09
|
|
10
|
14,00
|
5,00
|
0,20
|
2,80
|
0,04
|
-24,40
|
595,36
|
23,26
|
|
Итого
|
237,00
|
161,00
|
1,81
|
24,15
|
1,12
|
-132,30
|
2
821,53
|
237,00
|
|
Ср.знач.
|
23,70
|
16,10
|
0,18
|
2,41
|
0,11
|
-13,23
|
282,15
|
23,70
|
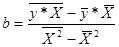=-23,72.
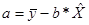=28,00.
Получим следующее уравнение
гиперболической модели:
y =
28,003-23,72/x
·
cтепенной;
Уравнение
степенной модели имеет вид: ŷ=a*xb.
Для
построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих
частей уравнения:
lg ŷ=lg a + b lg x.
Таблица 5
|
|
у(t)
|
x
|
lgY
|
lgX
|
|
1
|
21,00
|
12,00
|
1,32
|
1,08
|
|
2
|
10,00
|
4,00
|
1,00
|
0,60
|
|
3
|
26,00
|
18,00
|
1,41
|
1,26
|
|
4
|
33,00
|
27,00
|
1,52
|
1,43
|
|
5
|
34,00
|
26,00
|
1,53
|
1,41
|
|
6
|
37,00
|
29,00
|
1,57
|
1,46
|
|
7
|
9,00
|
1,00
|
0,95
|
0,00
|
|
8
|
21,00
|
13,00
|
1,32
|
1,11
|
|
9
|
32,00
|
26,00
|
1,51
|
1,41
|
|
10
|
14,00
|
5,00
|
1,15
|
0,70
|
|
Итого
|
237,00
|
161,00
|
13,28
|
10,47
|
|
среднее
|
23,70
|
16,10
|
1,33
|
1,05
|
Обозначим Y = lg
ŷ, X = lg x, A = lg a. Тогда
уравнение примет вид Y=A+b*X – линейное уравнение
регрессии.
Рассчитаем параметры,
используя данные таблицы 6.
Таблица 6
|
|
у(t)
|
x
|
lgY
|
lgX
|
YX
|
X2
|
x*b
|
ŷ
|
ei
|
ei2
|
|ei/yi|*100%
|
|
1
|
21,00
|
12,00
|
1,32
|
1,08
|
1,43
|
1,16
|
3,08
|
2,63
|
-1,31
|
1,72
|
99,06
|
|
2
|
10,00
|
4,00
|
1,00
|
0,60
|
0,60
|
0,36
|
1,87
|
1,60
|
-0,60
|
0,36
|
60,01
|
|
3
|
26,00
|
18,00
|
1,41
|
1,26
|
1,78
|
1,58
|
3,70
|
3,16
|
-1,75
|
3,06
|
123,53
|
|
4
|
33,00
|
27,00
|
1,52
|
1,43
|
2,17
|
2,05
|
4,45
|
3,80
|
-2,28
|
5,21
|
150,29
|
|
5
|
34,00
|
26,00
|
1,53
|
1,41
|
2,17
|
2,00
|
4,38
|
3,74
|
-2,20
|
4,86
|
143,96
|
|
6
|
37,00
|
29,00
|
1,57
|
1,46
|
2,29
|
2,14
|
4,60
|
3,93
|
-2,36
|
5,56
|
150,33
|
|
7
|
9,00
|
1,00
|
0,95
|
0,00
|
0,00
|
0,00
|
1,00
|
0,85
|
0,10
|
0,01
|
10,52
|
|
8
|
21,00
|
13,00
|
1,32
|
1,11
|
1,47
|
1,24
|
3,20
|
2,73
|
-1,41
|
1,98
|
106,42
|
|
9
|
32,00
|
26,00
|
1,51
|
1,41
|
2,13
|
2,00
|
4,38
|
3,74
|
-2,23
|
4,98
|
148,23
|
|
10
|
14,00
|
5,00
|
1,15
|
0,70
|
0,80
|
0,49
|
2,07
|
1,77
|
-0,62
|
0,39
|
54,46
|
|
Итого
|
237,00
|
161,00
|
13,28
|
10,47
|
14,84
|
13,02
|
32,73
|
27,95
|
-14,66
|
28,11
|
1 046,80
|
|
среднее
|
23,70
|
16,10
|
1,33
|
1,05
|
1,48
|
1,30
|
|
2,79
|
-1,47
|
2,81
|
104,68
|
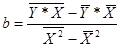=0,45.
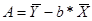=0,85.
Уравнение регрессии будет иметь вид ŷ = 0,85 - 0,45x.
Перейдем к исходным переменным х и у, выполнив
потенцирование данного уравнения:
ŷ = 100,85*х0,84.
Получим уравнение
ŷ=7,14*х0,45.
·
показательной.
Уравнение показательной
кривой: ŷ = a*bx.
Для построения этой
модели необходимо произвести линеаризацию переменных. Для этого осуществим
логарифмирование обеих частей уравнения:
lg ŷ = lg a + lg x*b.
Обозначим Y
= lg ŷ, B = lg b, A = lg a.
Получим линейное
уравнение регрессии:
Y = A + B*x.
|
t
|
y
|
x
|
Y
|
Yx
|
x2
|
Y-Yср
|
Y-Yср)2
|
x-xs
|
x-xs)2
|
y
|
Е
|
у-у)2
|
E/у*100
|
|
1
|
21,00
|
12,00
|
1,32
|
15,87
|
144,00
|
-0,01
|
0,00
|
-4,10
|
16,81
|
17,5331
|
3,4669
|
12,02
|
16,51
|
|
2
|
10,00
|
4,00
|
1,00
|
4,00
|
16,00
|
-0,57
|
0,33
|
-12,10
|
146,41
|
11,9970
|
-1,9970
|
3,99
|
19,97
|
|
3
|
26,00
|
18,00
|
1,41
|
25,47
|
324,00
|
-0,16
|
0,02
|
1,90
|
3,61
|
23,3050
|
2,6950
|
7,26
|
10,37
|
|
4
|
33,00
|
27,00
|
1,52
|
41,00
|
729,00
|
-0,05
|
0,00
|
10,90
|
118,81
|
35,7136
|
-2,7136
|
7,36
|
8,22
|
|
5
|
34,00
|
26,00
|
1,53
|
39,82
|
676,00
|
-0,04
|
0,00
|
9,90
|
98,01
|
34,0593
|
-0,0593
|
0,00
|
0,17
|
|
6
|
37,00
|
29,00
|
1,57
|
45,48
|
841,00
|
0,00
|
0,00
|
12,90
|
166,41
|
39,2673
|
-2,2673
|
5,14
|
6,13
|
|
7
|
9,00
|
1,00
|
0,95
|
0,95
|
1,00
|
-0,62
|
0,38
|
-15,10
|
228,01
|
10,4059
|
-1,4059
|
1,98
|
15,62
|
|
8
|
21,00
|
13,00
|
1,32
|
17,19
|
169,00
|
-0,25
|
0,06
|
-3,10
|
9,61
|
18,3848
|
2,6152
|
6,84
|
12,45
|
|
9
|
32,00
|
26,00
|
1,51
|
39,13
|
676,00
|
-0,07
|
0,00
|
9,90
|
98,01
|
34,0593
|
-2,0593
|
4,24
|
6,44
|
|
10
|
14,00
|
5,00
|
1,15
|
5,73
|
25,00
|
-0,43
|
0,18
|
-11,10
|
123,21
|
12,5797
|
1,4203
|
2,02
|
10,14
|
|
Итого
|
237,0
|
161,0
|
13,28
|
234,64
|
3 601,00
|
-2,20
|
0,99
|
0,00
|
1 008,90
|
237,31
|
-0,31
|
50,85
|
106,02
|
|
Ср.знач.
|
23,7
|
16,1
|
1,33
|
23,46
|
360,10
|
-0,22
|
0,10
|
0,00
|
100,89
|
23,73
|
-0,03
|
5,09
|
10,60
|
Рассчитаем его параметры,
используя данные таблицы 7.
Таблица 7
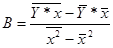=0,0206
=1,00
Уравнение будет иметь
вид:
Y= 1,00-0,0206*х.
Перейдем к исходным переменным
х и у. выполнив потенцирование данного уравнения:
ŷ = 101,00*(100,0206)х
=1,05*9,924х.
Привести графики построенных уравнений регрессии.
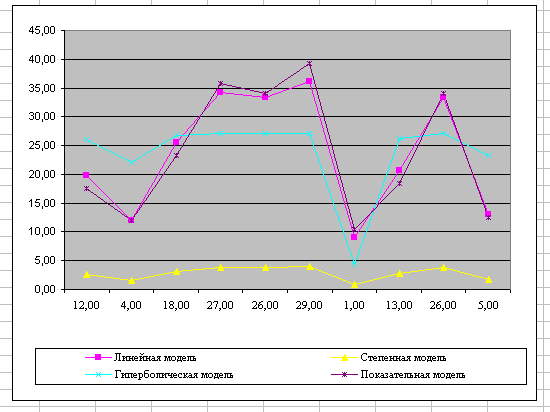
Графики построенных уравнений регрессий
9.
Для указанных моделей найти
коэффициенты детерминации,
коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим
характеристикам и сделать вывод.
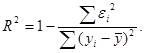
R2 гип = 0,46
R2 степ = 0,96
R2 показ = 0,98
Найдем коэффициенты эластичности:
.
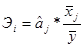Эгип = 28,00 * 16,1/23,7 = 19,0204
Эстеп = 0,85 * 16,1/23,7 = 0,5774
Эпок =
1,00* 16,1/23,7 = 0,6793
Найдем средние относительные ошибки аппроксимакции:
.
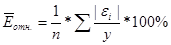Ēотн степ = 0,1 * 1046,8%
= 104,68%
Ēотн гип = 0,1 * 237,00% = 23,70%
Ēотн показ = 0,1 * 106,02% = 10,602%
Для
выбора лучшей модели построим сводную таблицу результатов.
Таблица 8
|
Модель
|
Уравнение регрессии
|
R2
|
F-критерий
Фишера
|
Eотн.
|
|
Линейная
|
у
= 8,12 + 0,97х
|
0,99
|
666,10
|
4,967
|
|
Степенная
|
ŷ=7,14*х0,45
|
0,96
|
210,77
|
104,68
|
|
Показательная
|
ŷ = 1,05*9,924х
|
0,98
|
339,59
|
10,602
|
|
Гиперболическая
|
ŷ = 28,003-23,72/x.
|
0,46
|
6,82
|
23,70
|
Сравнив модели по данным
характеристикам можно сделать вывод, самое большее значение F-критерия Фишера и большое значение
коэффициента детерминации R2 имеет линейная модель, но т.к. у нее самая маленькая Eотн., то лучшей для построения прогнозов
является показательная модель.