Всероссийский заочный финансово-экономический институт
Контрольная
работа
по дисциплине «Статистика»
Вариант № 1
Выполнил:
Проверил:
Тула, 2006 г.
Задача № 1.
Имеются следующие
данные о распределении населения по размерам среднедушевого денежного дохода
региона за месяц:
|
Доход, руб.
|
Население, тыс. чел.
|
|
до 200
|
14
|
|
200-400
|
162
|
|
400-600
|
264
|
|
600-800
|
302
|
|
800-1200
|
396
|
|
1200-1600
|
198
|
|
1600-2000
|
86
|
|
2000-2400
|
40
|
|
2400-2800
|
20
|
|
2800-3200
|
6
|
|
свыше 3200
|
10
|
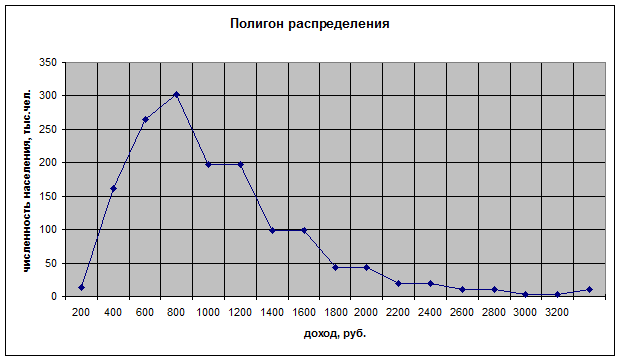
Постройте новый ряд
распределения с равными интервалами (200 руб.), используя метод вторичной
группировки. Определите среднедушевой денежный доход, среднее квадратичное
отклонение, коэффициент вариации, моду и медиану. Постройте графики.
Определите, какая из средних наиболее правильно характеризует среднедушевой
доход населения.
Решение:
1. Для построения
нового ряда распределения с интервалами равными 200 руб. с использованием
метода вторичной группировки проведем следующие действия: в интервале 800 –
1200 равном 400 руб. разделим численность населения пополам и определим границы
двух новых равных интервалов (200 руб.). В результате получим два интервала:
800 – 1000 и 1000 – 1200 с численностью населения в каждом 396/2=198.
Аналогично посчитаем численность населения в следующих интервалах равных 400
руб. и построим новый ряд распределения. Результаты сведем в таблицу:
|
Доход, руб.
|
Население, тыс. чел.
|
|
До 200
|
14
|
|
200-400
|
162
|
|
400-600
|
264
|
|
600-800
|
302
|
|
800-1000
|
198
|
|
1000-1200
|
198
|
|
1200-1400
|
99
|
|
1400-1600
|
99
|
|
1600-1800
|
43
|
|
1800-2000
|
43
|
|
2000-2200
|
20
|
|
2200-2400
|
20
|
|
2400-2600
|
10
|
|
2600-2800
|
10
|
|
2800-3000
|
3
|
|
3000-3200
|
3
|
|
свыше 3200
|
10
|
|
Итого
|
1498
|
2.
Среднедушевой денежный доход определим по формуле:
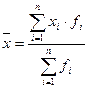 ,
,
где 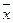 - средняя
арифметическая взвешенная;
- средняя
арифметическая взвешенная;
fi – веса (частота повторения одинаковых признаков);
∑ хi∙fi – сумма произведений величины признаков на их частоты;
∑ fi – общая
численность единиц совокупности.
В данном случае значения осредняемого
признака (дохода) заданы в виде интервальных рядов распределения с открытыми
интервалами. Поэтому при расчете в качестве значений признаков в группах
принимаем середины этих интервалов, при этом величины открытых интервалов
условно приравниваются к интервалам, примыкающим к ним (второй и
предпоследний). Вычисления сведем в таблицу:
|
Доход, руб.
|
Население,
тыс. чел.
f
|
Середина интервала, руб.
х
|
х∙f
|
|
до 200
|
14
|
100
|
1400
|
|
200-400
|
162
|
300
|
48600
|
|
400-600
|
264
|
500
|
132000
|
|
600-800
|
302
|
700
|
211400
|
|
800-1000
|
198
|
900
|
178200
|
|
1000-1200
|
198
|
1100
|
217800
|
|
1200-1400
|
99
|
1300
|
128700
|
|
1400-1600
|
99
|
1500
|
148500
|
|
1600-1800
|
43
|
1700
|
73100
|
|
1800-2000
|
43
|
1900
|
81700
|
|
2000-2200
|
20
|
2100
|
42000
|
|
2200-2400
|
20
|
2300
|
46000
|
|
2400-2600
|
10
|
2500
|
25000
|
|
2600-2800
|
10
|
2700
|
27000
|
|
2800-3000
|
3
|
2900
|
8700
|
|
3000-3200
|
3
|
3100
|
9300
|
|
свыше 3200
|
10
|
3300
|
33000
|
|
Итого
|
1498
|
-
|
1412400
|
Тогда средний доход на душу
населения будет равен:
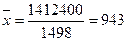 руб.
руб.
3. Вычислим среднее кавадратическое отклонение по
формуле:
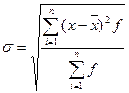
Результаты
вычислений сведем в таблицу:
|
Середина интервала, руб.
х
|
Население,
тыс. чел.
f
|
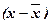
|
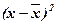
|
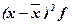
|
|
100
|
14
|
-843
|
710649
|
9949086
|
|
300
|
162
|
-643
|
413449
|
66978738
|
|
500
|
264
|
-443
|
196249
|
51809736
|
|
700
|
302
|
-243
|
59049
|
17832798
|
|
900
|
198
|
-43
|
1849
|
366102
|
|
1100
|
198
|
157
|
24649
|
4880502
|
|
1300
|
99
|
357
|
127449
|
12617451
|
|
1500
|
99
|
557
|
310249
|
30714651
|
|
1700
|
43
|
757
|
573049
|
24641107
|
|
1900
|
43
|
957
|
915849
|
39381507
|
|
2100
|
20
|
1157
|
1338649
|
26772980
|
|
2300
|
20
|
1357
|
1841449
|
36828980
|
|
2500
|
10
|
1557
|
2424249
|
24242490
|
|
2700
|
10
|
1757
|
3087049
|
30870490
|
|
2900
|
3
|
1957
|
3829849
|
11489547
|
|
3100
|
3
|
2157
|
4652649
|
13957947
|
|
3300
|
10
|
2357
|
5555449
|
55554490
|
|
Итого
|
1498
|
-
|
26061833
|
458888602
|
Тогда среднее квадратическое
отклонение будет равно:
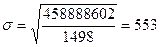 руб.
руб.
4. Определим
коэффициент вариации:
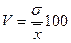 =
=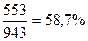
Данный коэффициент показывает степень
вариации признаков. Чем больше его величина, тем больше разброс значений вокруг
средней, тем менее однородна совокупность по составу. В данном случае наблюдается
достаточно большой разброс доходов населения относительно среднего значения.
5. Мода – это значение
признака, наиболее часто встречающееся в совокупности. Для интервальных вариационных
рядов распределения мода рассчитывается по формуле:
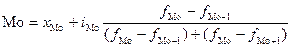 ,
,
где Мо – мода;
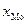 - нижняя граница
модального интервала;
- нижняя граница
модального интервала;
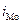 - величина модального
интервала;
- величина модального
интервала;
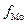 - частота модального
интервала;
- частота модального
интервала;
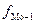 - частота интервала,
предшествующая модальному;
- частота интервала,
предшествующая модальному;
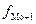 - частота интервала,
следующего за модальным.
- частота интервала,
следующего за модальным.
Первоначально по наибольшей частоте
признака (дохода) определим модальный интервал. Наибольшее число населения –
302 человека – имеют заработную плату в интервале 600 – 800 руб., который и
является модальным.
В результате расчетов получим:
Мо =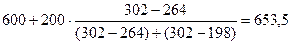 руб.
руб.
6. Медианой называется
вариант, расположенный в середине упорядоченного вариационного ряда, делящий
его на две равные части.
Для интервальных вариационных рядов
медиана рассчитывается по формуле:
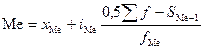 ,
,
где Ме – медиана;
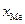 - нижняя граница медианного интервала;
- нижняя граница медианного интервала;
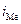 - величина медианного интервала;
- величина медианного интервала;
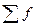 - сумма частот ряда;
- сумма частот ряда;
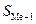 - сумма накопленных
частот ряда, предшествующих медианному интервалу;
- сумма накопленных
частот ряда, предшествующих медианному интервалу;
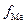 - частота медианного
интервала.
- частота медианного
интервала.
Определяем медианный
интервал, в котором находится порядковый номер медианы. Для этого подсчитываем
сумму частот накопленным итогом того числа, превышающего половину объема
совокупности (1498/2=749). Сведем расчет в таблицу:
|
Доход, руб.
|
Население,
тыс. чел.
|
Сумма накопленных частот
|
|
до 200
|
14
|
14
|
|
200-400
|
162
|
176
|
|
400-600
|
264
|
440
|
|
600-800
|
302
|
742
|
|
800-1000
|
198
|
940
|
|
1000-1200
|
198
|
-
|
|
1200-1400
|
99
|
-
|
|
1400-1600
|
99
|
-
|
|
1600-1800
|
43
|
-
|
|
1800-2000
|
43
|
-
|
|
2000-2200
|
20
|
-
|
|
2200-2400
|
20
|
-
|
|
2400-2600
|
10
|
-
|
|
2600-2800
|
10
|
-
|
|
2800-3000
|
3
|
-
|
|
3000-3200
|
3
|
-
|
|
свыше 3200
|
10
|
-
|
|
Итого
|
1498
|
-
|
В данном случае значение 940 соответствует
интервалу 800 – 1000. Это и есть медианный интервал, в котором находится
медиана. В результате чего получим:
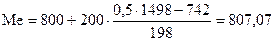 руб.
руб.
Задача №
2.
Для определения среднего размера вклада в
банке было проведено выборочное обследование 10 000 счетов (выборка
10%-ная, механическая). В результате выборки установлено, что средний размер
вклада составил 2000 руб. при среднем квадратическом отклонении 800 руб.
С вероятностью 0,954 определите границы, в
которых будет находиться средний размер вклада в банке.
Решение:
Средний
размер вклада будет находиться в пределах:
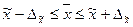
где 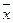 - средний размер вклада;
- средний размер вклада;
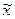 - выборочная средняя;
- выборочная средняя;
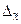 - ошибка выборки.
- ошибка выборки.
Так как
выборка механическая, то ошибка выборки определяется по следующей формуле:
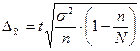 ,
,
где σ2
– дисперсия (квадрат среднего квадратического отклонения);
n – численность
выборки, n = 10 000;
N –
численность генеральной совокупности;
t – коэффициент
доверия, определяющийся по таблице значений интегральной функции Лапласа. При
вероятности 0,954 имеем t = 2.
В результате
получим:
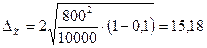
Тогда границы,
в которых находится средний размер вклада определим следующим образом:
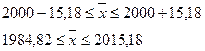
Задача №
3.
По следующим данным о
кредитных вложениях в экономику (млн. руб.) определите: средний размер
кредитных вложений по всей совокупности и по видам кредитов, показатели
вариации и структуры. Сделайте выводы.
|
Показатель
|
1.01
|
1.02
|
1.03
|
1.04
|
1.05
|
1.06
|
|
Кредитные вложения
Всего
|
30,0
|
33,1
|
35,4
|
38,9
|
43,7
|
48,0
|
|
В том числе:
краткосрочные
|
29,0
|
32,0
|
34,2
|
37,5
|
41,9
|
45,7
|
|
долгосрочные
|
1,0
|
1,1
|
1,2
|
1,4
|
1,8
|
2,3
|
Решение:
1. По условию
задачи имеем моментный ряд динамики с равными интервалами, поэтому средний
уровень ряда будет исчислен по формуле средней хронологической:
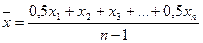 ;
;
где n – число
значений, n = 6.
Рассчитаем размер
кредитных вложений:
а) по всей совокупности:
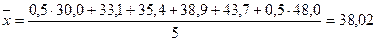
б) по краткосрочным вложениям:
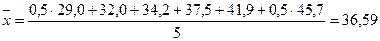
б) по долгосрочным вложениям:
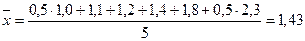
2.
Определим значения показателей вариации.
Показатели вариации
используются для измерения степени колеблемости отдельных значений признака от
средней. К ним относятся дисперсия, среднеквадратическое отклонение и
коэффициент вариации.
Для расчёта этих показателей составим
вспомогательную таблицу:
|
Показатель
|
Кредитные вложения
|
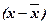
|
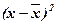
|
|
|
по всей совокупности
|
|
|
|
1.01
|
30,0
|
-8,02
|
64,32
|
|
1.02
|
33,1
|
-4,92
|
24,21
|
|
1.03
|
35,4
|
-2,62
|
6,86
|
|
1.04
|
38,9
|
0,88
|
0,77
|
|
1.05
|
43,7
|
5,68
|
32,26
|
|
1.06
|
48,0
|
9,98
|
99,60
|
|
Итого
|
х
|
х
|
228,03
|
|
|
по краткосрочным
|
|
|
|
1.01
|
29,0
|
-7,59
|
57,61
|
|
1.02
|
32,0
|
-4,59
|
21,07
|
|
1.03
|
34,2
|
-2,39
|
5,71
|
|
1.04
|
37,5
|
0,91
|
0,83
|
|
1.05
|
41,9
|
5,31
|
28,20
|
|
1.06
|
45,7
|
9,11
|
82,99
|
|
Итого
|
х
|
х
|
196,40
|
|
|
по долгосрочным
|
|
|
|
1.01
|
1,0
|
-0,43
|
0,18
|
|
1.02
|
1,1
|
-0,33
|
0,11
|
|
1.03
|
1,2
|
-0,23
|
0,05
|
|
1.04
|
1,4
|
-0,03
|
0,00
|
|
1.05
|
1,8
|
0,37
|
0,14
|
|
1.06
|
2,3
|
0,87
|
0,76
|
|
Итого
|
х
|
х
|
1,24
|
Дисперсию, среднее квадратическое отклонение и коэффициент вариации определим
по следующим формулам:
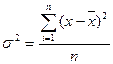 ,
,
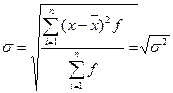 ,
,
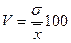
Результаты
вычислений сведем в таблицу:
|
Показатели вариации
|
Дисперсия
|
Среднее
квадратическое отклонение
|
коэффициент
вариации
|
|
Общие кредитные вложения
|
38,01
|
6,17
|
16,23%
|
|
Краткосрочные вложения
|
32,73
|
5,72
|
15,63%
|
|
Долгосрочные вложения
|
0,21
|
0,46
|
32,17%
|
Вывод: совокупность
считается количественно однородной, если коэффициент вариации не превышает 33%.
Таким образом, совокупность вложений по всем статьям является однородной.
3. Определим
показатели структуры.
Показатели структуры характеризуют
состав изучаемой совокупности, удельные веса элементов в общем итоге и
определяются по формуле:
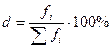 ,
,
где d – удельный вес частей совокупности
Результаты вычислений сведём в таблицу:
|
Показатель
|
Доля краткосрочных,%
|
Доля долгосрочных,%
|
|
1.01
|
96,67
|
3,33
|
|
1.02
|
96,68
|
3,32
|
|
1.03
|
96,61
|
3,39
|
|
1.04
|
96,40
|
3,60
|
|
1.05
|
95,88
|
4,12
|
|
1.06
|
95,21
|
4,79
|
Вывод:
руководствуясь данными таблицы, можно заключить, что в течении первого
полугодия наблюдается тенденция к росту долгосрочных вложений в общей доле
кредитных вложений. С января по июнь величина долгосрочных кредитов в денежном
выражении увеличилась на 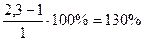
Задача № 4.
Имеются
данные по страховой организации, тыс. руб.:
|
Вид
имущества
|
Базисный
период
|
Отчетный
период
|
|
сумма выплат страхового возмещения
|
страховая сумма
|
сумма выплат страхового возмещения
|
страховая сумма
|
|
Домашнее
|
28,7
|
34 440
|
28,9
|
32 400
|
|
Строение
|
11,9
|
20 230
|
14,1
|
21 150
|
Определите: убыточность
страховых сумм по видам имущества и в целом, индексы средней убыточности
переменного состава, постоянного состава и структурных сдвигов. Сделайте
выводы.
Решение:
Убыточность страховых сумм (в процентах) определяется по формуле:
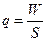 ,
,
где W – сумма
выплат страхового возмещения;
S – страховая сумма
В базисном году убыточность
составила:
а) домашнего имущества:
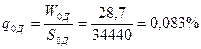 ;
;
б) строения:
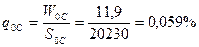 ;
;
в) имущества в целом:
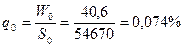 .
.
В отчётном году
получим:
а) для домашнего имущества
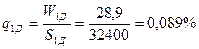
б) для строения:
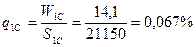
в) для имущества в целом:
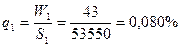 .
.
Изменение
убыточности по видам имущества в отчётном периоде:
а) для домашнего
имущества:
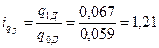
б) для строения:
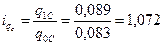
Вывод: Таким образом, даже
несмотря на снижение по домашнему имуществу страховых сумм, суммы выплат
страхового возмещения выросли; убыточность по строению выросла на 7,2%, а по
домашнему имуществу возросла на 21%.
Индекс
средней убыточности переменного состава определим по формуле:
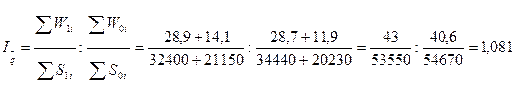
Индекс показывает, что средняя
убыточность возросла на 8,1% за счёт как изменения убыточности по имуществу,
так и размера страховых сумм.
Индекс
средней убыточности постоянного состава определим по формуле:
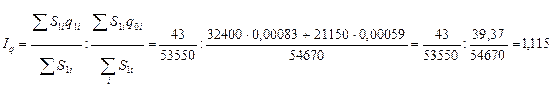
Значит, средняя убыточность
возросла на 11,5% за счёт увеличения страховых выплат.
Индекс
структурных сдвигов:
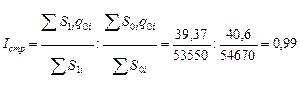
Следовательно, за счёт снижения
страховой суммы по домашнему имуществу, средняя убыточность снизилась на 1 %.
Задача №
5.
Для погашения долга 80 тыс. руб.
предприятие 21.05 выдало банку четыре одинаковых векселя со сроком погашения
21.06, 11.07, 6.08, 21.09. Определите величину каждого векселя, если известно,
что ставка составляет 36% годовых.
Решение:
Определим
величину каждого векселя. Так как по условию они одинаковы, то величина каждого
из них равна 80/4=20 тыс. руб.
Тогда величина
каждого векселя будет вычисляться по формуле:
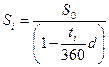 ,
,
где ti - временной
интервал от выдачи векселей до их погашения;
d=36% - учётная ставка.
t1=172-141=31дн.
– интервал времени с 21.05 по 21.06;
t2=192-141=51дн.
– интервал времени с 21.05 по 11.07;
t3=218-141=77дн.
– интервал времени с 21.05 по 06.08;
t4=264-141=123дн.
– интервал времени с 21.05 по 21.09.
В результате вычислений получим:
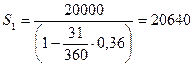 руб.
руб.
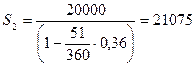 руб.
руб.
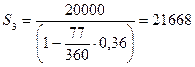 руб.
руб.