Министерство образования и науки РФ
Федеральное агентство по образованию
ГОУ ВПО
Всероссийский заочный
финансово-экономический институт
КОНТРОЛЬНАЯ РАБОТА
по Статистике:
Вариант №13
2ВО (вечернее)
3 курс (1-й год обучения)
Фак-т: финансово-кредитный
Выполнил:
Проверил:
Теймурова Т.Ю.
Калуга 2008
Задание 1.
По исходным данным таблицы 1:
1.
Постройте статистический ряд распределения организаций
по признаку – среднесписочная
численность работников, образовав, пять групп с равными интервалами.
2.
Постройте графики полученного ряда распределения.
Графически определить значения моды и медианы.
3.
Рассчитайте характеристики ряда распределения: среднюю
арифметическую, среднее квадратическое отклонение, коэффициент вариации.
4.
Вычислите среднюю арифметическую по исходным данным,
сравните его с аналогичным показателем, рассчитанным в п.3 настоящего задания. Объясните
причину их расхождения.
Сделайте
выводы по результатам выполнения задания.
Задание 2.
По
исходным данным табл.1:
1.
Установите наличие и характер связи между признаками –
среднесписочная численность работников и фонд заработной платы:
а)
аналитической группировки,
б)
корреляционной таблицы.
2.
Измерьте тесноту корреляционной связи между названными
признаками с использованием коэффициента детерминации и эмпирического
корреляционного отношения.
Сделайте
выводы.
Задание 3.
По
результатам выполнения задания 1 с вероятностью 0,954 определите:
1.
Ошибку выборки средней списочной численности
работников и границы, в которых будет находиться средняя в генеральной совокупности.
2.
Ошибку выборки доли организаций со средней списочной
численностью работников 180 и более человек и границы, в которых будет
находиться генеральная доля.
Задание 4.
Имеются следующие данные по двум организациям.
|
№ органи-зации
п/п
|
Балансовая прибыль
|
Отчетный период
|
|
Средняя заработная плата,
руб.
|
Среднесписочная
численность работников,
чел.
|
Средняя заработная плата,
руб.
|
Фонд заработной платы,
тыс. руб.
|
|
1
|
5000
|
100
|
6500
|
682,5
|
|
2
|
5600
|
100
|
8000
|
760,0
|
Определите:
1.
Индексы динамики средней заработной платы по каждой
организации
Результаты
расчетов представьте в таблице
2.
По двум организациям вместе:
· Индексы
средней заработной платы переменного, постоянного состава, структурных сдвигов;
· Абсолютное
изменение средней заработной платы в целом и за счет отдельных фактор;
· Абсолютное
изменение фонда заработной платы вследствие изменения среднесписочной
численности работников, средней заработной платы и двух факторов вместе.
Сделайте
выводы.
Имеются следующие выборочные данные по предприятиям
одной из отраслей промышленности в отчетном году (выборка 5%-ная механическая).
Таблица 1
|
№ предприятия
п/п
|
Фонд заработной
платы,
млн.руб.
|
Среднесписочная численность работников,
чел.
|
|
|
|
1
|
2
|
3
|
|
|
1
|
11,340
|
162
|
|
|
2
|
8,112
|
156
|
|
|
3
|
15,036
|
179
|
|
|
4
|
19,012
|
194
|
|
|
5
|
13,035
|
165
|
|
|
6
|
8,532
|
158
|
|
|
7
|
26,400
|
220
|
|
|
8
|
17,100
|
190
|
|
|
9
|
12,062
|
163
|
|
|
10
|
9,540
|
159
|
|
|
11
|
13,694
|
167
|
|
|
12
|
21,320
|
205
|
|
|
13
|
16,082
|
187
|
|
|
14
|
10,465
|
161
|
|
|
15
|
4,320
|
120
|
|
|
16
|
11,502
|
162
|
|
|
17
|
16,356
|
188
|
|
|
18
|
12,792
|
164
|
|
|
19
|
17,472
|
192
|
|
|
20
|
5,850
|
130
|
|
|
21
|
9,858
|
159
|
|
|
22
|
11,826
|
162
|
|
|
23
|
18,142
|
193
|
|
|
24
|
8,848
|
158
|
|
|
25
|
13,944
|
168
|
|
|
26
|
23,920
|
208
|
|
|
27
|
13,280
|
166
|
|
|
28
|
22,356
|
207
|
|
|
29
|
10,948
|
161
|
|
|
30
|
15,810
|
186
|
|
Задание 1
1) Строим статистический ряд распределения организаций
по среднесписочной численности работников.
Построим разработочную таблицу, для этого необходимо
определить величину интервала и
сгруппировать данные по 5 группам:
Определяем интервал
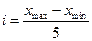
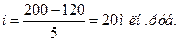
Формируем
группы
|
I
|
120
- 140
|
|
II
|
140
- 160
|
|
III
|
160
- 180
|
|
IV
|
180
- 200
|
|
V
|
200
и выше
|
Значащая
цифра показателя включается в нижнее
значение интервала.
Строим
ряд распределения по среднесписочной численности работников
Разработочная таблица №1
|
№
п/п
|
Группы
предприятий по среднесписочной численности работников
|
Номера
|
Фонд
заработной
платы,
млн.руб.
|
Среднесписочная
численность работников,
чел.
|
|
1
|
120 - 140
|
15,20
|
|
120,130
|
|
 2 2
|
10,170
|
 250 250
|
|
2
|
140 - 160
|
2,6,10,
21,24
|
|
156,158.
159,159,158
|
|
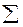 5 5
|
44,890
|
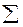 790 790
|
|
3
|
160 - 180
|
1,3,5,9,
11,14,16,
18,22,25,
27,29
|
|
162,179,165,
163,167,161,
162,164,162,
168,166,161
|
|
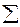 12 12
|
149,924
|
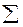 1980 1980
|
|
4
|
180 - 200
|
4,8,13,
17,19,
23,30
|
|
194,190,187,
188,192,
193,186
|
|
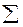 7 7
|
119,974
|
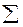 1330 1330
|
|
5
|
200 и выше
|
7,12,
26,28
|
|
220,205,
208,207
|
|
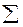 4 4
|
93,996
|
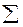 840 840
|
|
ИТОГО:
|
30
|
418,954
|
5190
|
Разработочная таблица №2
|
№
п/п
|
Группы
|
Кол-во
предприятий
|
Удельный
вес, %
|
Кумулята
|
|
1
|
120 - 140
|
2
|
6,666666667
|
2
|
|
2
|
140 - 160
|
5
|
16,66666667
|
7
|
|
3
|
160 - 180
|
12
|
40
|
19
|
|
4
|
180 - 200
|
7
|
23,33333333
|
26
|
|
5
|
200 и выше
|
4
|
13,33333333
|
30
|
|
ИТОГ:
|
30
|
100
|
|
Удельный вес в процентах: 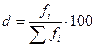
Анализ таблицы 2.
Из данных таблицы 2 следует,
что наибольшее число предприятий 24 или 80% имеют среднесписочную численность
работников от 140
до 200 человек.
Два предприятия или 6,67%
имеют самую маленькую среднесписочную численность работников, и только четыре предприятия или 13,33% имеют среднесписочную численность
работников от
200 и выше человек.
2) Рассчитываем
значение моды и медианы для интервального ряда
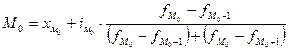
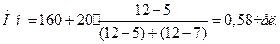
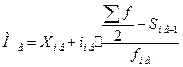
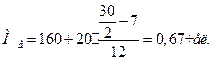
3) Рассчитываем
характеристики ряда распределения: среднюю арифметическую, среднее
квадратическое отклонение, коэффициент вариации.
- среднюю арифметическую:
по взвешенной
арифметической:
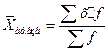
Для
расчета числителя рассчитываем среднюю среднесписочную численность работников
по группе:
|
1)
|
(120+140)/2=
|
130
|
|
2)
|
(140+160)/2=
|
150
|
|
3)
|
(160+180)/2=
|
170
|
|
4)
|
(180+200)/2=
|
190
|
|
5)
|
200
|
200
|
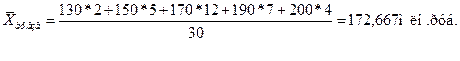
по простой
арифметической:
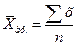
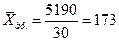
Рассчитываем показатели вариации:
Для этого делаем разработочную таблицу
|
№п/п
|
x
|
f
|

|
|
1
|
130
|
2
|
3640,888889
|
|
2
|
150
|
5
|
2568,888896
|
|
3
|
170
|
12
|
85,33333547
|
|
4
|
190
|
7
|
2103,111111
|
|
5
|
200
|
4
|
2988,444444
|
|
ИТОГО:
|
30
|
11386,66668
|
Среднее квадратическое отклонение
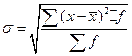
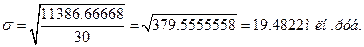
Коэффициент вариации
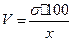
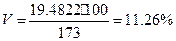
V <
33%. Это свидетельствует о том, что средняя величина – типична и надежна для
данного ряда распределения, а сама совокупность однородна.
4) Вычислим среднюю
арифметическую по исходным данным.
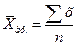
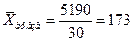
Наиболее
точный результат дает средняя арифметическая простая, равная 173
Разница
в результатах расчета связана с тем, что для простой арифметической берутся
фактические показатели, а при расчете взвешенной арифметической берутся усредненные
показатели по каждой группе.
Задание 2
1) Установим наличие и характер связи между признаками среднесписочная
численность работников и фонд заработной платы.
Для
построения аналитической группировки и установления связи определяем, что
факторным признаком будет среднесписочная численность работников, а
результативным – фонд заработной платы.
Строим
аналитическую группировку, для этого
берем за основу разработочную таблицу №1.
Группировка
предприятий по среднесписочной численности работников
Таблица 3
|
№
п/п
|
Группы
предприятий по среднесписочной численности работников
|
Количество
предприятий
|
Среднесписочная
численность работников, чел.
|
Фонд
заработной
платы,
млн.руб.
|
|
всего
|
На одно предприятие
|
всего
|
На одно предприятие
|
|
1
|
120 - 140
|
2
|
250
|
125
|
10,170
|
5,085
|
|
2
|
140 - 160
|
5
|
790
|
158
|
44,890
|
8,978
|
|
3
|
160 - 180
|
12
|
1980
|
165
|
149,924
|
13,494
|
|
4
|
180 - 200
|
7
|
1330
|
190
|
119,974
|
17,139
|
|
5
|
200 и выше
|
4
|
840
|
210
|
93,996
|
23,499
|
|
ИТОГО:
|
30
|
5190
|
848
|
418,954
|
68,195
|
|
|
|
|
173
|
|
13,96
|
Для анализа таблицы делаем расчет интенсивности роста
показателей в среднем на 1 предприятие от первой к пятой группе:
определяем
коэффициент роста по фонду заработной платы
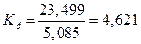
определяем коэффициент роста по среднесписочной численности
работников
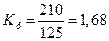
Анализ
(см.лекции)
С
увеличением фонда заработной платы растет и среднесписочная численность
работников – это говорит о наличии прямой связи между указанными признаками.
Из данных таблицы 3 видно, что фонд заработной платы от
первой к пятой группе растет быстрее, чем увеличивается среднесписочная
численность работников, это свидетельствует о наличии корреляционной связи
между рассмотренными показателями.
2) Измерим тесноту корреляционной связи между названными признаками с
использованием коэффициента детерминации и эмпирического корреляционного
отношения
Для
измерения корреляционной связи необходимо рассчитать межгрупповую и общую дисперсии:
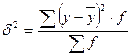
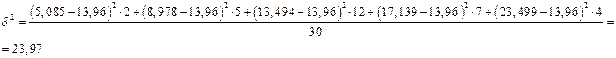
Общая дисперсия
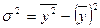
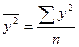
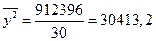
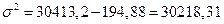
Коэффициент детерминации:
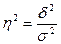
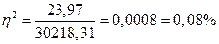
Коэффициент
детерминации свидетельствует о том, что среднесписочная численность работников
предприятия на 0,08% зависит от фонда заработной платы.
Эмпирическое корреляционное
соотношение:
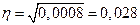
Из
соотношения Чеддока:
0,9<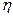 <0.99 следовательно, связь между признаками весьма тесная.
<0.99 следовательно, связь между признаками весьма тесная.
Задание 3
1)
Определяем ошибку выборки среднесписочной численности работников и границы, в
которых будет находиться средняя в генеральной совокупности.
Данные
являются 5% механической выборкой, p=0,954:
Из
задания 1: 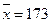
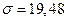
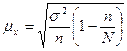
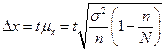
n=30
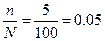
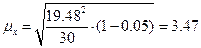 тыс. руб.
тыс. руб.
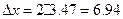
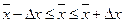
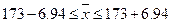
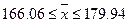
Вывод:
с вероятностью 0,954 можно утверждать, что средний фонд заработной платы организации будет
находиться в пределах от 166,06 до 179,94 млн. руб.
2) Определяем ошибку выборки доли организаций со среднесписочной
численностью работников 180 и более человек и границы, в которых будет
находиться генеральная доля.
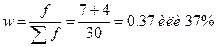
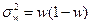
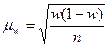
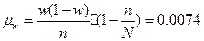
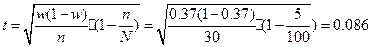
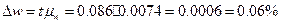
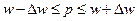
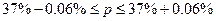
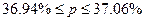
Вывод:
с вероятностью 0,954 можно утверждать, что доля организаций со среднесписочной
численностью работников 180 и более человек будет находиться в пределах от
36,94% до 37,06 % для всех организаций.