Министерство образования и науки
РФ
Федеральное агентство по
образованию ГОУ ВПО
Всероссийский заочный
финансово-экономический институт
Кафедра бух. учета, аудита и
статистики
Контрольная работа
по дисциплине:
«Статистика»
Вариант № 18
Содержание
Задание 1. Исследование структуры совокупности. 3
Задание 2. Выявление наличия корреляционной связи между признаками,
установление направления связи и измерение ее тесноты. 10
Задание 3. Применение выборочного метода в
финансово-экономических задачах. 16
Задание 4. Использование рядов динамики в финансово-экономических
задачах 19
Литература. 22
Имеются следующие выборочные данные о деятельности коммерческих банков (выборка
5%-ная механическая), млн. руб.:
Таблица 1
Исходные данные
|
№ банка п/п
|
Прибыль
|
Собственный капитал
|
|
1
|
170
|
3900
|
|
2
|
200
|
4500
|
|
3
|
150
|
3000
|
|
4
|
90
|
2300
|
|
5
|
130
|
3700
|
|
6
|
170
|
3200
|
|
7
|
155
|
3780
|
|
8
|
190
|
4000
|
|
9
|
180
|
3100
|
|
10
|
210
|
4600
|
|
11
|
100
|
2200
|
|
12
|
220
|
5280
|
|
13
|
250
|
4700
|
|
14
|
180
|
4400
|
|
15
|
276
|
6500
|
|
16
|
220
|
5000
|
|
17
|
140
|
2500
|
|
18
|
50
|
1800
|
|
19
|
190
|
4200
|
|
20
|
210
|
5600
|
|
21
|
346
|
7962
|
|
22
|
240
|
5850
|
|
23
|
120
|
400
|
|
24
|
230
|
4900
|
|
25
|
350
|
8400
|
|
26
|
280
|
7088
|
|
27
|
163
|
5100
|
|
28
|
200
|
4300
|
|
29
|
260
|
6020
|
|
30
|
270
|
4800
|
Задание 1. Исследование структуры
совокупности
1. Постройте
статистический ряд распределения коммерческих банков по признаку – прибыль,
образовав, пять групп с равными интервалами.
2. Постройте
графики полученного ряда распределения. Графически определите значения моды и
медианы.
3. Рассчитайте
характеристики интервального ряда распределения: среднюю арифметическую,
среднее квадратическое отклонение, коэффициент вариации, моду и медиану.
4. Вычислите
среднюю арифметическую по исходным данным, сравните ее с аналогичным показателем,
рассчитанным в п. 3 для интервального ряда распределения.
Сделайте выводы по результатам выполнения задания.
Решение:
1.
Постройте
статистический ряд распределения коммерческих банков по признаку – прибыль,
образовав, пять групп с равными интервалами.
По колонке «Прибыль» построим интервальный вариационный ряд. Для
построения интервального ряда распределения определим величину интервала h по формуле:
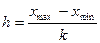 ,
,
где
xmax и xmin – максимальное и минимальное
значение признака, k – число групп.
При заданных 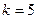 ,
, 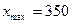 ,
, 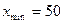 величина интервала
равна:
величина интервала
равна:
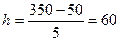 (млн. руб.).
(млн. руб.).
При 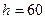 определим границы интервалов ряда распределения (табл.
2).
определим границы интервалов ряда распределения (табл.
2).
Таблица 2
Границы интервалов ряда распределения
|
Номер группы
|
Нижняя граница,
млн. руб.
|
Верхняя граница,
млн. руб.
|
|
1
|
50
|
110
|
|
2
|
110
|
170
|
|
3
|
170
|
230
|
|
4
|
230
|
290
|
|
5
|
290
|
350
|
Для
определения числа коммерческих банков в каждой группе строим разработочную таблицу
3.
Таблица 3
Разработочная таблица для построения
интервального ряда распределения и
аналитической
группировки
|
№ банка п/п
|
Группы банков по прибыли
|
Прибыль, млн. руб. (Х)
|
Собственный капитал, млн. руб.
|
|
1
|
2
|
3
|
4
|
|
1
|
50-110
|
50
|
1800
|
|
90
|
2300
|
|
100
|
2200
|
|
Всего
|
3
|
240
|
6300
|
|
2
|
110-170
|
120
|
400
|
|
130
|
3700
|
|
140
|
2500
|
|
150
|
3000
|
|
155
|
3780
|
|
163
|
5100
|
|
Всего
|
6
|
858
|
18480
|
|
3
|
170-230
|
170
|
3900
|
|
170
|
3200
|
|
180
|
3100
|
|
180
|
4400
|
|
190
|
4000
|
|
190
|
4200
|
|
200
|
4500
|
|
200
|
4300
|
|
210
|
4600
|
|
210
|
5600
|
|
220
|
5280
|
|
220
|
5000
|
|
Всего
|
12
|
2340
|
52080
|
|
4
|
230-290
|
230
|
4900
|
|
240
|
5850
|
|
250
|
4700
|
|
260
|
6020
|
|
270
|
4800
|
|
276
|
6500
|
|
280
|
7088
|
|
Всего
|
7
|
1806
|
39858
|
|
5
|
290-350
|
346
|
7962
|
|
350
|
8400
|
|
Всего
|
2
|
696
|
16362
|
|
Итого
|
30
|
5940
|
133 080
|
На основе групповых итоговых строк «Всего» формируем итоговую таблицу 4,
представляющую интервальный ряд распределения коммерческих банков по прибыли.
Таблица 4
Распределение коммерческих банков по прибыли
|
Номер группы
|
Группы банков по прибыли, млн.руб..,
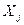
|
Частота (fj) Число банков, ед.,
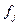
|
Доля банков в общем итоге (частость),
wj
|
Накопленная частота,
Sj
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
50-110
|
3
|
0,100
|
3
|
|
2
|
110-170
|
6
|
0,2
|
9
|
|
3
|
170-230
|
12
|
0,4
|
21
|
|
4
|
230-290
|
7
|
0,233
|
28
|
|
5
|
290-350
|
2
|
0,067
|
30
|
|
Итого
|
30
|
1
|
|
Вывод: Анализ интервального
ряда распределения изучаемой совокупности коммерческих банков показывает, что
распределение банков по прибыли не является равномерным: преобладают банки с
уровнем прибыли от 170 до 230 млн. руб. (12 банков, доля которых составляет
40%); самая малочисленная группа коммерческих банков имеет прибыль от 290 до 350
млн. руб., которая включает 2 банка, что составляет 6,6% от общего числа коммерческих
банков.
2.
Постройте
графики полученного ряда распределения. Графически определите значения моды и
медианы.
Для определения моды
графическим методом строим по данным таблицы 4 (графы 2 и 3) гистограмму
распределения коммерческих банков по изучаемому признаку (рис. 1).





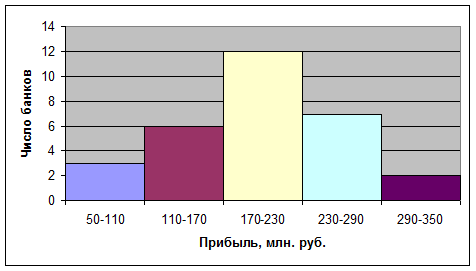
Рис. 1.
Гистограмма распределения организаций по уровню цен
Для определения медианы
графическим методом строим по данным таблицы 4 (графы 2 и 5) кумуляту
распределения банков по изучаемому признаку (рис. 2).



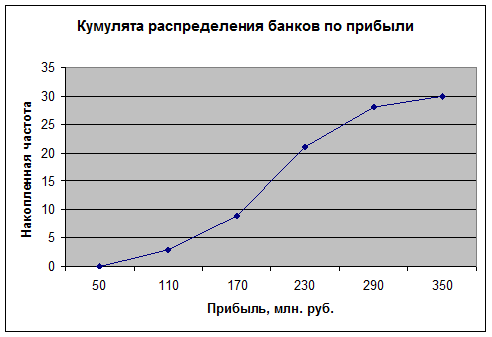
Рис. 2. Определение медианы графическим
методом
3.
Рассчитайте
характеристики интервального ряда распределения: среднюю арифметическую,
среднее квадратическое отклонение, коэффициент вариации, моду и медиану.
Мода 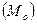 – значение признака,
повторяющееся в выборке с наибольшей частотой.
– значение признака,
повторяющееся в выборке с наибольшей частотой.
Определим модальный интервал, используя табл. 4 (графы 2 и 3). Наибольшее
число коммерческих банков – 12, имеют прибыль от 170 до 230 млн. руб.
Следовательно, этот интервал является модальным интервалом ряда распределения.
Определим значение моды по формуле:
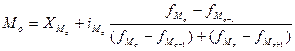 ,
,
где  – нижняя граница
модального интервала (
– нижняя граница
модального интервала (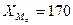 );
);
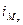 – величина модального
интервала (
– величина модального
интервала (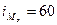 );
);
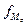 – частота модального
интервала (
– частота модального
интервала (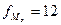 );
);
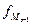 – частота интервала,
предшествующая модальному интервалу (
– частота интервала,
предшествующая модальному интервалу (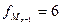 );
);
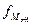 – частота интервала,
последующая за модальным интервалом (
– частота интервала,
последующая за модальным интервалом (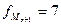 ).
).
Подставляя данные в формулу, найдем:
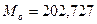 (млн. руб.).
(млн. руб.).
Вывод: Большинство коммерческих банков имеют прибыль,
равную 202,727 млн. руб.
Медиана 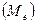 – значение признака,
приходящееся на середину ранжированного ряда выборочных данных.
– значение признака,
приходящееся на середину ранжированного ряда выборочных данных.
Определяем медианный интервал, используя табл. 4 (графы 2 и 5). Сумма накопленных частот,
превышающая половину всех значений 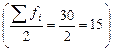 , соответствует интервалу 170 – 230 млн. руб. Это и
есть медианный интервал, в котором находится медиана. Определим ее значение по
формуле:
, соответствует интервалу 170 – 230 млн. руб. Это и
есть медианный интервал, в котором находится медиана. Определим ее значение по
формуле:
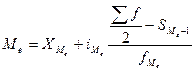 ,
,
где
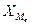 – нижняя граница
медианного интервала (
– нижняя граница
медианного интервала (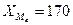 )
)
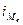 – величина медианного
интервала (
– величина медианного
интервала (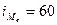 ),
),
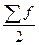 – половина суммы
частот ряда
– половина суммы
частот ряда 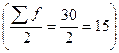
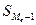 – сумма накопленных
частот, предшествующих медианному интервалу (
– сумма накопленных
частот, предшествующих медианному интервалу (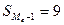 );
);
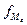 – частота медианного
интервала (
– частота медианного
интервала (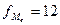 ).
).
Следовательно, 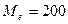 (млн. руб.).
(млн. руб.).
Вывод: Первая
половина исследуемых коммерческих банков имеют прибыль до 200 млн. руб., а
другая половина свыше 200 млн. руб.
Для расчета характеристик ряда распределения средней
арифметической, среднего квадратического отклонения, коэффициента вариации на
основе табл. 4 строим вспомогательную таблицу 5 (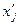 - середина интервалов).
- середина интервалов).
Таблица 5
Расчетная таблица для нахождения
характеристик ряда распределения
|
Номер
группы
|
Группы
банков по прибыли, млн.руб..,
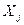
|
Частота
(fj) Число банков, ед.,
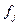
|
Накопленная
частота
|
Середина
интервала (X/j)
|
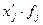
|
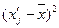
|
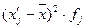
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
50-110
|
3
|
3
|
80
|
240
|
13924,00
|
41772
|
|
2
|
110-170
|
6
|
9
|
140
|
840
|
3364,00
|
20184
|
|
3
|
170-230
|
12
|
21
|
200
|
2400
|
4,00
|
48
|
|
4
|
230-290
|
7
|
28
|
260
|
1820
|
3844,00
|
26908
|
|
5
|
290-350
|
2
|
30
|
320
|
640
|
14884,00
|
29768
|
|
Итого
|
30
|
|
|
5940
|
|
118680,0
|
Рассчитаем
среднюю арифметическую взвешенную:
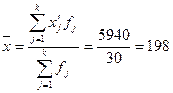 (млн. руб.).
(млн. руб.).
Определим дисперсию 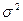 выборочной совокупности:
выборочной совокупности:
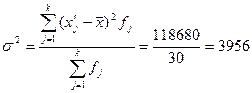
Рассчитаем среднее квадратическое отклонение 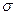 :
:
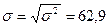 (млн. руб.).
(млн. руб.).
Найдем размах вариации (R), устанавливающий
предельное значение амплитуды колебаний признака:
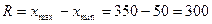 .
.
Рассчитаем
коэффициент вариации:
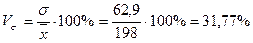
Вывод: Анализ полученных значений показателей 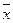 и
и 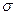 говорит о том, что
средняя величина прибыли банков составляет 198 млн. руб., отклонение от этой
величины в ту или иную сторону составляет в среднем 62,9 млн. руб. (или 31,77%),
наиболее характерный уровень прибыли находится в пределах от 135,1 до 260,9 млн.
руб. (диапазон
говорит о том, что
средняя величина прибыли банков составляет 198 млн. руб., отклонение от этой
величины в ту или иную сторону составляет в среднем 62,9 млн. руб. (или 31,77%),
наиболее характерный уровень прибыли находится в пределах от 135,1 до 260,9 млн.
руб. (диапазон 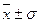 ).
).
Значение 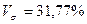 не превышает 33%,
следовательно, вариация прибыли в исследуемой совокупности коммерческих банков
незначительна и совокупность по данному признаку однородна. Расхождение между
значениями
не превышает 33%,
следовательно, вариация прибыли в исследуемой совокупности коммерческих банков
незначительна и совокупность по данному признаку однородна. Расхождение между
значениями 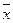 ,
, 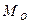 и
и 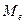 незначительно (
незначительно (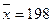 млн. руб.,
млн. руб., 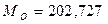 млн. руб.,
млн. руб., 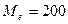 млн. руб.), что
подтверждает вывод об однородности совокупности коммерческих банков. Таким
образом, найденное среднее значение уровня прибыли (198 млн. руб.) является
типичной, надежной характеристикой исследуемой совокупности банков.
млн. руб.), что
подтверждает вывод об однородности совокупности коммерческих банков. Таким
образом, найденное среднее значение уровня прибыли (198 млн. руб.) является
типичной, надежной характеристикой исследуемой совокупности банков.
4.
Вычислите
среднюю арифметическую по исходным данным, сравните ее с аналогичным
показателем, рассчитанным в п. 3 для интервального ряда распределения.
Для расчета средней
арифметической по исходным данным применяется формула средней
арифметической простой:
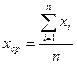 ,
,
где
xi – значение
признака,
n –
число коммерческих банков.
Следовательно,
 (млн. руб.).
(млн. руб.).
Вывод: Средняя арифметическая по исходным данным и для
интервального ряда распределения равна 198 млн. руб.
Задание 2. Выявление наличия
корреляционной связи между признаками, установление направления связи и измерение
ее тесноты.
По исходным данным (табл. 1):
1. Установите
наличие и характер связи между признаками прибыль и собственный капитал,
образовав заданное одинаковое число групп по обоим признакам с равными
интервалами, методами:
а)
аналитической группировки;
б)
корреляционной таблицы.
2. Измерьте
тесноту корреляционной связи между признаками с использованием коэффициента
детерминации и эмпирического корреляционного отношения.
Сделайте выводы по результатам выполнения задания.
Решение:
По условию задания 2 факторным является признак Прибыль, результативным – признак Собственный капитал.
1.
Установите
наличие и характер связи между признаками прибыль
и собственный
капитал, образовав заданное
одинаковое число групп по обоим признакам с равными интервалами.
а)
Применение
метода аналитической группировки.
Аналитическая группировка строится
по факторному признаку Х и для каждой
j-ой группы ряда определяется среднегрупповое значение 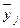 результативного
признака Y. Если с ростом значений фактора Х от группы к группе средние значения
результативного
признака Y. Если с ростом значений фактора Х от группы к группе средние значения 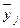 систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
Используя разработочную таблицу 3,
строим аналитическую группировку, характеризующую зависимость между факторным
признаком Х – Прибыль и
результативным признаком Y –
Собственный
капитал. Макет аналитической таблицы имеет следующий вид (табл. 6):
Таблица 6
Макет аналитической таблицы
|
Номер группы
|
Группы банков по прибыли, млн. руб.
X
|
Число банков, 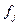
|
Собственный капитал, млн. руб.
|
|
Всего
|
в среднем на один банк, 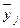
|
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итого
|
|
|
|
Групповые средние значения 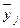 получаем из
таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную
аналитическую группировку представляет табл. 7:
получаем из
таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную
аналитическую группировку представляет табл. 7:
Таблица 7
Зависимость собственного капитала от прибыли
|
№ группы
|
Группы банков по прибыли, млн. руб.
млн.руб.,
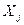
|
Число банков,
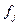
|
Собственный капитал, млн. руб.
|
|
Всего
|
На один банк, 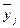
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
50-110
|
3
|
6 300
|
2 100
|
|
2
|
110-170
|
6
|
18 480
|
3 080
|
|
3
|
170-230
|
12
|
52 080
|
4 340
|
|
4
|
230-290
|
7
|
39 858
|
5 694
|
|
5
|
290-350
|
2
|
16 362
|
8 181
|
|
Итого
|
30
|
133 080
|
4 436
|
Вывод: Анализ
данных таблицы 7 показывает, что по мере увеличения 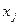 увеличиваются
значения
увеличиваются
значения 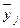 , следовательно, можно
говорить, что чем больше прибыль, тем больше собственный капитал, что
свидетельствует о наличии прямой корреляционной связи между исследуемыми
признаками.
, следовательно, можно
говорить, что чем больше прибыль, тем больше собственный капитал, что
свидетельствует о наличии прямой корреляционной связи между исследуемыми
признаками.
б)
Применение
метода корреляционных таблиц.
Корреляционная таблица строится как комбинация двух рядов распределения
по факторному признаку Х и
результативному признаку Y. На пересечении j-ой строки и k-ой графы таблицы указывается
число единиц совокупности, входящих в j-ый интервал по признаку
X и в k-ый
интервал по признаку Y.
Концентрация частот около диагонали построенной таблицы свидетельствует о
наличии корреляционной связи между признаками – прямой или обратной. Связь прямая,
если частоты располагаются по диагонали, идущей от левого верхнего угла к
правому нижнему, обратная – по диагонали от правого верхнего угла к левому
нижнему.
Для построения корреляционной таблицы необходимо знать величины и границы
интервалов по двум признакам X и Y. Для факторного признака Х
– Прибыль эти величины известны из табл. 3 Определяем величину интервала для
результативного признака Y – Собственный капитал при 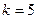 ,
, 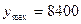 (млн. руб.),
(млн. руб.), 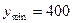 (млн. руб.):
(млн. руб.):
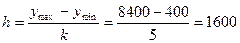 (млн. руб.).
(млн. руб.).
При 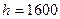 определим границы интервалов ряда распределения
результативного признака Y (табл. 8).
определим границы интервалов ряда распределения
результативного признака Y (табл. 8).
Таблица 8
Границы
интервалов ряда распределения
|
Номер группы
|
Нижняя граница,
млн. руб.
|
Верхняя граница,
млн. руб..
|
|
1
|
400
|
2000
|
|
2
|
2000
|
3600
|
|
3
|
3600
|
5200
|
|
4
|
5200
|
6800
|
|
5
|
6800
|
8400
|
Подсчитывая для каждой группы число входящих в нее банков, получаем интервальный
ряд распределения результативного признака (табл. 9).
Таблица 9
Интервальный ряд распределения банков по собственному
капиталу
|
Группы банков по собственному
капиталу,
млн. руб.,
Y
|
Число Банков
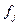 . .
|
|
400-2000
|
2
|
|
2000-3600
|
6
|
|
3600-5200
|
14
|
|
5200-6800
|
5
|
|
6800-8400
|
3
|
|
ИТОГО
|
30
|
Используя группировки по факторному и результативному признакам, строим
корреляционную таблицу (табл. 10).
Таблица 10
Корреляционная таблица зависимости собственного
капитала от прибыли
|
Группы Банков по
прибыли,
млн. руб.
|
Группы Банков по
собственному капиталу, млн. руб.
|
ИТОГО
|
|
400-2000
|
2000-3600
|
3600-5200
|
5200-6800
|
6800-8400
|
|
50-110
|
1
|
2
|
|
|
|
3
|
|
110-170
|
1
|
2
|
3
|
|
|
6
|
|
170-230
|
|
2
|
8
|
2
|
|
12
|
|
230-290
|
|
|
3
|
3
|
1
|
7
|
|
290-350
|
|
|
|
|
2
|
2
|
|
Итого
|
2
|
6
|
14
|
5
|
3
|
30
|
Вывод: Анализ данных табл. 10 показывает, что
распределение частот групп произошло вдоль диагонали, идущей из левого верхнего
угла в правый нижний угол таблицы. Это свидетельствует о наличии прямой
корреляционной связи между прибылью и собственным капиталом.
2.
Измерьте
тесноту корреляционной связи между признаками с использованием коэффициента
детерминации и эмпирического корреляционного отношения.
Коэффициент детерминации 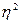 характеризует
силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как
доля межгрупповой дисперсии
характеризует
силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как
доля межгрупповой дисперсии 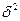 в общей дисперсии
в общей дисперсии 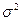 результативного
признака:
результативного
признака:
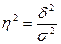 ,
,
где 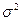 – общая дисперсия признака Y,
– общая дисперсия признака Y,
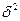 – межгрупповая (факторная) дисперсия признака Y.
– межгрупповая (факторная) дисперсия признака Y.
Общая дисперсия 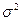 характеризует вариацию
результативного признака, сложившуюся под влиянием всех действующих на Y
факторов (систематических и случайных)
и вычисляется по формуле:
характеризует вариацию
результативного признака, сложившуюся под влиянием всех действующих на Y
факторов (систематических и случайных)
и вычисляется по формуле:
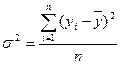 ,
,
где 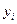 – индивидуальные
значения результативного признака;
– индивидуальные
значения результативного признака;
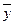 – общая средняя значений результативного
признака Y;
– общая средняя значений результативного
признака Y;
n – число единиц
совокупности.
Межгрупповая
дисперсия 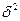 измеряет систематическую вариацию результативного признака,
обусловленную влиянием
признака-фактора Х (по
которому произведена группировка) и вычисляется по формуле:
измеряет систематическую вариацию результативного признака,
обусловленную влиянием
признака-фактора Х (по
которому произведена группировка) и вычисляется по формуле:
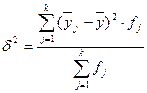 ,
,
где 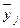 – групповые средние;
– групповые средние;
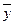 – общая средняя признака Y;
– общая средняя признака Y;
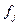 – число единиц в j-ой группе;
– число единиц в j-ой группе;
k – число выделенных групп.
Для расчета показателей 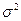 и
и 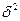 необходимо знать
величину общей средней
необходимо знать
величину общей средней
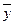 , которая вычисляется как средняя
арифметическая простая по всем единицам совокупности:
, которая вычисляется как средняя
арифметическая простая по всем единицам совокупности:
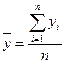 .
.
Значения числителя и знаменателя формулы имеются в табл. 7 (графы 3 и 4
итоговой строки). Используя эти данные, получаем общую среднюю 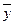 :
:
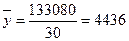 (млн. руб.).
(млн. руб.).
Для расчета общей дисперсии 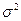 применяется
вспомогательная таблица 11.
применяется
вспомогательная таблица 11.
Таблица 11
Вспомогательная
таблица для расчета общей дисперсии
|
№ банка п/п
|
Прибыль, млн. руб. (Х)
|
Собственный капитал, млн.
руб.,
(Y)
|
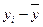 . .
|
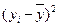
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
50
|
1800
|
-2 636
|
6 948 496
|
|
2
|
90
|
2300
|
-2 136
|
4 562 496
|
|
3
|
100
|
2200
|
-2 236
|
4 999 696
|
|
4
|
120
|
400
|
-4 036
|
16 289 296
|
|
5
|
130
|
3700
|
-736
|
541 696
|
|
6
|
140
|
2500
|
-1 936
|
3 748 096
|
|
7
|
150
|
3000
|
-1 436
|
2 062 096
|
|
8
|
155
|
3780
|
-656
|
430 336
|
|
9
|
163
|
5100
|
664
|
440 896
|
|
10
|
170
|
3900
|
-536
|
287 296
|
|
11
|
170
|
3200
|
-1 236
|
1 527 696
|
|
12
|
180
|
3100
|
-1 336
|
1 784 896
|
|
13
|
180
|
4400
|
-36
|
1 296
|
|
14
|
190
|
4000
|
-436
|
190 096
|
|
15
|
190
|
4200
|
-236
|
55 696
|
|
16
|
200
|
4500
|
64
|
4 096
|
|
17
|
200
|
4300
|
-136
|
18 496
|
|
18
|
210
|
4600
|
164
|
26 896
|
|
19
|
210
|
5600
|
1 164
|
1 354 896
|
|
20
|
220
|
5280
|
844
|
712 336
|
|
21
|
220
|
5000
|
564
|
318 096
|
|
22
|
230
|
4900
|
464
|
215 296
|
|
23
|
240
|
5850
|
1 414
|
1 999 396
|
|
24
|
250
|
4700
|
264
|
69 696
|
|
25
|
260
|
6020
|
1 584
|
2 509 056
|
|
26
|
270
|
4800
|
364
|
132 496
|
|
27
|
276
|
6500
|
2 064
|
4 260 096
|
|
28
|
280
|
7088
|
2 652
|
7 033 104
|
|
29
|
346
|
7962
|
3 526
|
12 432 676
|
|
30
|
350
|
8400
|
3 964
|
15 713 296
|
|
Итого
|
5 940
|
133 080
|
-
|
90 670 008
|
Рассчитаем общую дисперсию:
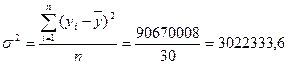 .
.
Для расчета межгрупповой дисперсии 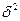 строится вспомогательная
таблица 12. При этом используются
групповые средние значения
строится вспомогательная
таблица 12. При этом используются
групповые средние значения 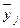 из табл. 7 (графа 5).
из табл. 7 (графа 5).
Таблица 12
Вспомогательная таблица для расчета
межгрупповой дисперсии
|
Группы банков по прибыли, млн.руб.
Хj
|
Число банков, ед.
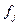
|
Среднее значение в группе, кг.,
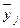
|
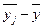 . .
|
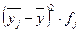
|
|
1
|
2
|
3
|
4
|
5
|
|
50-110
|
3
|
2 100
|
-2 336
|
16 370 688
|
|
110-170
|
6
|
3 080
|
-1 356
|
11 032 416
|
|
170-230
|
12
|
4 340
|
-96
|
110 592
|
|
230-290
|
7
|
5 694
|
1 258
|
11 077 948
|
|
290-350
|
2
|
8 181
|
3 745
|
28 050 050
|
|
Итого
|
30
|
-
|
-
|
66 641 694
|
Рассчитаем
межгрупповую дисперсию:
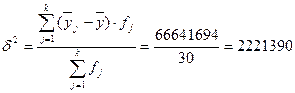 .
.
Определим коэффициент детерминации:
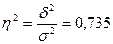 или
или 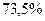 .
.
Эмпирическое корреляционное отношение 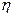 оценивает тесноту связи между факторным
(группировочным) и результативным признаками и вычисляется по формуле:
оценивает тесноту связи между факторным
(группировочным) и результативным признаками и вычисляется по формуле:
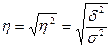 .
.
Рассчитаем показатель 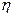 :
:
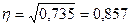 .
.
Вывод: Коэффициент детерминации показывает,
что на 73,5 % вариация собственного капитала обусловлена различиями в прибыли и
на 26,5 % - влиянием прочих факторов.
Поскольку эмпирическое корреляционное отношение равно 0,735, (0,7 <
0,735 <0,9), следовательно, по шкале Чэддока связь между прибылью и
собственным капиталом является тесной.
Задание 3. Применение
выборочного метода в финансово-экономических задачах
По результатам выполнения задания 1 с вероятностью 0,683 определите:
1. Ошибку
выборки средней прибыли и границы, в которых будет находиться средний размер
прибыли в генеральной совокупности.
2. Ошибку
выборки доли банков с прибылью 230 и более млн. руб. и границы, в которых будет
находиться генеральная доля.
Решение:
1.
С
вероятностью 0,683 определить ошибку выборки средней прибыли и границы, в
которых будет находиться средний размер прибыли в генеральной совокупности.
Применяя выборочный метод наблюдения, необходимо рассчитать ошибки
выборки (ошибки репрезентативности), т.к. генеральные и выборочные
характеристики, как правило, не совпадают, а отклоняются на некоторую величину 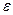 .
.
Принято вычислять два вида ошибок выборки – среднюю  и предельную
и предельную 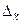 .
.
Для расчета средней ошибки выборки  применяются различные формулы в зависимости от
вида и способа отбора единиц из генеральной совокупности в выборочную.
применяются различные формулы в зависимости от
вида и способа отбора единиц из генеральной совокупности в выборочную.
Для собственно-случайной и механической
выборки с бесповторным способом отбора
средняя ошибка  для выборочной средней
для выборочной средней 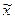 определяется по
формуле:
определяется по
формуле:
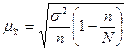 ,
,
где 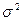 – общая дисперсия
изучаемого признака;
– общая дисперсия
изучаемого признака;
N – число единиц в генеральной совокупности;
n – число единиц в выборочной совокупности.
Предельная ошибка выборки для
средней 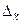 определяет границы, в пределах которых
будет находиться генеральная средняя:
определяет границы, в пределах которых
будет находиться генеральная средняя:
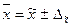 ,
,
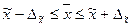 ,
,
где 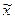 – выборочная средняя,
– выборочная средняя,
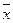 – генеральная средняя.
– генеральная средняя.
Предельная ошибка выборки 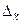 кратна средней ошибке
кратна средней ошибке  с коэффициентом кратности t (коэффициентом доверия):
с коэффициентом кратности t (коэффициентом доверия):
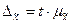 .
.
Коэффициент кратности t
зависит от значения доверительной вероятности p, гарантирующей
вхождение генеральной средней в интервал
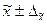 , называемый доверительным интервалом.
, называемый доверительным интервалом.
Наиболее часто используемые доверительные вероятности p и соответствующие им значения t задаются следующим образом (табл. 15):
Таблица 13
Значения функции Лапласа
|
Доверительная
вероятность p
|
0,683
|
0,866
|
0,954
|
0,988
|
0,997
|
0,999
|
|
Значение t
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
По условию выборочная совокупность насчитывает 30 банков, выборка 5%-ная
механическая, следовательно, генеральная
совокупность включает 600 банков. Выборочная средняя 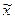 , дисперсия
, дисперсия 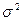 определены в задании 1 (п. 3). Значения параметров,
необходимых для решения задачи, представлены в табл. 14.
определены в задании 1 (п. 3). Значения параметров,
необходимых для решения задачи, представлены в табл. 14.
Таблица 14
Вспомогательная таблица для определения средней ошибки выборки, предельной
ошибки выборки, доверительного интервала
|
p
|
t
|
n
|
N
|
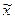
|
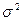
|
|
0,683
|
1
|
30
|
600
|
198
|
3956
|
Рассчитаем среднюю ошибку выборки:
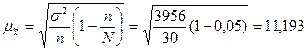 (млн. руб.).
(млн. руб.).
Рассчитаем предельную ошибку выборки для средней:
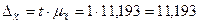 (млн. руб.).
(млн. руб.).
Определим доверительный интервал для генеральной средней:
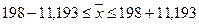
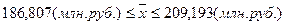 .
.
Вывод. На основании проведенного
выборочного обследования с вероятностью 0,683 можно утверждать, что для
генеральной совокупности коммерческих банков средняя величина прибыли находится
в пределах от 186,807 до 209,193 млн. руб.
2.
С
вероятностью 0,683 определить ошибку выборки доли банков с прибылью 230 и более
млн. руб. и границы, в которых будет находиться генеральная доля.
Доля единиц выборочной совокупности, обладающих тем или иным заданным
свойством, выражается формулой:
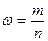 ,
,
где m – число единиц совокупности, обладающих заданным свойством;
n – общее число единиц в выборочной
совокупности.
Для собственно-случайной и механической
выборки с бесповторным
способом отбора предельная ошибка выборки 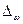 доли единиц,
обладающих заданным свойством, рассчитывается по формуле:
доли единиц,
обладающих заданным свойством, рассчитывается по формуле:
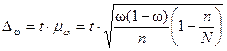 ,
,
где 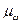 – средняя ошибка
выборки для доли;
– средняя ошибка
выборки для доли;
t –
нормированное отклонение (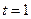 , т.к.
, т.к. 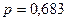 );
);
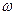 – доля
единиц совокупности, обладающих заданным свойством;
– доля
единиц совокупности, обладающих заданным свойством;
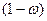 – доля единиц
совокупности, не обладающих заданным свойством,
– доля единиц
совокупности, не обладающих заданным свойством,
N – число единиц в генеральной совокупности,
n – число единиц в выборочной
совокупности.
Предельная ошибка выборки 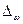 определяет границы, в пределах которых
будет находиться генеральная доля р единиц, обладающих исследуемым
признаком:
определяет границы, в пределах которых
будет находиться генеральная доля р единиц, обладающих исследуемым
признаком:
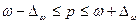 .
.
По условию задания 3 исследуемым свойством банков является равенство или превышение прибыли величины 230
млн. руб.
Число банков с данным свойством определяется из табл. 3 (графа 3):
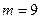 .
.
Рассчитаем выборочную долю:
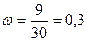 .
.
Рассчитаем предельную ошибку выборки для доли:
 .
.
Определим доверительный интервал генеральной доли:
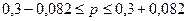 ;
;
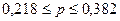 или
или 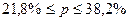 .
.
Вывод: С
вероятностью 0,683 можно утверждать, что в генеральной совокупности коммерческих
банков доля банков с прибылью 230 млн. руб. и более будет находиться в
пределах от 21,8% до 38,2%.
Задание
4. Использование рядов динамики в финансово-экономических задачах
Имеются следующие данные о динамике задолженности
организаций по кредитам банков (табл. 15):
Таблица15
Данные о задолженности
организаций по кредитам банков
|
Год
|
Задолженность
по кредитам, млрд. руб.
|
|
1
|
960
|
|
2
|
1800
|
|
3
|
2400
|
|
4
|
3500
|
|
5
|
4200
|
Определите:
1.
Среднегодовую задолженность организаций по
кредиту.
2.
Абсолютные и относительные изменения
задолженности (цепные и базисные абсолютные приросты, темпы роста, темпы
прироста).
Рассчитанные показатели представить в таблице.
3.
Среднегодовые темпы роста и прироста
задолженности.
4.
Осуществить прогноз задолженности организаций по
кредитам банков при условии, что среднегодовой темп сохранится на прежнем
уровне еще в течение двух лет.
5.
Постройте график динамики задолженности
Сделайте выводы.
Решение:
1.
Среднегодовая задолженность организаций по кредиту, млрд. руб.:
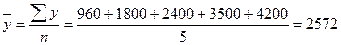 .
.
2.
Абсолютные и относительные изменения задолженности:
Абсолютное изменение характеризует
увеличение или уменьшение уровня ряда за определенный промежуток времени.
Абсолютный прирост с переменной базой называют скоростью роста.
Абсолютный
прирост (цепной): 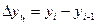 , абсолютный прирост
(базисный):
, абсолютный прирост
(базисный): 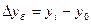 ,
,
где
yi – уровень
сравниваемого периода;
yi-1 – уровень предшествующего периода;
y0 – уровень базисного периода.
Для характеристики интенсивности, т.е. относительного
изменения уровня динамического ряда за какой-либо период времени исчисляют темпы
роста (снижения).
Темп роста
(цепной): 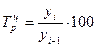 , темп роста
(базисный):
, темп роста
(базисный): 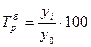 .
.
Относительную оценку скорости
измерения уровня ряда в единицу времени дают показатели темпа прироста
(сокращения).
Темп прироста (сокращения) показывает,
на сколько процентов сравниваемый уровень больше или меньше уровня, принятого
за базу сравнения.
Темп прироста
(цепной): 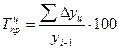 , темп прироста
(базисный):
, темп прироста
(базисный):  .
.
Рассчитанные показатели представим в таблице 16.
Таблица16
Динамика
задолженности организаций по кредитам банков
|
Год
|
Задолженность по кредитам,
млрд. руб.
|
Абсолютный прирост (цепной),
млрд. руб.
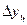
|
Абсолютный прирост (базисный), млрд. руб.
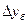
|
Темп роста (цепной)
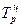
|
Темп роста (базисный)
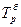
|
Темп прироста (цепной)
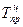
|
Темп прироста (базисный)
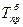
|
|
1
|
960
|
|
|
|
|
|
|
|
2
|
1800
|
840
|
840
|
187,5
|
187,5
|
87,5
|
87,5
|
|
3
|
2400
|
600
|
1440
|
133,333
|
250
|
33,333
|
150
|
|
4
|
3500
|
1100
|
2540
|
145,833
|
364,5833
|
45,833
|
264,583
|
|
5
|
4200
|
700
|
3240
|
120
|
437,5
|
20
|
337,5
|
|
Итого
|
12860
|
3240
|
|
586,667
|
|
|
|
3.
Среднегодовые темпы роста и прироста задолженности:
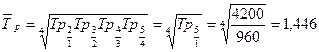 или 144,6%
или 144,6%
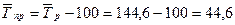 .
.
4. Прогноз
задолженности организаций по кредитам банков при условии, что среднегодовой
темп сохранится на прежнем уровне еще в течение двух лет.
Прогнозирование осуществим методом экстраполяции.
Составим уравнение прямой, представляющее собой трендовую модель: 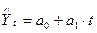 .
.
Расчетные значения представим в виде таблице
17.
Таблица17
Расчетная таблица
|
Год
|
Задолженность по кредитам, млрд. руб.
|
t
|
t2
|
y*t
|
|
1
|
960
|
-2
|
4
|
-1920
|
|
2
|
1800
|
-1
|
1
|
-1800
|
|
3
|
2400
|
0
|
0
|
0
|
|
4
|
3500
|
1
|
1
|
3500
|
|
5
|
4200
|
2
|
4
|
8400
|
|
Итого
|
12860
|
0
|
10
|
8180
|
Следовательно 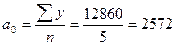 ,
, 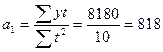 . Таким образом, уравнение трендовой модели, будет иметь вид:
. Таким образом, уравнение трендовой модели, будет иметь вид:
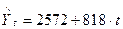 .
.
На основе уравнения 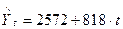 при t =6 и t = 7 можно определить
ожидаемую задолженность в течение следующих двух лет, млрд. руб.:
при t =6 и t = 7 можно определить
ожидаемую задолженность в течение следующих двух лет, млрд. руб.:
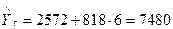 ;
;
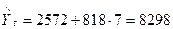 .
.
5.
График динамики задолженности (рис. 3).
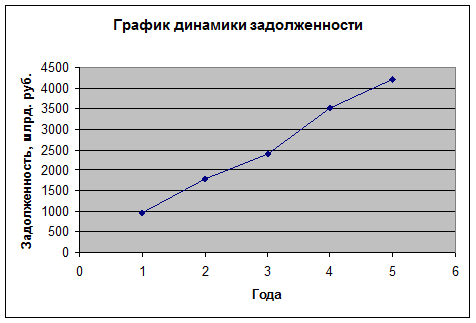
Рис. 3. График
динамики задолженности
Вывод: Исходя
из полученнного графика можно утверждать что задолженностьорганизаций по
кредитам банков имеет положительную тенденцию.
Литература
1.
Гусаров В.М. Статистика: Учеб. Пособие для вузов. – М.: ЮНИТИ-ДАНА, 2003.
2.
Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник / под ред.
И.И. Елисеевой. – М.: Финансы и статистика, 2004.
3.
Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики:
Учебник. – М.: ИФРА-М, 2004.
4.
Общая теория статистики: Статистическая методология в изучении
коммерческой деятельности: Учебник / под ред. О.Э. Башиной, А.А. Спирина. – М.:
Финансы и статистика, 2005.
5.
Практикум по статистике: Учеб. Пособие для вузов / под ред. В.М. Симчеры;
ВЗФЭИ. – М.: Финстатинформ, 1999.
6.
Практикум по теории статистики: Учеб. Пособие / под ред. Р.А. Шмойловой.
– М.: Финансы и статистика, 2004.
7.
Сироткина Т.С., Каманина А.М. Основы теории статистики: Учеб. Пособие для
вузов / ВЗФЭИ. Под ред. проф. В.М. Симчеры. – М.: АО «Финстатинформ», 1996.
8.
Статистика: Учебник / под ред. В.С. Мхитаряна. – М.: Экономистъ, 2005.