Любая сфера человеческой деятельности, в особенности экономика или бизнес, связана с принятием решений в условиях неполноты информации.

Источники неопределенности могут быть самые разнообразные: нестабильность экономической и/или политической ситуации, неопределенность действий партнеров по бизнесу, случайные факторы, т.е. большое число обстоятельств, учесть которые не представляется возможным (например, погодные условия, неопределенность спроса на товары, неабсолютная надежность процессов производства, неточность информации и др.). Экономические решения с учетом перечисленных и множества других неопределенных факторов принимаются в рамках так называемой теории принятия решений – аналитического подхода к выбору наилучшего действия (альтернативы) или последовательности действий. В зависимости от степени определенности возможных исходов или последствий различных действий, с которыми сталкивается лицо, принимающее решение, в теории принятия решений рассматриваются три типа моделей:

– выбор решений в условиях определенности, если относительно каждого действия известно, что оно неизменно приводит к некоторому конкретному исходу;

– выбор решения при риске, если каждое действие приводит к одному из множества возможных частных исходов, причем каждый исход имеет вычисляемую или экспертно оцениваемую вероятность появления;

– выбор решений при неопределенности, когда то или иное действие или несколько действий имеют своим следствием множество частных исходов, но их вероятности совершенно не известны или не имеют смысла.

Методы принятия решений в условиях риска разрабатываются и обосновываются в рамках так называемой теории статистических решений.[1]

Принятие управленческих решений предполагает наличие ситуаций выбора наиболее выгодного варианта поведения из нескольких имеющихся вариантов в условиях неопределённости. Такие задачи могут быть описаны матричными играми особого типа, в которых игрок взаимодействует не со вторым игроком, а с окружающей средой. Объективно окружающая среда не заинтересована в проигрыше игрока. В процессе принятия решения о выборе варианта поведения игрок имеет информацию о том, что окружающая среда может принять одно из нескольких возможных состояний и сталкивается с неопределённостью относительно того конкретного состояния, которое примет окружающая среда в данный момент времени.

Матричная игра, в которой игрок взаимодействует с окружающей средой, не заинтересованной в его проигрыше, и решает задачу определения наиболее выгодного варианта поведения с учётом неопределённости состояния окружающей среды, называется статистической игрой или «игрой с природой». Игрок в этой игре называется лицом, принимающим решение (ЛПР). Создателем теории статистических игр считается А. Вальд. Он показал, что в теории принятия решений статистические игры являются основным подходом, если решение принимается в условиях частичной неопределенности.

Основными отличиями статистической игры от стратегической являются:

– отсутствие стремления к выигрышу у игрока-природы, т. е. отсутствие антагонистического противника;

– возможность второго игрока – статистика провести статистический эксперимент для получения дополнительной информации о стратегиях природы.

Таким образом, теория статистических решений является теорией проведения статистических наблюдений, обработки этих наблюдений и их использования.

В теории статистических решений основные правила могут быть детерминированными и рандомизированными. ЛПР определяет наиболее выгодную стратегию в зависимости от целевой установки, которую он реализует в процессе решения задачи.

Результат решения задачи ЛПР определяет по одному из критериев принятия решения. Для того чтобы прийти к однозначному и по возможности наиболее выгодному варианту решению, необходимо ввести оценочную (целевую) функцию. При этом каждой стратегии ЛПР (ai) приписывается некоторый результат Wi, характеризующий все последствия этого решения. Из массива результатов принятия решений ЛПР выбирает элемент W, который наилучшим образом отражает мотивацию его поведения.

Критерий максимального математического ожидания выигрыша применяется в тех случаях, когда ЛПР известны вероятности состояний окружающей среды. Платёжная матрица дополняется столбцом, каждый элемент которого представляет собой значение математического ожидания выигрыша при выборе соответствующей стратегии ЛПР:

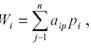
где p_j -  вероятность j-го состояния окружающей среды.

Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой значение математического ожидания выигрыша максимально:

W = max Wi .

Применение критерия максимального математического ожидания выигрыша, таким образом, оправдано, если ситуация, в которой принимается решение, следующая:

1. ЛПР известны вероятности всех состояний окружающей среды.

2. Минимизация риска проигрыша представляется ЛПР менее существенным фактором принятия решения, чем максимизация среднего выигрыша.

Необходимость иметь информацию о вероятностях состояний окружающей среды ограничивает область применения данного критерия.

Критерий недостаточного основания Лапласа используется при наличии неполной информации о вероятностях состояний окружающей среды в задаче принятия решения. Вероятности состояний окружающей среды принимаются равными и по каждой стратегии ЛПР в платёжной матрице определяется, таким образом, среднее значение выигрыша:[2]

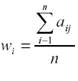
Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой значение среднего выигрыша максимально:

W = max Wi.

Использование данного критерия оправдано в следующей ситуации:

1. ЛПР не имеет информации либо имеет неполную информацию о вероятностях состояний окружающей среды;

2. Вероятности состояний окружающей среды близки по своим

3. Минимизация риска проигрыша представляется ЛПР менее существенным фактором принятия решения, чем максимизация среднего выигрыша.

Правило выбора решения в соответствии с максиминным критерием Вальда (ММ-критерием) можно интерпретировать следующим образом: Платёжная матрица дополняется столбцом, каждый элемент которого представляет собой минимальное значение выигрыша в соответствующей стратегии ЛПР:

Wi = minj aij.

Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой минимальное значение выигрыша максимально:

W = max Wi.

Выбранная таким образом стратегия полностью исключает риск. Это означает, что принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Это свойство позволяет считать ММ-критерий одним из фундаментальных.

Применение ММ-критерия оправдано, если ситуация, в которой принимается решение следующая.

1. О возможности появления состояний окружающей среды ничего не известно.

2. Решение реализуется только один раз.

3. Необходимо исключить какой бы то ни было риск.

В случае использования критерия минимаксного риска Сэвиджа величина (amax j – aij ), где amax j – максимальный элемент j-го столбца может быть интерпретирован как дополнительный выигрыш, получаемый в условиях состояния окружающей среды Sj при выборе ЛПР наиболее выгодной стратегии, по сравнению с выигрышем, получаемым ЛПР при выборе в тех же условиях любой другой стратегии. Эта же разность может быть интерпретирована как величина возможного проигрыша при выборе ЛПР I-й стратегии по сравнению с наиболее выгодной стратегией. На основе данной интерпретации разности выигрышей производится определение наиболее выгодной стратегии по критерию минимаксного риска.

Для определения оптимальной стратегии по данному критерию на основе платёжной матрицы рассчитывается матрица рисков, каждый коэффициент которой (rij) определяется по формуле:[3]

rij = amax j – aij

Матрица рисков дополняется столбцом, содержащим максимальные значения коэффициентов rij по каждой из стратегий ЛПР:

Ri = maxj rij.

Оптимальной по данному критерию считается та стратегия, в которой значение Ri минимально:

W = min Ri.

Ситуация, в которой оправдано применение критерия Сэвиджа, аналогична ситуации ММ-критерия, однако наиболее существенным в данном случае является учёт степени воздействия фактора риска на величину выигрыша.

В практике принятия решений ЛПР руководствуется не только критериями, связанными с крайним пессимизмом или учётом максимального риска. Стараясь занять наиболее уравновешенную позицию, ЛПР может ввести оценочный коэффициент(критерий пессимизма-оптимизма Гурвица), называемый коэффициентом пессимизма, который находится в интервале [0, 1] и отражает ситуацию, промежуточную между точкой зрения крайнего оптимизма и крайнего пессимизма. Данный коэффициент определяется на основе статистических исследований результатов принятия решений или личного опыта принятия решений в схожих ситуациях.[4]

Платёжная матрица дополняется столбцом, коэффициенты которого рассчитываются по формуле:

Wi = C·minj aij + (1-C) ·maxj aij, (6)

где C – коэффициент пессимизма.

Оптимальной по данному критерию считается стратегия, в которой значение Wi максимально:

W = max Wi.

При С=1 критерий Гурвица превращается в ММ-критерий. При С = 0 он превращается в критерий «азартного игрока», делающего ставку на то, что «выпадет» наилучший случай.

Критерий Гурвица применяется в ситуации, когда:

1. Информация о состояниях окружающей среды отсутствует или недостоверна.

2. Необходимо считаться с появлением каждого состояния окружающей среды.

3. Реализуется только малое количество решений.

4. Допускается некоторый риск.

Критерий Ходжа-Лемана опирается одновременно на ММ-критерий и критерий максимального математического ожидания выигрыша. При определении оптимальной стратегии по этому критерию вводится параметр достоверности информации о распределении вероятностей состояний окружающей среды, значение которого находится в интервале [0, 1]. Если степень достоверности велика, то доминирует критерий максимального математического ожидания выигрыша, в противном случае – ММ-критерий.[5]

Платёжная матрица дополняется столбцом, коэффициенты которого определяются по формуле:

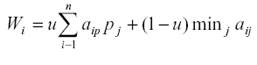
где u – параметр достоверности информации о вероятностях состояний окружающей среды.

Оптимальной по данному критерию считается та стратегия, в которой значение Wi максимально:

W = max Wi.

Данный критерий применим в следующем случае:

1. Имеется информация о вероятностях состояний окружающей среды, однако эта информация получена на основе относительно небольшого числа наблюдений и может измениться.

2. Принятое решение теоретически допускает бесконечно много реализаций.

3. При малом числе реализации допускается некоторый риск.

Задача 1. Х=2

Для Вашей компании существуют 4 возможных направления инвестирования капитала:

1.     Облигации государственного займа, по которым гарантировано 7% дохода. Эти облигации выпускаются на 1 году, т.е через годы все они выкупаются государством.

2.     Облигации газовой компании с фиксированным доходом и сроком займа на 10 лет. Однако, Ваша компания продает облигации в конце 1-го года, т.е. процент будет известен в конце года (см. таблицу).

3.     Проект А, предполагающий нулевые поступления в течение года и выплаты в конце года, которые будут зависеть от состояния экономики.

4.     Проект В, аналогичный проекту А, но с другим распределением выплат.

Требуется оценить ожидаемый доход и риск для всех четырех вариантов и выбрать один из них. Информация о предполагаемых доходах содержится в таблице.

Таблица 1. Норма дохода, %

При выборе решения в качестве критериев риска используется показатель:

R = H_ij ∙ p

где р – вероятность наступления рискового события.

Предпочтение отдается решению, имеющему наименьший средневзвешенный показатель риска, определяемый как сумма произведений вероятностей различных вариантов обстановки на соответствующее им значение потерь:

R_i =∑_j=1H_ij ∙ p_j,     (i=1,m)

Потери (Н_ij) рассчитываются как разность между ожидаемым результатом действия при наличии точных данных обстановки и результатом, который может быть достигнут, если данные определены:

Н_{ij (PiOj)} = max_j a_ij – a_ij

Определим для нашей задачи max_j a_ij. (табл. 2).

Таблица 2 – Расчет max_j a_ij

Теперь определим величины потерь для каждого варианта инвестирования капитала и для каждого состояния экономики (табл. 3).

Рассчитаем показатель риска для каждого варианта решения, воспользовавшись формулой: R_i =∑_j=1H_ij ∙ p_j,     (i=1,m), табл. 5.

Таблица 5 - Расчет показателя риска для каждого варианта решения

Общая величина риска при различных вариантах инвестирования приведена в табл. 6.

Таблица 6 - Общая величина риска при различных вариантах инвестирования

Таким образом, наименее рискованным является приобрести облигации газовой компании. Здесь подразумевается риск упущенной выгоды[6] (потери).

Выбор того или иного решения зависит не только от целевых установок и ограничений, но и от склонности к риску лиц, принимающих данное решение.

Одним из классических критериев, учитывающих также и этот параметр, является критерий обобщенного максимина (пессимизма-оптимизма) Гурвица. Данный критерий, как правило, используется, если требуется остановиться между стратегией (линией поведения) в расчете на худшее и линией поведения в расчете на лучшее.

В этом случае предпочтение отдается варианту решений, для которого окажется максимальный показатель G_i, определенный по формуле:

G_i = k ∙(min_j a_ij) + (1-k)∙ (max_j a_ij)

где k – коэффициент, рассматриваемый как показатель оптимизма (0≤k≤1), при этом k=0 – линия поведения в расчете на лучшее, при k=1 – в расчете на худшее; а_ij – выигрыш, соответствующий i-му решению при j-м варианте обстановки. При k=1 критерий Гурвица ориентирован на осторожное поведение. При k=0 – ориентация на предельный риск, т.к. большой выигрыш, как правило, сопряжен с большим риском. Значения k между 0 и 1 являются промежуточными между риском и осторожностью и выбираются в зависимости от обстановки и склонности к риску лица, принимающего решения.

Определим критерии Гурвица для различных вариантов решений и значений коэффициента k, для этого воспользовавшись вспомогательной таблицей, в которой мы определим максимальные и минимальные значения a_ij. (табл. 7).

Таблица 7 – Расчет критериев Гурвица

Определение оптимального решения с учетом критерия Гурвица приведено в табл. 8.

Таблица 8 - Определение оптимального решения с учетом критерия Гурвица

Из данных таблицы видно, что в условиях неопределенности лицо, ориентированное на любое поведение, кроме риска, выберет реализацию оптимального для него решения Р₂, и только лицо, ориентированное на предельный и близкий к предельному риск, предпочтет реализацию оптимального решения Р₄. Выбором является решение P2.

Задача 2. X=2

Выпускник НГАЭиУ рассматривает два варианта трудоустройства:

А) создать малое предприятие и получать доход 3 тыс. у.е. в месяц с вероятностью 60 % или 2 тыс. у.е. в месяц с вероятностью 40 %;

Б) устроиться на работу с фиксированным доходом 2 тыс. у.е. в месяц.

Полезность в зависимости от дохода для выпускника представлена в таблице 9.

Таблица 9 - Полезность в зависимости от дохода для выпускника

Какую работу выберет выпускник, максимизирующий полезность и чему равна премия за риск?

Исходя из условия максимизации полезности, выпускник должен выбрать работу с полезностью 21 или 29 у.е. Такую полезность он получит при доходе 2,9и 3,0  тыс. рублей, соответственно.

Так как создание малого предприятия может обеспечить 3,0 тыс. руб. в месяц, при этом полезность равна 29., значит выпускник предпочтет данную работу (из условия максимизации полезности).

Премия за риск составляет 1 тыс. рублей (см. табл. 10).

Таблиц 10 - Премия за риск

Задача 3. Х = 2

Добавочные вложения в расширение производства в размере 50 тыс. у.е. могут увеличить прибыль от реализации продукции со 100 тыс. у.е. до 200 тыс. у.е. при условии, что спрос на нее возрастает.

Эти вложения окажутся напрасными, если спрос не увеличится. Вероятность увеличения спроса по мнению экспертов равна 0,7.

Можно заказать прогноз спроса специализированной фирме, занимающейся изучением рыночной конъюнктуры за 2 тыс. у.е. Как положительный, так и отрицательный прогноз сбываются с вероятностью 0,9. Необходимо принять решение о целесообразности дополнительных вложений и целесообразности заказа прогноза с целью снижения риска из-за неопределенности спроса на продукцию (построить «дерево решений» с использованием формулы Байеса).

В данном случае предположение о росте спроса и об отсутствии роста спроса можно обозначить как гипотезы Н₁ и Н₂. По условию задачи известны Р (Н₁) и Р(Н₂).

Получение положительного или отрицательного прогноза от специализированной фирмы обозначим как А и Ậ.

По условию задачи знаем вероятность того, что положительный или отрицательный прогноз сбудется: Р(А/Н₁) = Р(Ậ./Н₂) = 0,9. Отсюда вероятность того, что прогнозы будут ошибочными: Р(А/Н₂) =  Р(Ậ./Н₁) = 0,1. Для построения «дерева решений» необходимо:

1. Определить вероятность, с которой может быть получен положительный прогноз (событие А) от специализированной фирмы, занимающейся изучением рыночной конъюнктуры. Если она окажется очень маленькой, целесообразно отказаться от заказа прогноза. Для этой цели нужно использовать формулу полной вероятности:

Р(А) = ∑Р(А/Н_i) ·Р(Н_i) = 0,9*0,7+0,1*0,3 = 0,66

2. Определить, с какой вероятностью можно будет ожидать рост спроса, если будет получен положительный прогноз. Используем формулу Байеса. Зная Р(Н₁/А), найдем вероятность падения спроса при получении положительного прогноза: Р(Н₂/А) = 1 – Р(Н₁/А).

3. Вычислить, с какой вероятностью можно будет ожидать рост спроса, если будет получен отрицательный прогноз. Такое может произойти, т.к. фирма, специализирующаяся на прогнозах, не гарантирует абсолютной точности: 10% ее прогнозов не сбываются. Используя формулу Байеса и найдем Р(Н₁/ Ậ).

Р(Н₁ /А)  = Р(А/Н₁) ·Р(Н₁) / Р(А),

где Р(Н₁ /А) – уточненная апостериорная вероятность гипотезы Н₁

Р(Н₁) - ее первоначальная, т.е. априорная вероятность

Р(А) – полная вероятность наступления события А.

Вероятность получения отрицательного прогноза: Р(Ậ) = 1-Р(А) = 1-0,66 = 0,34

Отсюда вероятность падения спроса при получении отрицательного прогноза составит: Р(Н₂/ Ậ)= 1 – Р(Н₁/ Ậ).

Р(Н₁ /А)  = Р(А/Н₁) ·Р(Н₁) / Р(А) = 0,7·0,9/0,66 = 0,95

Вероятность падения спроса при получении положительного прогноза Р(Н₂/А):

1 – 0,95 = 0,05

Найдем, с какой вероятностью можно будет ожидать рост спроса, если будет получен отрицательный прогноз:

Р(Н₁ /Ậ)  = Р(Ậ/Н₁) ·Р(Н₁) / Р(Ậ) = 0,3·0,9/0,34 = 0,79

Вероятность падения спроса Р (Н₂/Ậ) при получении отрицательного прогноза составит:

Р (Н₂/Ậ) = 1 - Р(Н₁ /Ậ)  = 0,21

Результаты расчетов используем при составлении «дерева решений».

D_i – доход предприятия при данном направлении развития событий

Е(D_i)- ожидаемый доход с учетом вероятностей.

Критерием выбора оптимальной альтернативы является максимальное значение дохода (ожидаемого дохода).

Таким образом, как видно из рис. 1, целесообразно инвестировать в расширение производства, а также целесообразно заказать прогноз спроса специализированной фирме.

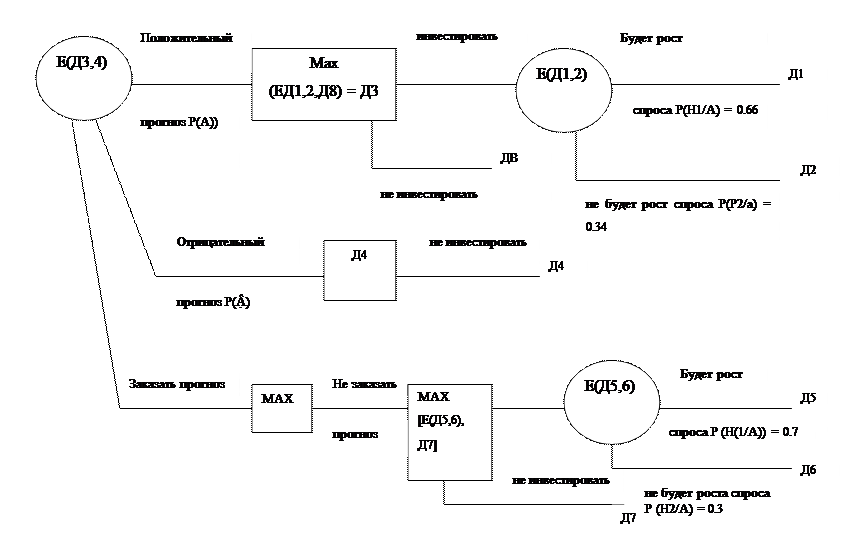
Рисунок 1 – Дерево решений

Задача 4. X=2

В первых графах таблицы приведены статистические данные о финансовых инструментах А, Б и В. Проанализировать риск[7] этих инструментов (оценить стандартное отклонение и коэффициент вариации), а также возможных портфелей, если предприниматель может выбрать одну из двух стратегий:

а) выбрать один из финансовых инструментов;

б) составить портфель, в котором 50% будет составлять один из активов и 50% - другой.

Таблица 11 - Годовые % возможных инвестиций

Коэффициент вариации (ν) рассчитывается по формуле:

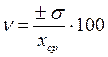
Стандартное отклонение (σ):

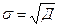
Дисперсия (Д):

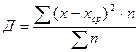
Таблица 12 – Расчет для инструмента А

Таблица 13 - Расчет для инструмента Б

Таблица 14 - Расчет для инструмента В

Таблица 15 - Расчет для инструмента АБ

Таблица 16 - Расчет для инструмента БВ

Таблица 17 - Расчет для инструмента АВ

Сгруппируем полученные данные по коэффициенту вариации, т.е. по степени риска (табл. 18).

Таблица 18 – Группировка полученных данных по степени риска

Если предприниматель должен выбрать один из финансовых инструментов А, Б, или В (стратегия а), то наименее рискованным для него будет инструмент А (коэффициент вариации 3,7%).

Если предприниматель может составить портфель из этих инструментов, то наименее рискованным является портфель АВ, включающий 50% инструмента А и 50% инструмента В.

Задача 5. X=2

В портфеле предприятия «Сибин» находятся два вида акций с разными среднегодовыми нормами доходности – акции «А» и акции «Б» с соответствующими характеристиками абсолютного размера риска в виде среднеквадратических отклонений σ (А) и σ (Б). Коэффициент корреляции текущих норм доходности акций «А» и «Б» равен: –1.

Таблица 19 – Исходные данные

Найти пропорцию распределения денежных средств, инвестируемых в акции, соответствующие минимуму риска (нулевой дисперсии).

Известно, что коэффициент корреляции равен[8] –1. Данный коэффициент рассчитывается по формуле:

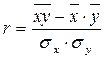,                                                                                    (1)

где х и y – зависимые величины. В нашем случае это нормы доходности акций А и Б, т.е.:

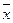 = 15

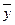 = 20,5

Подставим значения этих величин в формулу коэффициента корелляции:

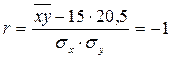
Выразим :

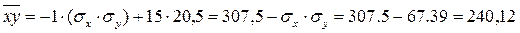
Значит средняя величина произведений норм доходности акций А и Б равна 240,12.

При распределении денежных средств, соответствующим минимуму риска, дисперсия стремится к нулю.

Выразим из формулы (1) произведение σ_А σ_Б и приравняем к нулю.

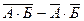= 0

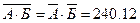
Значит распределение средств должно быть таким, чтобы произведение средних норм доходности акций было равно 240,12.

Список литературы

1. Романов В.С. Понятие рисков и их классификация как основной элемент теории рисков // Инвестиции в России. — 2005г. —  № 12, с. 41—43

2. Романов В.С., Бутуханов А. В. Рискообразующие факторы: характеристика и влияние на риски // Управление риском. —  2001 г. № 3, с.10—12.

3. Романов В. С. Риск-менеджмент как условие развития  предприятия. Теория и практика реструктуризации предприятий: Сборник материалов Всероссийской  научно-практической  конференции. Пенза, 2001 г. — с.144—146.

4. Романов В. С. Управление рисками: этапы и методы // Факты и проблемы практики менеджмента: Материалы научно-практической конференции 30 октября 2001 г. —  Киров:  Изд-во  Вятского   ГЛУ, 2001 г. — с. 71—77.

5. Станиславчик Е. Н. Риск-менеджмент на предприятии. Теория и практика. М.: «Ось-89», 2002. – 80 с..

[1] Романов В.С. Понятие рисков и их классификация как основной элемент теории рисков // Инвестиции в России. — 2005г. —  № 12, с. 41—43

[2] Станиславчик Е. Н. Риск-менеджмент на предприятии. Теория и практика. М.: «Ось-89», 2002. – 80 с..

[3] Станиславчик Е. Н. Риск-менеджмент на предприятии. Теория и практика. М.: «Ось-89», 2002. – 80 с..

[4] Станиславчик Е. Н. Риск-менеджмент на предприятии. Теория и практика. М.: «Ось-89», 2002. – 80 с..

[5] Романов В. С. Риск-менеджмент как условие развития  предприятия. Теория и практика реструктуризации предприятий: Сборник материалов Всероссийской  научно-практической  конференции. Пенза, 2001 г. — с.144—146.

[6] Романов В.С. Понятие рисков и их классификация как основной элемент теории рисков // Инвестиции в России. — 2000г. —  № 12, с. 41—43

[7] Романов В. С. Управление рисками: этапы и методы // Факты и проблемы практики менеджмента: Материалы научно-практической конференции 30 октября 2001 г. —  Киров:  Изд-во  Вятского   ГЛУ, 2001 г. — с. 71—77.

[8] Романов В. С. Риск-менеджмент как условие развития  предприятия. Теория и практика реструктуризации предприятий: Сборник материалов Всероссийской  научно-практической  конференции. Пенза, 2001 г. — с.144—146.