Всероссийский заочный
финансово – экономический институт.
Кафедра Высшей
математики и информатики
Контрольная работа № 1
Дисциплина: Математический анализ и линейная
алгебра
Тема: Вариант №10
Исполнитель:
Специальность:
Группа:
№ зачетной книжки:
Руководитель:
Барнаул 2007 г.
1.
Вычислить
определитель матрицы С = А2 + 3А – Е разложением по второй строке,
где А = 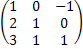 Е – единичная матрица. Являются ли
столбцы матрицы С линейно независимыми?
Е – единичная матрица. Являются ли
столбцы матрицы С линейно независимыми?
Решение:
Вычислим
матрицу С.
1)
А2
= А*А
Произведением
матриц А*В называется такая матрица С,
каждый элемент
mxk kxn mxn
которой
Cij равен сумме произведений элементов i – й строки матрицы А на соответствующие элементы j – го столбца матрицы В.
k
Сij = ∑ ais
* bsj, i = 1,2,…,m, j = 1,2,…,n.
s = 1
A2 = 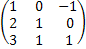 *
* 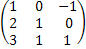 =
= 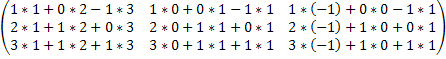 =
= 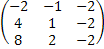 .
.
Произведением матрицы А на число
λ называется матрица В = λ*А, элементы которой bij = λaij
для
i = 1,2,…,m, j = 1,2,…,n.
3*A = 3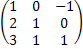 =
= 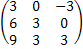 .
.
E
= 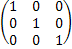 – единичная матрица.
– единичная матрица.
Суммой двух матриц А и В одинакового
размера называется матрица С = А+В, элементы которой
Сij = aij+bij для i = 1,2,…,m, j = 1,2,…,n.
С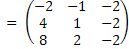 +
+ 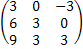 –
– 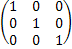 =
= 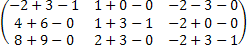 =
=
=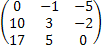 .
.
Теорема Лапласа: Определитель квадратной
матрицы равен сумме произведений элементов любой строки (столбца) на их
алгебраические дополнения.
Алгебраическим дополнением Aij элемента aij
матрицы А называется
Aij = (-1)i+j * Mij.
Mij – минор
элемента аij – это
определитель матрицы, полученной из матрицы А вычеркиванием i-й строки и j-го
столбца.
Вычислим определитель матрицы С разложением
по второй строке матрицы.
∆с =| 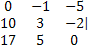 = 10 * (-1)2+1
*
= 10 * (-1)2+1
* 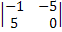 + 3 * (-1)2+2
*
+ 3 * (-1)2+2
* 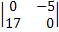 – 2 *(-1)2+3
*
– 2 *(-1)2+3
* 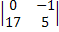 =
=
-10* (-1+25) + 3*(0+85) + 2*(0+17) = -240 + 255 + 34 = 39.
Выясним
являются ли столбцы матрицы С = 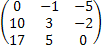 линейно
независимыми.
линейно
независимыми.
Рангом
матрицы А называется наивысший порядок отличимых от нуля миноров этой матрицы.
Для квадратной матрицы n – го порядка r(A) = n тогда и только
тогда, когда матрица А – невырожденная.
∆с
= 39 ≠ 0. Значит, С – невырожденная матрица. Её ран равен 3.
И по
теореме: ранг матрицы равен максимальному числу её линейно независимых строк
или столбцов, через которые линейно выражаются все остальные её строки
(столбцы) r(C) = 3. Значит и
число линейно независимых столбцов равно 3. Значит, все столбцы матрицы С –
линейно независимыми.
Ответ: Определитель
матрицы С ∆с = 39. Все столбцы С линейно независимы.
2.
Найти предел.
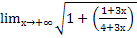 1-2х
1-2х
Решение:
у
= 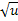 - непрерывная
функция. Под знаком непрерывной функции можно переходить к пределу.
- непрерывная
функция. Под знаком непрерывной функции можно переходить к пределу.
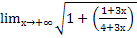 1-2х =
1-2х = 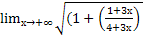 1-2х) Если
предел
1-2х) Если
предел 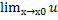 = a;
= a; 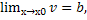 то
то
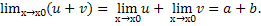
Найдем 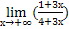 1-2х = [1∞]
=
1-2х = [1∞]
= 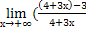 )1-2х =
)1-2х = 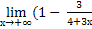 )1-2х =
)1-2х = 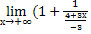 )1-2х =
)1-2х =
= [обозначим 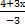 =t; 4+3x=-3t; 3x = -3t-4; x =
=t; 4+3x=-3t; 3x = -3t-4; x = 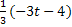 ] =
] = 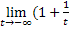 )1-2/3 (-3t-4) =
)1-2/3 (-3t-4) = 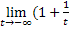 )2t+11/3 =
)2t+11/3 =
при х→+∞
t→-∞
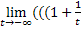 )t)2
* (
)t)2
* (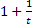 )11/3) = [по второму замечательному пределу
)11/3) = [по второму замечательному пределу 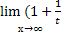 )t
= e]
= e2*1=e2.
)t
= e]
= e2*1=e2.
Тогда 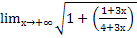 1-2х =
1-2х = 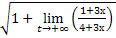 1-2х =
1-2х = 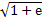 2
2
Ответ: 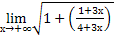 1-2х ≈
2,896
1-2х ≈
2,896
3.
Найти производную функции у = 3*2-хℓn3(2+2х);
Решение:
Применяемые
формулы:
|
(u · v)' = u' · v + u · v'; (k ·
u)' = k · u', k – const; (uα)' = α · uα-1
· u'; (k)' = 0, k – const;
(2x)' = 2x
ℓn2; 2u = (2u · ℓn2) · u'; (ℓn u)' = 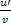 . .
|
y' = (3·2-x(-1)·ℓn2)
ℓn3 (2+2x) + 3·2-x · 3ℓn2
(2+2x) · 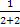 x · (0+2xℓn2) =
x · (0+2xℓn2) =
= -3·2-xℓn2·ℓn3(2+2x)+9·ℓn2(2+2x)
· 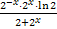 = 3·ℓn2(2+2x)·ℓn2(-2-x·ℓn(2+2x)
+
= 3·ℓn2(2+2x)·ℓn2(-2-x·ℓn(2+2x)
+  );
);
Ответ: у' = 3·ℓn2(2+2x)·ℓn2(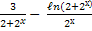 ).
).
4.
Площадь,
занимаемая печатным текстом составляет на странице книги 432 см2.
Ширина полей вверху и внизу страницы составляет 2 см, а ширина боковых полей
по 1,5 см.
Каковы должны быть ширина и высота страницы, чтобы количество израсходованной
бумаги было наименьшим.
Решение:
Обозначим х – ширина страницы (см); у – высота страницы
(см).
Площадь страницы, S = x · y должна быть минимальной.

Ширина текста х-3 (см),
Высота текста у – 4 (см).
у
х
Площадь
текста: 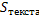 = (х-3) · (у-4); 432
= (х-3) · (у-4). Отсюда: у – 4 =
= (х-3) · (у-4); 432
= (х-3) · (у-4). Отсюда: у – 4 = 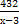 ; у = 4 +
; у = 4 + 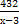 ; у =
; у = 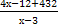 ; у =
; у = 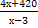 . Тогда S = х ·
. Тогда S = х · 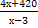 ; или S =
; или S = 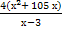 ; По условию задачи х > 3.
; По условию задачи х > 3.
Исследуем функцию S = 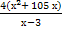 ; х є (3,+∞) на наибольшее и наименьшее значения.
; х є (3,+∞) на наибольшее и наименьшее значения.
1.
Находим критические точки
S' = 4 · 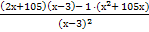 =
= 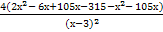 =
= 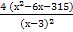 .
.
2.
Находим критические точки
S' = 0 => 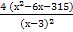 = 0 => х2
– 6х – 315 = 0; х1,2 = 3 ±
= 0 => х2
– 6х – 315 = 0; х1,2 = 3 ±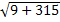 = 3 ±
= 3 ±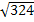 = 3 ± 18. х1 = -15¢ (3, +∞)
(не рассматриваем) х2 = 21
є (3, +∞).
= 3 ± 18. х1 = -15¢ (3, +∞)
(не рассматриваем) х2 = 21
є (3, +∞).
3.
Находим значение S (21);
S (21) = 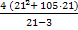 = 588 (см2)
= 588 (см2)
4.
Исследуем концы промежутка.
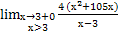 = [
= [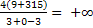 ] = +∞
] = +∞
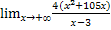 = [
= [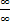 , правило Лопиталя] =
, правило Лопиталя] = 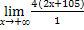 = +∞
= +∞
5.
Вывод: наименьшее значение, равно
588 функция достигает при х=21. Ширина
страницы 21 см.
Высота страницы: у = 4+ 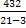 = 4+24 = 28 (см)
= 4+24 = 28 (см)
Ответ: наименьшее количество бумаги будет израсходовано, если
ширина страницы 21 см,
высота страницы 28 см.
5. Составить уравнения касательных к графику
функции у = х3 – х, перпендикулярных прямой, пересекающейся с осью
Ох в точке х=6 и с осью Оу в точке у=3. Сделать чертёж
Решение:
Исходя из геометрического смысла
производной, уравнение касательной к графику функции, проведенной в точке (х0,у0),
имеет вид:
у
– у0 = f ' (x0)(x-x0). (1)
Найдем f ' (х) = (х3 – х)' = 3х2
– 1; касательная перпендикулярна прямой, отсекающей на оси Ох отрезок, равный 3. Уравнение прямой в
отрезках на осях имеет вид:  +
+  = 1.
= 1.
Тогда  +
+  = 1 или
х+2у = 6 Или: у = -
= 1 или
х+2у = 6 Или: у = -  х + 3. Угловой коэффициент этой прямой
х + 3. Угловой коэффициент этой прямой 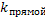 = -
= -  ; Условие перпендикулярности
прямых k1 · k2 = -1. Угловой
коэффициент касательной
; Условие перпендикулярности
прямых k1 · k2 = -1. Угловой
коэффициент касательной 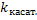 = 2.
= 2.
М1 (+1;0); у – 0 = 2 (х-1); 2х – у – 2 = 0.
М2 (-1;0); у – 0 = 2 (х-(-1)); у – 0 = 2х + 2; 2х – у + 2 = 0;
Выполним построения.
2х – у – 2 = 0 2х – у + 2 = 0 у = х3 – х, - кубическая
парабола
|
х
|
0
|
1
|
-1
|
≈ - 0,6
|
≈ 0,6
|
|
у
|
0
|
0
|
0
|
≈ 0,4
|
≈ - 0,4
|
у
' = 3х2 – 1; у ' = 0 при х = - 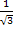 , х =
, х = 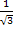 ≈ 0,6.
≈ 0,6.


 +
- + знак у '
+
- + знак у '


 -
-
 х
х
max
 min y
min y
 2x-y+2=0
2x-y+2=0
3 2x-y-2=0
M2 0 M1 6 x
x
+ 2y = 6
y=x3-x
Ответ:
Касательные к кривой у = х2-х,
перпендикулярные прямой х+2у = 6
1. 2х
– у + 2 = 0;
2. 2х
– у – 2 = 0.
6. Исследовать
функцию у = 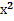 ·
·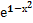 и схематично построить её график.
и схематично построить её график.
Решение:
1. Область
определения:
х є
(-∞,+∞), т.к. х2 и 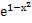 определены при любых значениях х.
определены при любых значениях х.
2. Непрерывность.
у1
= х2 непрерывна как квадратичная функция (х є (-∞,+∞))
у2
= 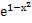 непрерывна как сложная показательная функция:
у2 = е u
,
u
= 1-x2
при х є (-∞,+∞).
непрерывна как сложная показательная функция:
у2 = е u
,
u
= 1-x2
при х є (-∞,+∞).
Произведение
двух непрерывных функций есть функция непрерывная.
Значит,
у = 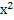 ·
·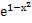 непрерывна при
всех х є (-∞,+∞).
непрерывна при
всех х є (-∞,+∞).
3. Четность,
нечетность
f
(-х) = (-х)2 · 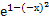 =
= 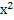 ·
·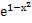 = f(х).
= f(х).
Данная
функция – четная. Её график симметричен относительно оси Оу.
4. Асимптоты.
Вертикальных
асимптот нет, т.к. нет точек разрыва II рода. Невертикальные асимптоты имеют
вид
у
= k·x +b, где k = 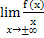 ; b
=
; b
= 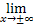 ( f (x) – kx).
( f (x) – kx).
Найдем
k
= 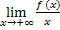 =
= 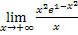 =
= 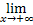 x
x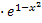 = [∞·0 - неопределенность] =
= [∞·0 - неопределенность] = 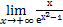 = [
= [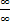 ,правило Лопиталя] =
,правило Лопиталя] = 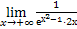 = [
= [ ].
].
b = 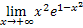 = [∞·0] =
= [∞·0] = 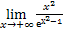 = [
= [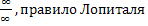 ]
=
]
=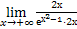 = =
= =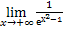 = [
= [ ]
= 0
]
= 0
y = 0 – правая невертикальная
асимптота. Т.к. график четной функции симметричен относительно оси Оу, то у = 0
является и левой невертикальной асимптотой. Т.Е. у = 0 – асимптота.
5. Монотонность.
Экстремум.
Находим
у ';
у
' = 2х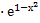 +
+ 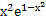 · (-2х); у ' = 2х
· (-2х); у ' = 2х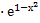 · (1 -
· (1 - 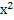 ); у ' = 0 =>
x
= 0, x
= 1, x
= -1 – это критические точки, найденные по необходимому условию экстремума ( В
точках экстремума производная дифференцируемой функции равно нулю).
); у ' = 0 =>
x
= 0, x
= 1, x
= -1 – это критические точки, найденные по необходимому условию экстремума ( В
точках экстремума производная дифференцируемой функции равно нулю).


 +
- + - знак у'
+
- + - знак у'



 х Критические точки разбивают область
определения на
х Критические точки разбивают область
определения на
 -1
0 1
промежутки: (-∞,-1), (-1,0), (0,1),
(1,+∞).
-1
0 1
промежутки: (-∞,-1), (-1,0), (0,1),
(1,+∞).
Определяем знак у' на каждом промежутке. х
є (-∞,-1);
Возьмем х = -2; у'(-2) = - 4 · 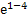 · (1-4) = 12 е-3 >0; -2 є
(-∞, -1) значит при х є (-∞, -1), у' > 0. По достаточному
условию возрастания функция возрастает на этом промежутке.
· (1-4) = 12 е-3 >0; -2 є
(-∞, -1) значит при х є (-∞, -1), у' > 0. По достаточному
условию возрастания функция возрастает на этом промежутке.
х
є (-1,0); х = -  є (-1,0);
у' (-
є (-1,0);
у' (-  ) = 2· (-
) = 2· (-  ) ·
) · 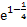 (1 -
(1 -  ) < 0
) < 0
Значит, при х є (-1,0) функция убывает (по
достаточному условию убывания дифференцируемой функции)
х є (0;1);
 є (0;1);
у' (
є (0;1);
у' ( ) = 2 ·
) = 2 · 
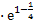 · (1-
· (1-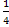 ) > 0 При х є
(0;1); у ' > 0 => функция
возрастает
) > 0 При х є
(0;1); у ' > 0 => функция
возрастает
х
є (1; +∞); 2 є (1; +∞); у '(2) =
2·2·е1-4·(1-4) < 0
=> функция убывает.
При переходе через точку х = -1 производная
меняет знак с «+» на «-». По первому достаточному признаку экстремума в этой
точке максимум уmax
= у (-1) = (-1)2 · е1-1 = 1
М1 (-1;1) – точка максимума. При
переходе через точку х = 0 производная меняет знак с «-» на «+». По первому достаточному условию экстремума в
этой точке минимум. уmin
= у (0) = 0·е1-0 = 0
М2 (0;0) – точка минимума. При
переходе через точку х = 1 производная меняет знак с «+» на «-». В этой точке
максимум. уmax
= у (1) = 1· е1-1 = 1
М3 (1;1) – точка максимума.
Построим схематично график этой
функции.
 у
у
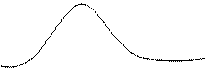
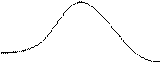
 1
1
 х
х
-1 0
1
Литература:
Высшая математика для
экономистов: Учебник для вузов /Под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ,
2002г.