КУРСОВАЯ РАБОТА

по дисциплине «статистика»

на тему:

«Статистические методы изучения взаимосвязей производственных показателей фирмы

 (на примере производительности труда и заработной платы)»

Вариант № 11

Уфа, 2006 г.

Оглавление:

Введение……………………………………………………………….3

I. Теоретическая часть………………………………………….…..…4

Виды взаимосвязей……………………………………………......…..4

Методы изучения взаимосвязей…………………………………....…5

1.      Метод аналитических группировок…………………………..….6

2.      Метод параллельных рядов…………………………………….…6

3.      Балансовый метод…………………………………………………8

4.      Графический метод…………………………………………......…8

4.1. Классификация видов графиков…………………………...…....11

5.      Корреляционно-регрессионный анализ……………………..….12

6.      Индексный метод………………………………………………...18

II. Практическая часть……………………………………………..…20

III. Аналитическая часть……………………………………………..35

Заключение……………………………………………………………46

Список литературы……………………………………………….…..47

Введение.

Все процессы, протекающие внутри любой фирмы взаимосвязаны между собой. Cтатистическое изучение этой взаимосвязи имеет особо важное значение в связи с тем, что оно позволяет выявить закономерности развития и осуществить прогнозирование этих процессов.

Каждый процесс и явление можно рассматривать с двух сторон. С первой стороны они испытывают влияние других явлений и процессов и выступают как результат этого влияния. С другой стороны каждое явление в свою очередь выступает как фактор, оказывающий влияние на другие явления и процессы. Поэтому признаки, которые испытывают влияние, называются результативными; признаки, которые оказывают влияние - факторные.

Результативные признаки обозначаются через Y, факторные через X. Поэтому в общем виде взаимосвязь между результатом и факторами можно записать формулой:

                               f_y =(x₁ ,x₂ …)

следовательно, Y является функцией от всех X.

Исследуя явления в самых различных областях, статистика сталкивается с зависимостями, как между количественными, так и между качественными показателями, признаками. При этом задача статистики – обнаружить (выявить) такие зависимости и дать их количественную характеристику.

Статистика разработала множество методов изучения связей, выбор которых зависит от целей исследования и от поставленных задач. В своей курсовой работе я попытаюсь осветить основные методы изучения взаимосвязей производственных показателей фирмы, показать классификацию взаимосвязей и дать им оценку.

В аналитической части, на примере 30 предприятий  постараюсь показать конкретное использование методов, описываемых в теоретической части работы. В процессе работы над курсовой используются программы MS Office (Excel и Word)

I. Теоретическая часть.

Виды взаимосвязи

Статистика различает следующие виды взаимосвязи:

1.     Функциональная - одному значению фактора соответствует одно или несколько четко определенных значений результата. Например, S=Vt.

2.     Статистическая - каждому значению фактора соответствует неопределенное множество значений результата.

По направлению различают связь:

1.     Прямая - движение фактора и результата направлены в одну сторону, то есть с увеличением факторного признака увеличивается и результативный, и, наоборот, с уменьшением факторного признака уменьшается и результативный признак.  

2.     Обратная – движение фактора и результата разнонаправлены.

Например, чем выше квалификация рабочего (разряд), тем выше уровень производительности труда – прямая связь. А чем выше производительность труда, тем ниже себестоимость единицы продукции – обратная связь.

По аналитическому выражению:

1.     Прямолинейная – с возрастанием значения факторного признака происходит непрерывное возрастание (или убывание) значений результативного признака. Математически такая связь представляется уравнением прямой, у = а + bx, а графически – прямой линией. Отсюда ее более короткое название – линейная связь.

2.     Криволинейная – с возрастанием значения факторного признака возрастание (или убывание) результативного признака происходит неравномерно, или же направление его изменения меняется на обратное. Геометрически такие связи представляются кривыми линиями, например, уравнением параболы, гиперболы и других кривых  y = x² + bx + c.

По количеству факторов, действующих на результативный признак, связи различаются:

1. Однофакторные (простые) связи обычно называются парными (т.к.        рассматривается пара признаков). Например, корреляционная связь между    прибылью и производительностью труда.

2.  Многофакторная (множественная) связь - имеют в виду, что все факторы действуют комплексно, то есть одновременно и во взаимосвязи. Например, корреляционная связь между производительностью труда и уровнем организации труда, автоматизации производства, квалификации рабочих,  производственным стажем, простоями и другими факторными признаками. С помощью множественной корреляции можно охватить весь комплекс факторных признаков и объективно отразить существующие множественные связи.

В экономической практике не встречаются взаимосвязи, которые полностью можно описать при помощи формальных уравнений. Поэтому при изучении зависимости между признаками основными этапами изучения являются:

1. Выдвижение гипотезы о наличии связи между признаками.

2. Проверка факта наличия зависимости между признаками

3. Установление направления и выбор формы зависимости между признаками с помощью графических методов.

4. Установление тесноты зависимости между признаками.

5. Построение модели, определение параметров аналитической зависимости между признаками методом наименьших квадратов.

6. Оценка достоверности параметров аналитической зависимости и оценка точности ее результатов с помощью статистических критериев.

7. Экономическая интерпретация результатов и практическое использование полученной модели процесса.

Методы изучения взаимосвязи

Статистика изучает взаимосвязи при помощи системы методов, важнейшими среди которых являются:

1.     Метод аналитических группировок.

Это группировка данных, выявляющая взаимосвязи между изучаемыми явлениями и их признаками.  Чтобы выявить зависимость с помощью этого метода, нужно произвести группировку единиц совокупности по факторному признаку и для каждой группы вычислить среднее или относительное значение результативного признака. Это позволяет «сжать» информацию, полученную в ходе наблюдения, и на этой основе выявить закономерности, присущие изучаемому явлению. Это дает возможность визуальным путем определить характер и тесноту взаимосвязи. Сопоставляя затем изменения результативного признака по мере изменения факторного можно выявить направление, характер и тесноту связи между ними. Например, распределение по весу в зависимости от возраста.

Группировкой называется расчленение множества единиц изучаемой совокупности на группы по определенным существенным для них признакам.

Для определения количества групп, которые следует образовать из имеющейся совокупности признаков, необходимо использовать формулу Стерджесса,

n = 1 + 3,321 N,                                                         (1.1)

где n -  число групп, N – число единиц для всей совокупности, например,

А длина интервала находится по формуле:

i  =   x max  - x min                                           (1.2)

                  n

Пример аналитической группировки см. таблица 3.4 аналитической части.

2. Метод параллельных рядов.

Этот метод является одним из простейших. Для этого факторы, характеризующие результативный признак располагают в возрастающем или убывающем порядке (в зависимости от эволюции процесса и цели исследования), а затем прослеживают изменение величины результативного признака. Сопоставление и анализ расположенных таким образом рядов значений изучаемых величин позволяют установить наличие связи и ее направление. Зависимость между факторами и показателями может прослеживаться во времени (параллельные динамические ряды).

Например, данные о 10 предприятиях:

Для характеристики взаимосвязи факторный признак располагают в монотонно убывающем или возрастающем порядке, а показатели результата перемещаются в соответствии с факторным показателем.

3. Балансовый метод

Используется для отражения соотношений пропорций двух групп, взаимосвязанных и уравновешенных экономических показателей, итоги которых тождественны (например, обеспеченность ресурсами, полнота их использования).

Балансовый метод в статистике, важнейший метод обработки и анализа статистических данных, позволяет взаимно увязать ресурсы и их использование, выявить пропорции и взаимосвязи, складывающиеся в процессе воспроизводства.

  Всякий баланс состоит из 2 балансирующихся частей — приходной и расходной. В приходной части учитываются все ресурсы (запасы на начало года, производство, импорт и др.), а в расходной части — все виды использования (на производственные нужды, непроизводственные, потребление, экспорт, создание резервов и др.) и запасы на конец года.

Например, основной показатель развития ВВП проходит в своем движении 3 стадии: производство, распределение и перераспределение, конечное использование.

Взаимосвязь между отдельными стадиями движения ВВП и отдельными компонентами ВВП осуществляется при помощи балансового метода. Его суть заключается в том, что величина ВВП на всех трех стадиях должна быть одинакова

4. Графический метод.

Графиками в статистике называют условные изображения геометрическими или другими символами данных для их лучшего восприятия и чтения, а также для наглядной характеристики соотношений и связей между изучаемыми явлениями.

Придавая статистическим данным предметно-образное выражение, графики делают их более доступными для восприятия, чем непосредственно цифровое выражение этих данных.

Кроме того, графики позволяют представить статистические данные в общем виде и в сравнении друг с другом. Сами закономерности развития явления гораздо легче обнаруживаются и воспринимаются по изменениям таких зрительных образов, как линии, столбики, точки и т.д. Всё это делает статистические графики важным средством выражения, обобщения, анализа статистических данных, средством их широкой популяризации.

В основу классификации графиков положено различие полей графиков. Полем графика может служить либо чистая бумага, либо географическая (контурная) карта. С этой точки зрения различают диаграммы и статистические карты.

Диаграмма – графическое изображение статистических данных, наглядно показывающее соотношение между сравниваемыми величинами.

Все диаграммы делят на:

1.         Диаграммы сравнения

2.         Структурные диаграммы

3.         Динамические диаграммы

 Диаграммы сравнения предназначены для изображения различных совокупностей по какому-то одному изменяющемуся в пространстве признаку, т.е. в таких диаграммах сравниваются различные объекты по одному признаку. Наиболее распространенными подвидами этих диаграмм являются столбиковые  и полосовые (см. рис. 3.1 аналитической части).

Структурные диаграммы предназначены для сопоставления совокупности по составу, т.е. с их помощью характеризуется доля, удельный вес каждой части совокупности. Наиболее распространенными подвидами этих диаграмм являются столбиковые, секторные.

                                                                          Рис. 1.1                                                                    

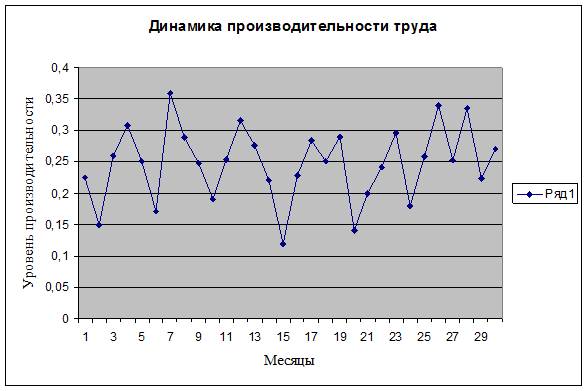
Динамические диаграммы – наиболее распространенный вид диаграмм. Он предназначен для показа изменения явления во времени. Наиболее распространенными подвидами этих диаграмм являются столбиковые, полосовые, круговые, квадратные, изобразительные.                            Рис 1.2

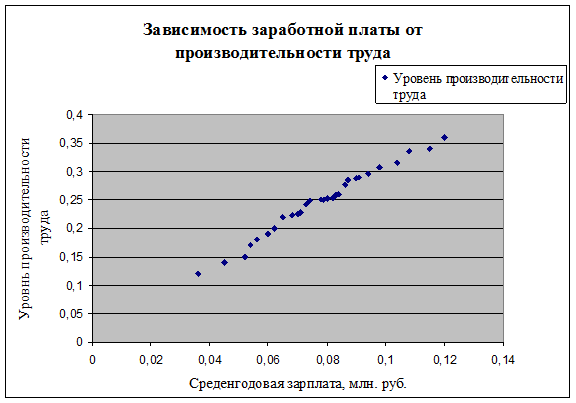
Статистические карты отражают статистико-географический разрез данных, то есть показывают размещение явления по территории.

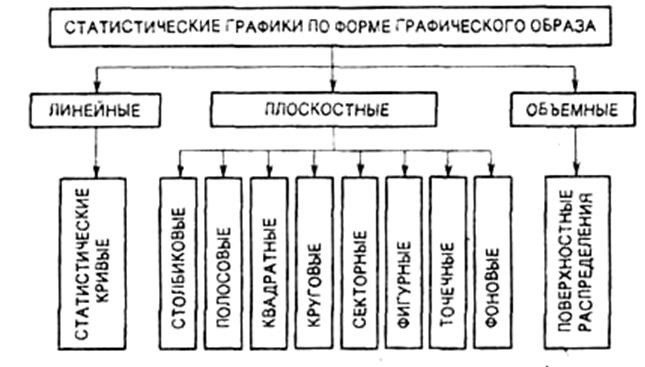
Классификация видов графиков

1.     Классификация статистических графиков по форме графического образа

Рис 1.1

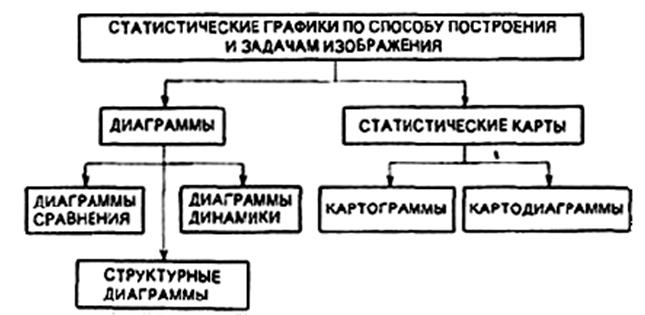
2.     Классификация статистических графиков по способу представления и задачам изображения    

Рис. 1.2                                                                                               

5.    Корреляционно-регрессионный анализ

Корреляционная связь – связь, проявляющаяся при достаточно большом числе наблюдений в виде определенной зависимости между средним значением результативного признака и признаками-факторами.

Изучение корреляционных связей сводится в основном к решению следующих задач:

Ø        выявление наличия (или отсутствия) корреляционной связи между изучаемыми признаками. Эта задача может быть решена на основе параллельного сопоставления (сравнения) значений  х  и  у  у  n  единиц совокупности; с помощью группировок; построения и анализа специальных корреляционных таблиц; а также построения диаграмм рассеяния;

Ø        измерение тесноты связи между двумя (и более) признаками с помощью специальных коэффициентов. Эта часть исследования называется корреляционный анализ;

Ø        определение уравнения регрессии – математической модели, в которой среднее значение результативного признака  у  рассматривается как функция одной или нескольких переменных – факторных признаков. Эта часть исследования называется регрессионный анализ.

Задача корреляционного анализа – измерение тесноты связи между варьируемыми признаками и оценка факторов, оказывающих наибольшее влияние.

Задача регрессионного анализа – выбор типа модели (формы связи), устанавливающих степени влияния независимых переменных.

Связь признаков проявляется в их согласованной вариации, при этом одни признаки выступают как факторные, а другие – как результативные. Причинно-следственная связь факторных и результативных признаков характеризуется по степени:

· тесноты;

· направлению;

· аналитическому выражению.

Регрессионный анализ

 Для оценки параметров уравнений регрессии наиболее часто используется метод наименьших квадратов (МНК), суть которого заключается в следующем требовании: искомые теоретические значения результативного признака 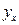 должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических (фактических) значений, т.е.

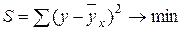.                                    (1.3)

При изучении связей показателей применяются различного вида уравнения прямолинейной и криволинейной связи. Так, при анализе прямолинейной зависимости применяется уравнение:

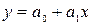                                                                                  (1.4)

Наиболее часто используемая форма связи между коррелируемыми признаками – линейная, при парной корреляции выражается уравнением (1.4),  где а₀ – среднее значение в точке  x=0, поэтому экономической интерпретации коэффициента нет; а₁ – коэффициент регрессии, показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.

Система нормальных уравнений МНК для линейной парной регрессии имеет следующий вид:

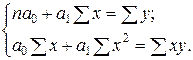                                                          (1.5)

Отсюда можно выразить коэффициенты регрессии:

                                            ;                                        

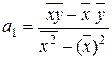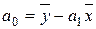                                            .                                   (1.6)

Для практического использования регрессионных моделей необходима проверка их адекватности. При численности объектов анализа до 30 единиц возникает необходимость проверить, насколько вычисленные параметры характерны для отображаемого комплекса условий, не являются ли полученные значения параметров результатом действия случайных причин. Значимость коэффициентов регрессии применительно к совокупности  n<30  определяется с помощью t-критерия Стьюдента. При этом вычисляются фактические значения t-критерия:

для параметра а₀: 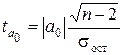                         ,                                (1.7)

для параметра а₁: 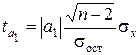                         .                             (1.8)

В формулах (1.7) и (1.8):

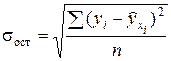 - среднее квадратическое отклонение результативного признака y_i от выровненных значений 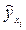.                                               (1.9)

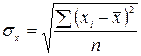 - среднее квадратическое отклонение факторного признака 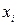 от общей средней 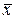.                                                                               (1.10)

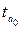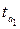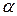Полученные по формулам (1.7) и (1.8) фактические значения и сравниваются с критическим , который получают по таблице Стьюдента с учетом принятого уровня значимости  и числа степеней свободы ν (ν=n-k-1), где n – число наблюдений, k – число факторов, включенных в уравнение регрессии). Рассчитанные параметры а₀ и а₁ уравнения регрессии признаются типичными, если t фактическое больше t критического.

 Корреляционный анализ позволяет установить тесноту связи между факторами и решить следующие задачи:

·        ответить на вопрос: существует ли связь?

·        выявить изменение связи в различных ситуациях реальных данных;

·        определить наиболее значимые факторы в результативном признаке;

Различают:

·        парную корреляцию – это зависимость между результативным и факторным признаком;

·        частную корреляцию – это зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков;

·        множественную – многофакторное влияние в статической модели .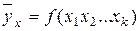

К показателям тесноты связи относятся:

·        коэффициент детерминации;

·        линейный коэффициент корреляции.

Теснота связи при линейной зависимости измеряется с помощью линейного коэффициента корреляции, который рассчитывается по одной из формул: 

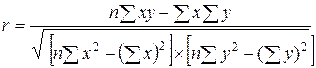 или 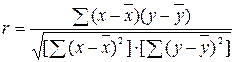. (1.11)

Корреляционный анализ выполняет оценку адекватности регрессионной модели, но путем установления тесноты связи.

Оценка линейного коэффициента корреляции

Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента. Для этого определяется фактическое значение критерия 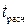:  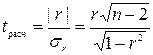                                            ,                                      (1.12)

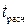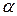Вычисленное по формуле (1.12) значение  сравнивается с критическим , который получают по таблице Стьюдента с учетом принятого уровня значимости  и числа степеней свободы ν.

Коэффициент корреляции считается статистически значимым, если t_расч превышает ( t_расч > ).

Универсальным показателем тесноты связи является теоретическое корреляционное отношение:

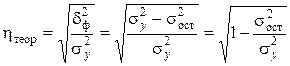,                 (1.13)

где 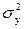    – общая дисперсия эмпирических значений y, характеризует вариацию результативного признака за счет всех факторов, включая х;

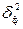 – факторная дисперсия теоретических значений результативного признака, отражает влияние фактора х на вариацию у;

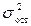 – остаточная дисперсия эмпирических значений результативного признака, отражает влияние на вариацию у всех остальных факторов кроме х.

Оценка связи на основе теоретического корреляционного отношения (шкала Чеддока)

Для линейной зависимости теоретическое корреляционное отношение тождественно линейному коэффициенту корреляции, т.е. η = |r|.

Множественный коэффициент корреляции в случае зависимости результативного признака от двух факторов вычисляется по формуле:

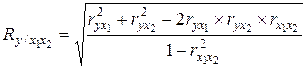,             (1.14)

где     – парные коэффициенты корреляции между признаками.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: .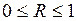

Значимость коэффициента множественной детерминации, а соответственно и адекватность всей модели и правильность выбора формы связи можно проверить с помощью критерия Фишера:

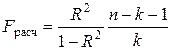,                                           (1.15)

где    R² – коэффициент множественной детерминации (R² );

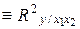          k – число факторных признаков, включенных в уравнение регрессии.

Связь считается существенной, если    F_расч > F_табл   – табличного значения F-критерия для заданного уровня значимости  α  и числе степеней свободы ν₁ = k, ν₂ = n – k – 1.

Частные коэффициенты корреляции характеризуют степень тесноты связи результативного признака и фактора, при элиминировании его взаимосвязи с остальными факторами, включенными в анализ. В случае зависимости у от двух факторных признаков частные коэффициенты корреляции рассчитываются:

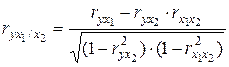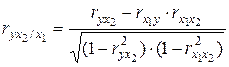  ;       ,             (1.16)

где    r – парные коэффициенты корреляции между указанными в индексе переменными.

В первом случае исключено влияние факторного признака х₂, во втором – х_1.

6.    Индексный метод

Индекс – это относительный показатель, который характеризует соотношение величин какого-либо сложного экономического явления во времени и пространстве.

Основным элементом индексного отношения является индексируемая величина. Под индексируемой величиной понимается значение признака статистической совокупности, изменение которой является объектом изучения. Поскольку объекты изучения индексов весьма разнообразны, то они широко применяются в экономической практике.

Задачи индексного метода:

1.         Индексы позволяют измерить результаты изменения не только однотипных явлений, но и совокупностей, состоящих из элементов непосредственно несоизмеримых;

2.         Позволяют измерить влияние факторов в динамике;

3.         Позволяют измерить влияние структуры явлений на величину индексируемого признака.

Классификация индексов

По степени охвата единиц совокупности:

1.     Индивидуальные  - характеризуют изменения величины элемента одного явления;

2.     Общие – характеризуют изменения статистического показателя в целом по совокупности

В зависимости от характера исследуемого объекта:

1. Индекс количественных показателей – индексы физического объема промышленной и сельскохозяйственной продукции, физического объема товарооборота, национального дохода и др.

2. Индекс качественных показателей – индексы курса валют, цен, себестоимости, производительности труда, средней заработной платы, урожайности и др.

Если индексы охватывают не все элементы сложного явления, а лишь часть, то их называют групповыми или субиндексами (например, индексы продукции по отдельным отраслям промышленности).

Индексный метод имеет свою терминологию и символику. Каждая индексируемая величина имеет обозначение:

q – количество (объем) какого-либо продукта в натуральном выражении;

p – цена единицы товара;

z – себестоимость единицы продукции;

t - затраты времени на производство единицы продукции (трудоемкость);

T – общие затраты времени (T=tq) или численность работников;

w – выработка продукции в стоимостном выражении на одного работника или единицу времени;

pq – общая стоимость произведенной продукции данного вида или общая стоимость проданных товаров данного вида (товарооборот, выручка).

Чтобы различать, к какому периоду относятся индексируемые величины, принято возле символа индекс внизу справа ставить подстрочные знаки: 1 – для сравниваемых (текущих, отчетных) периодов и 0 – для периодов, с которыми производится сравнение.

Например,    

        __    __       ∑ W₁ T₁       ∑ W₀ T₀

I_W = W₁ : W₀  =       ∑T₁                  ∑ T₀       - индекс производительности труда, где

W = q/Т, где W – средняя выработка, q – количество произведенной продукции, T – численность работников.

II. Практическая часть

Имеются следующие выборочные данные по предприятиям одной из отраслей промышленности региона в отчетном году (выборка 20%-ая механическая)

                                                                                                                 Таблица 2.1

Задание 1.

Признак – среднегодовая заработная плата (определите как отношение фонда заработной платы к среднесписочной численности работников). Число групп – пять. Решение. Рассчитаю среднюю заработную плату как отношение фонда заработной платы к среднесписочной численности работников, полученные данные занесу в таблицу:

Таблица 2.2

Построю интервальный вариационный ряд, величина интервала которого находится по формуле:

i  =   x max  - x min

                  n

i =     0,12 – 0,036    =  0,0168  млн.руб.

                  5  

Отсюда путем прибавления величины интервала к минимальному уровню признака в группе получу следующие группы предприятий по среднегодовой заработной плате:

Распределение предприятий по среднегодовой заработной плате

Таблица 2.3

Составлю таблицу аналитической группировки.

              Таблица 2.4

Для сгруппированных данных используется формула средней арифметической взвешенной:

_        ∑ х f

х   =     ∑ f     , где f – частость, тогда:                                                       

_        0,133*3 + 0,365*6 + 0,945*12 + 0,46*5 + 0,447*4 

х  =                                       30                                               =  0,601 млн. руб.

Значит, среднегодовая заработная плата равна 0,601 млн. руб.

Задание 2

Связь между признаками – уровень производительности труда (рассчитайте как отношение выпуска продукции к среднесписочной численности работников) и среднегодовая заработная плата.

Решение.

Рассчитаю уровень производительности труда и занесу данные в таблицу 2.4.

Измерю тесноту корреляционной связи между производительностью труда и среднегодовой заработной платой с помощью коэффициента детерминации и эмпирического корреляционного отношения. Для этого определю уровень производительности труда как факторный признак (Х), а среднегодовую заработную плату как результативный (Y), затем рассчитаю необходимые данные:    _

1.     (Yi - Y)² , где Yi – среднегодовая заработная плата по каждому предприятию отдельно, а

     _

    Y –среднегодовая заработная плата по всем 30 предприятиям, рассчитываемая по формуле                         

_       ∑ y 

Y =    N    - где N число предприятий всей совокупности (в данном случае, 30)

           _     _   

4.      (Yi - Y)²

_                                       _     _                                     _

Y = 2,35/30 = 0,078; ∑ (Yi - Y)²  = 0,0589524;  ∑(Yi - Y)² = 0,115461, тогда:

 Таблица 2.5

Отсюда найду дисперсию,         

             ∑(y_i – y )²        

σ²  =           n                -  невзвешенная (простая);             (2.1)

             ∑(y_i – y )² f

σ²  =           ∑f             - взвешенная.                                     (2.2)

сначала общую (2.1):

            0,0115461 

                   σ²    =           30        =  0,0003849

затем межгрупповую (2.2):

        0,001156* 3+0,000289*6+0,056169*12+0,000196*5+0,001142*4 

σ² =                                            30                                                           = 0,000228

Коэффициент детерминации равен отношению межгрупповой дисперсии к общей:

                              σ_х²  

                     η²  =  σ²                                                                                      (2.3)

 0,0002280

           η²  =   0,0003849    =  0,5924

Корень квадратный из коэффициента детерминации называется эмпирическим корреляционным отношением.

Значит, эмпирическое корреляционное отношение:

 η  =  0,7697

Вывод: коэффициент детерминации   η²  =  0,5924 показывает, что вариация среднегодовой заработной платы на 59,24 % зависит от вариации уровня производительности труда, а остальные 40,76 % зависят от других факторов. Эмпирическое корреляционное отношение η показывает тесноту корреляционной связи, т.к. в данной задаче η  = 0,7697, то связь сильная, т.к. попадает в интервал от 0,7 до 0,9 по таблице Чеддока.

Задание 3.

          По результатам выполнения задания 1 с вероятностью 0,954 определите:

1.     Ошибку выборки среднего уровня заработной платы и границы, в которых будет находиться средняя заработная плата в генеральной совокупности.

2.     Ошибку выборки доли организаций с уровнем среднегодовой заработной платы 86,4 тыс. руб. и более и границы, в которых будет находиться генеральная доля.

Решение

1.     При механическом отборе предельная ошибка выборки определяется по формулам:

            σ²          n

∆_Х = t   n   1 -   N       - для средней;                                                 (2.4)

               ω(1 – ω)           n

∆_ω  = t            n         1 -  N      - для доли, где                                         (2.5)

n – численность выборки;

N – численность генеральной совокупности;

ω  - выборочная доля, определяемая по формуле ω = m/n;

t – коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной вероятности;

σ²  - дисперсия выборочной совокупности.

Найду ошибку выборки среднего уровня заработной платы:

n – т.к. была произведена 20%-ая выборка, численность которой равна 30 предприятий, то численность генеральной совокупности равна 30*100% / 20%  = 150 предприятий;

N – 150 предприятий;

t – т.к. в данной задаче задана вероятность 0,954, то, согласно таблице Лапласа, коэффициент доверия равен 2, тогда:

                 0,0003849              30

∆_Х = 2            30        * (1 - 150)  =  0,00641, значит ошибка выборки среднего уровня заработной платы 0,641%.

Найду границы, в которых будет находиться средняя заработная плата в генеральной совокупности, по формуле:

_

х  = х ± ∆_Х,  где х – средняя заработная плата.                                 (2,6)

Средняя заработная плата по 30 предприятиям составляет 2,35/30 = 0,078,

                   _{__}  

значит, х   = 0,078 ± 0,00641 или:

0,0716 < 0,078 < 0,0844

Средняя заработная плата составляет 0,078 млн. руб. или 0,078*1000 = 78  тыс. руб. в год. С вероятностью 0,954 можно утверждать, что средняя заработная плата будет находиться в пределах 0,0716 < 0,078 < 0,0844.

2. Для определения доли предприятий с уровнем среднегодовой заработной платы 86,4 тыс. руб. и более, в таблице 2.3 проведу ранжирование данных (среднегодовая заработная плата) по возрастанию и переведу единицы измерения с млн. руб. на тыс. руб.

Из таблицы видно, что количество предприятий со среднегодовой заработной платой больше 86,4 тыс. руб. составляет 9 штук. Отсюда найду долю предприятий в общей совокупности:  ω = m/n, где m – доля единиц, обладающих признаком.

ω = 9/30 = 0,3

Ошибку выборки вычислю по формуле 2.5

                0,3∙0,7          9

∆ω = 2        30       1 - 30    =  0,14 или 14%

Найду границы, в которых будет находиться генеральная доля:

ω - ∆ω ≤ р ≤ ω + ∆ω

0,16 ≤ р ≤ 0,44

С вероятностью 0,954 можно утверждать, что доля предприятий с уровнем среднегодовой заработной платы 86,4 тыс. руб. и выше будет находиться в пределах 0,16 ≤ р ≤ 0,44.

Задание 4.

Имеются следующие данные по организации:

Определите:

1. Уровень производительности труда, показатель эффективности использования основных производственных фондов (фондоотдачу), фондовооруженность труда за каждый период.

2. Абсолютное и относительное изменение всех показателей в отчетном периоде по сравнению с базисным периодом.

 Результаты расчетов представьте в таблице.

3. Взаимосвязь индексов фондоотдачи, фондовооруженности и производительности труда.

4. Абсолютное изменение выпуска продукции в результате изменения численности работников, производительности труда и обоих факторов вместе. Сделайте выводы.

Решение.

1. Уровень производительности труда – результативность конкретного живого труда, эффективность целесообразной деятельности людей по созданию продукта в течение определенного промежутка времени, рассчитывается как отношение выпуска продукции к среднесписочной численности работников, значит,

для базисного периода это:

W₀ = 14,4/130 = 0,1108;

Для отчетного:

W₁ = 15,8/125 = 0,1264.

Из расчетов видно, что уровень производительности труда отчетного периода увеличился по сравнению с базисным.

Фондоотдача – это показатель эффективности использования основных производственных фондов, рассчитываемый как отношение выпуска продукции к стоимости основных производственных фондов.

V₀ = 14,4/16,0 = 0,9

V₁ = 15,8/18,0 = 0,87

В базисном периоде фондоотдача была выше, чем в отчетном, значит, фонды эффективнее использовались в базисном периоде.

          Фондовооруженность – это показатель количества производственных фондов, приходящихся на одного занятого в материальном производстве, определяемый отношением стоимости основных производственных фондов к среднесписочной численности работников.

Ф₀ = 16,0/130 = 0,123

Ф₁ = 18,0/125 = 0,144 

Т.к. фондовооруженность в отчетном периоде выше, чем в базисном, это означает, что в отчетном периоде основных производственных фондов на каждого работника приходится больше.

1.     Абсолютное изменение – рассчитывается как разница между периодами (в данном случае, разница между отчетным и базисным периодом)

Относительное изменение – рассчитывается как отношение двух периодов (отношение отчетного периода к базисному), например, найду изменения по выпуску продукции:

Абсолютное:         15,8 – 14,4 = 1,4

Относительное:  15,8/14,4 = 1,097*100% = 109,7%, и так далее для других показателей.

Исходя из полученных данных, можно судить о том, что у выпуска продукции и среднегодовой стоимости основных производственных фондов наблюдается абсолютный прирост, а в среднесписочной  численности работников – абсолютное снижение (т.к. - 5 < 1). Относительное изменение говорит об увеличении выпуска продукции и среднегодовой стоимости основных производственных фондов (темп роста), и об уменьшении численности работников (темп снижения).

2.     Для определения взаимосвязи искомых индексов, рассчитаю эти индексы по формулам.

        __    __       ∑ W₁ T₁       ∑ W₀ T₀

I_W = W₁ : W₀  =       ∑T₁                  ∑ T₀       - индекс производительности труда, где

W = q/Т, где W – средняя выработка, q – количество произведенной продукции, T – численность работников.

          15,8

W₁ =   125  = 0,1264 - средняя выработка продукции за отчетный период;

          14,4

W₀ =  130   = 0,1108 – средняя выработка продукции за базисный период;

          0,1264∙125     0,1108∙130

I_W =         125                  130        =  1,1408.

Это означает, что уровень производительности труда отчетного периода по сравнению с базисным периодом возрос на 114,08 – 100% = 14,08%.

Индекс фондоотдачи:

          Q₁          Q₀

Iv = СФ₁  : СФ₀  , где Q – выпуск продукции, СФ – среднегодовая стоимость основных производственных фондов.

Iv = 0,87/0,9 = 0,967,

Это означает, что в отчетном периоде на каждый рубль основных производственных фондов получали 0,87 рубля продукции, а в базисном периоде на каждый рубль основных фондов получали 0,9 руб. продукции. А уровень фондоотдачи снизился на 100 – 96,7% = 3,3 %. Отсюда можно сделать вывод, что производство продукции происходит в ущерб предприятию, затраты на основные производственные фонды не окупаются.

Индекс фондовооруженности:

         СФ₁      СФ₀ 

Iф =    Т₁    :    Т₀    

          0,144   

Iф =   0,123  = 1,171

Это означает, что в базисном периоде на каждого работника предприятия приходилось 0,123 млн. руб. основных производственных фондов, а в отчетном 0,144 млн. руб. Уровень фондовооруженности возрос на 117,1 – 100% = 17,1%. Отсюда можно сделать вывод, что уровень фондовооруженности повысился за счет уменьшения числа работников и увеличения основных производственных фондов, что, в свою очередь, привело к увеличению выпуска продукции.

Взаимосвязь индексов фондоотдачи, фондовооруженности и производительности труда.

Взаимосвязь между тремя основными показателями хозяйственной деятельности предприятия - фондоотдачей, фондовооружённостью, производительностью труда. Если перемножить результаты фондоотдачи и фондовооружённости, получим результат уровня производительности труда одного работника. Например, фондоотдачу можно представить как частное от деления производительности труда на фондовооруженность, следовательно, фондоотдача прямо пропорциональна производительности труда и обратно пропорциональна его фондовооруженности. Поэтому для повышения фондоотдачи  необходимо, чтобы темпы роста производительности труда опережали темпы роста его фондовооруженности.

I_W = Iv ∙ Iф = 0,967 ∙ 1,171 = 1,140

4.  1). Абсолютное изменение выпуска продукции в результате изменения численности работников и производительности труда:

∆_WT = ∑ W₁ T₁ - ∑ W₀ T₀

∆_WT = 0,1264 – 0,1108 = 0,0156 млн. руб.

За счет взаимодействия обоих факторов выпуск продукции увеличился на 0,0156 млн. руб.

2). Абсолютное изменение выпуска продукции в результате изменения численности работников:

∆^T_WT = ∑ W₀ T₁ - ∑ W₀ T₀ = 0,1108∙125 – 0,1108∙130 = 13,85 – 14,404 = - 0,554 млн. руб.

Значит, за счет уменьшения числа работников на 5 человек, выпуск продукции снизился на 0,554 млн. руб.

3). Абсолютное изменение выпуска продукции в результате изменения производительности труда:

∆^W_WT = ∑ W₁ T₀ - ∑ W₀ T₀  = 0,1264∙130 – 0,1108∙130 = 16,432 – 14,404 = 2,028 млн. руб.

Значит, в результате увеличения производительности труда на 0,0156 млн. руб. выпуск продукции увеличился на 2,028 млн. руб.

 III. Аналитическая часть

Имеются следующие выборочные данные по предприятиям одной из отраслей промышленности региона в отчетном году (выборка 20%-ая механическая).

Выявить зависимость, измерить тесноту связи между признаками (производительностью труда и среднегодовой заработной платой)

Решение:

Для изучения структуры предприятий по выпуску продукции, построю интервальный вариационный ряд. Величина интервала находится по формуле:

i  =   x max  - x min

                  n

i =     0,356 – 0,121    = 0,047 млн.руб.

                    5  

Отсюда путем прибавления величины интервала к минимальному уровню признака в группе получу следующие группы предприятий по производительности труда:

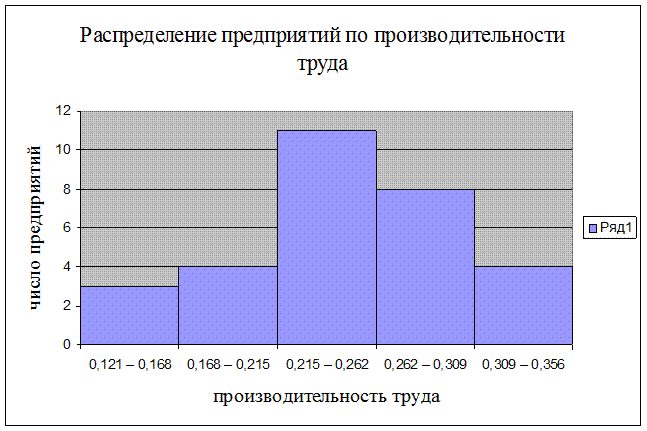
                                                                    Таблица 3.1

Распределение предприятий по производительности труда

Данные группировки показывают, что низкую производительность труда имеют только 10% предприятий.

Рис. 3.1

Для изучения структуры предприятий по средней заработной плате построю интервальный вариационный ряд. Найду величину интервала:

i = (0,122 – 0,042)/ 5= 0,016

Получаю следующие группы предприятий по среднегодовой заработной плате:

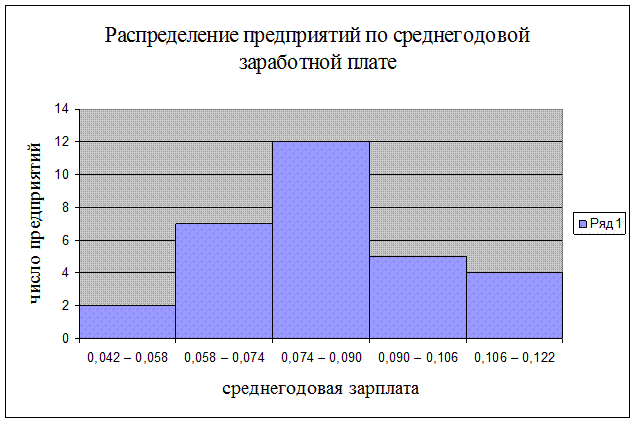
Таблица 3.2

Распределение предприятий по среднегодовой заработной плате

Данные группировки показывают, что в 40% предприятий среднегодовая заработная плата составляет свыше 74 тыс. руб.

Рис. 3.2

Мода – значение признака, наиболее часто встречающееся в изучаемой совокупности.

Моду можно определить графически и математически:

                                           f_Mo  -  f_{Mo-1___________} , где               

М_о  =  х_Мо  +  i_Mo  (f_Mo  -  f_Mo-1) + (f_Mo  -  f_Mo+1)

М_о  - мода;

х_Мо – нижняя граница модального интервала;

i_Mo  - величина модального интервала;

f_Mo  - частота модального интервала;

f_Mo-1  - частота интервала, предшествующего модальному;

f_Mo+1  - частота интервала, следующего за модальным.

                                       _____12 - 7___

М_о  = 0,074 + 0,016*    (12 - 7) + (12 - 5)   =  0,0807 млн. руб.

Для изучения связи между явлениями и их признаками построю корреляционную таблицу и аналитическую группировку.

Корреляционная таблица – это специальная комбинационная таблица, в которой представлена группировка по двум взаимосвязанным признакам: факторному (Х, производительность труда) и результативному (Y, среднегодовая заработная плата).

Концентрация частот около диагонали матрицы данных свидетельствует о наличии корреляционной связи между признаками.

Построю корреляционную таблицу, образовав, пять групп по факторному и результативному признакам.

Таблица 3.3

Распределение предприятий

по средней заработной плате  и производительности труда

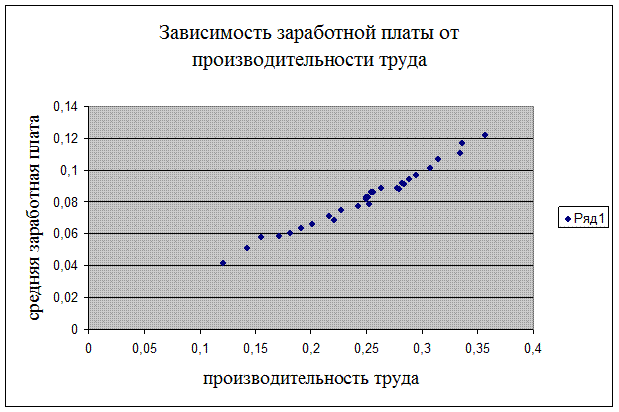
Как видно из таблицы 3.3, распределение числа предприятий произошло вдоль диагонали, проведенной из левого верхнего угла в правый нижний угол таблицы, т.е. увеличении признака «производительность труда» сопровождается увеличением признака «среднегодовая заработная плата». Характер концентрации частот по диагонали корреляционной таблицы свидетельствует о наличии прямой тесной корреляционной связи между изучаемыми признаками.

                                                                                  Рис. 3.3

Аналитическая группировка позволяет изучать взаимосвязь факторного и результативного признаков.

Таблица 3.4

Для установления наличия и характера связи между заработной платой и производительностью труда по данным таблицы 3.4 построю итоговую аналитическую таблицу:

Таблица 3.5

Зависимость среднегодовой заработной платы от производительности труда

Данные таблицы 3.5 показывают, что с ростом производительности труда увеличивается и среднегодовая заработная плата. Следовательно, между исследуемыми признаками существует прямая корреляционная зависимость. Теснота связи может быть измерена эмпирическим корреляционным отношением.

Показатели вариации

Для измерения степени колеблемости отдельных значений признака от средней исчисляются основные обобщающие показатели вариации: дисперсия, среднее квадратическое отклонение и коэффициент вариации.

Дисперсия (σ²) – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической.

В зависимости от исходных данных дисперсия вычисляется по формуле средней арифметической простой или взвешенной.

Коэффициент детерминации равен отношению межгрупповой дисперсии к общей и показывает долю общей вариации результативного признака, обусловленную вариацией группировочного признака (см. формулы 2.1 – 2.3 практической части)(ежгрупповой дисперсии к общей:                                                  дится больше.

сь в базисном периоде.ние опреде

Корень квадратный из коэффициента детерминации называется эмпирическим корреляционным отношением.

          Для сравнения размеров вариации различных признаков, а также для сравнения степени вариации одноименных признаков в нескольких совокупностях исчисляется относительный показатель вариации – коэффициент вариации (V), который представляет собой отношение среднего квадратического отклонения к средней арифметической:               

          σ_ 

  V =  х     ∙ 100%                                                                                                (3.4)

Найду дисперсию.

Для этого дополню таблицу  3.4 следующими графами:

1. Выпуск продукции в среднем по группе

                                                                                 _       ∑ Y

2. Фонд заработной платы в среднем по группе Yi  =  n   , n – число п/п в группе

                 _

2.     (Yi - Y)² , где Yi – фонд заработной платы по каждому предприятию отдельно, а

     _

    Y – средний фонд заработной платы по всем 30 предприятиям, рассчитываемый  по формуле                         

_       ∑ y 

Y =    N    - где N число предприятий всей совокупности (в данном случае, 30)

           _     _   

4.      (Yi - Y)²

_                                         _     _                                     _

Y = 2,465/30 = 0,082; ∑ (Yi - Y)²  = 0,002743;  ∑(Yi - Y)² = 0,01047909, тогда:

Таблица 3.6

Отсюда найду дисперсию,

сначала общую (2.1):

            0,01047909

                   σ²    =            30          =  0,000349

затем межгрупповую (2.2):

           0,001225*2+0,000324*7+0,000001*12+0,000169*5+0,001024*4 

σ²    =                                                  30                                                    = 0,000322

Найду коэффициент детерминации (2.3):

                              0,000322

                     η²  =  0,000349 =  0,9226         

Найду эмпирическое корреляционное отношение:

                      η  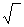=   η²  =  0,961                                             

Найду коэффициент вариации (3.4):

Для этого вычислю среднее квадратическое отклонение σ = 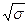²_общ. = 0,0187

                           0,0187   

                   V =   0,082  ∙ 100% = 22,81 %

Выводы: среднегодовая заработная плата – 0,082 млн. руб. коэффициент вариации 22,81% показывает, что вариация заметная, выборочная совокупность однородная, средняя надежная. Коэффициент детерминации 0,9226 показывает, что вариация фонда заработной платы на 92,26 % зависит от вариации выпуска продукции, а остальные 7,74 % объясняются другими  факторами.

Эмпирическое корреляционное отношение η  показывает тесноту корреляционной связи, т.к. в данной задаче η  = 0,961, то связь очень тесная, т.к. попадает в интервал более 0,9 по таблице Чеддока.

Заключение

Итак, в этой работе я показала особую значимость изучения взаимосвязей производственных показателей фирмы, для улучшения производительности труда, для понимания взаимосвязи основных показателей фирмы, и, как следствие, увеличения прибыли предприятия.

В аналитической части, путем метода параллельных рядов, метода группировок, а также графическим методами была выявлена зависимость между фондом заработной платы и выпуском продукции на примере 30 предприятий одной из отраслей промышленности.

В практической части выявлена и объяснена сильная зависимость между среднегодовой заработной платой и выпуском продукции с помощью индексного метода, метода аналитической группировки и др.

Использованная литература:

1. Гусаров В.М. - Статистика: Учеб. Пособие для вузов. – М.: ЮНИТИ – ДАНА, 2001. - 463 с.

2. Гусаров В.М. Теория статистики: Учебн. пособие для вузов. – М.: Аудит, ЮНИТИ, 1998. – 247 с.

3. Общая теория статистики: Учебник/под редакцией чл.-кор. РАН И.И. Елисеевой. – 4-е изд., перераб. и доп. – М.: Финансы и статистика, 2001. – 480 с.

4. Практикум по статистике: Учеб. Пособие для вузов/Под ред. В.М. Симчеры /ВЗФЭИ. – М.: ЗАО «Финстатинформ», 1999. – 259 с.

5. Прикладная статистика. Учебник. / А.И.Орлов.- М.: Издательство «Экзамен», 2004. -  656 с.

6. Статистика: Методические указания по выполнению курсовой работы для студентов III курса, обучающихся по специальности «Финансы и кредит». – М.: Вузовский учебник, 2005. – 81 с.

7. Теория статистики: Учебник/Под ред. проф. Р.А. Шмойловой. – М.: Т33 Финансы и статистика, 1998. – 464 с.

Интернет-ресурсы:

1. http://cnit.ssau.ru/iatp/work/barinova/P3.htm

2. http://www.ostu.ru/vzido/resurs/statistika/4semester/up.prom.stat3.htm