ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ
ИНСТИТУТ
Филиал
в г.Уфе
Кафедра
математики и информатики
КОНТРОЛЬНАЯ
РАБОТА
по
дисциплине «Эконометрика»
Вариант
13
Исполнитель:
специальность
группа
№ зачетной книжки
Преподаватель:

Практическая задача 1
1.1.
Условие и исходные данные 
Вариант
выданного задания – 13.
Условие
задачи: По предприятиям легкой промышленности региона получена информация,
характеризующая зависимость объема выпуска продукции (Y,млн. руб.) от объема
капиталовложений(X,
млн. руб.)
Таблица 1.
|
Y
|
176
|
170
|
156
|
172
|
162
|
160
|
166
|
|
X
|
150
|
154
|
146
|
134
|
132
|
126
|
133
|
Требуется:
1. Для характеристики Y от Х построить следующие модели:
- линейную;
- степенную;
- показательную;
- гиперболическую.
2. Оценить каждую модель,
определив:
- индекс корреляции,
- среднюю относительную
ошибку,
- коэффициент
детерминации,
- F-критерий Фишера.
3. Составить сводную
таблицу вычислений, выбрать лучшую модель, дать интерпретацию рассчитанных
характеристик.
4. Рассчитать прогнозные
значения результативного признака, если прогнозное значение фактора увеличится
на 10% относительно среднего уровня.
5. Результаты расчетов
отобразить на графике.
1.2
Решение задачи
1.
Построение линейной модели парной регрессии
|
Таблица
1.2
|
|
t
|
y
|
x
|
y * x
|
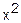
|
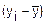
|
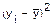
|
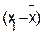
|
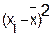
|
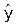
|
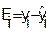
|
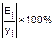
|
|
1
|
176
|
150
|
26400
|
22500
|
10
|
100
|
10,71
|
114,80
|
168,80
|
7,20
|
4,09
|
|
2
|
170
|
154
|
26180
|
23716
|
4
|
16
|
14,71
|
216,51
|
169,85
|
0,15
|
0,09
|
|
3
|
156
|
146
|
22776
|
21316
|
-10
|
100
|
6,71
|
45,08
|
167,75
|
-11,75
|
-7,54
|
|
4
|
172
|
134
|
23048
|
17956
|
6
|
36
|
-5,29
|
27,94
|
164,62
|
7,38
|
4,29
|
|
5
|
162
|
132
|
21384
|
17424
|
-4
|
16
|
-7,29
|
53,08
|
164,10
|
-2,10
|
-1,29
|
|
6
|
160
|
126
|
20160
|
15876
|
-6
|
36
|
-13,29
|
176,51
|
162,53
|
-2,53
|
-1,58
|
|
7
|
166
|
133
|
22078
|
17689
|
0
|
0
|
-6,29
|
39,51
|
164,36
|
1,64
|
0,99
|
|
Итого:
|
1162
|
975
|
162026
|
136477
|
0
|
304
|
0,00
|
673,43
|
1162
|
0
|
-0,95
|
|
Ср.н
|
166
|
139,29
|
23146,57
|
19496,71
|
0,00
|
43,43
|
0,00
|
96,20
|
166
|
0
|
-0,14
|
Определим линейный коэффициент парной
корреляции по следующей формуле:
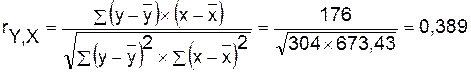

Можно сказать, что связь между объемом
капиталовложений Х и объемом выпуска продукции Y прямая, умеренная.
Уравнение линейной регрессии имеет
вид: 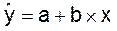
Значения параметров a и b линейной модели определим, используя
данные таблицы1.
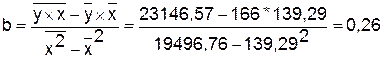
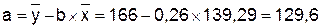
Уравнение линейной регрессии имеет
вид: 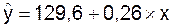
С увеличением объема
капиталовложений на 1 млн руб. объем
выпускаемой продукции увеличится в среднем на 260 тыс. руб. Это свидетельствует
о эффективности производства .
Рассчитаем коэффициент детерминации:
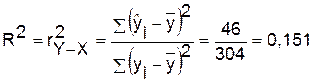
Вариация результата Y (объема выпуска продукции) на 15,1%
объясняется вариацией фактора Х (объем капиталовложений).
Оценку значимости уравнения регрессии
проведем с помощью F-критерия
Фишера:
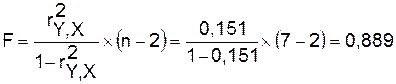
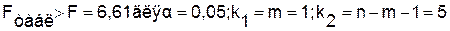
Cледовательно, принимается гипотеза Hо
о статистически незначимых параметрах этого уравнения. Этот результат можно
обьяснить сравнительно невысокой теснотой выявленной зависимости и небольшим
числом наблюдений.
Определим среднюю относительную
ошибку:
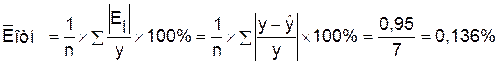
 В среднем расчетные значения
В среднем расчетные значения 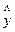 для линейной модели отличаются от фактических значений на
0,136%.
для линейной модели отличаются от фактических значений на
0,136%.
Найдем стандартную ошибку по формуле:
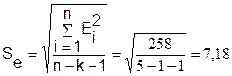
2. Построение степенной модели парной
регрессии.
Уравнение степенной имеет вид: 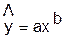
Для построения этой модели необходимо
произвести линеаризацию переменных. Для этого произведем логарифмирование обеих
частей уравнения: 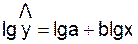
Таблица
1.3
|
|
Факт Y(t)
|
lg(Y)
|
Переменная X(t)
|
lg(x)
|
|
1
|
176
|
2,25
|
150
|
2,18
|
|
2
|
170
|
2,23
|
154
|
2,19
|
|
3
|
156
|
2,19
|
146
|
2,16
|
|
4
|
172
|
2,24
|
134
|
2,13
|
|
5
|
162
|
2,21
|
132
|
2,12
|
|
6
|
160
|
2,20
|
126
|
2,10
|
|
7
|
166
|
2,22
|
133
|
2,12
|
|
Итого:
|
1162
|
15,54
|
975
|
15,00
|
|
Сред.знач.
|
166
|
2,22
|
139,29
|
2,14
|
Обозначим Y 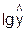 ,Х=
,Х=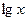 , А=
, А=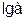 .
.
Тогда уравнение имеет вид:  - линейное уравнение регрессии.
- линейное уравнение регрессии.
Рассчитаем его параметры, используя
данные таблицы 1.4
Таблица 1.4
|
t
|
y
|
Y
|
x
|
X
|
YX
|
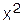
|
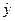
|
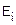
|
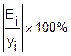
|
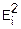
|
|
1
|
176
|
2,25
|
150
|
2,18
|
4,89
|
4,74
|
168,67
|
7,33
|
4,17
|
17,35
|
|
2
|
170
|
2,23
|
154
|
2,19
|
4,88
|
4,79
|
169,63
|
0,37
|
0,22
|
0,05
|
|
3
|
156
|
2,19
|
146
|
2,16
|
4,75
|
4,68
|
167,69
|
-11,69
|
-7,49
|
56,13
|
|
4
|
172
|
2,24
|
134
|
2,13
|
4,76
|
4,52
|
164,61
|
7,39
|
4,30
|
18,46
|
|
5
|
162
|
2,21
|
132
|
2,12
|
4,69
|
4,50
|
164,08
|
-2,08
|
-1,28
|
1,64
|
|
6
|
160
|
2,20
|
126
|
2,10
|
4,63
|
4,41
|
162,43
|
-2,43
|
-1,52
|
2,32
|
|
7
|
166
|
2,22
|
133
|
2,12
|
4,72
|
4,51
|
164,34
|
1,66
|
1,00
|
1,00
|
|
Итого:
|
1162
|
15,54
|
975
|
15,00
|
33,30
|
32,15
|
1161,45
|
0,55
|
-0,62
|
96,94
|
|
Сред.знач
|
166
|
2,22
|
139,29
|
2,14
|
4,76
|
4,59
|
165,92
|
0,08
|
-0,09
|
13,85
|
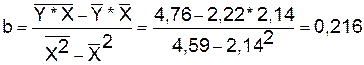
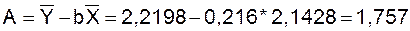
Перейдем к исходным переменным x и y, выполнив потенцирование данного
уравнения. 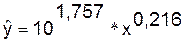
Получим уравнение степенной модели
регрессии: 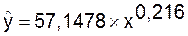
Определим индекс корреляции:
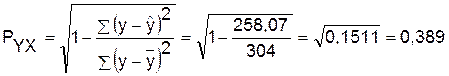
 Связь между показателем y и x умеренная.
Связь между показателем y и x умеренная.
Коэффициент детерминации равен 0,151:
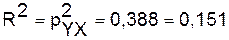
Вариация результата Y (объема выпуска продукции) на 15,1%
объясняется вариацией фактора Х (объем капиталовложений).
Оценку значимости уравнения регрессии
проведем с помощью F-критерия
Фишера:
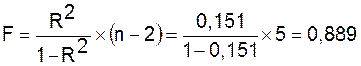
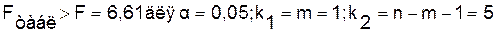
Следовательно, принимается гипотеза Hо о статистически незначимых параметрах
этого уравнения. Этот результат можно объяснить сравнительно невысокой теснотой
выявленной зависимости и небольшим числом наблюдений.
Определим среднюю относительную
ошибку:
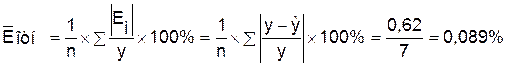
 В среднем расчетные значения
В среднем расчетные значения 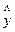 для линейной модели отличаются от фактических значений на
0,089%.
для линейной модели отличаются от фактических значений на
0,089%.
Найдем стандартную ошибку по формуле:
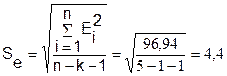
3. Построение
показательной функции.
Уравнение степенной имеет вид: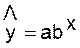
Для построения этой модели необходимо
произвести линеаризацию переменных. Для этого произведем логарифмирование обеих
частей уравнения: 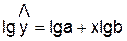
Обозначим Y 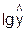 , B=
, B=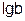 , А=
, А=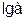 .
.
Тогда уравнение имеет вид: 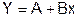 - линейное уравнение регрессии.
- линейное уравнение регрессии.
Рассчитаем его параметры, используя
данные таблицы 1.5
Таблица
1.5
|
t
|
y
|
x
|
y * x
|
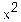
|
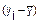
|
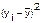
|
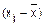
|
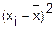
|
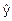
|
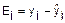
|
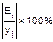
|
|
1
|
176
|
150
|
26400
|
22500
|
10
|
100
|
10,71
|
114,80
|
168,80
|
7,20
|
4,09
|
|
2
|
170
|
154
|
26180
|
23716
|
4
|
16
|
14,71
|
216,51
|
169,85
|
0,15
|
0,09
|
|
3
|
156
|
146
|
22776
|
21316
|
-10
|
100
|
6,71
|
45,08
|
167,75
|
-11,75
|
-7,54
|
|
4
|
172
|
134
|
23048
|
17956
|
6
|
36
|
-5,29
|
27,94
|
164,62
|
7,38
|
4,29
|
|
5
|
162
|
132
|
21384
|
17424
|
-4
|
16
|
-7,29
|
53,08
|
164,10
|
-2,10
|
-1,29
|
|
6
|
160
|
126
|
20160
|
15876
|
-6
|
36
|
-13,29
|
176,51
|
162,53
|
-2,53
|
-1,58
|
|
7
|
166
|
133
|
22078
|
17689
|
0
|
0
|
-6,29
|
39,51
|
164,36
|
1,64
|
0,99
|
|
Итого:
|
1162
|
975
|
162026
|
136477
|
0
|
304
|
0,00
|
673,43
|
1162
|
0
|
-0,95
|
|
Ср.знач.
|
166
|
139,29
|
23146,57
|
19496,71
|
0,00
|
43,43
|
0,00
|
96,20
|
166
|
0
|
-0,14
|
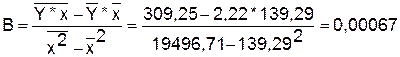
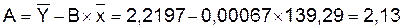
Уравнение будет иметь вид: Y=2,13+0,00067x
Перейдем к исходным уравнениям,
проведя потенцирование данного уравнения:
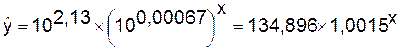
Определим индекс корреляции:
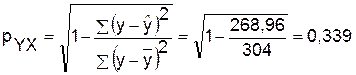
Связь между показателями y и фактором х умеренная.
Рассчитаем индекс детерминации:
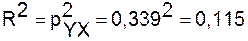
Вариация результата Y (объема выпуска продукции) на 11,5%
объясняется вариацией фактора Х (объем капиталовложений).
Оценку значимости уравнения регрессии
проведем с помощью F-критерия
Фишера:
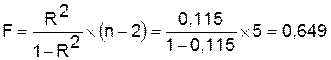
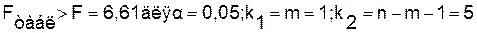
Cледовательно, принимается гипотеза Hо
о статистически незначимых параметрах этого уравнения. Этот результат можно
обьяснить сравнительно невысокой теснотой выявленной зависимости и небольшим
числом наблюдений.
Определим среднюю относительную
ошибку:
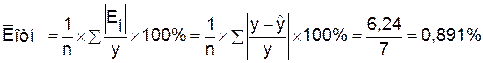
В среднем расчетные значения 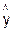 для линейной модели отличаются от фактических значений на
0,891%.
для линейной модели отличаются от фактических значений на
0,891%.
Найдем стандартную ошибку по формуле:
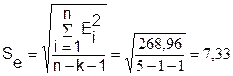
4.Построение гиперболической функции
Уравнение гиперболической функции: 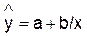
Произведем линеаризацию модели путем
замены X=1/x. В результате получим линейное
уравнение 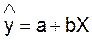 . Рассчитаем его параметры по данным таблицы 1.6
. Рассчитаем его параметры по данным таблицы 1.6
Таблица 1.6
|
t
|
y
|
x
|
X
|
yX
|
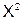
|
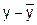
|
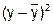
|
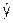
|
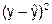
|
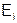
|
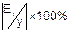
|
|
1
|
176
|
150
|
2,18
|
382,99
|
4,74
|
10
|
100
|
168,80
|
51,80
|
7,20
|
4,09
|
|
2
|
170
|
154
|
2,19
|
371,88
|
4,79
|
4
|
16
|
169,77
|
0,05
|
0,23
|
0,14
|
|
3
|
156
|
146
|
2,16
|
337,64
|
4,68
|
-10
|
100
|
167,81
|
139,56
|
-11,81
|
-7,57
|
|
4
|
172
|
134
|
2,13
|
365,86
|
4,52
|
6
|
36
|
164,67
|
53,67
|
7,33
|
4,26
|
|
5
|
162
|
132
|
2,12
|
343,53
|
4,50
|
-4
|
16
|
164,12
|
4,51
|
-2,12
|
-1,31
|
|
6
|
160
|
126
|
2,10
|
336,06
|
4,41
|
-6
|
36
|
162,42
|
5,86
|
-2,42
|
-1,51
|
|
7
|
166
|
133
|
2,12
|
352,56
|
4,51
|
0
|
0
|
164,40
|
2,56
|
1,60
|
0,96
|
|
Итого:
|
1162
|
975
|
15,00
|
2490,52
|
32,15
|
0
|
304
|
1162,00
|
258,012
|
0,00
|
-0,95
|
|
Средн.знач.
|
166,00
|
139,29
|
2,14
|
355,79
|
4,59
|
0,00
|
43,43
|
166,00
|
36,86
|
0,00
|
-0,14
|
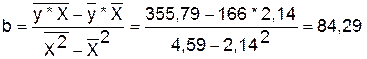
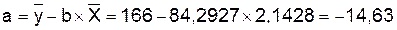
Уравнение будет иметь вид: 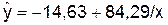
Произведем линеризацию модели путем
замены X=1/x
В результате получим линейное
уравнение 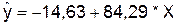
Определим индекс корреляции:
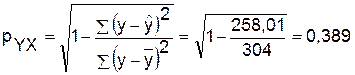
Связь между показателями y и фактором х можно считать умеренной.
Рассчитаем индекс детерминации:
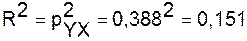
Вариация результата Y (объема выпуска продукции) на 15,1%
объясняется вариацией фактора Х (объем капиталовложений).
Оценку значимости уравнения регрессии
проведем с помощью F-критерия
Фишера:
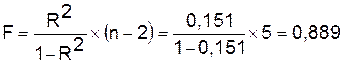
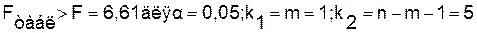
Следовательно, принимается гипотеза Hо
о статистически незначимых параметрах этого уравнения.
Этот результат можно объяснить
сравнительно невысокой теснотой выявленной зависимости и небольшим числом
наблюдений.
Определим среднюю относительную
ошибку:
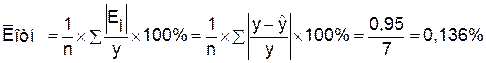
В среднем расчетные значения 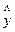 для линейной модели отличаются от фактических значений на
0,136%.
для линейной модели отличаются от фактических значений на
0,136%.
Найдем стандартную ошибку по формуле:
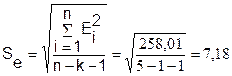
Для выбора лучшей модели построим сводную таблицу результатов
таблица 1.7
Таблица 1.7
|
Параметры
|
коэффициент
детерминации
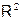
|
F-критерий
Фишера
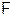
|
индекс корреляции
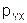
|
средняя относительная ошибка
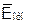
|
|
Модель
|
|
линейная
|
0,151
|
0,889
|
0,389
|
0,136
|
|
степенная
|
0,151
|
0,889
|
0,389
|
0,088
|
|
показательная
|
0,115
|
0,649
|
0,339
|
0,891
|
|
гиперболическая
|
0,151
|
0,889
|
0,389
|
0,136
|
В данном примере 3 модели имеют
одинаковые характеристики это линейная, степенная, гиперболическая модели, но
возьмем как лудшую одну, линейную модель для построения прогноза.
Рассчитаем прогнозное значение
результативного признака.
Прогнозное значение результативного
признака (объема выпуска продукции) определим по уравнению линейной модели,
подставив в него планируемую величину капиталовложений.
Прогнозное значение увеличится на 10 %
относительно среднего => 139,29*1,1=153,219
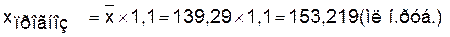
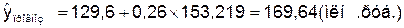
Ширина доверительного интервала
рассчитывается по формулам:
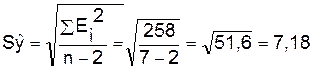
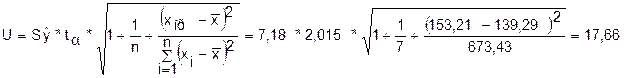
 Коэффициент Стьюдента ta для m = n -
2 = 5 и уровня значимости 0,1 равен 2,015.
Коэффициент Стьюдента ta для m = n -
2 = 5 и уровня значимости 0,1 равен 2,015.
 Таблица прогнозов (p = 90%)
Таблица прогнозов (p = 90%)
Таблица 1.8
|
Упреждение
|
Нижняя гр-ца
|
Прогноз
|
Верхняя гр-ца
|
|
1
|
151,98
|
169,64
|
187,30
|
Фактические, расчетные и прогнозные
значения по лучшей модели отобразим на графике.
Таблица 1.9
|
x
|
y
|
ŷ
|
|
150,00
|
176,00
|
168,8002
|
|
154,00
|
170,00
|
169,8456
|
|
146,00
|
156,00
|
167,7548
|
|
134,00
|
172,00
|
164,6186
|
|
132,00
|
162,00
|
164,0959
|
|
126,00
|
160,00
|
162,5278
|
|
133,00
|
166,00
|
164,3572
|
Линейная модель уравнения:
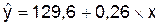
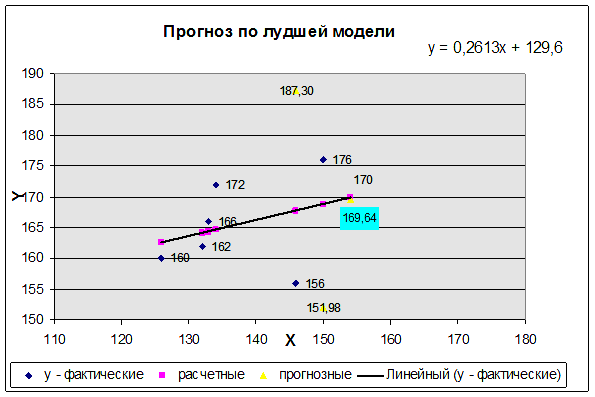
Рис.
1. Прогноз по лучшей модели
 Практическая
задача 2
Практическая
задача 2
2.1
Условие и исходные данные
По десяти кредитным учреждениям
получены данные, характеризующие зависимость объема прибыли (Y) от среднегодовой ставки по кредитам
(Х1), ставки по депозитам (Х2) и размера внутрибанковских
расходов (Х3).
Требуется:
1.
Осуществить выбор факторных признаков для построения двухфакторной
регрессионной модели.
2.
Рассчитать параметры модели.
3.
Для характеристики модели определить:
- линейный коэффициент множественной
корреляции;
- коэффициент детерминации;
- средние коэффициенты эластичности;
- бета-, дельта- коэффициенты.
Дать их интерпретацию.
4.
Осуществить оценку надежности уровня регрессии.
5.
Оценить с помощью t-критерия
Стьюдента статистическую значимость коэффициентов уравнения множественной
регрессии.
6.
Построить точечный и интервальный прогнозы результирующего показателя.
7. Отразить результаты расчетов на
графике
Выполнение задач отразить в
аналитической записке, приложить компьютерные распечатки расчетов.
Таблица
2.
|
Y
|
40
|
44
|
28
|
52
|
50
|
64
|
70
|
68
|
78
|
90
|
|
X1
|
32
|
40
|
44
|
28
|
50
|
56
|
50
|
56
|
60
|
62
|
|
X2
|
60
|
68
|
80
|
76
|
44
|
96
|
100
|
104
|
106
|
98
|
|
X3
|
50
|
54
|
60
|
62
|
70
|
54
|
84
|
82
|
86
|
84
|
2.2 Решение задачи
 1.Построение системы показателей
(факторов). Анализ матрицы коэффициентов парной корреляции. Выбор факторных
признаков для построения двухфакторной регрессионной модели.
1.Построение системы показателей
(факторов). Анализ матрицы коэффициентов парной корреляции. Выбор факторных
признаков для построения двухфакторной регрессионной модели.
Статистические данные по всем
переменным приведены в таблице 2.1. В нашем примере n=10, m=3.
Таблица 2.1
|
Y
|
X1
|
X2
|
X3
|
|
объем прибыли
|
ставка по кредитам
|
ставка по депозитам
|
внутрибанковские расходы
|
|
40
|
32
|
60
|
50
|
|
44
|
40
|
68
|
54
|
|
28
|
44
|
80
|
60
|
|
52
|
28
|
76
|
62
|
|
50
|
50
|
44
|
70
|
|
64
|
56
|
96
|
54
|
|
70
|
50
|
100
|
84
|
|
68
|
56
|
104
|
82
|
|
78
|
60
|
106
|
86
|
|
90
|
62
|
98
|
84
|
В таблице 2.2. приведены промежуточные
результаты при вычислении коэффициент корреляции по формуле:
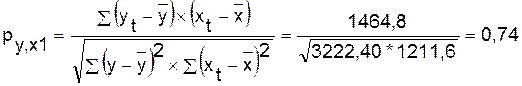
Таблица
2.2
|
t
|
Y
|
X1
|
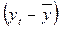
|
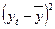
|
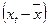
|
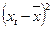
|
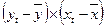
|
|
1
|
40
|
32
|
-18,4
|
338,56
|
-15,8
|
249,64
|
290,72
|
|
2
|
44
|
40
|
-14,4
|
207,36
|
-7,8
|
60,84
|
112,32
|
|
3
|
28
|
44
|
-30,4
|
924,16
|
-3,8
|
14,44
|
115,52
|
|
4
|
52
|
28
|
-6,4
|
40,96
|
-19,8
|
392,04
|
126,72
|
|
5
|
50
|
50
|
-8,4
|
70,56
|
2,2
|
4,84
|
-18,48
|
|
6
|
64
|
56
|
5,6
|
31,36
|
8,2
|
67,24
|
45,92
|
|
7
|
70
|
50
|
11,6
|
134,56
|
2,2
|
4,84
|
25,52
|
|
8
|
68
|
56
|
9,6
|
92,16
|
8,2
|
67,24
|
78,72
|
|
9
|
78
|
60
|
19,6
|
384,16
|
12,2
|
148,84
|
239,12
|
|
10
|
90
|
62
|
31,6
|
998,56
|
14,2
|
201,64
|
448,72
|
|
Итого
|
584
|
478
|
0
|
3222,40
|
0,00
|
1211,6
|
1464,8
|
|
Ср.знач.
|
58,4
|
47,8
|
0
|
322,24
|
0
|
121,16
|
146,48
|
 Используя инструмент корреляция
(анализ данных в Excel).
Получим следующие результаты:
Используя инструмент корреляция
(анализ данных в Excel).
Получим следующие результаты:
Результаты корреляционного анализа
Таблица 2.3
|
|
Объем прибыли Y
|
Cреднегодовая
ставка по кредиту X1
|
Ставка по депозиту
X2
|
Размер
внутрибанковских расходов X3
|
|
Объем прибыли Y
|
1
|
|
|
|
|
Cреднегодовая
ставка по кредиту X1
|
0,741
|
1
|
|
|
|
Ставка по депозиту
X2
|
0,697
|
0,616
|
1
|
|
|
Размер
внутрибанковских расходов X3
|
0,777
|
0,687
|
0,607
|
1
|
Анализ матрицы коэффициентов парной
корреляции показывает, что зависимая переменная, т.е. объем прибыли имеет
тесную связь с внутрибанковскими расходами (rYX3 = 0,77), с среднегодовыми ставками по
кредитам (rYX1 = 0,741). Однако факторы Х1 и Х3
тесно связаны между собой (rХ1X3 = 0,687), что свидетельствует
о наличии мультиколлинеарности. Из этих двух переменным оставим в модели Х3
- среднегодовые ставки по кредитам, переменная Х1
выбывает. Следовательно, после исключения
незначимых факторов n = 10, k = 2.
2.
Выбор вида модели и оценки ее параметров
Оценка
параметров регрессии осуществляется по методу наименьших квадратов по формуле 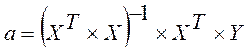
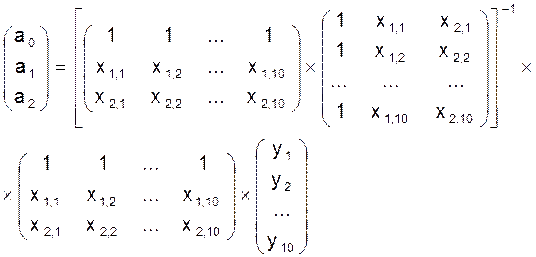
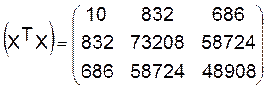
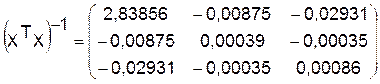
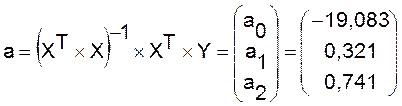
Уравнение регрессии зависимости объема
прибыли от ставки по депозитам и внутрибанковским расходам можно записать в
следующем виде:
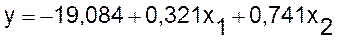
Расчетные значения Y определяются путем последовательной
подстановки в эту модель значений факторов, взятых для каждого наблюдения.
При помощи инструмента Регрессия
(Анализ данных в Excel),
получим результаты регрессионного анализа.
Таблица
2.4
|
Объем прибылиY
|
|
Ставка по депозиту
X2
|
Размер
внутрибанковских расходов X3
|
|
Y
|
X0
|
X1
|
X2
|
|
40
|
1
|
60
|
50
|
|
44
|
1
|
68
|
54
|
|
28
|
1
|
80
|
60
|
|
52
|
1
|
76
|
62
|
|
50
|
1
|
44
|
70
|
|
64
|
1
|
96
|
54
|
|
70
|
1
|
100
|
84
|
|
68
|
1
|
104
|
82
|
|
78
|
1
|
106
|
86
|
|
90
|
1
|
98
|
84
|
 Результат регрессионного анализа
содержится в таблицах 2.5-2.8. Рассмотрим содержание этих таблиц.
Результат регрессионного анализа
содержится в таблицах 2.5-2.8. Рассмотрим содержание этих таблиц.
Таблица
2.5
|
Регрессионная
статистика
|
|
|
Множественный
R
|
0,828
|
|
R-квадрат
|
0,685
|
|
Нормированный
R-квадрат
|
0,595
|
|
Стандартная
ошибка
|
12,05
|
|
Наблюдения
|
10
|
Дисперсионный анализ
Таблица
2.6
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
2
|
2206,758818
|
1103,379409
|
7,604709
|
0,017577738
|
|
Остаток
|
7
|
1015,641182
|
145,0915975
|
|
|
|
Итого
|
9
|
3222,4
|
|
|
|
Таблица 2.7
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
|
Y-пересечение
|
-19,08388188
|
20,29410859
|
-0,940365614
|
|
X1
|
0,320700684
|
0,240195807
|
1,33516354
|
|
X2
|
0,740547886
|
0,352707177
|
2,09961105
|
Вывод
остатка
Таблица 2.8
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
1
|
37,19
|
2,81
|
|
2
|
42,71
|
1,29
|
|
3
|
51,01
|
-23,01
|
|
4
|
51,20
|
0,80
|
|
5
|
46,87
|
3,13
|
|
6
|
51,69
|
12,31
|
|
7
|
75,19
|
-5,19
|
|
8
|
74,99
|
-6,99
|
|
9
|
78,60
|
-0,60
|
|
10
|
74,55
|
15,45
|
Уравнение регрессии зависимости объема
прибыли от ставки по депозитам и внутрибанковским расходам можно записать в
следующем виде:
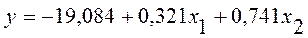
3.
Оценка качества модели
В таблице 2.8 приведены вычисленные по
модели значения Y
и значения остаточной компоненты.
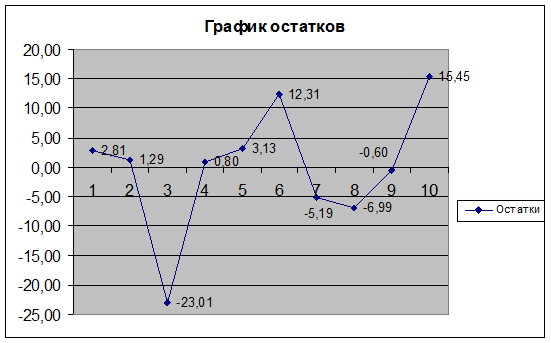
Рис.
2. График остатков
Проверку независимости проведем с
помощью d-критерия
Дарбина-Уотсона.
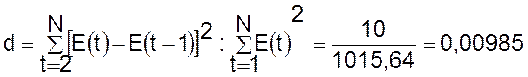
Зададим уровень значимости a=0,05. По таблицам значений критерия
Дарбина-Уотсона определим для числа наблюдений N=10 и числа независимых переменных
модели k=2
критические значения d1=0,70
d2=1,356. Получим
следующие промежутки внутри интервала (0;4)
0
4
|
|
d1=0,7
|
d2=1,64
|
4-d2=2,36
|
4-d1=3,3
|

Промежутки внутри интервала (0;4)
Фактически значение d=0,00985 попадает в промежуток от 0до d1. Следовательно есть положительная
автокорреляция остатков H0 отклоняется. С вероятностью P=(1-a) принимается H1, но нельзя сделать окончательный
вывод по этому критерию. Для определения степени автокорреляции вычислим
коэффициент автокорреляции и проверим его значимость при помощи стандартной
ошибки.
Стандартная ошибка коэффициента
корреляции рассчитывается следующим образом:
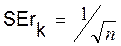

Коэффициент автокорреляции случайных
данных обладают выборочным распределением, приближающимся к нормальному с
нулевым математическим ожиданием средним квадратическим отклонением, равным 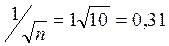 .
.
r1 не находится в интервале 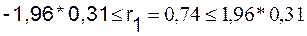 можно считать, что данные показывают наличие автокорреляции первого
порядка, т.к
можно считать, что данные показывают наличие автокорреляции первого
порядка, т.к 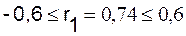 и свойство
независимости не выполняется.
и свойство
независимости не выполняется.
Вычислим для модели коэффициент
детерминации.
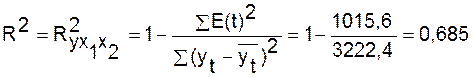
Он показывает долю
вариации результативного признака под воздействием изучаемых факторов x2 и x3. Около 68,5% вариации зависимой
переменной y учтено в
модели и обусловлено влиянием факторов x2 и x3.
Проверку значимости уравнения
регрессии произведем на основе вычисления F- критерия Фишера:
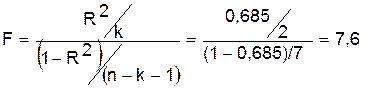
Табличное значение F-критерия при доверительной
вероятности 0,95 при k=2
и n-k-1=10-2-1=7 составляет 4,74.
Поскольку Fрас>Fтабл, уравнение регрессии следует признать
адекватным.
4. Оценить с помощью t - критерия Стьюдента статистическую
значимость коэффициентов уравнения множественной регрессии.
Значимость коэффициентов уравнения
регрессии a0,a1,a2 оценим с использованием t-критерия Стьюдента.
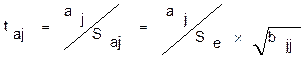
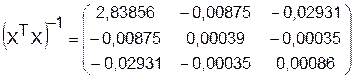
b11=2,83856
b22=0,00039
b33=0,00086
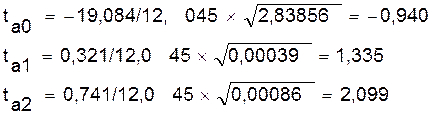
Табличное значение t-критерия при 5% уровне значимости и
степенях свободы (10-2-1=7) составляет 2,36. Так как 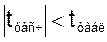 , то коэффициенты a1,a2 не существенны (не значимы).
, то коэффициенты a1,a2 не существенны (не значимы).
5. Проанализировать влияние факторов
на зависимую переменную по модели (для каждого коэффициента регрессии вычислить
коэффициент эластичности, 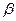 - коэффициент).
- коэффициент).
Коэффициент эластичности:
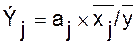
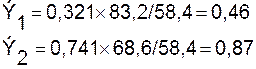
 Бета-коэффициент:
Бета-коэффициент:
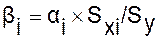
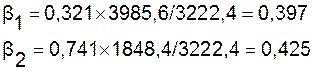
Таблица 2.9
|
Объем прибылиY
|
Ставка по
депозиту X1
|
Размер
внутрибанковских расходов X2
|
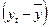
|
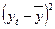
|
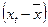
|
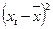
|
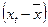
|
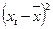
|
|
Y
|
X1
|
X2
|
|
|
X1
|
X1
|
X2
|
X2
|
|
40
|
60
|
50
|
-18,4
|
338,56
|
-23,20
|
538,24
|
-18,60
|
345,96
|
|
44
|
68
|
54
|
-14,4
|
207,36
|
-15,20
|
231,04
|
-14,60
|
213,16
|
|
28
|
80
|
60
|
-30,4
|
924,16
|
-3,20
|
10,24
|
-8,60
|
73,96
|
|
52
|
76
|
62
|
-6,4
|
40,96
|
-7,20
|
51,84
|
-6,60
|
43,56
|
|
50
|
44
|
70
|
-8,4
|
70,56
|
-39,20
|
1536,64
|
1,40
|
1,96
|
|
64
|
96
|
54
|
5,6
|
31,36
|
12,80
|
163,84
|
-14,60
|
213,16
|
|
70
|
100
|
84
|
11,6
|
134,56
|
16,80
|
282,24
|
15,40
|
237,16
|
|
68
|
104
|
82
|
9,6
|
92,16
|
20,80
|
432,64
|
13,40
|
179,56
|
|
78
|
106
|
86
|
19,6
|
384,16
|
22,80
|
519,84
|
17,40
|
302,76
|
|
90
|
98
|
84
|
31,6
|
998,56
|
14,80
|
219,04
|
15,40
|
237,16
|
|
584
|
832
|
686
|
0
|
3222,4
|
0,00
|
3985,6
|
0,00
|
1848,4
|
|
58,4
|
83,2
|
68,6
|
0
|
322,24
|
0,00
|
398,56
|
0,00
|
184,84
|
|
|
|
|
|
|
|
|
|
|
Коэффициент эластичности показывает,
на сколько % изменяется зависимая переменная при изменении фактора на 1%,т.е. при неизменном объеме внутрибанковских
расходов (x3) с увеличением среднегодовой ставки
по депозитам на 1% объем прибыли в среднем возрастет на 0,46% и с увеличением
внутрибанковских расходов на 1% объем прибыли возрастет на 0,87 %.
Средние показатели эластичности можно
сравнивать между собой и соответственно ранжировать факторы по силе их
воздействия на результат:
среднегодовая ставка по депозитам и
увеличение внутрибанковских расходов оказывает положительное воздействие на
объем прибыли, причём в данном случае можно сделать вывод о более сильном
влиянии на результат y
признака фактора x3, чем признака фактора x2: 0,46 % против 0,87 %.
Бета-коэффициент с математической
точки зрения показывает, на какую часть величины среднеквадратического
отклонения меняется среднее значение переменной с изменением независимой
переменной на одно среднеквадратическое отклонение при фиксированном на
постоянном уровне значениях независимых переменных. Это означает, что при
увеличении ставки по депозиту на 3985,6 тыс.руб. объем прибыли увеличится на
1279,29 тыс. руб. (0,397*3222,4).
При увеличении внутрибанковских
расходов на 1848,4 тыс.руб. объем прибыли увеличится на 1369,52 тыс.руб.
(0,425*3222,4)
 6.
Определить точечный и интервальный прогнозные оценки объема прибыли на два наблюдения
вперед.
6.
Определить точечный и интервальный прогнозные оценки объема прибыли на два наблюдения
вперед.
Прогнозные значения X1,11,X2,11
можно определить с помощью методов экспертных оценок, с помощью средних
абсолютных приростов или вычислить на основе экстраполяционных методов.
Если учесть что Хпр составляет 80% от
Х максимального
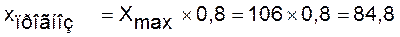
Для фактора X1 Ставка по депозиту выбрана модель:
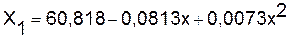
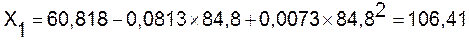
по которой получен прогноз на 1
наблюдения вперед.
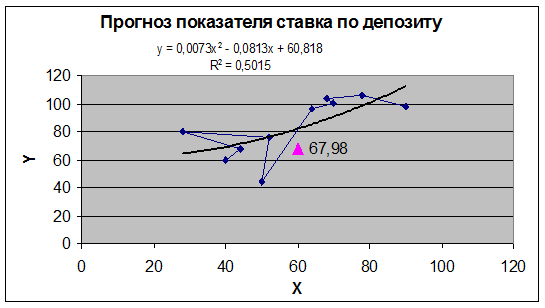
Рис. 3. Прогноз показателя Ставка по депозиту
Для фактора X2 размера внутрибанковских расходов
если учесть что Xпр
составляет 80% от X
максимального
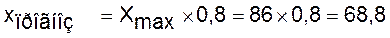
Для фактора X2 размера внутрибанковских расходов
выбрана модель:
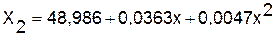
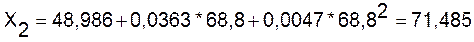
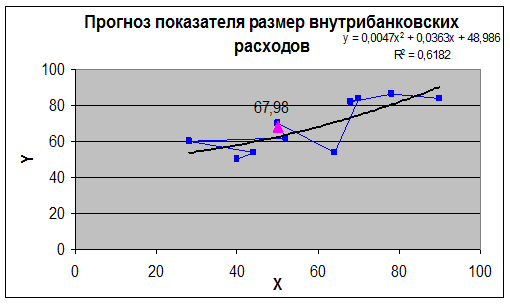
Рис. 4. Прогноз показателя Размер внутрибанковских расходов
Для получения прогнозных оценок
зависимостей переменной модели 
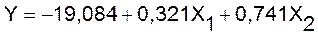
подставим в нее найденные прогнозные
значения факторов X
и X2.
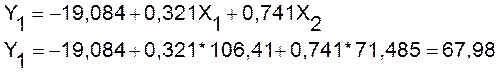
Доверительный интервал прогноза будет
иметь следующие границы:
Верхняя граница прогноза: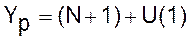
Нижняя граница прогноза: 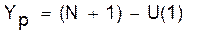
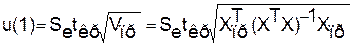
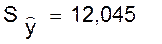
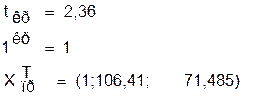
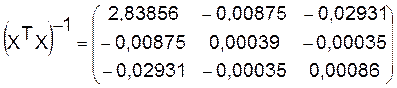
 u(1)=6,3
u(1)=6,3
Результаты прогнозных оценок
представим в таблице 2.10
Таблица
прогнозов (p=95%)
Таблица 2.10
|
Упреждение
|
Прогноз
|
Нижняя граница
|
Верхняя граница
|
|
1,00
|
67,98
|
61,68
|
74,28
|