ГОУ ВПО
ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО - ЭКОНОМИЧЕСКИЙ
ИНСТИТУТ КАФЕДРА ЭММиМ
Контрольная
работа по дисциплине
«Эконометрика»
Вариант
№ 4
Исполнитель: Маров
А.А.
Факультет:
Финансово-кредитный
Специальность:
Финансы и кредит
Группа: дневная,
2ВО
№ зачетной книжки
08ФФД62699
Руководитель:
Макаров Р.И.
Владимир
2009
Задача 1. Эконометрическое моделирование стоимости квартир в Московской области
Даны следующие исходные
данные:
|
Y - цена квартиры,
тыс. руб.
|
Х1 (город области)
|
Х2 (число комнат в
квартире)
|
Х4 (жилая площадь
квартиры)
|
|
40,5
|
1
|
1
|
19
|
|
64,7
|
1
|
2
|
36
|
|
127,5
|
0
|
3
|
41
|
|
63,6
|
1
|
2
|
34,8
|
|
69,5
|
0
|
1
|
18,7
|
|
95,5
|
0
|
2
|
27,7
|
|
120,5
|
1
|
3
|
59
|
|
134,5
|
0
|
3
|
44
|
|
95
|
0
|
3
|
56
|
|
107,5
|
1
|
4
|
47
|
|
44,5
|
1
|
1
|
18
|
|
127,5
|
1
|
3
|
44
|
|
172,5
|
0
|
4
|
56
|
|
40,5
|
0
|
1
|
16
|
|
133
|
0
|
4
|
66
|
|
87,5
|
0
|
2
|
34
|
|
100,5
|
0
|
4
|
43
|
|
130,5
|
0
|
4
|
59,2
|
|
87,5
|
0
|
3
|
50
|
|
162,5
|
1
|
3
|
42
|
|
62,5
|
0
|
1
|
20
|
|
43,5
|
1
|
1
|
14
|
|
92,5
|
1
|
4
|
47
|
|
85,5
|
0
|
4
|
49,5
|
|
47,5
|
0
|
1
|
18,9
|
|
41,5
|
0
|
1
|
18
|
|
89,4
|
0
|
3
|
58,7
|
|
42,5
|
0
|
1
|
22
|
|
82,5
|
0
|
2
|
40
|
|
229,5
|
0
|
4
|
91
|
|
237,5
|
0
|
4
|
90
|
|
42,5
|
1
|
1
|
15
|
|
69,5
|
1
|
1
|
18,5
|
|
125,5
|
1
|
4
|
55
|
|
102,5
|
0
|
3
|
37
|
|
107,5
|
1
|
3
|
48
|
|
72,8
|
1
|
2
|
34,8
|
|
84,5
|
1
|
3
|
48
|
|
282,5
|
1
|
4
|
85
|
|
202,5
|
1
|
4
|
60
|
1. Рассчитать
матрицу парных коэффициентов корреляции; оценить статистическую значимость
коэффициентов корреляции.
2. Построить поле
корреляции результативного признака и наиболее тесно связанного с ним фактора.
3. Рассчитать
параметры линейной парной регрессии для каждого фактора Х.
4. Оценить
качество каждой модели через коэффициент детерминации, среднюю ошибку
аппроксимации и F-критерий Фишера. Выбрать лучшую модель.
5. Для выбранной
модели осуществить прогнозирование среднего значения показателя Y при уровне значимости α = 0,05,
если прогнозное значение фактора Y составит 80% от его максимального значения. Представить
графически: фактические и модельные значения, точки прогноза.
6. Используя
пошаговую множественную регрессию ( метод исключения или метод включения),
построить модель формирования цены
квартиры за счет значимых факторов. Дать экономическую интерпретацию
коэффициентов модели регрессии.
7. Оценить
качество построенной модели. Улучшилось ли качество модели по сравнению с
однофакторной моделью? Дать оценку влияния значимых факторов на результат с
помощью коэффициентов эластичности, β- и Δ – коэффициентов.
Решение:
При решении данной
задачи расчеты и построение графиков и диаграмм будем вести с использованием
настройки Excel Анализ
данных и программы SPSS.
1. Рассчитаем
матрицу парных коэффициентов корреляции и оценим значимость коэффициентов
корреляции.
Чтобы рассчитать
матрицу парных коэффициентов корреляции скопируем таблицу с исходными данными в
Excel. Далее
воспользуемся инструментом Корреляция, входящим в настройку Анализ данных.
В диалоговом окне
Корреляция в поле Входной интервал вводим диапазон ячеек, содержащих исходные
данные. Так как мы выделили и заголовки столбцов, то устанавливаем флажок Метки
в первой строке.
Получили следующие
результаты:
Таблица 1.1.
Матрица парных коэффициентов
корреляции
|
|
Y - цена квартиры,
тыс. руб.
|
Х1 (город области)
|
Х2 (число комнат в
квартире)
|
Х4 (жилая площадь
квартиры)
|
|
Y - цена квартиры, тыс. руб.
|
1
|
-0,01126
|
0,751061
|
0,874012
|
|
Х1 (город области)
|
-0,01126
|
1
|
-0,0341
|
-0,0798
|
|
Х2 (число комнат в квартире)
|
0,751061
|
-0,0341
|
1
|
0,868524
|
|
Х4 (жилая площадь квартиры)
|
0,874012
|
-0,0798
|
0,868524
|
1
|
Анализ матрицы коэффициентов парной корреляции показывает,
что зависимая переменная Y , т.е. цена квартиры имеет более тесную связь с Х4 (жилая площадь
квартиры). Коэффициент корреляции равен 0,874. Это означает, что на 87,4
зависимая переменная Y (цена квартиры) зависит от показателя Х4 (жилая площадь
квартиры). Также зависимая переменная Y (цена квартиры) имеет среднюю связь
с Х2 (число комнат в квартире) и слабую связь с Х1 (город области). В то же время межфакторная связь между Х2
(число комнат в квартире) и Х4 (жилая площадь квартиры) равна 0,869 весьма
тесная, что свидетельствует о наличии мультиколлинеарности. Факторы Х2 и Х4
связаны между собой линейной зависимостью, т.е. имеет место совокупное
воздействие факторов друг на друга. Вследствие этого вариация в исходных данных
перестает быть полностью независимой, и нельзя оценить воздействие каждого
фактора в отдельности.
Статистическую значимость
коэффициентов корреляции определим
помощью t-критерия Стьюдента. Табличное значение сравниваем с расчетными
значениями.
Вычислим табличное
значение с помощью функции СТЬЮДРАСПОБР.
Tтабл.=
2,0244 при доверительной вероятности 0,05 и степенью свободы (n-2).
Статистическим
значимым является фактор Х4.
2. Построим поле
корреляции результативного признака (стоимости квартиры) и наиболее тесно связанного с ним фактора
(жилой площади квартиры).
Для этого воспользуемся инструментом построения точечной
диаграммы программы Excel.
В результате
получаем поле корреляции цены квартиры, тыс. долларов и жилой площади квартиры,
кв. м. (рисунок 1.1)
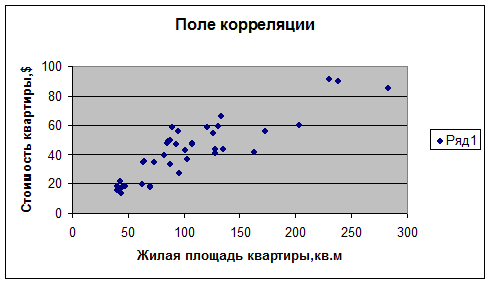
Рисунок 1.1.
3. Рассчитаем параметры
линейной парной регрессии для каждого фактора Х.
Для расчета
параметров линейной парной регрессии воспользуемся инструментом Регрессия,
входящим в настройку Анализ данных.
В диалоговом окне
Регрессия в поле Входной интервал Y вводим адрес диапазона
ячеек, которые представляют зависимую переменную, т.е стоимость квартир. В поле
Входной интервал Х вводим адрес диапазона, который содержит значения зависимых
переменных (горд области, жилая площадь квартиры, число комнат в квартире).
Выполним поочередно вычисления параметров парной регрессии для каждого фактора
Х.
Для Х4 получили следующие данные, представленные в таблице
1.2:
Таблица 1.2
|
|
Коэффициенты
|
|
Y - пересечение
|
-0,36485
|
|
Х4 - жилая площадь квартиры, кв.м
|
2,475975
|
Уравнение регрессии
зависимости цены квартиры от жилой площади квартиры имеет вид:
Y4 = 10,04+0,3085* Х4
Для Х2 получили
следующие данные, представленные в таблице 1.3:
Таблица 1.3
|
|
Коэффициенты
|
|
Y - пересечение
|
10,0393
|
|
Х2 - число комнат в квартире
|
36,03777
|
Уравнение
регрессии зависимости цены квартиры от числа комнат в квартире имеет вид:
Y2 = 0,9762+0,0157* Х2
Для Х1 получили
следующие данные, представленные в таблице 1.4:
Таблица 1.4
|
|
Коэффициенты
|
|
Y - пересечение
|
104,3136
|
|
Х1 -город области
|
-1,2803
|
Уравнение регрессии зависимости цены квартиры
от города области имеет вид:
Y1
= 0,4603+1E-04x* Х1
4.
Оценим качество каждой модели через коэффициент детерминации, среднюю
ошибку аппроксимации и F-критерий Фишера. Установим, какая модель является лучшей.
Коэффициент детерминации, среднюю ошибку аппроксимации мы
получили в результате расчетов, проведенных в пункте 3. Полученные данные
представлены в следующих таблицах:
Данные по Х4:
Таблица 1.5 а
|
Регрессионная статистика
|
|
Множественный R
|
0,874012079
|
|
R-квадрат
|
0,763897114
|
|
Нормированный R-квадрат
|
0,75768388
|
|
Стандартная ошибка
|
28,20194696
|
|
Наблюдения
|
40
|
Таблица 1.5 б
|
Дисперсионный
анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
97785,70089
|
97785,70089
|
122,9467832
|
1,79185E-13
|
|
Остаток
|
38
|
30223,29286
|
795,3498121
|
|
|
|
Итого
|
39
|
128008,9938
|
|
|
|
Данные по Х2:
Таблица 1.6 а
|
Регрессионная
статистика
|
|
Множественный R
|
0,75106074
|
|
R-квадрат
|
0,564092234
|
|
Нормированный R-квадрат
|
0,552620977
|
|
Стандартная ошибка
|
38,32002171
|
|
Наблюдения
|
40
|
Таблица 1.6 б
|
Дисперсионный
анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
72208,87932
|
72208,87932
|
49,17440478
|
2,36579E-08
|
|
Остаток
|
38
|
55800,11443
|
1468,424064
|
|
|
|
Итого
|
39
|
128008,9938
|
|
|
|
Данные по Х1:
Таблица 1.7 а
|
Регрессионная
статистика
|
|
Множественный R
|
0,011259267
|
|
R-квадрат
|
0,000126771
|
|
Нормированный R-квадрат
|
-0,026185682
|
|
Стандартная ошибка
|
58,03645994
|
|
Наблюдения
|
40
|
Таблица 1.7 б
|
Дисперсионный
анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
16,22784091
|
16,22784091
|
0,004817913
|
0,945026312
|
|
Остаток
|
38
|
127992,7659
|
3368,230682
|
|
|
|
Итого
|
39
|
128008,9938
|
|
|
|
А) Коэффициент детерминации определяет, какая
доля вариации признака Y учтена в модели и обусловлена влиянием не него фактора Х.
Чем больше значение коэффициента детерминации, тем теснее связь между
признаками в построенной математической модели.
В программе Excel обозначается R-квадрат:
Rх42 = 0,764
Rх22 = 0,564
Rх12 = 0,0001
Исходя из данного
критерия наиболее адекватной является модель уравнения регрессии зависимости
цены квартиры от жилой площади квартиры (Х4).
Б) Среднюю ошибку аппроксимации рассчитываем по
формуле:
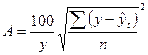, где числитель – сумма квадратов отклонения расчетных
значений от фактических. В таблицах она находится в столбце SS, строке Остатки.
Среднее значение
цены квартиры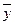 
рассчитаем в Excel с помощью функции СРЗНАЧ. 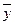= 103,7375 тыс. долл.
При проведении
экономических расчетов модель считается достаточно точной, если средняя ошибка
аппроксимации меньше 5%, модель считается приемлемой, если средняя ошибка
аппроксимации меньше 15%.
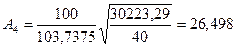
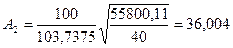
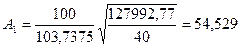
По данному критерию,
наиболее адекватной является математическая модель для уравнения регрессии
зависимости цены квартиры от жилой площади квартиры (Х4).
В) Для проверки значимости модели регрессии
используется F-тест. Для этого выполняется сравнение Fфакт. И и критического (табличного) Fтабл. Значений критерия Фишера.
Расчетные значения
приведены в таблицах 1.5 б, 1.6 б, 1.7 б
(обозначены буквой F).
Табличное значение
F-критерий Фишера
рассчитываем в Excel с помощью функции FРАСПОБР. Вероятность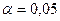 
, число степеней
свободы: f1 =2,
f2 =10.
Получили: Fтабл. = 4,10
Расчетные
значения критерий Фишера для каждого фактора сравним с табличным значением:
Fх4 = 122,94> Fтабл. = 4,10 модель по данному критерию адекватна.
Fх2 = 49,17> Fтабл. = 4,10 модель по данному критерию адекватна.
Fх1 = 0,0048> Fтабл. = 4,10 модель по данному критерию не адекватна.
Проанализировав
данные по всем трем критериям, можно сделать вывод, что наиболее лучшей
является математическая модель, построенная для фактора жилая площадь квартиры,
которая описана уравнением Y4 = 10,04+0,3085* Х4
5. Для
выбранной модели зависимости цены квартиры от жилой площади квартиры Y = 10,04+0,3085* Х осуществим
прогнозирование среднего значения показателя Y при уровне значимости
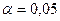, если прогнозное значение
фактора Х составит
80% от его максимального значения.
Рассчитаем прогнозное значение Х, по условию оно составит 80% от
максимального значения.
Рассчитаем Хmax
в Excel с помощью функции МАКС.
Хmax = 91 кв.м
Х41 =
0,8 * 91 = 72,8 кв.м
Для получения
прогнозных оценок зависимой переменной подставим полученное значение независимой
переменной в линейное уравнение:
Y41 = 10,04+0,3085* 72,8 = 32,4988 тыс.долл.
Определим
доверительный интервал прогноза, который будет иметь следующие границы:
yp
(N + l) + U(l)
yp (N + l) – U(l)
Для вычисления
доверительного интервала для прогнозного значения, рассчитываем величину отклонения от линии
регрессии. Для модели парной регрессии величина отклонения рассчитывается:
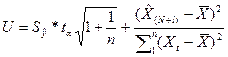В результате получаем поле корреляции цены
квартиры, тыс. ммы программы мой, и нельзя оценить воз Табли
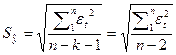, т.е.
значение стандартной ошибки из таблицы 1.5 а.
(Так как число
степеней свободы равно единице, то знаменатель будет равен n-2).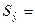 
28,20
Для расчета
коэффициента 
воспользуемся функцией Excel
СТЬЮДРАСПОБР, вероятность α
= 0,05, число степеней свободы: (n-2) = 40 -2 = 38. =
2.0244
Значение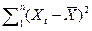 
рассчитаем с помощью Excel, получили 15950,82
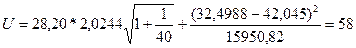
Определим верхнюю и нижнюю границы интервала:
32,4988 + 58 =
90,4988
32,4988 - 58 =
-25,5012
Таким образом,
прогнозное значение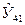 
= 32,4988 тыс.долл., будет находиться между нижней границей,
равной -25,5012 тыс.долл. и верхней
границей, равной 90,4988тыс.долл.
Фактические и
модельные значения, точки прогноза представлены графически на рисунке 1.2.
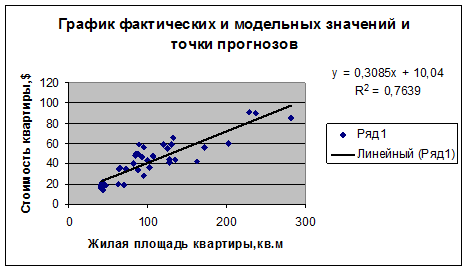
Рисунок 1.2
6. Используя пошаговую множественную
регрессию (метод исключения), построим модель формирования цены квартиры за
счет значимых факторов.
Коэффициент парной корреляции независимых переменных Х2 (число комнат в
квартире) и Х4 (жилая площадь квартиры) rx2x4 = 0,868524. Так как это больше 0,8,
следовательно, в исходных данных имеется мультиколлинеарность. Чтобы избавиться
от мультиколлинеарности из переменных Х2 (число комнат в квартире) и Х4 (жилая
площадь квартиры) оставим в модели Х4, так как он в большей степени связан с
зависимой переменной Y (цена квартиры).
Для построения множественной регрессии воспользуемся функцией Регрессия
программы Excel, включив в нее факторы: Y, X1, X4. В результате получаем результативные таблицы, из
которых нам необходим t-критерий Стьюдента.
Таблица 1.8.а
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
|
Y-пересечение
|
-3,9361
|
11,51649
|
-0,34178
|
0,73445
|
|
Х1 (город области)
|
6,692936
|
9,045869
|
0,739889
|
0,464037
|
|
Х4 (жилая площадь квартиры)
|
2,48928
|
0,22536
|
11,04581
|
2,85E-13
|
Таблица 1.8.б
|
Регрессионная
статистика
|
|
Множественный R
|
0,875979141
|
|
R-квадрат
|
0,767339455
|
|
Нормированный R-квадрат
|
0,754763209
|
|
Стандартная ошибка
|
28,37139894
|
|
Наблюдения
|
40
|
Таблица 1.8.в
|
Дисперсионный анализ
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
2
|
98226,35
|
49113,18
|
61,01499
|
1,92E-12
|
|
Остаток
|
37
|
29782,64
|
804,9363
|
|
|
|
Итого
|
39
|
128009
|
|
|
|
Получаем модель
вида:
Y =2,48928Х4 +6,692936Х1
-3,9361. Поскольку Fтабл. < Fрасч. (4,10 < 61,01), уравнение регрессии следует признать адекватным.
Выберем наименьшее
по модулю значение –критерия Стьюдента, оно равно | 0,73|,
сравним его с табличным значением, которое рассчитаем в Excel, уровень значимости берем 0,05,
число степеней свободы n – m -1 = 40 – 3 : t табл. = 2,026.
Поскольку
| 0,73| < 2,026 модель следует
признать не адекватной.
7.
Оценка качества построенной модели.
а) Для модели Y = 2,48928Х4 +6,692936Х1
-3,9361 коэффициент детерминации составил
0,77, для модели Y4 = 10,04+0,3085* Х4 он составил 0,76
поскольку чем больше значение коэффициента детерминации, тем теснее связь между
признаками в построенной математической модели, то первая модель является
лучшей по данному критерию.
б) Рассчитаем среднюю ошибку аппроксимации:
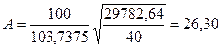
Для
предыдущей модели она составила 26,498.
в) Рассчитаем табличное значение F-критерия Фишера при вероятности 0,05,
число
степеней свободы: f1 =2,
f2 =10:
Fтабл. = 4,10
Fфакт. = 61,01
Fфакт. = 61,01> Fтабл. = 4,10 - модель по данному критерию адекватна.
Для оценки
значимого фактора полученной математической модели, рассчитаем коэффициенты эластичност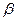и, 
и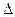 
- коэффициенты.
Коэффициент
эластичности показывает, на сколько процентов изменится результативный признак
при изменении факторного признака на 1%.
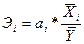
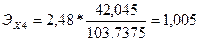
То есть с
ростом жилой площади квартиры на 1%
стоимость квартиры возрастает в среднем на 1%.
Наибольшее
воздействие на цену квартиры оказывает величина жилой площади (Х4). 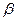- коэффициент
показывает, на какую часть величины среднего квадратического отклонения
меняется среднее значение зависимой переменной с изменением независимой
переменной на одно среднеквадратическое отклонение.
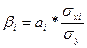
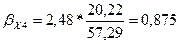
Данные средних квадратических отклонений
взяты из таблиц, полученных с помощью инструмента Описательная статистика.
Таблица 1.10
Таблица
1.11
Описательная статистика
(Х4). Описательная
статистика (Y).
|
Среднее
|
42,045
|
|
|
Среднее
|
103,7375
|
|
Стандартная
ошибка
|
3,197637249
|
|
|
Стандартная
ошибка
|
9,058534499
|
|
Медиана
|
42,5
|
|
|
Медиана
|
90,95
|
|
Мода
|
34,8
|
|
|
Мода
|
40,5
|
|
Стандартное
отклонение
|
20,22363367
|
|
|
Стандартное
отклонение
|
57,29120256
|
|
Дисперсия
выборки
|
408,995359
|
|
|
Дисперсия
выборки
|
3282,281891
|
|
Эксцесс
|
0,176467768
|
|
|
Эксцесс
|
1,881361071
|
|
Асимметричность
|
0,616950353
|
|
|
Асимметричность
|
1,370739008
|
|
Интервал
|
77
|
|
|
Интервал
|
242
|
|
Минимум
|
14
|
|
|
Минимум
|
40,5
|
|
Максимум
|
91
|
|
|
Максимум
|
282,5
|
|
Сумма
|
1681,8
|
|
|
Сумма
|
4149,5
|
|
Счет
|
40
|
|
|
Счет
|
40
|
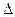- коэффициент
определяет долю влияния фактора в суммарном влиянии всех факторов:
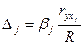
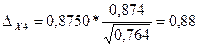
ВЫВОД:
Из полученных
расчетов можно сделать вывод, что результативный признак Y (цена квартиры) на 84% зависит от фактора Х4 (жилая площадь
квартиры).
Задача 2. Исследовать динамику экономического показателя на основе
анализа одномерного временного ряда.
В течение девяти
последовательных недель фиксировался спрос Y(t) .руб.) на кредитные ресурсы
финансовой компании. Временной ряд этого показателя приведен ниже в таблице
|
Номер наблюдения
(t = 1,2,…..,9)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
32,5
|
30,5
|
35,5
|
39,5
|
42,5
|
44,5
|
46,5
|
51,5
|
49,5
|
Требуется:
1) Проверить
наличие аномальных наблюдений.
2) Построить
линейную модель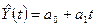 
, параметры которой оценить
МНК
(
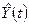
- расчетные, смоделированные значения временного ряда).
3) Оценить
адекватность построенных моделей, используя свойства независимости остаточной
компоненты, случайности и соответствия нормальному закону распределения (при
использовании R/S – критерия взять табулированные 2,7 – 3,7).
4) Оценить
точность моделей на основе использования средней относительной ошибки
аппроксимации.
5) Осуществить
прогноз спроса на следующие две недели (доверительный интервал прогноза
рассчитать при доверительной вероятности
р = 70%).
6) Фактические
значения показателя, результаты моделирования и прогнозирования представить
графически.
Решение:
1) Проверим наличие аномальных наблюдений
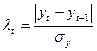
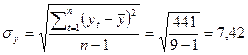
Результаты
расчетов приведены в таблице 2.1.
Таблица
2.1
|
t
|
y
|
|
|
|
|
|
|
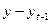
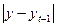
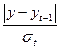
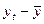
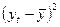
1
|
32,5
|
|
|
|
-8,88889
|
79,01237
|
|
2
|
30,5
|
-2
|
2
|
0,269542
|
-10,8889
|
118,5679
|
|
3
|
35,5
|
5
|
5
|
0,673854
|
-5,88889
|
34,67903
|
|
4
|
39,5
|
4
|
4
|
0,539084
|
-1,88889
|
3,567905
|
|
5
|
42,5
|
3
|
3
|
0,404313
|
1,11111
|
1,234565
|
|
6
|
44,5
|
2
|
2
|
0,269542
|
3,11111
|
9,679005
|
|
7
|
46,5
|
2
|
2
|
0,269542
|
5,11111
|
26,12345
|
|
8
|
51,5
|
5
|
5
|
0,673854
|
10,11111
|
102,2345
|
|
9
|
49,5
|
-2
|
2
|
0,269542
|
8,11111
|
65,79011
|
|
Сумма
|
372,5
|
|
|
|
|
440,8889
|
Сравним расчетное
значение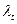 
с табличным значением
(
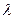табл.= 1,5).
Все расчетные значения 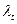меньше 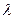табл., следовательно, аномальных значений во
временном ряду нет.
2)
Построим линейную модель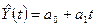
Рассчитаем коэффициенты линейной модели с помощью инструмента
Регрессия программы Excel. В качестве входного
интервала Y берем
значения спроса на кредитные ресурсы финансовой компании, в качестве входного
интервала Х – номера наблюдений.
Результаты
приведены в таблицах:
Таблица 2.2а
|
Регрессионная
статистика
|
|
Множественный R
|
0,971442019
|
|
R-квадрат
|
0,943699597
|
|
Нормированный R-квадрат
|
0,935656682
|
|
Стандартная ошибка
|
1,883091008
|
|
Наблюдения
|
9
|
Таблица
2.2б
|
Дисперсионный
анализ
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
Регрессия
|
1
|
416,0666667
|
416,0666667
|
117,3330349
|
1,26027E-05
|
|
Остаток
|
7
|
24,82222222
|
3,546031746
|
|
|
|
Итого
|
8
|
440,8888889
|
|
|
|
Таблица 2.2в
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
|
Y-пересечение
|
28,22222222
|
1,368033901
|
20,62976816
|
1,57859E-07
|
|
Переменная X 1
|
2,633333333
|
0,243106004
|
10,83203743
|
1,26027E-05
|
Таблица 2.2г
|
ВЫВОД ОСТАТКА
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
|
1
|
30,85555556
|
1,644444444
|
|
2
|
33,48888889
|
-2,988888889
|
|
3
|
36,12222222
|
-0,622222222
|
|
4
|
38,75555556
|
0,744444444
|
|
5
|
41,38888889
|
1,111111111
|
|
6
|
44,02222222
|
0,477777778
|
|
7
|
46,65555556
|
-0,155555556
|
|
8
|
49,28888889
|
2,211111111
|
|
9
|
51,92222222
|
-2,422222222
|
Уравнение линейной
модели будет иметь вид:
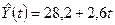
3) Оценим
адекватность построенных моделей, используя свойства независимости остаточной
компоненты, случайности и соответствия нормальному закону распределения.
Модель является
адекватной, если математическое ожидание значений остаточного ряда близко или
равно нулю, и если значения остаточного ряда случайны, независимы и подчинены
нормальному закону распределения.
а) При проверке
независимости ( отсутствие автокорреляции) определяется отсутствие в ряду
остатков систематической составляющей
(с помощью d – критерия Дарбина-Уотсона).
Таблица 2.3
Таблица для вычисления d-критерия
|
Наблюдение
|
Y расчетное
|
Отклонение
Е(t)
|
Е(t) – Е(t-1)
|
(E(t) – E(t-1))2
|
E(t)2
|
|
1
|
30,85555556
|
1,644444444
|
|
|
2,704198
|
|
2
|
1,644444444
|
-2,988888889
|
-4,63333
|
21,46777778
|
8,933457
|
|
3
|
-2,988888889
|
-0,622222222
|
2,366667
|
5,601111111
|
0,38716
|
|
4
|
-0,622222222
|
0,744444444
|
1,366667
|
1,867777778
|
0,554198
|
|
5
|
0,744444444
|
1,111111111
|
0,366667
|
0,134444444
|
1,234568
|
|
6
|
1,111111111
|
0,477777778
|
-0,63333
|
0,401111111
|
0,228272
|
|
7
|
0,477777778
|
-0,155555556
|
-0,63333
|
0,401111111
|
0,024198
|
|
8
|
-0,155555556
|
2,211111111
|
2,366667
|
5,601111111
|
4,889012
|
|
9
|
2,211111111
|
-2,422222222
|
-4,63333
|
21,46777778
|
5,86716
|
|
СУММА
|
|
|
|
56,94222222
|
24,82222
|
(Значения остатков взяты из таблицы 2.2г).
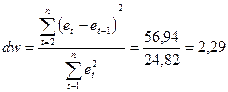
Зададим уровень
значимости равной 0,05. По таблицам значений критерия Дарбина-Уотсона для числа n = 9 и числа независимых переменных
модели
k = 1 критическое значение d1 = 0,82 и d2 = 1,32
Так как d попало в интервал от 2 до 4, то
вычисляем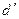 
:
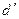= 4 – 2,29 = 1,71
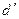попало в
интервал: d2 = 1,3 < d = 1,71 < 2 , по данному критерию модель адекватна.
б) Проверку случайности
уровней ряда остатков проведем на основе критерия поворотных точек.
В случайном ряду
чисел должно выполняться строгое неравенство:
p >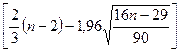 
p > =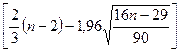
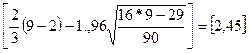
Количество поворотных точек равно 5 (рисунок 2.1). Первая
часть неравенства равна 2,45. Неравенство выполняется: 5 > 2, следовательно,
свойство случайности выполняется.
Модель по этому критерию адекватна.
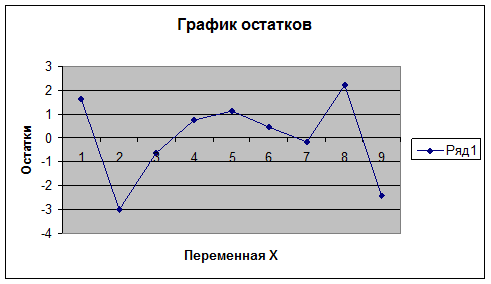
Рисунок 2.1
в) Соответствие ряда остатков нормальному закону
распределения определим при помощи RS-критерия.
RS
= [ Emax - Emin] / SE
Emax – максимальный уровень ряда остатков
= 2,21
Emin – минимальный уровень ряда остатков
= -2,99
SE - среднее квадратичное отклонение
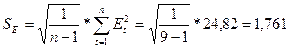
RS = [2,21– (-2,99)] / 1,761 = 2,953
Расчетное значение
попадает в интервал (2,7 – 3,7), следовательно, свойство нормальности
распределения выполняется. Модель по
этому критерию адекватна.
4) Оценим точность модели на основе
использования средней относительной ошибки аппроксимации.
Среднюю
относительную ошибку аппроксимации рассчитаем по формуле:
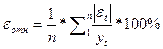
Построим расчетную
таблицу:
Таблица 2.4
|
t
|
y
|
E(t)
|
|E(t)|
|
|
|
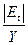
1
|
32,5
|
1,6444444
|
1,6444444
|
0,050598
|
|
2
|
30,5
|
-2,9888889
|
2,9888889
|
0,097996
|
|
3
|
35,5
|
-0,6222222
|
0,6222222
|
0,017527
|
|
4
|
39,5
|
0,7444444
|
0,7444444
|
0,018847
|
|
5
|
42,5
|
1,1111111
|
1,1111111
|
0,026144
|
|
6
|
44,5
|
0,4777778
|
0,4777778
|
0,010737
|
|
7
|
46,5
|
-0,1555556
|
0,1555556
|
0,003345
|
|
8
|
51,5
|
2,2111111
|
2,2111111
|
0,042934
|
|
9
|
49,5
|
-2,4222222
|
2,4222222
|
0,048934
|
|
Итого
|
|
|
|
0,317062
|
Данную модель
можно считать приемлемой, так как рассчитанное значение средней относительной
ошибки аппроксимации меньше 15%.
3,5% - хороший уровень точности модели.
5)
Осуществим прогноз спроса на следующие две недели.
Рассчитаем
прогнозные значения для 10 и 11 недели, подставив соответствующие значения в
ранее полученное уравнение регрессии:
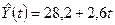
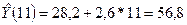
Доверительные интервалы для прогнозных значений рассчитываем по формуле:
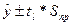, где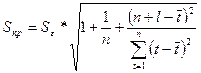 
Среднее значение
параметра t равно:
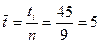
Рассчитаем
знаменатель дроби, находящейся под корнем, для этого построим расчетную
таблицу:
Таблица 2.5
|
t
|
|
|
|
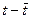
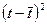
1
|
-4
|
16
|
|
2
|
-3
|
9
|
|
3
|
-2
|
4
|
|
4
|
-1
|
1
|
|
5
|
0
|
0
|
|
6
|
1
|
1
|
|
7
|
2
|
4
|
|
8
|
3
|
9
|
|
9
|
4
|
16
|
|
Итого
|
|
60
|
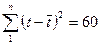
Из таблицы 2.2а берем значение
стандартной ошибки оценки:
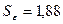
Рассчитаем Sпр для каждой недели:
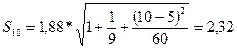
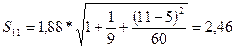
Рассчитаем t-критерий Стьюдента с помощью формулы
СТЬЮДРАСПОБР, при доверительной вероятности равной 70%, α =0,3, число
степеней свободы n =2:
t = 1,386
Рассчитаем
доверительные интервалы:
Для 10-й недели:
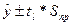
54,2+1,386*2,32 =57,41
54,2-1,386*2,32 =
50,98
Для 11-й недели:
56,8+1,386*2,46 = 60,21
56,8-1,386*2,46 = 53,39
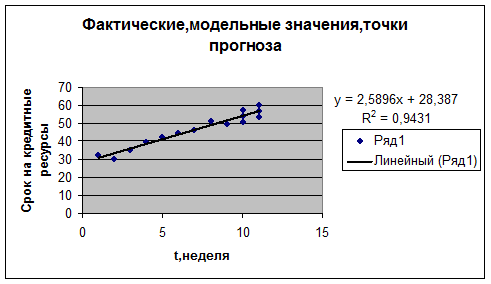
6)
Представим графически фактические значения показателя, результаты
моделирования и прогнозирования.
Список литературы:
1.
Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: Учеб. Пособие. – М.: Вузовский учебник, 2007.
2.
Орлова И.В. Экономико-математические методы и модели. Выполнение
расчетов в среде EXCEL: Практикум: Учеб. Пособие
для вузов. – М.: Финстатинформ, 2000.
3.
Эконометрика: Учебник / Под редакцией И,И, Елисеевой. – М.: Финансы и
статистика, 2002.
4.
Практикум по эконометрике: Учебное пособие / Под ред. И.И. Елисеевой. –
М.: Финансы и статистика, 2001.
5.
Экономико-математические методы и прикладные модели: Учеб. Пособие для
вузов / В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов, И.В. Орлова, В.А.
Половников. – М.: ЮНИТИ, 1999.
6.
Гусаров В.М. Статистика: Учеб.
Пособие для вузов. – М.: ЮНИТИ-ДАНА, 2001.
7.
Эконометрика. Методические указания. – М.: Вузовский учебник, 2005.
8.
Эконометрика. Методические указания. – М.: ИНФРА-М; Вузовский учебник,
2007.