ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ
ИНСТИТУТ
Контрольная работа
по дисциплине
«ЭКОНОМЕТРИКА»
Вариант № 2
Выполнила:
Студентка 3 курса:
Факультет: финансово-кредитный
Специальность: финансы и кредит
Форма обучения: вечер
Номер личного дела: Проверил:
Калуга 2008
Задача 1
По предприятиям
легкой промышленности региона получена информация, характеризующая зависимость
объема выпуска продукции (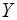 , млн. руб.) от объема капиталовложений (
, млн. руб.) от объема капиталовложений (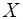 , млн. руб.)
, млн. руб.)
Требуется:
1.
Найти параметры уравнения линейной регрессии, дать
экономическую интерпретацию коэффициента регрессии.
2.
Вычислить остатки; найти остаточную сумму квадратов; оценить
дисперсию остатков 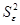 ; построить график остатков.
; построить график остатков.
3.
Проверить выполнение предпосылок МНК.
4.
Осуществить проверку значимости параметров уравнения
регрессии с помощью t-критерия Стьюдента 
5.
Вычислить коэффициент детерминации, проверить значимость
уравнения регрессии с помощью 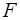 - критерия Фишера
- критерия Фишера 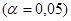 , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
6.
Осуществить прогнозирование среднего значения показателя 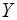 при уровне
значимости
при уровне
значимости 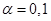 , если прогнозное значения фактора Х составит
80% от его максимального значения.
, если прогнозное значения фактора Х составит
80% от его максимального значения.
7.
Представить графически: фактические и модельные значения 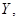 точки прогноза.
точки прогноза.
8.
Составить уравнения нелинейной регрессии:
·
гиперболической;
·
степенной;
·
показательной.
Привести графики построенных уравнений регрессии.
9.
Для указанных моделей найти коэффициенты детерминации,
коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим
характеристикам и сделать вывод.
|
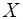
|
72
|
52
|
73
|
74
|
76
|
79
|
54
|
68
|
73
|
64
|
|
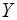
|
121
|
84
|
119
|
117
|
129
|
128
|
102
|
111
|
112
|
98
|
РЕШЕНИЕ:
1). Найти
параметры уравнения линейной регрессии, дать экономическую интерпретацию
коэффициента регрессии.
Таблица
1
|
Наблюдение
|
Объем капиталовложений,
млн. руб.(X)
|
Объем выпуска продукции, млн. руб. (Y)
|
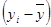
|
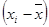
|
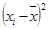
|
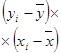
|
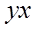
|
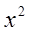
|
|
1
|
72
|
121
|
8,9
|
3,5
|
12,25
|
31,15
|
8712
|
5184
|
|
2
|
52
|
84
|
-28,1
|
-16,5
|
272,25
|
463,65
|
4368
|
2704
|
|
3
|
73
|
119
|
6,9
|
4,5
|
20,25
|
31,05
|
8687
|
5329
|
|
4
|
74
|
117
|
4,9
|
5,5
|
30,25
|
26,95
|
8658
|
5476
|
|
5
|
76
|
129
|
16,9
|
7,5
|
56,25
|
126,75
|
9804
|
5776
|
|
6
|
79
|
128
|
15,9
|
10,5
|
110,25
|
166,95
|
10112
|
6241
|
|
7
|
54
|
102
|
-10,1
|
-14,5
|
210,25
|
146,45
|
5508
|
2916
|
|
8
|
68
|
111
|
-1,1
|
-0,5
|
0,25
|
0,55
|
7548
|
4624
|
|
9
|
73
|
112
|
-0,1
|
4,5
|
20,25
|
-0,45
|
8176
|
5329
|
|
10
|
64
|
98
|
-14,1
|
-4,5
|
20,25
|
63,45
|
6272
|
4096
|
|
Сумма
|
685
|
1121
|
0,0
|
0,0
|
752,5
|
1 056,5
|
77845,0
|
47675,0
|
|
Среднее
|
68,5
|
112,1
|
|
|
|
|
7 784,5
|
4 767,5
|
Для вычисления
параметров модели следует воспользоваться формулами и расчетными данными из
таблицы 1.
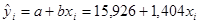 Модель зависимости объема
выпуска продукции от объема капиталовложений имеет вид
Модель зависимости объема
выпуска продукции от объема капиталовложений имеет вид
Рис. 1
С увеличением
объемов капиталовложений на 1 млн. руб. объем выпускаемой продукции увеличится в среднем на 1,404 млн. руб.
2). Вычислить
остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 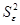 ; построить график остатков.
; построить график остатков.
и т.д.
Таблица 2
|
ВЫВОД ОСТАТКОВ
|
|
Наблюдение
|
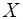
|
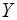
|
 Предсказанное, Предсказанное,
|
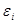 Остатки, Остатки,
|
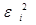
|
|
1
|
72
|
121
|
117,01
|
3,99
|
15,92
|
|
2
|
52
|
84
|
88,93
|
-4,93
|
24,30
|
|
3
|
73
|
119
|
118,42
|
0,58
|
0,34
|
|
4
|
74
|
117
|
119,82
|
-2,82
|
7,95
|
|
5
|
76
|
129
|
122,63
|
6,37
|
40,58
|
|
6
|
79
|
128
|
126,84
|
1,16
|
1,35
|
|
7
|
54
|
102
|
91,74
|
10,26
|
105,27
|
|
8
|
68
|
111
|
111,40
|
-0,40
|
0,16
|
|
9
|
73
|
112
|
118,42
|
-6,42
|
41,22
|
|
10
|
64
|
98
|
105,78
|
-7,78
|
60,53
|
|
ИТОГО
|
685
|
1121
|
1120,99
|
0
|
297,61
|
Дисперсия остатков равна
Рис.
2
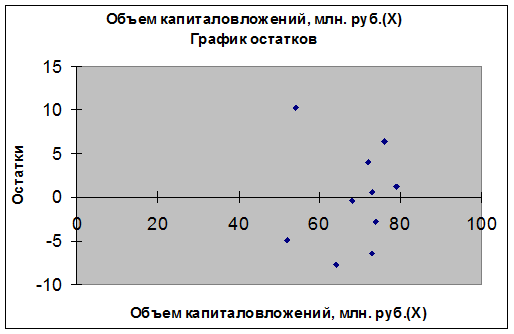
3). Проверить выполнение предпосылок МНК.
Проверка
выполнения предпосылок МНК выполняется на основе анализа остаточной компоненты.
Оценим адекватность построенной модели,
используя свойства независимости остаточной компоненты, случайности и
соответствия нормальному закону распределения (при использовании R/S-критерия
взять табулированные границы 2,7—3,7).
Модель является адекватной, если математическое ожидание
значений остаточного ряда случайны, независимы и подчинены нормальному закону
распределения.[1]
3.1. Проверим независимость (отсутствие автокорреляции) с помощью d – критерия Дарбина –
Уотсона по
формуле: 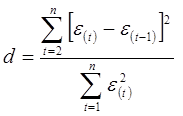
Используем данные табл. 3
Таблица 3
|
Наблюдение
|
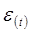
|
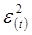 
|
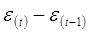
|
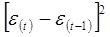
|
|
1
|
3,99
|
15,92
|
-
|
-
|
|
2
|
-4,93
|
24,30
|
-8,92
|
79,57
|
|
3
|
0,58
|
0,34
|
5,51
|
30,36
|
|
4
|
-2,82
|
7,95
|
-3,4
|
11,56
|
|
5
|
6,37
|
40,58
|
9,19
|
84,46
|
|
6
|
1,16
|
1,35
|
-5,21
|
27,14
|
|
7
|
10,26
|
105,27
|
9,1
|
82,81
|
|
8
|
-0,40
|
0,16
|
-10,66
|
113,64
|
|
9
|
-6,42
|
41,22
|
-6,02
|
36,24
|
|
10
|
-7,78
|
60,53
|
-1,36
|
1,85
|
|
Сумма
|
0
|
297,61
|
|
467,62
|
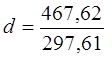 ,
, 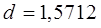
Т.к. расчетное значение
d попадает в интервал от d2 до 2 (рис. 4.7). Свойство
независимости выполняется. Следовательно, модель по этому критерию адекватна.
Анализ независимости с
помощью критерия Дарбина – Уотсона Рис. 3
|
1)
|
|
|
2)
|
|
3)
|
|
4)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d1
|
d2
|
|
2
|
|
|
4
|
|
свойство не выполняется
|
применять другой
критерий
|
свойство выполняется
|
преобразовать dn=4-d
|
|
0
|
d1
|
d2
|
|
2
|
|
|
4
|
|
|
1,08
|
1,36
|
1,5712
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|r(1)|<0,36
|
|
|
|
|
|
3.2. Проверку случайности уровней ряда остатков
проведем на основе критерия поворотных точек. P > [2/3(n-2) –
1, 96 – (16n-29)/90]
Количество поворотных точек равно 6 (рис. 4).
Рис. 4
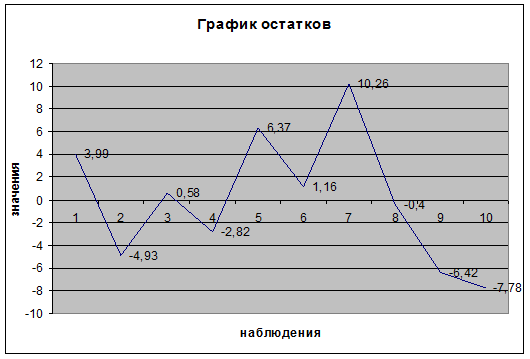
Неравенство
выполняется (6 > 2). Следовательно, свойство случайности выполняется. Модель
по этому критерию адекватна.
3.3. Соответствие ряда остатков нормальному
закону распределения определим при помощи RS – критерия:
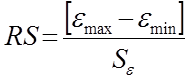 , где
, где
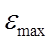 - максимальный уровень
ряда остатков,
- максимальный уровень
ряда остатков, 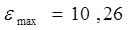
 - минимальный уровень
ряда остатков,
- минимальный уровень
ряда остатков, 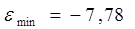
 -
среднеквадратическое отклонение,
-
среднеквадратическое отклонение,
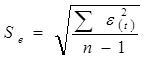 ,
, 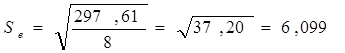

Расчетное
значение попадает в интервал (2,7-3,7), следовательно, выполняется свойство
нормальности распределения. Модель по этому критерию адекватна.
3.4. Проверка равенства нулю математического
ожидания уровней ряда остатков.
В нашем случае 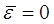 , поэтому гипотеза о равенстве математического ожидания
значений остаточного ряда нулю выполняется.
, поэтому гипотеза о равенстве математического ожидания
значений остаточного ряда нулю выполняется.
3.5. Обнаружение гетероскедастичности.
Чтобы оценить
нарушение гомоскедастичности по тесту Гольфельда-Квандта, необходимо
упорядочить имеющиеся наблюдения по мере возрастания, разделить совокупности на
две группы, определить уравнения регрессии (с помощью Excel), определить остаточные
суммы квадратов для регрессии, вычислить отношение между ними и сравнить с F-
критерием.
|
х1
|
У1
|
ŷ1
|
ε²1
|
|
х2
|
У2
|
ŷ2
|
ε²2
|
|
52
|
84
|
95,71
|
137,11
|
|
73
|
119
|
116,23
|
7,67
|
|
54
|
102
|
97,68
|
18,70
|
|
73
|
112
|
116,23
|
17,90
|
|
64
|
98
|
107,51
|
90,41
|
|
74
|
117
|
118,62
|
2,61
|
|
68
|
111
|
111,44
|
0,19
|
|
76
|
129
|
123,38
|
31,53
|
|
72
|
121
|
115,37
|
31,65
|
|
79
|
128
|
130,54
|
6,44
|
|
|
|
сумма
|
278,06
|
|
|
|
сумма
|
66,15
|
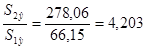
Используя
надстройки Excel, найдем F – критерий равный 6,389.
Наблюдаемое F =
4,203 меньше критического, что означает, что модель гомоскедастична.
В таблице 4 собраны данные
анализа ряда остатков.
Анализ ряда остатков Таблица 4
|
Проверяемое свойство
|
Используемые статистики
|
Граница
|
Вывод
|
|
наименование
|
значение
|
нижняя
|
верхняя
|
|
Независимость
|
d – критерий Дарбина-Уотсона
|
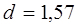
|
1,36
|
2
|
адекватна
|
|
Случайность
|
Критерий пиков (поворотных точек)
|
6 > 2
|
2
|
адекватна
|
|
Нормальность
|
RS – критерий
|
2,96
|
2,7
|
3,7
|
адекватна
|
|
Среднее = 0 ?
|
t – статистика
Стьюдента
|
0,000
|
-2,179
|
2,179
|
адекватна
|
|
Вывод: модель статистически адекватна
|
4). Осуществить проверку значимости параметров
уравнения регрессии с помощью t-критерия Стьюдента 
Проверка
значимости отдельных коэффициентов регрессии связана с определением расчетных
значений t – критерия (t – статистики) для
соответствующих коэффициентов регрессии:
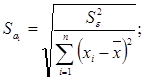
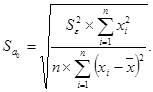
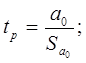
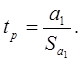
Где
Расчетная
таблица
Таблица
5
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
|
Y-пересечение
|
а0
|
15,927
|
15,352
|
1,037
|
|
Объем
капиталовложений,
млн.
руб.(X)
|
а1
|
1,404
|
0,222
|
6,315
|
Сравнивая
расчетное значение с табличным значением (при n-2 и степеней свободы 0,05 табличное равно 2,306004). Делаем
вывод о том, что фактор а0
следует исключить из модели, так как расчетное значение t меньше табличного (при этом качество модели не ухудшится).
5). Вычислить коэффициент детерминации, проверить
значимость уравнения регрессии с помощью 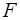 - критерия Фишера
- критерия Фишера 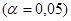 , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
Коэффициент
множественной корреляции (индекс корреляции), возведенный в квадрат (R2), называется коэффициентом
детерминации.
Таблица
6
Расчет
коэффициента детерминации
|
Наблюдение
|
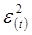 
|
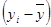
|
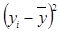
|
|
1
|
15,92
|
8,9
|
79,21
|
|
2
|
24,30
|
-28,1
|
789,61
|
|
3
|
0,34
|
6,9
|
47,61
|
|
4
|
7,95
|
4,9
|
24,01
|
|
5
|
40,58
|
16,9
|
285,61
|
|
6
|
1,35
|
15,9
|
252,81
|
|
7
|
105,27
|
-10,1
|
102,01
|
|
8
|
0,16
|
-1,1
|
1,21
|
|
9
|
41,22
|
-0,1
|
0,01
|
|
10
|
60,53
|
-14,1
|
198,81
|
|
Сумма
|
297,61
|
0,0
|
1780,9
|
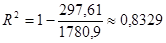
Чем ближе R2 к 1, тем качество модели лучше.
Вариация
результата Y (объема выпуска продукции) на 83,29 % объясняется вариацией
фактора X (объемом капиталовложений).
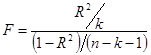 Для проверки значимости
модели регрессии используется F – критерий Фишера, вычисляемый как отношение
дисперсии исходного ряда и несмещенной дисперсии остаточной компоненты. Если
расчетное значение больше табличного при заданном уровне значимости, то модель
считается значимой.
Для проверки значимости
модели регрессии используется F – критерий Фишера, вычисляемый как отношение
дисперсии исходного ряда и несмещенной дисперсии остаточной компоненты. Если
расчетное значение больше табличного при заданном уровне значимости, то модель
считается значимой.
, где k – количество факторов,
включенных в модель.
F > Fтаб. =5, 32 для a = 0, 05; k1 = 1, k2 = 8.
Уравнение регрессии с
вероятностью 0,95 в целом статистически значимое, т.к. F > Fтаб.
Оценим точность
модели на основе использования средней
относительной ошибки аппроксимации.
Для оценки точности полученной модели будем
использовать показатель относительной ошибки аппроксимации, который вычисляется
по формуле:
 , где
, где 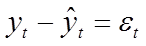
Таблица 7
Расчет
относительной ошибки аппроксимации
|
Наблюдение
|
Y
|
Предсказанное Y
|
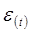
|
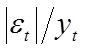
|
|
1
|
121
|
117,01
|
3,99
|
0,03
|
|
2
|
84
|
88,93
|
-4,93
|
0,06
|
|
3
|
119
|
118,42
|
0,58
|
0,005
|
|
4
|
117
|
119,82
|
-2,82
|
0,02
|
|
5
|
129
|
122,63
|
6,37
|
0,05
|
|
6
|
128
|
126,84
|
1,16
|
0,01
|
|
7
|
102
|
91,74
|
10,26
|
0,10
|
|
8
|
111
|
111,40
|
-0,40
|
0,00
|
|
9
|
112
|
118,42
|
-6,42
|
0,06
|
|
10
|
98
|
105,78
|
-7,78
|
0,08
|
|
Сумма
|
1121
|
1120,99
|
0
|
0,41
|
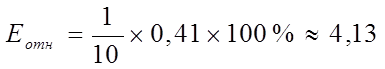
В среднем расчетные значения предсказанного у для
линейной модели отличаются от фактических значений на 4,13 %.
Если ошибка, вычисленная по формуле, не превосходит
15%, точность модели считается приемлемой.
6). Осуществить
прогнозирование среднего значения показателя 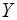 при уровне
значимости
при уровне
значимости 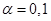 , если прогнозное значения фактора Х составит
80% от его максимального значения.
, если прогнозное значения фактора Х составит
80% от его максимального значения.
Прогнозное значение Х = 79*80 % = 63,2
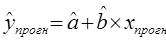 Прогнозируемое значение
переменной у получается при
подстановке в уравнение регрессии
Прогнозируемое значение
переменной у получается при
подстановке в уравнение регрессии
ожидаемой величины фактора х.
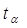
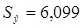 Используя данные таблицы 2,
найдем величину отклонения от линии регрессии.
Используя данные таблицы 2,
найдем величину отклонения от линии регрессии.
Коэффициент
Стьюдента для m = 8 степеней свободы (m = n-2) и уровня значимости 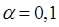 равен 3,3554.
равен 3,3554.
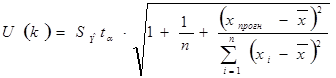
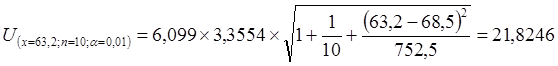
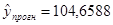 Таким образом, прогнозное
значение будет
находиться между верхней границей, равной 104,6588 + 21,8246 = 126,4834 и
нижней границей, равной 104,6588 - 21,8246 = 82,8342.
Таким образом, прогнозное
значение будет
находиться между верхней границей, равной 104,6588 + 21,8246 = 126,4834 и
нижней границей, равной 104,6588 - 21,8246 = 82,8342.
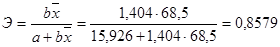 Эластичность линейной модели
равна
Эластичность линейной модели
равна
На 85,79%
изменяется Y (объема выпуска продукции)
при изменении фактора X (объемом капиталовложений) на один процент.
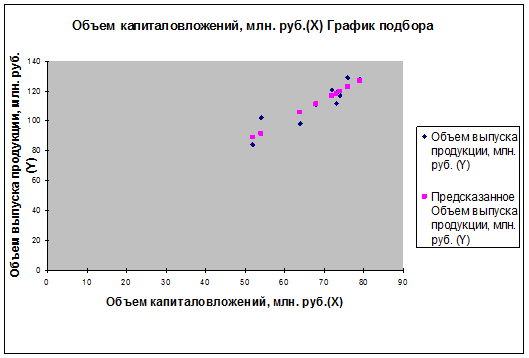
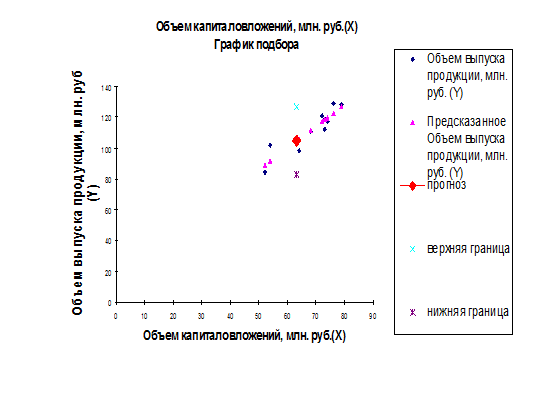
Преобразуем график подбора (рис. 1), дополнив его данными
прогноза.
Рис. 5
8). Составить
уравнения нелинейной регрессии:
·
гиперболической;
·
степенной;
·
показательной.
Привести графики построенных уравнений регрессии.
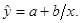 8.1. Составить уравнения нелинейной регрессии гиперболической.
8.1. Составить уравнения нелинейной регрессии гиперболической.
Уравнение
гиперболической функции
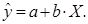
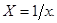 Произведем линеаризацию
модели путем замены В
результате получим линейное уравнение
Произведем линеаризацию
модели путем замены В
результате получим линейное уравнение
Рассчитаем его
параметры по данным таблицы 8.
Таблица
8
|
Гиперболическая
модель
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наблюдение
|
x
|
y
|
X
|
yX
|
X^2
|
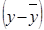
|
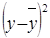
|
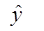
|
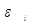
|
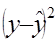
|
|ε/y|*100%
|
|
1
|
72
|
121
|
0,0139
|
1,6806
|
0,0001929
|
8,9
|
79,21
|
117,551
|
3,449
|
11,899
|
2,851
|
|
2
|
52
|
84
|
0,0192
|
1,6154
|
0,0003698
|
-28,1
|
789,61
|
87,861
|
-3,861
|
14,911
|
4,597
|
|
3
|
73
|
119
|
0,0137
|
1,6301
|
0,0001877
|
6,9
|
47,61
|
118,608
|
0,392
|
0,154
|
0,329
|
|
4
|
74
|
117
|
0,0135
|
1,5811
|
0,0001826
|
4,9
|
24,01
|
119,637
|
-2,637
|
6,953
|
2,254
|
|
5
|
76
|
129
|
0,0132
|
1,6974
|
0,0001731
|
16,9
|
285,61
|
121,613
|
7,387
|
54,564
|
5,726
|
|
6
|
79
|
128
|
0,0127
|
1,6203
|
0,0001602
|
15,9
|
252,81
|
124,390
|
3,610
|
13,030
|
2,820
|
|
7
|
54
|
102
|
0,0185
|
1,8889
|
0,0003429
|
-10,1
|
102,01
|
91,820
|
10,180
|
103,632
|
9,980
|
|
8
|
68
|
111
|
0,0147
|
1,6324
|
0,0002163
|
-1,1
|
1,21
|
113,010
|
-2,010
|
4,040
|
1,811
|
|
9
|
73
|
112
|
0,0137
|
1,5342
|
0,0001877
|
-0,1
|
0,01
|
118,608
|
-6,608
|
43,665
|
5,900
|
|
10
|
64
|
98
|
0,0156
|
1,5313
|
0,0002441
|
-14,1
|
198,81
|
107,902
|
-9,902
|
98,042
|
10,104
|
|
Сумма
|
685
|
1121
|
0,1487
|
16,412
|
0,0022573
|
|
1 780,9
|
1121,0
|
0,00
|
350,888
|
46,373
|
|
Среднее
|
68,5
|
112,1
|
0,01487
|
1,6412
|
0,0002257
|
|
|
|
|
|
4,637
|
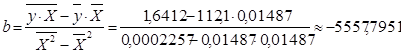
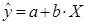 Получим следующее уравнение
гиперболической модели:
Получим следующее уравнение
гиперболической модели:
Определим индекс корреляции:
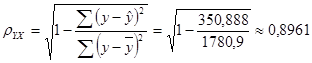
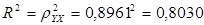 Связь между показателем у и фактором х можно считать достаточно сильной.
Связь между показателем у и фактором х можно считать достаточно сильной.
Индекс детерминации:
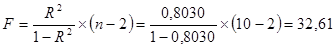 Вариация результата Y (объема выпуска продукции) на 80,30% объясняется вариацией
фактора X (объемом капиталовложений).
Вариация результата Y (объема выпуска продукции) на 80,30% объясняется вариацией
фактора X (объемом капиталовложений).
Рассчитаем F-
критерий Фишера:
F > Fтаб. =5,
32 для a = 0, 05; k1 = 1,
k2 = 8.
Уравнение регрессии с
вероятностью 0,95 в целом статистически значимое, т.к. F > Fтаб.
Средняя относительная ошибка
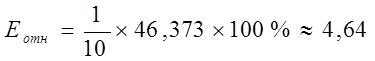
В среднем
расчетные значения для
гиперболической модели отличаются от фактических значений на 4,64%.
Эластичность
гиперболической модели равна
На 71,42%
изменяется Y (объема выпуска продукции)
при изменении фактора X (объемом капиталовложений) на один процент.
Рис. 6
Гиперболическая
модель
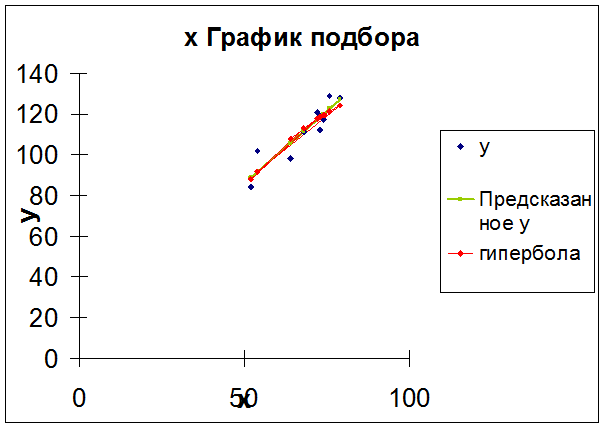
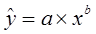 8.2. Составить уравнения нелинейной регрессии степенной.
8.2. Составить уравнения нелинейной регрессии степенной.
Уравнение степенной модели
имеет вид:
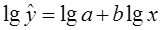 Для построения этой модели необходимо
произвести линеаризацию переменных. Для этого произведем логарифмирование обеих
частей уравнения:
Для построения этой модели необходимо
произвести линеаризацию переменных. Для этого произведем логарифмирование обеих
частей уравнения:
Таблица 9
Логарифмирование
|
Наблюдение
|
y
|
lg(y)
|
x
|
lg(x)
|
|
1
|
121
|
2,0828
|
72
|
1,8573
|
|
2
|
84
|
1,9243
|
52
|
1,7160
|
|
3
|
119
|
2,0755
|
73
|
1,8633
|
|
4
|
117
|
2,0682
|
74
|
1,8692
|
|
5
|
129
|
2,1106
|
76
|
1,8808
|
|
6
|
128
|
2,1072
|
79
|
1,8976
|
|
7
|
102
|
2,0086
|
54
|
1,7324
|
|
8
|
111
|
2,0453
|
68
|
1,8325
|
|
9
|
112
|
2,0492
|
73
|
1,8633
|
|
10
|
98
|
1,9912
|
64
|
1,8062
|
|
Сумма
|
1121
|
20,4630
|
685
|
18,3187
|
|
Среднее
|
112,1
|
2,0463
|
68,5
|
1,8319
|
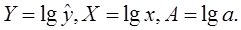
Обозначим
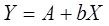 Тогда уравнение примет
вид: линейное
уравнение регрессии.
Тогда уравнение примет
вид: линейное
уравнение регрессии.
Рассчитаем его
параметры, используя данные таблицы 10.
Таблица
10
|
|
|
Степенная модель
|
|
|
|
|
|
|
|
|

|

|

|

|
|
|
Наблюдение
|
y
|
Y
|
x
|
X
|
Y X
|

X^2
|
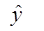
|
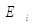
|
|ε/y|*100%
|
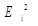
|
|
1
|
121
|
2,0828
|
72
|
1,8573
|
3,86842
|
3,4497
|
116,862
|
4,138
|
3,420
|
17,122
|
|
2
|
84
|
1,9243
|
52
|
1,7160
|
3,30207
|
2,9447
|
88,874
|
-4,874
|
5,802
|
23,754
|
|
3
|
119
|
2,0755
|
73
|
1,8633
|
3,86741
|
3,4720
|
118,226
|
0,774
|
0,650
|
0,599
|
|
4
|
117
|
2,0682
|
74
|
1,8692
|
3,86592
|
3,4940
|
119,587
|
-2,587
|
2,211
|
6,694
|
|
5
|
129
|
2,1106
|
76
|
1,8808
|
3,96963
|
3,5375
|
122,301
|
6,699
|
5,193
|
44,882
|
|
6
|
128
|
2,1072
|
79
|
1,8976
|
3,99870
|
3,6010
|
126,350
|
1,650
|
1,289
|
2,724
|
|
7
|
102
|
2,0086
|
54
|
1,7324
|
3,47969
|
3,0012
|
91,741
|
10,259
|
10,058
|
105,250
|
|
8
|
111
|
2,0453
|
68
|
1,8325
|
3,74807
|
3,3581
|
111,376
|
-0,376
|
0,338
|
0,141
|
|
9
|
112
|
2,0492
|
73
|
1,8633
|
3,81835
|
3,4720
|
118,226
|
-6,226
|
5,559
|
38,765
|
|
10
|
98
|
1,9912
|
64
|
1,8062
|
3,59651
|
3,2623
|
105,837
|
-7,837
|
7,997
|
61,425
|
|
Сумма
|
1121
|
20,4630
|
685
|
18,3187
|
37,5148
|
33,5923
|
|
1,621
|
42,52
|
301,355
|
|
Среднее
|
112,1
|
2,0463
|
68,5
|
1,8319
|
3,7515
|
3,3592
|
|
|
|
|
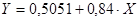
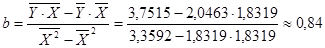
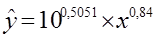 Перейдем
к исходным переменным x и y:
Перейдем
к исходным переменным x и y:
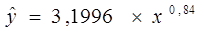
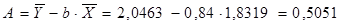 Получим уравнение степенной модели регрессии:
Получим уравнение степенной модели регрессии:
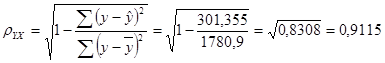 Определим индекс корреляции:
Определим индекс корреляции:
Связь между показателем у и фактором х можно считать достаточно сильной.
Коэффициент детерминации
равен 0,8308:
Вариация
результата Y (объема выпуска продукции)
на 83,08% объясняется вариацией фактора X (объемом капиталовложений).
Рассчитаем F-
критерий Фишера:
F > Fтаб. =5,
32 для a = 0,05; k1 = 1, k2 = 8.
Уравнение регрессии с
вероятностью 0,95 в целом статистически значимое, т.к. F > Fтаб.
Средняя относительная ошибка
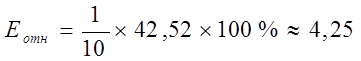
В среднем
расчетные значения для степенной
модели отличаются от фактических значений на 4,25%.
Эластичность
степенной модели равна
На 84,0%
изменяется Y (объема выпуска продукции)
при изменении фактора X (объемом капиталовложений) на один процент.
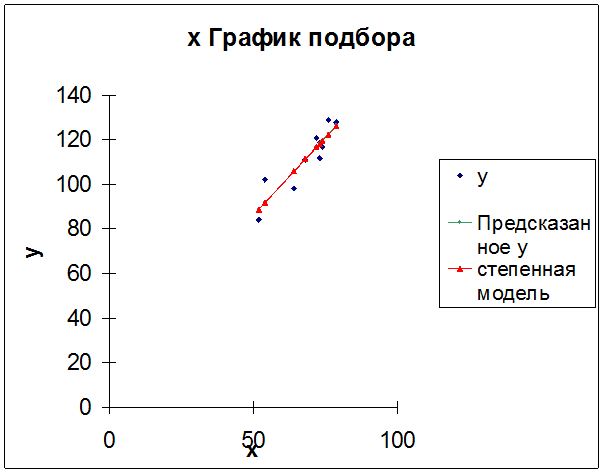
Рис. 7
Степенная
модель
 8.3. Составить уравнения нелинейной
регрессии показательной.
8.3. Составить уравнения нелинейной
регрессии показательной.
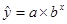 Уравнение показательной
кривой:
Уравнение показательной
кривой:
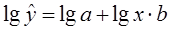 Для построения этой модели
необходимо произвести линеаризацию переменных. Для этого осуществим
логарифмирование обеих частей уравнения:
Для построения этой модели
необходимо произвести линеаризацию переменных. Для этого осуществим
логарифмирование обеих частей уравнения:
Обозначим
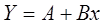 Получим линейное уравнение
регрессии:
Получим линейное уравнение
регрессии:
Рассчитаем его параметры,
используя данные таблицы 11.
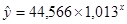 Перейдем к исходным
переменным, выполнив потенцирование данного уравнения:
Перейдем к исходным
переменным, выполнив потенцирование данного уравнения:
Определим индекс корреляции:
Связь между показателем у и фактором х можно считать сильной.
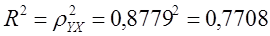 Коэффициент детерминации
равен 0,7708.
Коэффициент детерминации
равен 0,7708.
Вариация
результата Y (объема выпуска продукции)
на 77,08% объясняется вариацией фактора X (объемом капиталовложений).
Рассчитаем F-
критерий Фишера:
F > Fтаб. =5, 32 для a = 0,05; k1 = 1, k2 = 8.
Уравнение регрессии с
вероятностью 0,95 в целом статистически значимое, т.к. F > Fтаб.
Средняя относительная ошибка
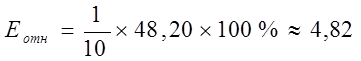
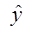 В среднем расчетные
значения для показательной модели
отличаются от фактических значений на 4,82%.
В среднем расчетные
значения для показательной модели
отличаются от фактических значений на 4,82%.
Рис. 8
Показательная модель
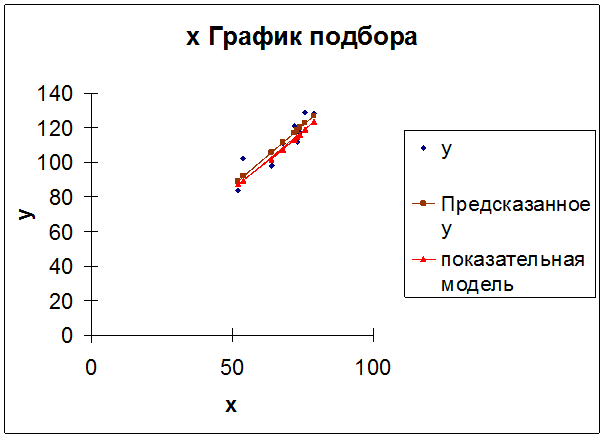
Таблица 11
|
Показательная модель
|
|
|
|
|
|
|
|
 
|
|
|
|
|
|
|
|
|
Наблюдение
|
y
|
У
|
x
|
Ух
|
x^2
|
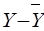  
|
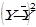
|
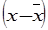
|
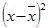
|
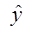
|
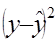
|
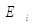
|
|ε/y|*100%
|
|
1
|
121
|
2,0828
|
72
|
149,96
|
5184
|
0,0365
|
0,0013
|
3,5
|
12,25
|
112,95
|
64,81
|
8,051
|
6,653
|
|
2
|
84
|
1,9243
|
52
|
100,06
|
2704
|
-0,1220
|
0,0149
|
-16,5
|
272,25
|
87,24
|
10,47
|
-3,236
|
3,852
|
|
3
|
119
|
2,0755
|
73
|
151,51
|
5329
|
0,0293
|
0,0009
|
4,5
|
20,25
|
114,42
|
21,00
|
4,582
|
3,851
|
|
4
|
117
|
2,0682
|
74
|
153,05
|
5476
|
0,0219
|
0,0005
|
5,5
|
30,25
|
115,91
|
1,20
|
1,095
|
0,936
|
|
5
|
129
|
2,1106
|
76
|
160,40
|
5776
|
0,0643
|
0,0041
|
7,5
|
56,25
|
118,94
|
101,24
|
10,062
|
7,800
|
|
6
|
128
|
2,1072
|
79
|
166,47
|
6241
|
0,0609
|
0,0037
|
10,5
|
110,25
|
123,64
|
19,03
|
4,363
|
3,408
|
|
7
|
102
|
2,0086
|
54
|
108,46
|
2916
|
-0,0377
|
0,0014
|
-14,5
|
210,25
|
89,52
|
155,78
|
12,481
|
12,237
|
|
8
|
111
|
2,0453
|
68
|
139,08
|
4624
|
-0,0010
|
0,0000
|
-0,5
|
0,25
|
107,26
|
13,97
|
3,738
|
3,368
|
|
9
|
112
|
2,0492
|
73
|
149,59
|
5329
|
0,0029
|
0,0000
|
4,5
|
20,25
|
114,42
|
5,85
|
-2,418
|
2,159
|
|
10
|
98
|
1,9912
|
64
|
127,44
|
4096
|
-0,0551
|
0,0030
|
-4,5
|
20,25
|
101,86
|
14,91
|
-3,861
|
3,940
|
|
Сумма
|
1121
|
20,4630
|
685
|
1406,04
|
47 675
|
|
0,0299
|
|
752,50
|
|
408,26
|
34,857
|
48,20
|
|
Среднее
|
112,1
|
2,0463
|
68,5
|
140,604
|
4 767,5
|
|
|
|
|
|
40,826
|
|
4,82
|
Для выбора
лучшей модели построим сводную таблицу результатов (табл. 12).
Таблица
12
|
параметры/модель
|
Коэффициент детерминации R^2
|
F - критерий Фишера
|
Индекс корреляции рxy
|
Средняя относительная ошибка
|
|
|
|
Линейная
|
0,8329
|
39,88
|
0,9126
|
4,13
|
|
|
Гиперболическая
|
0,8030
|
32,61
|
0,8961
|
4,64
|
|
|
Степенная
|
0,8308
|
39,29
|
0,9115
|
4,25
|
|
|
Показательная
|
0,7708
|
26,9
|
0,8779
|
4,82
|
|
Все модели имеют
примерно одинаковые характеристики, но большее значение F –
критерия Фишера и большее значение коэффициента R2 имеет линейная модель. Её
можно взять в качестве лучшей для построения прогноза.
Задача 2
Даны
две СФМ, которые заданы в виде матриц коэффициентов модели. Необходимо записать
системы одновременных уравнений и проверить обе системы на идентифицируемость.
|
Номер уравнения
|
А
|
Б
|
|
переменные
|
переменные
|
|
у1
|
у2
|
у3
|
х1
|
х2
|
х3
|
х4
|
у1
|
у2
|
у3
|
х1
|
х2
|
х3
|
х4
|
|
1
|
-1
|
0
|
b13
|
а11
|
a12
|
а13
|
0
|
-1
|
b12
|
0
|
а11
|
a12
|
а13
|
0
|
|
2
|
b21
|
-1
|
b23
|
0
|
0
|
а23
|
a24
|
0
|
-1
|
b23
|
а21
|
0
|
а23
|
a24
|
|
3
|
0
|
b32
|
-1
|
а31
|
0
|
a33
|
а34
|
0
|
b32
|
-1
|
а31
|
0
|
a33
|
а34
|
Решение
А) Составим структурную
модель:
y1 = b13y3 + a11x1
+ a12x2 + a13x3
y2 = b21y1 + b23y3
+ a23x3 + a24x4
y3 = b32у2 + a31x1 + a33x3 + а34х4
Проверим каждое уравнение системы на выполнение необходимого и
достаточного условия идентификации.
В первом уравнении две
эндогенные переменные: у1 и у3 (Н = 2). В нем отсутствует
экзогенная переменная х4 (D = 1). Необходимое условие
идентификации D + 1 = Н выполнено.
Для проверки на достаточное
условие составим матрицу из коэффициентов при переменных у2 и х4.
Таблица 1
Матрица, составленная из
коэффициентов при переменных у2 и х4
|
Уравнения, из которых взяты
коэффициенты при переменных
|
Переменные
|
|
у2
|
x4
|
|
2
|
-1
|
a24
|
|
3
|
b32
|
а34
|
В первом столбце таблицы
показано, что коэффициенты взяты из уравнений 2 и 3 системы.
Определитель представленной
в табл. 1 матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное
условие выполнено, и первое уравнение идентифицируемо.
Во втором уравнении три
эндогенные переменные: у1, у2 и у3 (Н = 3). В
нем отсутствуют экзогенные переменные х1 и х2 (D = 2).
Необходимое условие идентификации D + 1 = Н выполнено.
Для проверки на достаточное
условие составим матрицу из коэффициентов при переменных х1 и x2,
которые отсутствуют во втором уравнении (табл. 2).
Таблица 2
Матрица, составленная из коэффициентов при переменных х1 и х2
|
Уравнения, из которых взяты
коэффициенты при переменных
|
Переменные
|
|
х1
|
x2
|
|
1
|
а11
|
a12
|
|
3
|
а31
|
0
|
Определитель представленной
в табл. 2 матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное
условие выполнено, и второе уравнение идентифицируемо.
В третьем уравнении две
эндогенные переменные: у2 и у3 (Н = 2). В нем отсутствует
экзогенная переменная х2 (D = 1). Необходимое условие
идентификации D + 1 = Н выполнено.
Для проверки на достаточное
условие составим матрицу из коэффициентов при переменных у1 и х2,
которые отсутствуют в третьем уравнении (табл. 3).
Таблица 3
Матрица, составленная из коэффициентов при переменных у1 и х2
|
Уравнения, из которых взяты
коэффициенты при переменных
|
Переменные
|
|
у1
|
x2
|
|
1
|
-1
|
a12
|
|
2
|
b21
|
0
|
Определитель представленной
в табл. 3 матрицы не равен нулю, а ранг матрицы равен 2. Значит, достаточное
условие выполнено, и третье уравнение идентифицируемо.
СФМ идентифицируема так как
каждое ее уравнение идентифицируемо.
Б) Составим структурную
модель:
y1 = b12y2 + a11x1
+ a12x2 + а13х3
y2 = b23y3 + а21х1 + a23x3 + a24x4
y3 = b32y2 + а31x1 + a33x3
+ a34x4
Проверим каждое уравнение
системы на выполнение необходимого и достаточного условия идентификации.
В первом уравнении две
эндогенные переменные: у1, и у2 (Н = 2). В нем
отсутствует экзогенная переменная х4 (D = 1). Необходимое условие
идентификации D + 1 = Н выполнено.
Для проверки на достаточное
условие составим матрицу из коэффициентов при переменных у3 и х4.
Таблица 4
Матрица, составленная из
коэффициентов при переменных у3 и х4
|
Уравнения, из которых взяты
коэффициенты при переменных
|
Переменные
|
|
у3
|
x4
|
|
2
|
b23
|
a24
|
|
3
|
-1
|
а34
|
В первом столбце таблицы
показано, что коэффициенты взяты из уравнений 2 и 3 системы.
Определитель представленной
в табл. 4 матрицы не равен нулю, достаточное условие выполнено, и первое
уравнение идентифицируемо.
Во втором уравнении две
эндогенные переменные: у2 и у3 (Н = 2). В нем отсутствует
экзогенная переменная х2 (D = 1). Необходимое условие
идентификации D + 1 = Н выполнено.
Для проверки на достаточное
условие составим матрицу из коэффициентов при переменных у1 и x2,
которые отсутствуют во втором уравнении (табл. 5).
Таблица 5
Матрица, составленная из коэффициентов при переменных у1 и х2
|
Уравнения, из которых взяты
коэффициенты при переменных
|
Переменные
|
|
у1
|
x2
|
|
1
|
-1
|
a12
|
|
3
|
0
|
0
|
Определитель представленной
в табл. 5 матрицы равен нулю (так как вторая строка равна нулю), а ранг матрицы
равен 2. Значит, достаточное условие не выполнено, и второе уравнение
неидентифицируемо.
В третьем уравнении две
эндогенные переменные: у2 и у3 (Н = 2). В нем отсутствует
экзогенная переменная х2 (D = 1). Необходимое условие
идентификации D + 1 = Н выполнено.
Для проверки на достаточное
условие составим матрицу из коэффициентов при переменных у1 и х2,
которые отсутствуют в третьем уравнении (табл. 6).
Таблица 6
Матрица, составленная из коэффициентов при переменных у1 и х2
|
Уравнения, из которых взяты
коэффициенты при переменных
|
Переменные
|
|
у1
|
x2
|
|
1
|
-1
|
a12
|
|
2
|
0
|
0
|
Так как вторая строка
матрицы состоит из нулей, определитель матрицы равен нулю. Значит, достаточное
условие не выполнено, и третье уравнение нельзя считать идентифицируемым.
СФМ неидентифицируема так
как не все ее уравнение идентифицируемы.
В) По данным таблицы,
используя косвенный метод наименьших квадратов, построить структурную форму
модели вида:
y1 = а01 + b12y2
+ a11x1 + ε1
y2 = а02 + b21y1
+ a22x2 + ε2
|
n
|
y1
|
y2
|
x1
|
x2
|
|
1
|
28,3
|
51,7
|
7
|
12
|
|
2
|
4,4
|
11,5
|
1
|
1
|
|
3
|
33,1
|
64,6
|
10
|
14
|
|
4
|
14,6
|
38,4
|
9
|
4
|
|
5
|
35,9
|
64,1
|
7
|
17
|
|
6
|
39,5
|
55,0
|
1
|
20
|
Решение
Для построения модели мы
располагаем информацией, представленной в табл. 7.
Таблица 7
Фактические данные для построения модели
|
n
|
y1
|
y2
|
x1
|
x2
|
|
1
|
28,3
|
51,7
|
7
|
12
|
|
2
|
4,4
|
11,5
|
1
|
1
|
|
3
|
33,1
|
64,6
|
10
|
14
|
|
4
|
14,6
|
38,4
|
9
|
4
|
|
5
|
35,9
|
64,1
|
7
|
17
|
|
6
|
39,5
|
55
|
1
|
20
|
|
Сумма
|
155,8
|
285,3
|
35
|
68
|
|
Средн. знач.
|
26,0
|
47,6
|
5,8
|
11,3
|
Структурную модель преобразуем в приведенную форму модели:
y1 = d11x1 + d12x2
+ u1
y2 = d21x1 + d22x2
+ u2
где u1 и u2 — случайные
ошибки.
Для каждого уравнения
приведенной формы при расчете коэффициентов d можно применить МНК.
Для упрощения расчетов можно
работать с отклонениями от средних уровней у = у - уср и х = х - хср
(уср и хср — средние значения). Преобразованные таким
образом данные табл. 7 сведены в табл. 8. Здесь же показаны промежуточные
расчеты, необходимые для определения коэффициентов dlk. Переменные, означающие
отклонение от средних значений, изображаются далее жирным шрифтом и курсивом.
Для нахождения коэффициентов
d1k первого приведенного уравнения
можно использовать следующую систему нормальных уравнений:
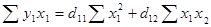
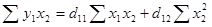
Таблица 8
Преобразованные данные для построения приведенной формы модели
|
n
|
y1
|
y2
|
x1
|
x2
|
y1* x1
|
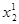
|
x1* x2
|
y1* x2
|
y2* x1
|
y2* x2
|
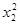
|
|
1
|
2,3
|
4,2
|
1,2
|
0,7
|
2,72
|
1,36
|
0,78
|
1,56
|
4,84
|
2,77
|
0,44
|
|
2
|
-21,6
|
-36,1
|
-4,8
|
-10,3
|
104,24
|
23,36
|
49,94
|
222,86
|
174,24
|
372,52
|
106,78
|
|
3
|
7,1
|
17,1
|
4,2
|
2,7
|
29,72
|
17,36
|
11,11
|
19,02
|
71,04
|
45,47
|
7,11
|
|
4
|
-11,4
|
-9,1
|
3,2
|
-7,3
|
-35,99
|
10,03
|
-23,22
|
83,36
|
-28,98
|
67,10
|
53,78
|
|
5
|
9,9
|
16,6
|
1,2
|
5,7
|
11,59
|
1,36
|
6,61
|
56,29
|
19,31
|
93,78
|
32,11
|
|
6
|
13,5
|
7,5
|
-4,8
|
8,7
|
-65,41
|
23,36
|
-41,89
|
117,29
|
-36,01
|
64,57
|
75,11
|
|
Сумма
|
0,00
|
0,00
|
0,00
|
0,00
|
46,87
|
76,83
|
3,33
|
500,37
|
204,45
|
646,20
|
275,33
|
Подставляя рассчитанные в
табл. 8 значения сумм, получим:
46,87 = 76,83d11
+ 3,33d12;
500,37 = 3,33d11
+ 275,33d12.
Решение этих уравнений дает
значения d11 = 0,53 и d12 = 1,81.
Первое уравнение приведенной
формы модели примет вид:
У1 = 0,53x1
+ 1,81х2+ u1.
Для нахождения коэффициентов
d2k второго приведенного
уравнения можно использовать следующую систему нормальных уравнений:
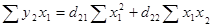
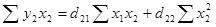
Подставляя рассчитанные в
табл. 8 значения сумм, получим:
204,45 = 76,83d21
+ 3,33d22;
646,20 = 3,33d21
+ 275,33d22.
Решение этих уравнений дает значения d21
= 2,56 и d22= 2,32.
Второе уравнение приведенной формы модели примет
вид:
у2 = 2,56x1 + 2,32x2 + u2.
Для перехода от приведенной
формы к структурной форме модели найдем х2 из второго уравнения
приведенной формы модели:
x2 = (у2 –
2,56х1) / 2,32.
Подставим это выражение в
первое уравнение приведенной модели, найдем структурное уравнение:
y1 = 0,53x1 + 1,81(y2 – 2,56x1) / 2,32 = 0,53x1
+ 0,78у2 – 2,00x1 =
=
0,78у2 – 1,47x1.
Таким образом, b12
= 0,78; а11 = -1,47.
Найдем x1 из
первого уравнения приведенной формы модели:
х1 = (у1
– 1,81x2 ) / 0,53.
Подставим это выражение во второе уравнение
приведенной модели, найдем структурное уравнение:
у2 = 2,32x2
+ 2,56 (у1 – 1,81x2) / 0,53 = 2,32x2 + 4,82y1 – 8,73x2
=
= 4,82y1 — 6,41x2.
Таким образом, b21
= 4,82; а22 = -6,41.
Свободные члены структурной формы находим из
уравнений:
A01 = y1,cp – b12y2,cp – a11x1,cp
= 26,0 – 0,78 • 47,6 – 1,47 • 5,8 = -2,637;
A02
= y2,cp – b21y1,cp – a22x2,cp
= 47,6 – 4,82 • 26,0 – 6,41 • 11,3 = -4,926.
Окончательный вид
структурной модели:
y1 = a01 + b12y2 + a11x1
+ ε1 = -2,637 + 0,782y2 — 1,47x1 + ε1
y2 = a02 + b21y1 + a22x2
+ ε2 = -4,926 + 4,818y1 — 6,41x2 + ε2
[1] Орлова И.В. Экономико-математическое моделирование.
Практическое пособие по решению задач - М.: ВЗФЭИ. Вузовский учебник,
2004.