1 Задача об оптимальном использовании ограниченных ресурсов

Всероссийский заочный финансово-экономический институт

Кафедра Математики и информатики

лабораторная Работа 1, 2

по дисциплине «ЭММ и ПМ»

Уфа

1 Задача об оптимальном использовании ограниченных ресурсов

Небольшая фирма производит два вида продукции: столы и стулья. Для изготовления одного стула требуется 3 м древесины, а для изготовления одного стола – 7 м. На изготовление одного стула уходит 2 часа рабочего времени, а на изготовление стола – 8 часов. Каждый стул приносит 1 ден. ед. прибыли, а каждый стол - 3 ден. ед. Сколько стульев и сколько столов должна изготовить эта фирма для получения максимальной прибыли, если она располагает 200 м древесины и 400 часами рабочего времени?

Экономико-математическая модель задачи

Пусть х₁ – количество столов, которое необходимо изготовить; х₂ – количество стульев, которое необходимо произвести.

Тогда целевая функция будет задаваться следующим образом:

f (x) = 3х₁ + х₂ max.

Ограничения задачи имеют вид:

7х₁ + 3х₂ ≤ 200 – ограничение по сырью;

8х₁ + 2х₂ ≤ 400 – ограничение по труду;

х₁ ≥ 0 – ограничение по столам;

х₂ ≥ 0 − ограничение по стульям.

Решение

1. Создать форму для ввода условий задачи. Запустить Excel, выбрав Microsoft Excel из подменю Программы главного меню Windows. В открывшейся книге на листе 1 создать текстовую форму – таблицу для ввода условий задачи (рис. 1).

2. Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки). Обозначим через х₁, х₂ количество столов и стульев соответственно. В задаче оптимальные значения компонент вектора Х = (х₁, х₂) будут помещены в ячейках В3:C3, оптимальное значение целевой функции – в ячейке D4.

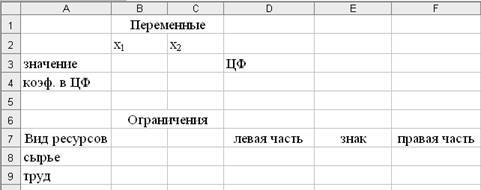
Рис. 1

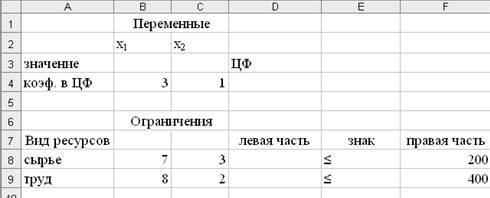
Рис. 2

3. Ввести исходные данные задачи в созданную форму – таблицу, представленную на рис. 2.

4. Сохранить таблицу. Для этого в строке Меню выбрать имя Файл, а в подменю Сохранить как… В появившемся окне выбрать нужную папку для сохранения и в строке Имя файла присвоить имя сохраняемой таблице.

5. Ввести зависимость для целевой функции:

· Поместить курсор в ячейку D4, произойдет выделение ячейки.

· Поместить курсор на кнопку Мастер функций, расположенную на панели инструментов.

· Нажать Enter. На экране появится диалоговое окно Мастер функций шаг 1 из 2.

· В окне Функции выбрать категорию Математические.

· В окне Функции выбрать строку СУММПРОИЗВ (рис. 3). На экране появляется диалоговое окно СУММПРОИЗВ (рис. 4).

· В строку Массив 1 ввести В3:С3.

· В строку Массив 2 ввести В4:С4.

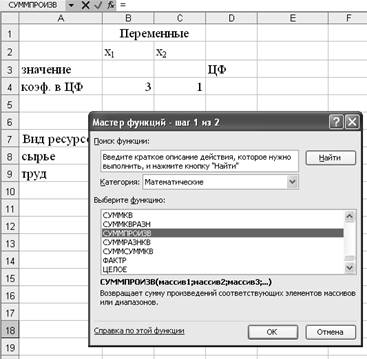
Рис. 3

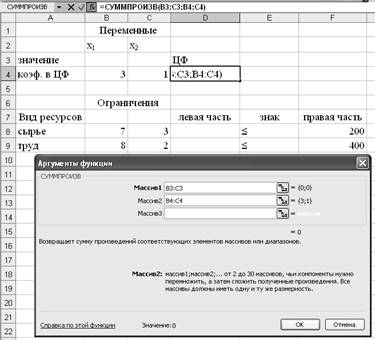
Рис. 4

Массив 1 будет использоваться при вводе зависимостей для ограничений, поэтому на этот массив надо сделать абсолютную ссылку. На рис. 5 показано, что в ячейку D4 введена функция.

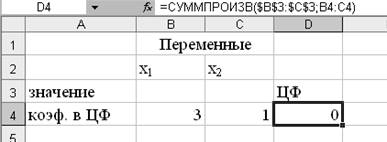
Рис. 5

6. Ввести зависимости для ограничений (рис. 6).

· Поместить курсор в ячейку D4.

· На панели инструментов нажать кнопку Копировать в буфер.

· Поместить курсор в ячейку D8.

· На панели инструментов нажать кнопку Вставить из буфера.

· Поместить курсор в ячейку D9.

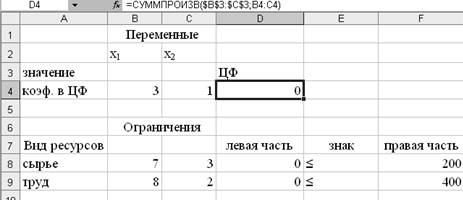
Рис. 6

· На панели инструментов нажать кнопку Вставить из буфера. Содержимое ячеек D4, D8, D9 необходимо проверить. Они обязательно должны содержать информацию, как это показано на рис. 7.

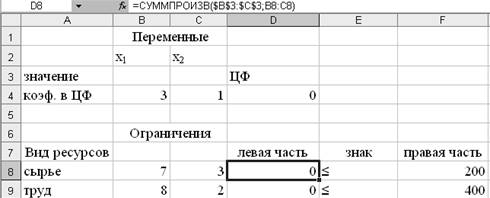
Рис. 7

· В меню Сервис выбрать команду Поиск решения. Появляется диалоговое окно Поиск решения (рис. 8).

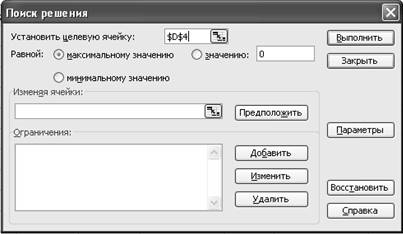
Рис. 8

7. Запустить команду Поиск решения.

8. Назначить ячейку для целевой функции (установить целевую ячейку), указать адреса изменяемых ячеек.

· Поместить курсор в строку Установить целевую ячейку.

· Ввести адрес ячейки $D$4.

· Внести тип целевой функции в зависимости от условия задачи. Для этого отметим, чему равна целевая функция – Максимальному значению.

· Поместить курсор в строку Изменяя ячейки.

· Ввести адреса искомых переменных $В3:$С3 (рис. 9).

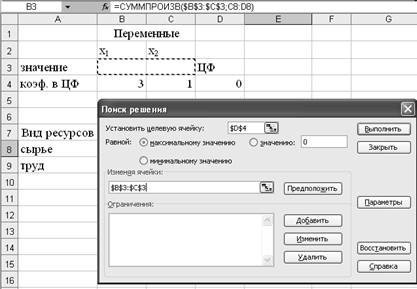
Рис. 9

9. Ввести ограничения.

· Поместить указатель мыши на кнопку Добавить. Появляется диалоговое окно Добавление ограничения.

· В строке Ссылка на ячейку ввести адрес $D$8.

· Ввести знак ограничения.

· В строке Ограничения ввести адрес $F$8 (рис. 10).

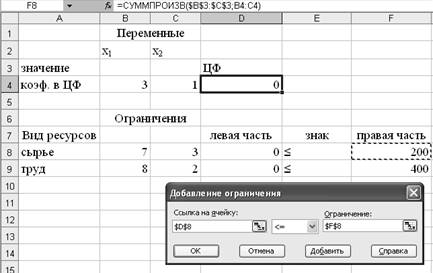
Рис. 10

· Поместить указатель мыши на кнопку Добавить. На экране появится диалоговое окно Добавление ограничения.

· В строке Ссылка на ячейку ввести адрес $D$9.

· Ввести знак ограничения.

· В строке Ограничения ввести адрес $F$9 (рис. 11).

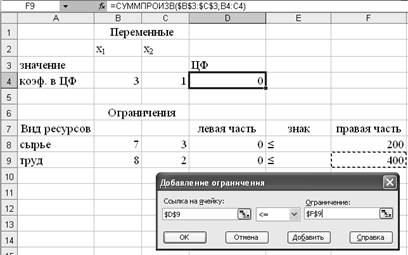
Рис. 11

· Поместить указатель мыши на кнопку Добавить. На экране появится диалоговое окно Добавление ограничения.

· В строке Ссылка на ячейку ввести адрес $B3$C3.

· Вместо знака выбираем выражение «цел».

· После введения последнего ограничения нажать на кнопку ОК.

· На экране появится диалоговое окно Поиск решения с введенными условиями (рис. 12).

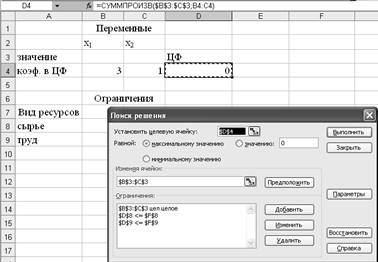
Рис. 12

10. Ввести параметры для решения задачи линейного программирования.

· В диалоговом окне поместить указатель мышки на кнопку Параметры. На экране появится диалоговое окно Параметры поиска решения (рис. 13).

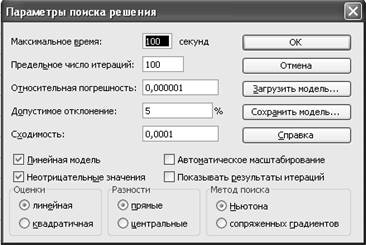
Рис. 13

· Установить флажки в окнах Линейная модель и неотрицательные значения.

· Поместить указатель мыши на кнопку ОК. На экране появится диалоговое окно Поиск решения.

· Поместить указатель мыши на кнопку Выполнить.

Через непродолжительное время появятся диалоговое окно Результаты поиска решения и исходная таблица с заполненными ячейками В3:С3 для значений х₁, х₂ и ячейка D4 с максимальным значением целевой функции (рис. 14).

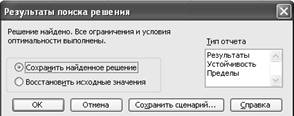
Рис. 14

Вывод: полученное решение задачи об оптимальном использовании ограниченных ресурсов означает, что максимальный доход 85 ден. ед. фирма может получить при выпуске и реализации 28 столов и 1 стула. При этом трудовые ресурсы и сырье будет использовано не полностью: 226 ч из 400 ч и 199 м из 200 м соответственно.

2 Задача о назначениях

Мастер должен назначить на 10 типовых операций 12 рабочих. Данные о времени, которое затрачивают рабочие на выполнение каждой операции, приведены ниже в таблице (матрица эффективностей назначений)

Операции Рабочие	О₁	О₂	О₃	О₄	О₅	О₆	О₇	О₈	О₉	О₁₀
Р₁	29	31	16	16	17	34	20	28	16	13
Р₂	29	25	22	30	24	31	37	23	16	27
Р₃	27	32	-	14	34	30	27	16	19	17
Р₄	21	35	-	32	31	28	30	29	31	16
Р₅	21	36	-	14	24	30	21	28	29	27
Р₆	28	35	25	30	22	16	-	18	25	18
Р₇	27	34	33	26	14	19	18	37	19	16
Р₈	27	34	27	30	37	37	26	22	35	33
Р₉	16	26	18	26	16	20	31	34	28	29
Р₁₀	16	22	33	22	21	19	19	37	36	24
Р₁₁	26	35	13	14	17	36	17	17	25	21
Р₁₂	34	25	19	14	36	36	17	36	26	33

В матрице эффективностей назначений проставлен запрет «-», если рабочий не может выполнять соответствующую операцию.

Сформировать план назначений рабочих по операциям, при котором суммарное время на выполнение работ будет минимально.

Экономико-математическая модель задачи

Пусть х_ij – число рабочих i, назначенных на выполнение операции j.

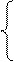
х_ij = 0, если рабочий i не назначен на выполнение операции j,

1, если рабочий i назначен на выполнение операции j.

Тогда целевая функция задается следующим соотношением:

f (x) = х₁₁ + х₂₁ + х₃₁ + х₄₁ + х₅₁ + х₆₁ + х₇₁ + х₈₁ + х₉₁ + х₁₀₁ + х₁₁₁ + х₁₂₁ + х₁₂ + х₂₂ + х₃₂ + х₄₂ + х₅₂ + х₆₂ + х₇₂ + х₈₂ + х₉₂ + х₁₀₂ + х₁₁₂ + х₁₂₂ + х₁₃ + х₂₃ + х₃₃ + х₄₃ + х₅₃ + х₆₃ + х₇₃ + х₈₃ + х₉₃ + х₁₀₃ + х₁₁₃ + х₁₂₃ + х₁₄ + х₂₄ + х₃₄ + х₄₄ + х₅₄ + х₆₄ + х₇₄ + х₈₄ + х₉₄ + х₁₀₄ + х₁₁₄ + х₁₂₄ + х₁₅ + х₂₅ + х₃₅ + х₄₅ + х₅₅ + х₆₅ + х₇₅ + х₈₅ + х₉₅ + х₁₀₅ + х₁₁₅ + х₁₂₅ + х₁₆ + х₂₆ + х₃₆ + х₄₆ + х₅₆ + х₆₆ + х₇₆ + х₈₆ + х₉₆ + х₁₀₆ + х₁₁₆ + х₁₂₆ + х₁₇ + х₂₇ + х₃₇ + х₄₇ + х₅₇ + х₆₇ + х₇₇ + х₈₇ + х₉₇ + х₁₀₇ + х₁₁₇ + х₁₂₇ + х₁₈ + х₂₈ + х₃₈ + х₄₈ + х₅₈ + х₆₈ + х₇₈ + х₈₈ + х₉₈ + х₁₀₈ + х₁₁₈ + х₁₂₈ + х₁₉ + х₂₉ + х₃₉ + х₄₉ + х₅₉ + х₆₉ + х₇₉ + х₈₉ + х₉₉ + х₁₀₉ + х₁₁₉ + х₁₂₉ + х₁₁₀ + х₂₁₀ + х₃₁₀ + х₄₁₀ + х₅₁₀ + х₆₁₀ + х₇₁₀ + х₈₁₀ + х₉₁₀ + х₁₀₁₀ + х₁₁₁₀ + х₁₂₁₀ min.

Ограничения задачи имеют вид:

х₁₁ + х₂₁ + х₃₁ + х₄₁ + х₅₁ + х₆₁ + х₇₁ + х₈₁ + х₉₁ + х₁₀₁ + х₁₁₁ + х₁₂₁ ≤ 1

х₁₂ + х₂₂ + х₃₂ + х₄₂ + х₅₂ + х₆₂ + х₇₂ + х₈₂ + х₉₂ + х₁₀₂ + х₁₁₂ + х₁₂₂ ≤ 1

х₁₃ + х₂₃ + х₃₃ + х₄₃ + х₅₃ + х₆₃ + х₇₃ + х₈₃ + х₉₃ + х₁₀₃ + х₁₁₃ + х₁₂₃ ≤ 1

х₁₄ + х₂₄ + х₃₄ + х₄₄ + х₅₄ + х₆₄ + х₇₄ + х₈₄ + х₉₄ + х₁₀₄ + х₁₁₄ + х₁₂₄ ≤ 1

х₁₅ + х₂₅ + х₃₅ + х₄₅ + х₅₅ + х₆₅ + х₇₅ + х₈₅ + х₉₅ + х₁₀₅ + х₁₁₅ + х₁₂₅ ≤ 1

х₁₆ + х₂₆ + х₃₆ + х₄₆ + х₅₆ + х₆₆ + х₇₆ + х₈₆ + х₉₆ + х₁₀₆ + х₁₁₆ + х₁₂₆ ≤ 1

х₁₇ + х₂₇ + х₃₇ + х₄₇ + х₅₇ + х₆₇ + х₇₇ + х₈₇ + х₉₇ + х₁₀₇ + х₁₁₇ + х₁₂₇ ≤ 1

х₁₈ + х₂₈ + х₃₈ + х₄₈ + х₅₈ + х₆₈ + х₇₈ + х₈₈ + х₉₈ + х₁₀₈ + х₁₁₈ + х₁₂₈ ≤ 1

х₁₉ + х₂₉ + х₃₉ + х₄₉ + х₅₉ + х₆₉ + х₇₉ + х₈₉ + х₉₉ + х₁₀₉ + х₁₁₉ + х₁₂₉ ≤ 1

х₁₁₀ + х₂₁₀ + х₃₁₀ + х₄₁₀ + х₅₁₀ + х₆₁₀ + х₇₁₀ + х₈₁₀ + х₉₁₀ + х₁₀₁₀ + х₁₁₁₀ + х₁₂₁₀ ≤ 1

х_ij = 0, i = 1, 2,…, n

1. j = 1, 2,…, m.

Решение

1. Создать форму для решения задачи (матрица эффективностей назначений). Для этого необходимо выполнить резервирование изменяемых ячеек: в блок ячеек В3:К14 вводятся «1». Таким образом, резервируется место, где после решения задачи будет находиться распределение по операциям, обеспечивающих выполнение работ за минимальное время.

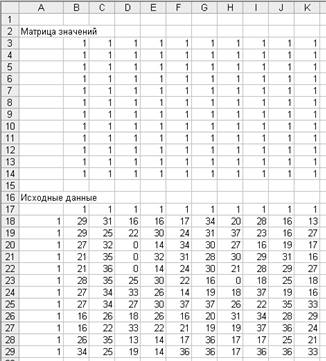
Рис. 15

2. Ввод ограничений условий.

· Поместить курсор в ячейку А3 и щелкнуть знак «∑».

· Выделить необходимые для суммирования ячейки В3:К3 и нажать Enter.

· Аналогичные действия выполнить для ячеек А4-А14. Для этого поместить курсор в А3 и на панели инструментов нажать кнопку Копировать в буфер. Далее выделить ячейки А4-А14 и нажать кнопку Вставить из буфера.

· Ввести условия заполнения матрицы назначений. Для этого необходимо поместить курсор В15 и щелкнуть значок «∑», при этом автоматически выделяется столбец В3:В14. Нажать Enter.

· Аналогичным образом заполнить ячейки С15:К15. Сделать это можно следующим образом: встать на ячейку В15, на панели инструментов нажать кнопку Копировать в буфер, выделить ячейки С15:К15 и нажать кнопку Вставить из буфера.

3. Назначение целевой функции.

· Поместить курсор в ячейку В31, произойдет выделение ячейки.

· Поместить курсор на кнопку Мастер функций, расположенную на панели инструментов.

· Нажать Enter. На экране появится диалоговое окно Мастер функций шаг 1 из 2.

· В окне Функции выбрать категорию Математические.

· В окне Функции выбрать строку СУММПРОИЗВ. На экране появляется диалоговое окно СУММПРОИЗВ.

· В строку Массив 1 ввести В18:В29.

· В строку Массив 2 ввести В3:К14 (рис. 16).

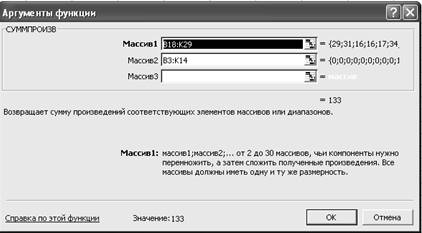
Рис. 16

В поле В31 появится некоторое числовое значение, равное произведению единичных поставок на удельные коэффициенты затрат по доставке грузов (рис. 17).

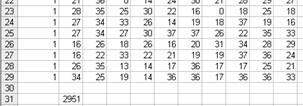
Рис. 17

4. Ввод зависимостей из математической модели (рис. 18).

· В меню Сервис выбрать команду Поиск решения.

· В открывшемся окне в поле установить целевую ячейку ввести адрес $В$31.

· Установить направление изменения целевой функции, равное «минимальному значению».

· Ввести адреса изменяемых ячеек В3:К14.

· Ввести ограничения задачи. Для этого нужно щелкнуть на кнопку Добавить. В поле Ссылка на ячейку ввести адреса $А$3:$А$14, в среднем поле установить знак «≤», а поле Ограничение установить адреса $А$18:$А$29. Нажать ОК.

· Для ввода следующего ограничения опять нажать кнопку Добавить. В поле Ссылка на ячейку ввести адреса $В$15:$К$15, в среднем поле установить знак «=», а поле Ограничение установить адреса $В$17:$К$17. Нажать ОК.

· Здесь же необходимо учесть, что при решении задач о назначении в Excel необходимо учитывать, что переменные x_ij являются булевыми. Следовательно необходимо ввести еще одно ограничение. Нажать кнопку Добавить. В поле Ссылка на ячейку ввести адреса $В$3:$К$14, в среднем поле установить значение «двоич». Нажать ОК.

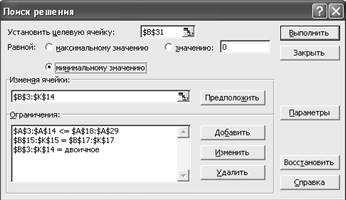
Рис. 18

5. Ввод ограничений

· Установить флажки в окнах Линейная модель и неотрицательные значения.

· Поместить указатель мыши на кнопку ОК. На экране появится диалоговое окно Поиск решения.

· Поместить указатель мыши на кнопку Выполнить.

Рис. 19

6. После выполнения всех вышеуказанных действий на экран выводится окно результаты поиска решения (рис. 14). В окне Тип отчета выбрать интересующий вид отчета. Нажать ОК.

Вывод: минимальное суммарное время на выполнение работ было достигнуто при назначении:

· Первого работника на операцию О₁₀ (ячейка К3);

· Второго работника на операцию О₉ (ячейка J4);

· Третьего работника на операцию О₈ (ячейка I5);

· Четвертого работника ни на какую операцию;

· Пятого работника на операцию О₄ (ячейка Е7);

· Шестого работника на операцию О₆ (ячейка G8);

· Седьмого работника на операцию О₅ (ячейка F9);

· Восьмого работника ни на какую операцию;

· Девятого работника на операцию О₁ (ячейка В11);

· Десятого работника на операцию О₂ (ячейка С12);

· Одиннадцатого работника на операцию О₃ (ячейка D13);

· Двенадцатого работника на операцию О₇ (ячейка Н14).

3 Транспортная задача

Необходимо решить транспортную задачу – минимизировать расходы на доставку продукции со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объем заказа и количество продукции, хранящейся на складе.

Таблица тарифов на перевозку продукции и объемов запасов на складе и заказов:

Магазин Склад	«Колбасы»	«Мясо»	«Мясные деликатесы»	«Дина»	Запасы на складе (ед. продукции)
Черкизово	1	0	0,5	2	45
Царицыно	3	2	4	1	50
Бородино	0	2,5	2	3	15
Вешняки	4	3	1,5	2	20
Объем заказа (ед. продукции)	30	40	20	25

Экономико-математическая модель задачи

Задача является открытой, т.к. объем заказа меньше запасов на складе. Пусть х_ij – количество единиц продукции, которое нужно перевести с i-ого склада в j-ый магазин.

Тогда целевая функция имеет следующий вид:

f (x) = х₁₁ + 3х₂₁ + 4х₄₁ + 2х₂₂ + 2,5х₃₂ + 3х₄₂ + 0,5х₁₃ + 4х₂₃ + 2х₃₃ +1,5 х₄₃ + 2х₁₄ + х₂₄ + 3х₃₄ + 2х₄₄ min.

Ограничения задачи задаются так:

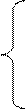х₁₁ + 3х₂₁ + 4х₄₁ = 30,

2х₂₂ + 2,5х₃₂ + 3х₄₂ = 40,

0,5х₁₃ + 4х₂₃ + 2х₃₃ + 1,5х₄₃ = 20,

2х₁₄ + х₂₄ + 3х₃₄ + 2х₄₄ = 25.

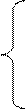х₁₁ + 0,5х₁₃ + 2х₁₄ ≤ 45,

3х₂₁ + 2х₂₂ + 4х₂₃ + х₂₄ ≤ 50,

2,5х₃₂ + 2х₃₃ + 3х₃₄ ≤ 15,

4х₄₁ + 3х₄₂ + 1,5х₄₃ + 2х₄₄ ≤ 20.

х_ij ≥ 0, i = 1, 2,…, n j = 1, 2,…, m

Решение

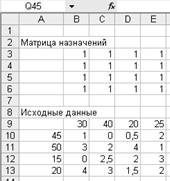
Рис. 20

2. Ввод ограничений условий.

· Поместить курсор в ячейку А3 и щелкнуть знак «∑».

· Выделить необходимые для суммирования ячейки В3:Е3 и нажать Enter.

· Аналогичные действия выполнить для ячеек А4-А6. Для этого поместить курсор в А3 и на панели инструментов нажать кнопку Копировать в буфер. Далее выделить ячейки А4-А6 и нажать кнопку Вставить из буфера.

· Ввести условия заполнения матрицы назначений. Для этого необходимо поместить курсор В7 и щелкнуть значок «∑», при этом автоматически выделяется столбец В3:В6. Нажать Enter.

· Аналогичным образом заполнить ячейки С7:Е7. Сделать это можно следующим образом: встать на ячейку В15, на панели инструментов нажать кнопку Копировать в буфер, выделить ячейки С7:Е7 и нажать кнопку Вставить из буфера.

3. Назначение целевой функции.

· Поместить курсор в ячейку В15, произойдет выделение ячейки.

· Поместить курсор на кнопку Мастер функций, расположенную на панели инструментов.

· Нажать Enter. На экране появится диалоговое окно Мастер функций шаг 1 из 2.

· В окне Функции выбрать категорию Математические.

· В окне Функции выбрать строку СУММПРОИЗВ. На экране появляется диалоговое окно СУММПРОИЗВ.

· В строку Массив 1 ввести В10:Е13.

· В строку Массив 2 ввести В3:Е6 (рис. 21).

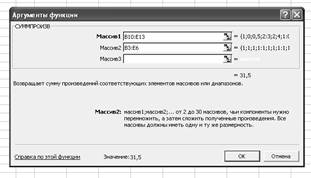
Рис. 21

В поле В15 появится некоторое числовое значение, равное произведению единичных поставок на удельные коэффициенты затрат по доставке грузов (рис. 22).

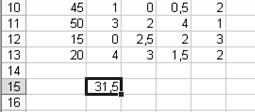
Рис. 22

4. Ввод зависимостей из математической модели (рис. 23).

· В меню Сервис выбрать команду Поиск решения.

· В открывшемся окне в поле установить целевую ячейку ввести адрес $В$15.

· Установить направление изменения целевой функции, равное «минимальному значению».

· Ввести адреса изменяемых ячеек В3:Е6.

· Ввести ограничения задачи. Для этого нужно щелкнуть на кнопку Добавить. В поле Ссылка на ячейку ввести адреса $А$3:$А$6, в среднем поле установить знак «≤», а поле Ограничение установить адреса $А$10:$А$13. Нажать ОК.

· Для ввода следующего ограничения опять нажать кнопку Добавить. В поле Ссылка на ячейку ввести адреса $В$7:$Е$7, в среднем поле установить знак «=», а поле Ограничение установить адреса $В$9:$Е$9. Нажать ОК.

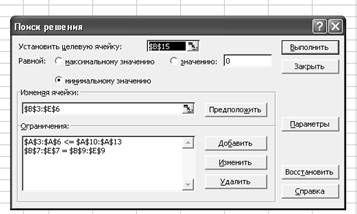
Рис. 23

5. Ввод ограничений

· Установить флажки в окнах Линейная модель и неотрицательные значения.

· Поместить указатель мыши на кнопку ОК. На экране появится диалоговое окно Поиск решения.

· Поместить указатель мыши на кнопку Выполнить.

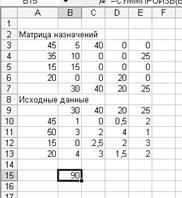
Рис. 20

Вывод: минимум затрат на доставку продукции, равный 90 ден. ед., будет обеспечен при следующем плане поставок:

· Со склада Черкизово в магазин «Колбасы» в объеме 5 единиц и магазин «Мясо» в объеме 40 единиц;

· Со склада Царицыно в магазин «Колбасы» в объеме 10 единиц и магазин «Дина» в объеме 25 единиц;

· Со склада Бородино в магазин «Колбасы» в объеме 15 единиц;

· Со склада Вешняки в магазин «Мясные деликатесы» в объеме 20 единиц.