Задача 1

Задача линейного программирования

Задача. Фирма выпускает два вида древесно-стружечных плит - обычные и улучшенные. При этом производятся две основные операции - прессование и отделка. Определите, какое количество плит каждого типа следует изготовить в течение месяца так, чтобы обеспечить максимальную прибыль при следующих ограничениях на ресурсы (материал, время, средства), указанных в таблице 1.

Таблица 1

Затраты	Партия из 100 плит	Имеющиеся ресурсы на месяц
обычных	улучшенных
Материал, кг	20	40	4000
Время на прессование, ч	4	6	900
Время на отделку, ч	4	4	600
Средства, ден. ед.	30	50	6000

Известно, что за каждые 100 обычных плит фирма получает прибыль, равную 80 ден. ед., а за каждые 100 плит улучшенного вида - 100 ден. ед.

Экономико-математическая модель задачи

Обозначим через х₁ – число партий, каждая из которых состоит из 100 обычных плит, х₂ – число партий, каждая из которых состоит из 100 улучшенных плит (количество плит каждого типа, умноженные на 100).

Целевая функция - это математическая запись критерия оптимальности, т.е. выражение, которое необходимо максимизировать:

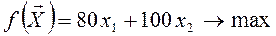
Ограничения по затратам:

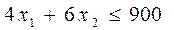
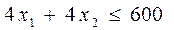
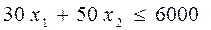
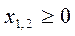
Решение ЗЛП с помощью команды Поиск решения в среде MS Excel

Приведем описание технологии получения решения приведенной ЗЛП.

1. Запустить Excel, выбрав Microsoft Excel из подменю Программы главного меню Windows. Открывается чистый лист Excel. Создать текстовую форму - таблицу для ввода условий задачи (рис. 1.1).

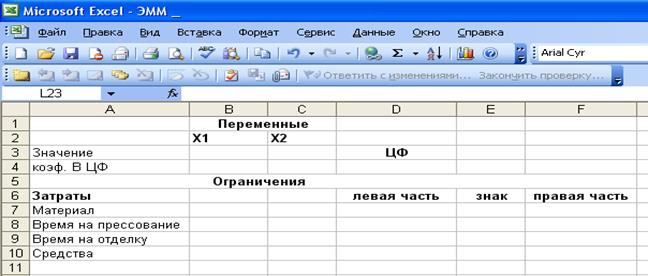
Рис. 1.1

2. Укажем адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки). Обозначим через х₁, х₂ - число партий, каждая из которых состоит из 100 обычных и улучшенных плит соответственно (количество плит каждого типа, умноженные на 100). В нашей задаче оптимальные значения вектора 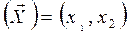будут помещены в ячейках ВЗ:С3, оптимальное значение целевой функции - в ячейке D4.

3. Ввести исходные данные задачи в созданную форму-таблицу, представленную на рис. 1.2.

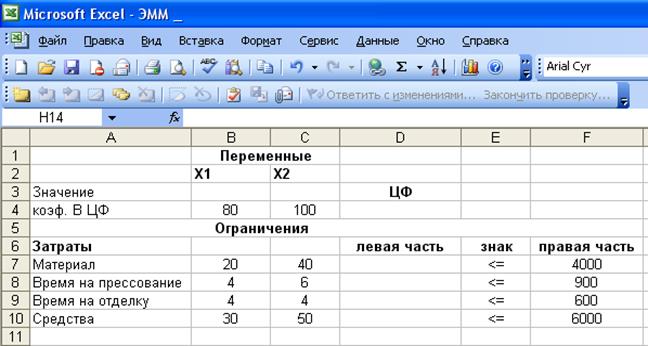
Рис. 1.2

4. Ввести зависимость для целевой функции:

• установить курсор в ячейку D4;

• установить курсор на кнопку «Мастер функций», расположенную на панели инструментов. Щелчком левой кнопки мыши открыть «Мастер функций». На экране появляется диалоговое окно Мастер функций шаг 1 из 2. В окне «Категории» выбираем – Математические, в окне «Функции» выбираем – СУММПРОИЗВ (рис. 1.3). → «ОК».

Рис. 1.3

• На экране появляется диалоговое окно СУММПРОИЗВ (рис. 1.4);

• в строку «Массив 1» ввести $В$З:$С$3; адреса ячеек удобнее вводить не с клавиатуры, а протаскивая мышь по указанным ячейкам.

• в строку «Массив 2» ввести В4:С4;

• нажать кнопку «ОК».

На экране с помощью функции СУММПРОИЗВ в ячейку D4 введена функция (рис. 1.4).

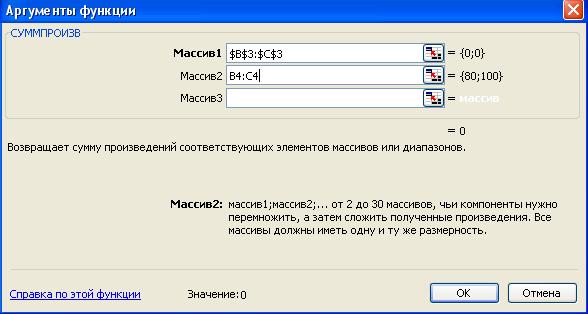
Рис. 1.4

5. Ввести зависимости для ограничений:

• установить курсор в ячейку D4, нажать левую клавишу мыши – откроется контекстное меню, в нем выбрать - копировать;

• установить курсор в ячейку D7, нажать левую клавишу мыши – откроется контекстное меню, в нем выбрать - вставить;

Для ячеек D8, D9, D10 произвести аналогичные ячейке D7 операции.

В результате данных преобразований исходная таблица принимает вид, представленный на рисунке 1.5.

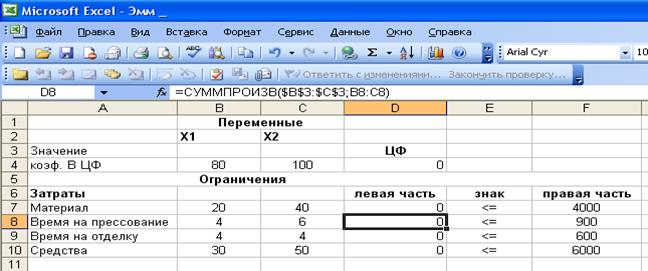
Рис. 1.5

Проверить введенные формулы. На панели инструментов выбрать Сервис→ Зависимости формул → Режим проверки формул (рис. 1.6)

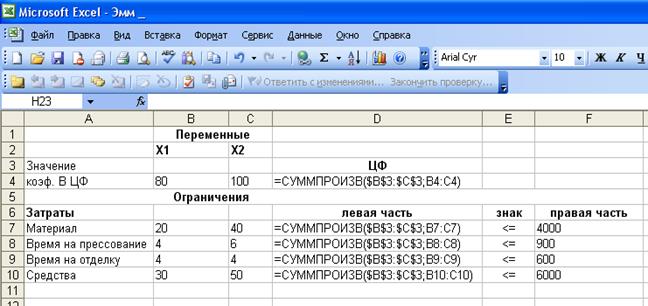
Рис. 1.6

6. Запустить команду Поиск решения.

На панели инструментов выбрать Сервис→ команда Поиск решения → ОК. Появляется диалоговое окно Поиск решения (рис. 1.7).

7. Назначить ячейку для целевой функции:

• установить курсор в строку Установить целевую ячейку;

• ввести адрес ячейки $D$4, щелкнув по соответствующей ячейке рабочего листа;

• ввести направление целевой функции. В нашей задаче целевая функция равна максимальному значению;

• установить курсор в строку Изменяя ячейки;

• ввести адреса искомых переменных В$3:С$3 (рис. 1.7).

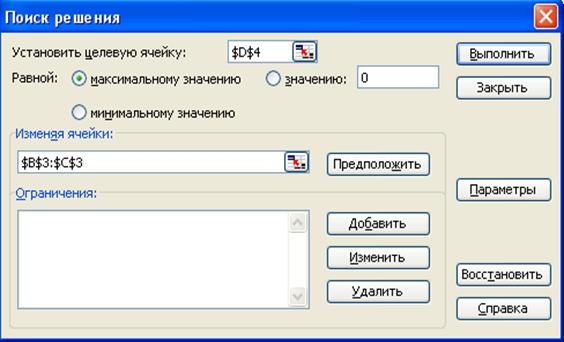
Рис. 1.7

8. Ввести ограничения:

• установить указатель мыши на кнопку Добавить и щелкнуть мышью по ней. Появляется диалоговое окно Добавление ограничения (рис. 1.8);

• в строке Ссылка на ячейку ввести адрес $D$7;

• ввести знак ограничения <=;

• в строке Ограничение ввести адрес $F$7;

• установить указатель мыши на кнопку Добавить и щелкнуть мышью по ней. На экране вновь появляется диалоговое окно Добавление ограничения (рис. 1.8).

• ввести остальные ограничения задачи, по вышеописанному алгоритму;

• после введения последнего ограничения нажать кнопку ОК.

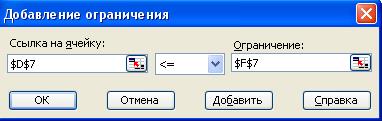
Рис. 1.8

На экране появится диалоговое окно Поиск решения с введенными условиями (рис. 1.9).

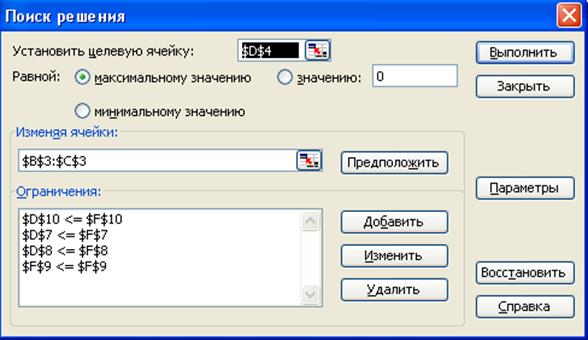
Рис. 1.9

9. Ввести параметры для решения ЗЛП:

• в диалоговом окне Поиск решения установить указатель мыши на кнопку Параметры и щелкнуть мышью по ней. На экране появляется диалоговое окно Параметры поиска решения (рис. 1.10);

• установить флажки в окнах Линейная модель (это обеспечит применение симплекс-метода) и Неотрицательные значения (рис. 1.10);

• нажать кнопку ОК.

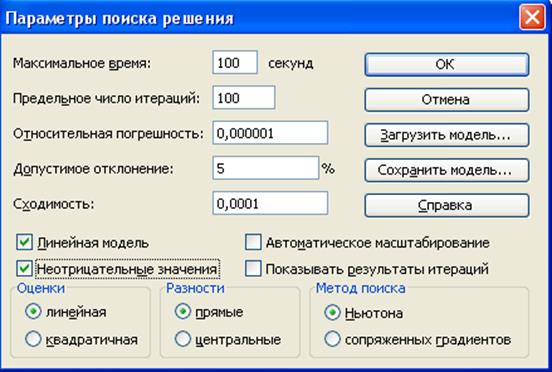
Рис. 1.10

На экране опять появляется диалоговое окно Поиск решения;

• установить указатель мыши на кнопку Выполнить.

Через непродолжительное время появляется диалоговое окно Результаты поиска решения (рис 1.11) и исходная таблица с заполненными ячейками ВЗ:С3, в которых указываются максимальные в соответствии со значением целевой функции значения х₁, х₂, и ячейкой D4, в которой указывается максимальное значение целевой функции (рис. 1.12).

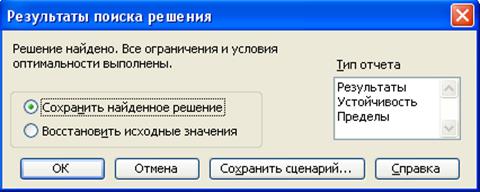
Рис. 1.11

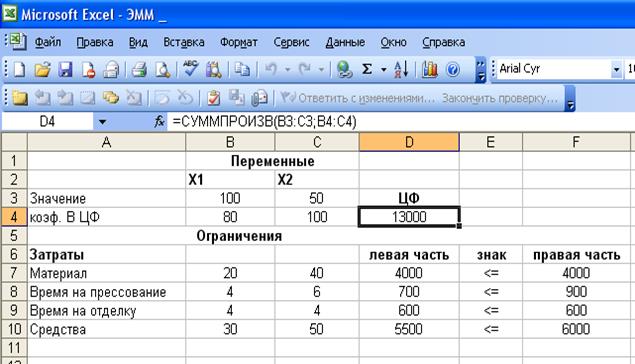
Рис. 1.12

10. Создать отчеты по результатам, устойчивости и пределам.

• В окне Результаты поиска решения в поле тип отчета выбрать – Результаты → ОК. Создается отчет по результатам (рис. 1.13)

В отчет по результатам включаются исходные и конечные значения целевой и изменяемых ячеек, дополнительные сведения об ограничениях.

• Запустить команду Поиск решения→ Выполнить→ тип отчета – Устойчивость → ОК. Создается отчет по устойчивости (рис. 1.14)

В отчете по устойчивости показывается насколько чувствительно решение к изменениям коэффициентов целевой функции или правых частей ограничений. Для линейных моделей отчет включает нормируемую стоимость, теневые цены и ограничения на изменение правой части равенства.

• Запустить команду Поиск решения→ Выполнить→ тип отчета – Пределы → ОК. Создается отчет по пределам (рис. 1.15)

В отчете по пределам показываются изменяемые и целевая ячейки вместе с соответствующими значениями, верхние и нижние пределы и целевые значения.

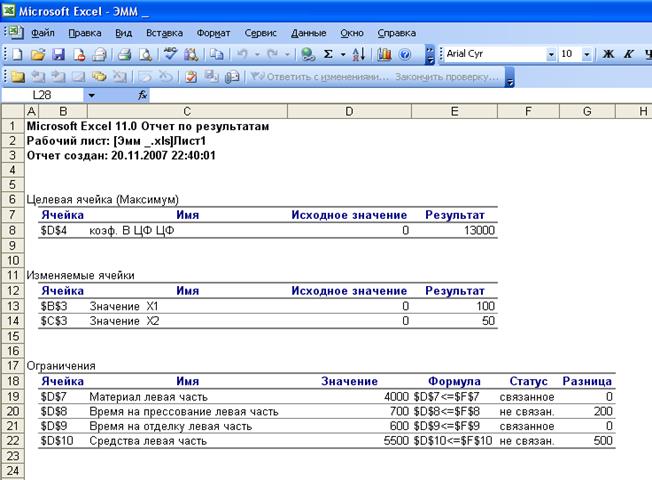
Рис. 1.13

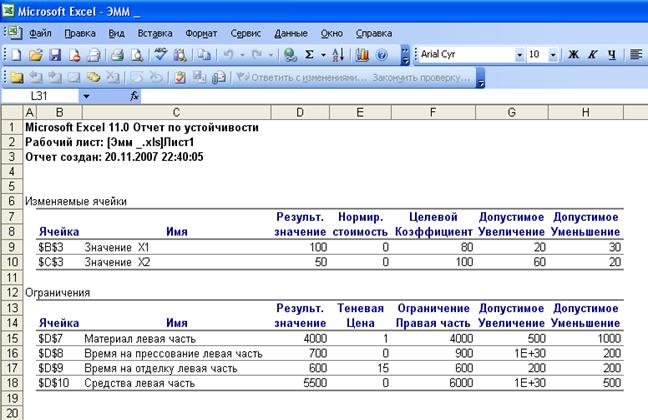
Рис. 1.14

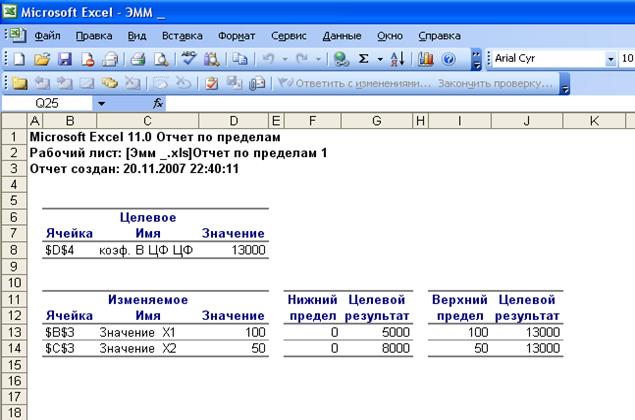
Рис. 1.15

Вывод:

Полученное решение означает, что необходимо в течение месяца изготовить 100 партий обычных плит или 10000 обычных плит, и 50 партий улучшенных плит или 5000 улучшенных плит, что бы обеспечить максимальную прибыль, равную 13000 денежных единиц. При этом материал и время на отделку будут использованы полностью (см. рис. 1.13), а из времени на прессование, равного 900 часов, будет использовано 700 часов, из средств на выполнение работы в размере 6000 денежных единиц будет использовано 5500 денежных единиц. Следователь, 200 часов на прессование и 500 денежных единиц, из имеющихся ресурсов на месяц, для изготовления плит не используются.