Задача 1. Цех мебельного комбината выпускает трельяжи, трюмо и тумбочки под телевизоры. Норма расхода материалов в расчете на одно изделие, плановая себестоимость, оптовая цена предприятия, плановый ассортимент и трудоемкость продукции приведены в таблице. При этом запас древесно-стружечных плит, досок еловых и березовых 90, 30 и 14 м³ соответственно. Плановый фонд рабочего времени 16800 чел./час.

Показатели	Изделия
трельяж	трюмо	тумбочка
Норма расхода материала, м3: древесностружечные плиты	0,032	0,031	0,038
Доски еловые	0,020	0,020	0,008
Доски березовые	0,005	0,005	0,006
Трудоемкость, чел./час	10,2	7,5	5,8
Плановая себестоимость, у.е.	88,81	63,98	29,60
Оптовая цена предприятия, у.е.	93,00	67,00	30,00
Плановый ассортимент, шт	350	290	1200

Исходя из необходимости выполнить план по ассортименту и возможности его перевыполнения по отдельным (и даже всем) показателям построить модель, на основе которой можно найти план производства, максимизирующий прибыль.

1.                          Как изменится план выпуска при увеличении запаса досок еловых на 5м³?

2.                          К чему приведет увеличение плана выпуска по тумбочкам на 100 штук?

Решение

Экономико-математическая модель:

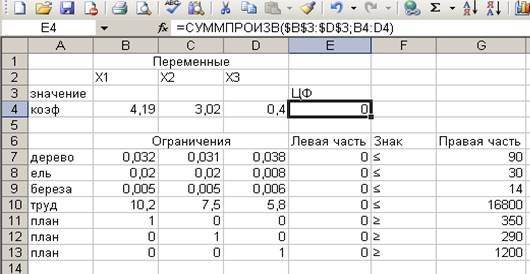
Целевая функция:

4,19*Х1+3,02*Х2+0,4*Х3→max

Ограничения:

0,032*Х1+0,031*Х2+0,038*Х3≤90

0,020*Х1+0,020*Х2+0,008*Х3≤30

0,005*Х1+0,05*Х2+0,006*Х3≤14

10,2*Х1+7,5*Х2+5,8*Х3≤16800

Х1≥350

Х2≥290

Х3≥1200

Х1, Х2, Х3 – целое.

Х1 – количество трельяжей, Х2 – количество трюмо, Х3 – количество тумбочек.

Введем исходные данные задачи.

Введем все ограничения

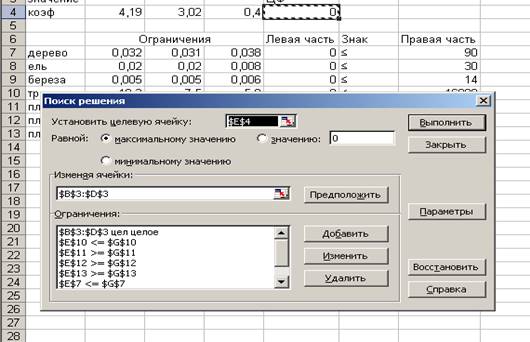
Решение найдено

	Переменные
	Х1	Х2	Х3
значение	730	290	1200	ЦФ
коэф	4,19	3,02	0,4	4414,5
	Ограничения	Левая часть	Знак	Правая часть
дерево	0,032	0,031	0,038	77,95	≤	90
ель	0,02	0,02	0,008	30	≤	30
береза	0,005	0,005	0,006	12,3	≤	14
труд	10,2	7,5	5,8	16581	≤	16800
план	1	0	0	730	≥	350
план	0	1	0	290	≥	290
план	0	0	1	1200	≥	1200

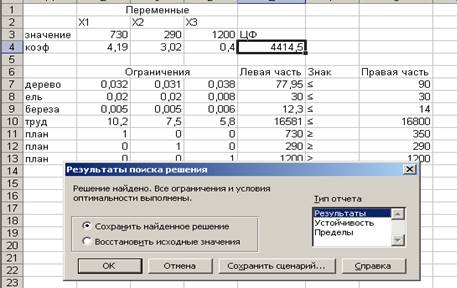
Таким образом, необходимо выпустить 730 трельяжей, 290 трюмо и 1200 тумбочек. Прибыль составит 4414,5 у.е

Если запас еловых досок увеличить на 5м³, то мы получим следующее решение:

	Переменные
	Х1	Х2	Х3
значение	750	292	1200	ЦФ
коэф	4,19	3,02	0,4	4504,34
	Ограничения	Левая часть	Знак	Правая часть
дерево	0,032	0,031	0,038	78,652	≤	90
ель	0,02	0,02	0,008	30,44	≤	35
береза	0,005	0,005	0,006	12,41	≤	14
труд	10,2	7,5	5,8	16800	≤	16800
план	1	0	0	750	≥	350
план	0	1	0	292	≥	290
план	0	0	1	1200	≥	1200

Прибыль при этом увеличится до 4504,34 у.е.

Если план выпуска по тумбочкам увеличить на 100, то получим:

	Переменные
	Х1	Х2	Х3
значение	690	290	1300	ЦФ
коэф	4,19	3,02	0,4	4286,9
	Ограничения	Левая часть	Знак	Правая часть
дерево	0,032	0,031	0,038	80,47	≤	90
ель	0,02	0,02	0,008	30	≤	30
береза	0,005	0,005	0,006	12,7	≤	14
труд	10,2	7,5	5,8	16753	≤	16800
план	1	0	0	690	≥	350
план	0	1	0	290	≥	290
план	0	0	1	1300	≥	1300

Прибыль уменьшится до 4286,9 у.е.

Задача 2. Фирма обслуживает 5 клиентов. Каждый день она доставляет им товары на грузовых машинах. Существует три допустимых маршрута доставки, каждый из которых позволяет обслужить определенное количество клиентов и требует использования в течение дня одного транспортного средства. Каждый маршрут характеризуется определенными расходами (см. таблицу).

Клиенты	Маршруты
1	2	3
1	1		1
2	1
3	1		1
4		1
5		1	1
Расходы по маршруту	900	1000	800

Необходимо выбрать такое множество маршрутов, при котором обеспечивается обслуживание каждого клиента и, кроме того, суммарные расходы минимальны, при условии, что каждый клиент обслуживается один раз в день.

Решение

Составим экономико-математическую модель:

Z=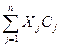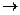min

Систему ограничений получим из следующих условий:

,

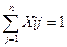Xi-двоичное

Хi – выбранный маршрут

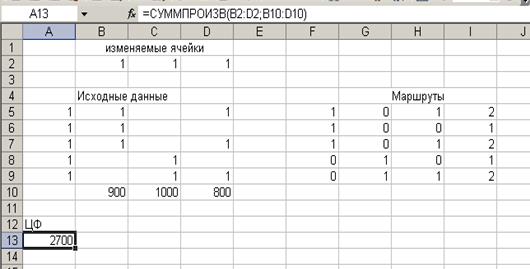
                                     Введены исходные данные

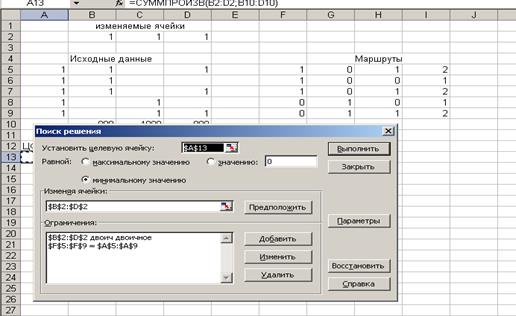
            Введены ограничения

             Решение найдено

	изменяемые ячейки
	1	1	0
	Исходные данные					Маршруты
1	1	0	1		1	1	0	0
1	1	0	0		1	1	0	0
1	1	0	1		1	1	0	0
1	0	1	0		1	0	1	0
1	0	1	1		1	0	1	0
	900	1000	800
ЦФ
1900

Мы видим, что расходы будут минимальны и все условия соблюдены при выборе маршрута 1 и 2. Расходы составят 1900.