Всероссийский заочный
финансово – экономический институт
Контрольная работа
по дисциплине: «Финансовая
математика»
5
Вариант
Выполнила:
Специальность: Финансы и кредит
Курс: 4
Группа: 2
№ зачётки:
Руководитель:
2006г.
Содержание
1. Задание 1…………………………………………………………3
2. Задание 2………………………………………………………..16
3. Задание 3………………………………………………………..23
Задача 3.1………………………………………………….........23
Задача 3.2………………………………………………….........24
Задача 3.3………………………………………………….........25
Задача 3.4………………………………………………….........26
Задача 3.5………………………………………………….........27
Задача 3.6………………………………………………….........28
Задача 3.7………………………………………………….........29
Задача 3.8………………………………………………….........30
Задача 3.9………………………………………………….........31
Задача 3.10……………………………………………………...32
Задание 1.
Имеются
поквартальные данные о кредитах от коммерческого банка на жилищное
строительство (в условных единицах) за 4 года.
Требуется:
1) Построить адаптивную мультипликативную модель Хольта –
Уинтерса с учётом сезонного фактора, приняв параметры сглаживания 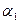 =0,3;
=0,3;  =0,6;
=0,6;
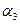 =0,3.
=0,3.
2) Оценить точность
построенной модели с использованием средней относительной ошибки аппроксимации.
3) Оценить
адекватность построенной модели на основе исследования:
- случайности остаточной компоненты
по критерию пиков;
- независимости уровней ряда
остатков по d – критерию 9критические значения d = 1,10 и d = 1,37) и по первому коэффициенту автокорреляции
при критическом значении r1
= 0,32;
- нормальности распределения
остаточной компоненты по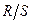 - критерию с
критическими значениями от 3 до 4,21.
- критерию с
критическими значениями от 3 до 4,21.
4) Построить точечный прогноз на 4 шага
вперёд, т.е. на 1 год.
5) Отразить на графике фактические,
расчётные и прогнозные данные.
Решение:
Имеются
поквартальные данные о кредитах, выданных банком.
|
год. кв
|
1
|
2
|
3
|
4
|
|
|
|
1
|
35
|
44
|
52
|
34
|
|
|
2
|
37
|
48
|
59
|
36
|
|
|
3
|
41
|
52
|
62
|
38
|
|
|
4
|
46
|
56
|
67
|
41
|
|
Построение адаптивной мультипликативной
модели Хольта – Уинтерса.
|
t
|
yt
|
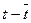
|
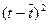
|
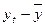
|
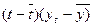
|
y(t)
|
|
|
|
1
|
35
|
-3,5
|
12,25
|
-8,12
|
28,42
|
40,07
|
|
|
2
|
44
|
-2,5
|
6,25
|
0,87
|
-2,2
|
40,94
|
|
|
3
|
52
|
-1,5
|
2,25
|
8,87
|
-13,32
|
41,81
|
|
|
4
|
34
|
-0,5
|
0,25
|
-9,12
|
4,56
|
42,68
|
|
|
5
|
37
|
0,5
|
0,25
|
-6,12
|
-3,06
|
43,55
|
|
|
6
|
48
|
1,5
|
2,25
|
4,87
|
7,32
|
44,42
|
|
|
7
|
59
|
2,5
|
6,25
|
15,87
|
39,7
|
45,29
|
|
|
8
|
36
|
3,5
|
12,25
|
-7,12
|
-24,92
|
46,16
|
|
|
36
|
345
|
0
|
42
|
0,04
|
36,5
|
344,92
|
|
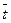 =
= 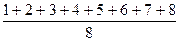 =
= 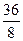 = 4,5
= 4,5
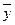 =
= 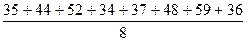 =
= 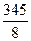 = 43,12
= 43,12
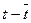 = 1 – 4,5 = -3,5
= 1 – 4,5 = -3,5
2 – 4,5 = -2,5
3 – 4,5 = -1,5
4 – 4,5 = -0,5
5 – 4,5 = 0,5
6 – 4,5 = 1,5
7 – 4,5 = 2,5
8 – 4,5 = 3,5
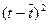 = (-3,5)2 = 12,25
= (-3,5)2 = 12,25
(-2,5)2 = 6,25
(-1,5)2 = 2,25
(-0,5)2 = 0,25
0,52 = 0,25
1,52 = 2,25
2,52 = 6,25
3,52 = 12,25
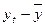 = 35 – 43,12 = -8,12
= 35 – 43,12 = -8,12
44 – 43,12 = 0,88
52 – 43,12 = 8,88
34 – 43,12 = -9,12
37 – 43,12 = -6,12
48 – 43,12 = 4,88
59 – 43,12 = 15,88
36 – 43,12 = -7,12

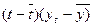 = (-3,5)(-8,12) = 28,42
= (-3,5)(-8,12) = 28,42
(-2,5)∙0,88 = -2,2
(-1,5)∙8,88 = -13,32
(-0,5)(-9,12) = 4,56
0,5∙(-6,12) = -3,06
1,5∙4,88 = 7,32
2,5∙15,88 = 39,7
3,5∙(-7,12) = -24,92
b = 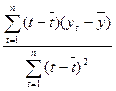
b(0) = 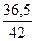 = 0,87
= 0,87
a = 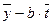
a(0) = 43,12 – 0,87 ∙ 4,5 = 43,12 – 3,915 = 39,20
a(0) = 39,20 – для Тренда
yt = 39,20 + 0,87 = 40,07
40,07 + 0,87 = 40,94
40,94 + 0,87 = 41,81
41,81 + 0,87 = 42,68
42,68 + 0,87 = 43,55
43,55 + 0,87 = 44,42
44,42 + 0,87 = 45,29
45,29 + 0,87 = 46,16
1 КВ.
F(-3) = 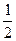 ∙(
∙(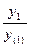 +
+ 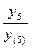 ) =
) = 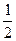 ∙(
∙(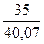 +
+ 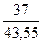 ) =
) = 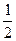 ∙(0,87 + 0,85) = 0,5 ∙1,72 = 0,86
∙(0,87 + 0,85) = 0,5 ∙1,72 = 0,86
2 КВ.
F(-2) = 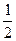 ∙(
∙(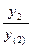 +
+ 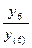 ) =
) = 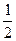 ∙(
∙(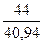 +
+ 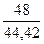 ) =
) = 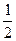 ∙(1,07 + 1,08) = 0,5 ∙ 2,15 = 1,075
∙(1,07 + 1,08) = 0,5 ∙ 2,15 = 1,075
3 КВ.
F(-1) = 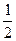 ∙(
∙(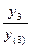 +
+ 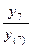 ) =
) = 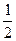 ∙(
∙(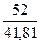 +
+ 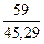 ) =
) = 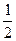 ∙(1,24 + 1,30) = 0,5 ∙ 2,54 = 1,27
∙(1,24 + 1,30) = 0,5 ∙ 2,54 = 1,27
4 КВ.
F(0) = 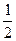 ∙(
∙(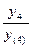 +
+ 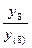 ) =
) = 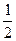 ∙(
∙(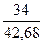 +
+ 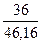 ) =
) = 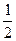 ∙(0,80 + 0,78) = 0,5 ∙ 1,58 = 0,79
∙(0,80 + 0,78) = 0,5 ∙ 1,58 = 0,79
I.
Постройка модели.
|
t
|
yt
|
a(t)
|
b(t)
|
F(t)
|
Y(t)
|
E(t)
|
E2(t)
|
[ E(t+1)-E(t)]2
|
E(t)∙E(t+1)
|
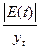 ∙100% ∙100%
|
|
|
|
1
|
35
|
40,26
|
0,929
|
0,866
|
34,46
|
0,54
|
0,292
|
0,672
|
-0,15
|
1,54
|
|
|
2
|
44
|
41,11
|
0,905
|
1,072
|
44,28
|
-0,28
|
0,078
|
1,166
|
0,38
|
0,64
|
|
|
3
|
52
|
41,69
|
0,807
|
1,258
|
53,36
|
-1,36 *
|
1,85
|
3,204
|
-0,58
|
2,61
|
|
|
4
|
34
|
42,66
|
0,851
|
0,8
|
33,57
|
0,43 *
|
0,185
|
1,232
|
-0,29
|
1,26
|
|
|
5
|
37
|
43,28
|
0,782
|
0,856
|
37,68
|
-0,68 *
|
0,462
|
2,102
|
-0,52
|
1,84
|
|
|
6
|
48
|
44,27
|
0,844
|
1,0076
|
47,23
|
0,77
|
0,593
|
2,19
|
1,73
|
1,6
|
|
|
7
|
59
|
45,65
|
1,97
|
1,277
|
56,75
|
2,25 *
|
5,062
|
18,922
|
-4,72
|
3,81
|
|
|
8
|
36
|
46,83
|
1,733
|
0,782
|
38,1
|
-2,1 *
|
4,41
|
2,372
|
1,18
|
5,83
|
|
|
9
|
41
|
48,36
|
1,672
|
0,852
|
41,56
|
-0,56
|
0,314
|
1,613
|
1,02
|
1,36
|
|
|
10
|
52
|
49,52
|
1,518
|
1,06
|
53,83
|
-1,83
|
3,349
|
1,796
|
5,8
|
3,52
|
|
|
11
|
62
|
50,29
|
1,317
|
1,249
|
65,17
|
-3,17 *
|
10,049
|
0,656
|
7,48
|
5,11
|
|
|
12
|
38
|
50,7
|
1,045
|
0,763
|
40,36
|
-2,36
|
5,57
|
18,233
|
-4,51
|
6,21
|
|
|
13
|
46
|
52,42
|
1,247
|
0,869
|
44,09
|
1,91 *
|
3,648
|
7,84
|
-1,7
|
4,15
|
|
|
14
|
56
|
53,42
|
1,173
|
1,054
|
56,89
|
-0,89
|
0,792
|
0,09
|
1,06
|
1,59
|
|
|
15
|
67
|
54,3
|
1,085
|
1,238
|
68,19
|
-1,19
|
1,416
|
0,005
|
1,5
|
1,78
|
|
|
16
|
41
|
54,89
|
0,936
|
0,755
|
42,26
|
-1,26
|
1,588
|
|
|
3,07
|
|
|
|
|
|
|
|
|
|
39,66
|
62,09
|
7,68
|
45,92
|
|
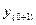 =
=
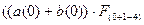
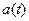 =
= 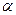 1
∙
1
∙ 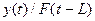 + (1-
+ (1-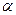 1)
∙
1)
∙ 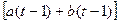
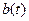 =
=
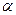 3
∙
3
∙ 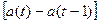 + (
+ (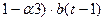
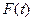 =
= 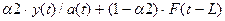
y(1) = (39,20 + 0,87)
∙ 0,86 = 34,46
a(1) = 0,3∙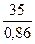 + (1 – 0,3)(39,20 +
0,87) = 12,21 + 0,7 ∙ 40,07 = 40,26
+ (1 – 0,3)(39,20 +
0,87) = 12,21 + 0,7 ∙ 40,07 = 40,26
b(1) =
0,3∙(40,26 – 39,20) + 0,7 ∙ 0,87 = 0,929
F(1) = 0,6∙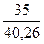 + (1-0,6) ∙ 0,86
= 0,866
+ (1-0,6) ∙ 0,86
= 0,866
y(2) = (40,26 + 0,929)
∙ 1,075 = 44,28
a(2) = 0,3∙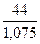 + 0,7∙(40,26 + 0,929) = 41,11
+ 0,7∙(40,26 + 0,929) = 41,11
b(2) =
0,3∙(41,11 – 40,26) + 0,7 ∙ 0,929 = 0,905
F(2) = 0,6∙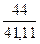 + 0,4 ∙ 1,075 = 1,072
+ 0,4 ∙ 1,075 = 1,072
y(3) = (41,11 +
0,905) ∙ 1,27 = 53,36
a(3) = 0,3∙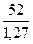 + 0,7∙(41,11 + 0,905) = 41,69
+ 0,7∙(41,11 + 0,905) = 41,69
b(3) =
0,3∙(41,69 – 41,11) + 0,7 ∙ 0,905 = 0,807
F(3) = 0,6∙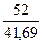 + 0,4 ∙ 1,27 = 1,258
+ 0,4 ∙ 1,27 = 1,258
y(4) = (41,69 +
0,807) ∙ 0,79 = 33,57
a(4) = 0,3∙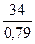 + 0,7∙(41,69 + 0,807) = 42,66
+ 0,7∙(41,69 + 0,807) = 42,66
b(4) =
0,3∙(42,66 – 41,69) + 0,7∙ 0,807 = 0,851
F(4) = 0,6∙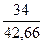 + 0,4 ∙ 0,79 = 0,8
+ 0,4 ∙ 0,79 = 0,8
y(5) = (42,66 +
0,851) ∙ 0,866 = 37,68
a(5) = 0,3∙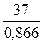 + 0,7∙(42,66 + 0,851) = 43,28
+ 0,7∙(42,66 + 0,851) = 43,28
b(5) =
0,3∙(43,28 – 42,66) + 0,7 ∙ 0,851 = 0,782
F(5) = 0,6∙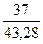 + 0,4 ∙ 0,866 = 0,856
+ 0,4 ∙ 0,866 = 0,856
y(6) = ( 43,28 +
0,782) ∙ 1,072 = 47,23
a(6) = 0,3∙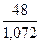 + 0,7∙(43,28 + 0,782) = 44,27
+ 0,7∙(43,28 + 0,782) = 44,27
b(6) =
0,3∙(44,27 – 43,28) + 0,7 ∙ 0,782 = 0,844
F(6) = 0,6∙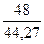 + 0,4 ∙ 1,072 = 1,076
+ 0,4 ∙ 1,072 = 1,076
y(7) = (44,27 +
0,844) ∙ 1,258 = 56,75
a(7) = 0,3∙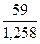 + 0,7∙(44,27 + 0,844) = 45,65
+ 0,7∙(44,27 + 0,844) = 45,65
b(7) =
0,3∙(45,65 – 44,27) + 0,7 ∙ 0,844 = 1,970
F(7) = 0,6∙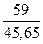 + 0,4 ∙ 1,258 = 1,277
+ 0,4 ∙ 1,258 = 1,277
y(8) = (45,65 +
1,970) ∙ 0,800 = 38,10
a(8) = 0,3∙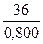 + 0,7∙(45,65 + 1,970) = 46,83
+ 0,7∙(45,65 + 1,970) = 46,83
b(8) =
0,3∙(46,83 – 45,65) + 0,7 ∙ 1,970 = 1,733
F(8) = 0,6∙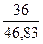 + 0,4 ∙ 0,800 = 0,782
+ 0,4 ∙ 0,800 = 0,782
y(9) = (46,83 +
1,733) ∙ 0,856 = 41,56
a(9) = 0,3∙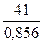 + 0,7∙(46,83 + 1,733) = 48,36
+ 0,7∙(46,83 + 1,733) = 48,36
b(9) =
0,3∙(48,36 – 46,83) + 0,7 ∙ 1,733 = 1,672
F(9) = 0,6∙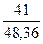 + 0,4 ∙ 0,856 = 0,852
+ 0,4 ∙ 0,856 = 0,852
y(10) = (48,36 +
1,672) ∙ 1,076 = 53,83
a(10) = 0,3∙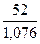 + 0,7 ∙ (48,36 + 1,672) = 49,52
+ 0,7 ∙ (48,36 + 1,672) = 49,52
b(10) =
0,3∙(49,52 – 48,36) + 0,7∙ 1,672 = 1,518
F(10) = 0,6∙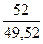 + 0,4 ∙ 1,076 = 1,06
+ 0,4 ∙ 1,076 = 1,06
y(11) = (49,52 + 1,518)
∙ 1,277 = 65,17
a(11) = 0,3∙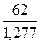 + 0,7∙(49,52 + 1,518) = 50,29
+ 0,7∙(49,52 + 1,518) = 50,29
b(11) =
0,3∙(50,29 – 49,52) + 0,7 ∙ 1,518 = 1,317
F(11) = 0,6∙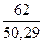 + 04 ∙ 1,277 = 1,249
+ 04 ∙ 1,277 = 1,249
y(12) = (50,29 + 1,317)
∙ 0,782 = 40,36
a(12) = 0,3∙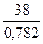 + 0,7∙(50,29 + 1,317) = 50,7
+ 0,7∙(50,29 + 1,317) = 50,7
b(12) =
0,3∙(50,70 – 50,29) + 0,7 ∙ 1,317 = 1,045
F(12) = 0,6∙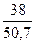 + 0,4 ∙ 0,782 = 0,763
+ 0,4 ∙ 0,782 = 0,763
y(13) = (50,70 +
1,045) ∙ 0,852 = 44,09
a(13) = 0,3∙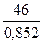 + 0,7∙(50,70 + 1,045) = 52,42
+ 0,7∙(50,70 + 1,045) = 52,42
b(13) =
0,3∙(52,42 50,70) + 0,7 ∙ 1,045 = 1,247
F(13) = 0,6∙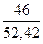 + 0,4 ∙ 0,852 = 0,869
+ 0,4 ∙ 0,852 = 0,869
y(14) = (52,42 +
1,247) ∙ 1,060 = 56,89
a(14) = 0,3∙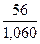 + 0,7∙(52,42 + 1,247) = 53,42
+ 0,7∙(52,42 + 1,247) = 53,42
b(14) =
0,3∙(53,42 – 52,42) + 0,7 ∙ 1,247 = 1,173
F(14) = 0,6∙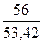 + 0,4 ∙ 1,060 = 1,054
+ 0,4 ∙ 1,060 = 1,054
y(15) = (53,42 + 1,173) ∙ 1,249 = 58,19
a(15) = 0,3∙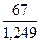 + 0,7 ∙ (53,42 +
1,173) = 54,3
+ 0,7 ∙ (53,42 +
1,173) = 54,3
b(15) = 0,3∙(54,30 – 53,42) + 0,7 ∙ 1,173 =
1,085
F(15) = 0,6∙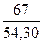 + 0,4 ∙ 1,249 =
1,238
+ 0,4 ∙ 1,249 =
1,238
y(16) = (54,30 + 1,085) ∙ 0,763 = 42,26
a(16) = 0,3∙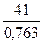 + 0,7∙(54,30 +
1,085) = 54,89
+ 0,7∙(54,30 +
1,085) = 54,89
b(16) = 0,3∙(54,89 – 54,30) + 0,7 ∙ 1,085 =
0,936
F(16) = 0,6∙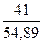 + 0,4 ∙ 0,763 =
0,755
+ 0,4 ∙ 0,763 =
0,755
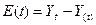
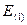 = 35 – 34,46 = 0,54
= 35 – 34,46 = 0,54
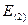 = 44 – 44,28 = -0,28
= 44 – 44,28 = -0,28
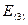 = 52 – 53,36 = -1,36
= 52 – 53,36 = -1,36
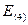 = 34 – 33,57 = 0,43
= 34 – 33,57 = 0,43
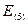 = 37 – 37,68 = -0,68
= 37 – 37,68 = -0,68
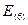 = 48 – 47,23 = 0,77
= 48 – 47,23 = 0,77
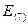 = 59 – 56,75 = 2,25
= 59 – 56,75 = 2,25
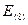 = 36 – 38,10 = -2,1
= 36 – 38,10 = -2,1
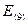 = 41 – 41,56 = -0,56
= 41 – 41,56 = -0,56
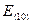 = 52 – 53,83 = -1,83
= 52 – 53,83 = -1,83
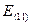 = 62 – 65,17 = -3,17
= 62 – 65,17 = -3,17
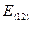 = 38 – 40,36 = -2,36
= 38 – 40,36 = -2,36
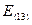 = 46 – 44,09 = 1,91
= 46 – 44,09 = 1,91
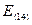 = 56 – 56,89 = -0,89
= 56 – 56,89 = -0,89
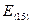 = 67 – 68,19 = -1,19
= 67 – 68,19 = -1,19
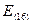 = 41 – 42,26 = -1,26
= 41 – 42,26 = -1,26
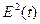

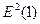 = 0,542 =
0,292
= 0,542 =
0,292
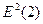 = (-0,28)2
= 0,078
= (-0,28)2
= 0,078
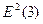 = (-1,36)2
= 1,850
= (-1,36)2
= 1,850
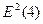 = 0,432 =
0,185
= 0,432 =
0,185
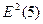 = (-0,68)2
= 0,462
= (-0,68)2
= 0,462
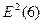 = 0,772 =
0,593
= 0,772 =
0,593
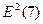 = 2,252 =
5,062
= 2,252 =
5,062
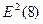 = (-2,1)2 =
4,41
= (-2,1)2 =
4,41
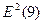 = (-0,56)2
= 0,314
= (-0,56)2
= 0,314
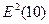 = (-1,83)2
= 3,349
= (-1,83)2
= 3,349
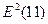 = (-3,17)2
= 10,049
= (-3,17)2
= 10,049
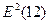 = (-2,36)2
= 5,570
= (-2,36)2
= 5,570
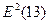 = 1,912 =
3,648
= 1,912 =
3,648
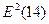 = (-0,89)2
= 0,792
= (-0,89)2
= 0,792
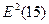 = (-1,19)2
= 1,416
= (-1,19)2
= 1,416
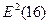 = (-1,26)2
= 1,588
= (-1,26)2
= 1,588
(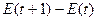 )2
)2
(0,54 + 0,28)2 = 0,672
(-0,28 + 1,36)2 = 1,166
(-1,3 – 0,43)2 = 3,204
(0,43 + 0,68)2 = 1,232
(-0,68 – 0,77)2 = 2,102
(0,77 – 2,25)2 = 2,190
(2,25 +2,1)2 = 18,922
(-2,1 +0,56)2 = 2,372
(-0,56 + 1,83)2 = 1,613
(-1,83 + 3,17)2 = 1,796
(-3,17 + 2,36)2 = 0,656
(-2,36 – 1,91)2 = 18,233
(1,91 + 0,89)2 = 7,84
(-0,89 + 1,19)2 = 0,09
(-1,19 + 1,26)2 = 0,005
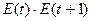
0,54 ∙ (-0,28) = -0,15
(-0,28) ∙ (-1,36) = 0,38
(-1,3) ∙ 0,43 = -0,58
0,43 ∙ (-0,68) = -0,29
(-0,68) ∙ 0,77 = -0,52
0,77 ∙ 2,25 = 1,73
2,25 ∙ (-2,1) = -4,72
(-2,1) ∙ (-0,56) = 1,18
(-0,56) ∙ (-1,83) = 1,02
(-1,83) ∙ (-3,17) = 5,80
(-3,17) ∙ (-2,36) = 7,48
(-2,36) ∙ 1,91 = -4,51
1,91 ∙ (-0,89) = -1,70
(-0,89) ∙ (-1,19) = 1,06
(-1,19) ∙ (-1,26) = 1,50
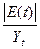 ∙ 100%
∙ 100%
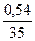 ∙ 100 = 1,54
∙ 100 = 1,54
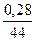 ∙ 100 = 0,64
∙ 100 = 0,64
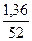 ∙ 100 = 2,61
∙ 100 = 2,61
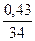 ∙ 100 = 1,26
∙ 100 = 1,26
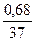 ∙ 100 = 1,84
∙ 100 = 1,84
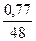 ∙ 100 = 1,60
∙ 100 = 1,60
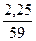 ∙ 100 = 3,81
∙ 100 = 3,81
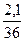 ∙ 100 = 5,83
∙ 100 = 5,83
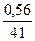 ∙ 100 = 1,36
∙ 100 = 1,36
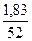 ∙ 100 = 3,52
∙ 100 = 3,52
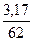 ∙ 100 = 5,11
∙ 100 = 5,11
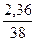 ∙ 100 = 6,21
∙ 100 = 6,21
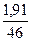 ∙ 100 = 4,15
∙ 100 = 4,15
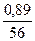 ∙ 100 = 1,59
∙ 100 = 1,59
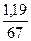 ∙ 100 = 1,78
∙ 100 = 1,78
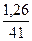 ∙ 100 = 3,07
∙ 100 = 3,07
II.
Оценка точности.
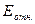 =
= 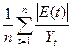 ∙ 100%
∙ 100%
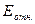 =
= 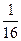 ∙ 45,92 =
∙ 45,92 = 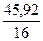 = 2,87%
= 2,87%
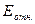 < 5% , условие точности выполнено.
< 5% , условие точности выполнено.
III.
Проверка на
адекватность.
а) проверка на случайность остаточной компоненты.
P = 7 > Pкрит. = 6
Пиковых точек
больше, чем необходимо критических, поэтому
остаточная
компонента является случайной.
б) проверка на независимость уровней
остаточной компоненты.
Критерий – d
Критерий – r1
d = 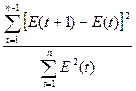
d = 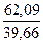 = 1,56
= 1,56
d1 = 1,10 и d2 = 1,37
Если d2 < d < 2, то
уровни ряда остатков являются независимыми.
В нашем случае это условие выполнено,
т.к., 1,37 < 1,56 < 2,
следовательно уровни ряда E(t) независимы.
r1 = 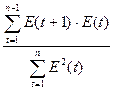
r1 = 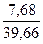 = 0,19
= 0,19
rкр. = 0,32
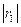 < rкр., следовательно
уровни независимы.
< rкр., следовательно
уровни независимы.
в) соответствие уровней остаточной компоненты
нормальному закону распределения.
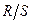 =
= 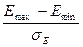 ,
,
где 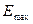 - максимальное значение уровней ряда остатков
- максимальное значение уровней ряда остатков 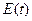 ;
;
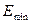 - минимальное значение
уровней ряда остатков
- минимальное значение
уровней ряда остатков 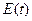 .
.
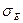 =
= 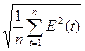
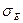 =
= 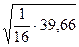 =
= 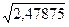 = 1,57
= 1,57
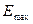 = 2,25
= 2,25
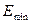 = -3,17
= -3,17
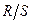 =
= 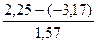 =
= 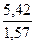 = 3,45
= 3,45
Так как 3 < 3,45 < 4,21, полученное
значение 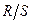 попало в заданный
интервал.
попало в заданный
интервал.
Значит, уровни ряда остатков подчиняются
нормальному
распределению.
Все условия адекватности и точности выполнены. Следовательно,
можно говорить об удовлетворительном
качестве модели и
возможности проведения
прогноза на четыре квартала вперёд.
IV.
Прогноз на год
вперёд.
|
Шаг
прогноза.
|
Время,
t + k
|
Значение
y ∙ (t + k)
|
|
|
|
1
|
17
|
48,51
|
|
|
2
|
18
|
59,83
|
|
|
3
|
19
|
71,43
|
|
|
4
|
20
|
44,27
|
|
y
∙ (t + k) = 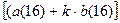 ∙ F(t+k-4)
∙ F(t+k-4)
y(17)
= (54,89 +1 ∙ 0,936) ∙ 0,869 = 55,826 ∙ 0,869 = 48,51
y(18)
= (54,89 +2 ∙ 0,936) ∙ 1,054 = 56,762 ∙ 1,054 = 59,83
y(19)
= (54,89 +3 ∙ 0,936) ∙ 1,238 = 57,698 ∙ 1, 238 = 71,43
y(20)
= (54,89 +4 ∙ 0,936) ∙ 0,755 = 58,634 ∙ 0,755 = 44,27
V.
Построение
графика.
График строим по данным таблицы.
|
Время
|
Факт.
|
Расчёт.
|
|
|
|
1
|
35
|
34,46
|
|
|
2
|
44
|
44,28
|
|
|
3
|
52
|
53,36
|
|
|
4
|
34
|
33,57
|
|
|
5
|
37
|
37,68
|
|
|
6
|
48
|
47,23
|
|
|
7
|
59
|
56,75
|
|
|
8
|
36
|
38,1
|
|
|
9
|
41
|
41,56
|
|
|
10
|
52
|
53,83
|
|
|
11
|
62
|
65,17
|
|
|
12
|
38
|
40,36
|
|
|
13
|
46
|
44,09
|
|
|
14
|
56
|
56,89
|
|
|
15
|
67
|
68,19
|
|
|
16
|
41
|
42,26
|
|
|
17
|
|
48,51
|
|
|
18
|
|
59,83
|
|
|
19
|
|
71,43
|
|
|
20
|
|
44,27
|
|
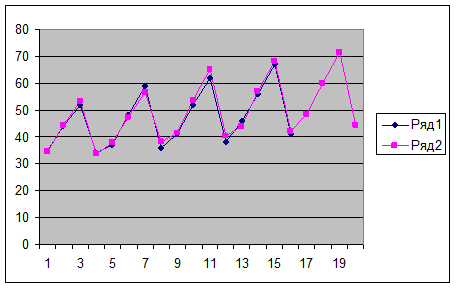
На нижеприведённом рисунке проводится
сопоставление
фактических и расчётных данных. Здесь же
показаны прогнозные
значения цены акции на 1 год вперёд. Из
рисунка видно, что
расчётные данные хорошо согласуются с
фактическими, что говорит
об удовлетворительном качестве прогноза.
Задание 2.
Даны цены (открытия, максимальная,
минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным пяти
дням. Рассчитать:
- экспоненциальную скользящую среднюю;
- момент;
- скорость изменения цен;
- индекс относительной силы;
- %К.
Расчёты проводить для всех дней, для которых
эти расчёты можно выполнить на основании имеющихся данных.
Решение:
Даны
цены (открытия, максимальная, минимальная и закрытия) за 10 дней.
|
Дни, t
|
Цены
|
|
max, Ht
|
min, Lt
|
Закр., Ct
|
|
1
|
718
|
660
|
675
|
|
2
|
685
|
601
|
646
|
|
3
|
629
|
570
|
575
|
|
4
|
585
|
501
|
570
|
|
5
|
598
|
515
|
523
|
|
6
|
535
|
501
|
506
|
|
7
|
555
|
500
|
553
|
|
8
|
580
|
540
|
570
|
|
9
|
580
|
545
|
564
|
|
10
|
603
|
550
|
603
|
1) Найти экспоненциальную скользящую
среднюю.
|
Дни, t
|
Цены
|
EMAt
|
|
max, Ht
|
min, Lt
|
Закр., Ct
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
718
|
660
|
675
|
675
|
|
2
|
685
|
601
|
646
|
665
|
|
3
|
629
|
570
|
575
|
635
|
|
4
|
585
|
501
|
570
|
613
|
|
5
|
598
|
515
|
523
|
583
|
|
6
|
535
|
501
|
506
|
557
|
|
7
|
555
|
500
|
553
|
556
|
|
8
|
580
|
540
|
570
|
561
|
|
9
|
580
|
545
|
564
|
562
|
|
10
|
603
|
550
|
603
|
576
|
n = 5
Находим
коэффициент k по формуле k = 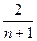
k = 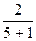 =
= 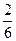 =
= 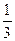
Находим
экспоненциальную скользящую среднюю по формуле
EMAt = k ∙ Ct + (1 – k) ∙ EMAt – 1
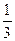 ∙
646 + (1 -
∙
646 + (1 - 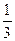 ) ∙ 675 =
) ∙ 675 = 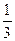 ∙ 646 +
∙ 646 + 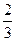 ∙ 675 =
∙ 675 = 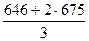 =
= 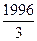 = 665
= 665
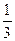 ∙ 575 +
∙ 575 + 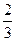 ∙ 665 =
∙ 665 = 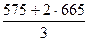 =
= 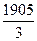 = 635
= 635
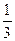 ∙ 570 +
∙ 570 + 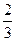 ∙ 635 =
∙ 635 = 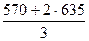 =
= 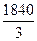 = 613
= 613
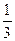 ∙ 523 +
∙ 523 + 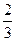 ∙ 613 =
∙ 613 = 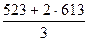 =
= 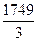 = 583
= 583
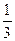 ∙ 506 +
∙ 506 + 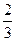 ∙ 583 =
∙ 583 = 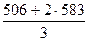 =
=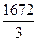 = 557
= 557
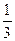 ∙ 553 +
∙ 553 + 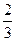 ∙ 557 =
∙ 557 = 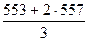 =
= 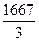 = 556
= 556
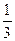 ∙ 570 +
∙ 570 + 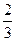 ∙ 556 =
∙ 556 = 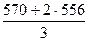 =
= 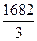 = 561
= 561
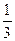 ∙ 564 +
∙ 564 + 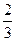 ∙ 561 =
∙ 561 = 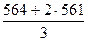 =
= 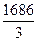 = 562
= 562
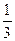 ∙ 603 +
∙ 603 + 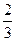 ∙ 562 =
∙ 562 = 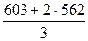 =
= 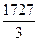 = 576
= 576
Полученные
значения заносим в графу 5.
2) Найти
момент.
|
Дни, t
|
Цены
|
EMAt
|
MOMt
|
|
max, Ht
|
min, Lt
|
Закр., Ct
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
718
|
660
|
675
|
675
|
|
|
2
|
685
|
601
|
646
|
665
|
|
|
3
|
629
|
570
|
575
|
635
|
|
|
4
|
585
|
501
|
570
|
613
|
|
|
5
|
598
|
515
|
523
|
583
|
|
|
6
|
535
|
501
|
506
|
557
|
-169
|
|
7
|
555
|
500
|
553
|
556
|
-93
|
|
8
|
580
|
540
|
570
|
561
|
-5
|
|
9
|
580
|
545
|
564
|
562
|
-6
|
|
10
|
603
|
550
|
603
|
576
|
80
|
Момент
находим по формуле MOMt = Ct – Ct – n
В
графу 6 для t = 6 вносим разность значений из
графы 4: С(6) – С(1), для t =
7
в графу 6 вносим С(7) – С(2) и т.д.
506
– 675 = -169
553 – 646 = -93
570 – 575 = -5
564 – 570 = -6
603 – 523 = 80
3) Найти скорость изменения цен.
|
Дни, t
|
Цены
|
EMAt
|
MOMt
|
ROCt
|
|
max, Ht
|
min, Lt
|
Закр., Ct
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
718
|
660
|
675
|
675
|
|
|
|
2
|
685
|
601
|
646
|
665
|
|
|
|
3
|
629
|
570
|
575
|
635
|
|
|
|
4
|
585
|
501
|
570
|
613
|
|
|
|
5
|
598
|
515
|
523
|
583
|
|
|
|
6
|
535
|
501
|
506
|
557
|
-169
|
75
|
|
7
|
555
|
500
|
553
|
556
|
-93
|
86
|
|
8
|
580
|
540
|
570
|
561
|
-5
|
99
|
|
9
|
580
|
545
|
564
|
562
|
-6
|
99
|
|
10
|
603
|
550
|
603
|
576
|
80
|
115
|
Скорость
изменения цен находим по формуле ROCt = 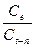 ∙ 100%
∙ 100%
В
графу 7 для t = 6 вносим значения из графы 4: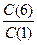 ∙ 100, для t =
∙ 100, для t =
7
в графу 7 вносим 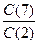 ∙ 100 и т.д.
∙ 100 и т.д.
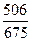 ∙ 100 = 0,749 ∙ 100 = 75
∙ 100 = 0,749 ∙ 100 = 75
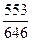 ∙ 100 = 0,856
∙ 100 = 86
∙ 100 = 0,856
∙ 100 = 86
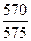 ∙ 100 = 0,991
∙ 100 = 99
∙ 100 = 0,991
∙ 100 = 99
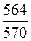 ∙ 100 = 0,989
∙ 100 = 99
∙ 100 = 0,989
∙ 100 = 99
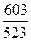 ∙ 100 = 1,152
∙ 100 = 115
∙ 100 = 1,152
∙ 100 = 115
4) Найти индекс относительной силы.
675 646
575 570 523
506 553 570
564 603
-29
-71 -5 -47
-17 +47 +17
-6 +39
|
Дни, t
|
Цена закрытия, Ct
|
Повышение цены
|
Понижение цены
|
AU
|
AD
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
|
1
|
675
|
|
|
|
|
|
|
2
|
646
|
0
|
29
|
|
|
|
|
3
|
575
|
0
|
71
|
|
|
|
|
4
|
570
|
0
|
5
|
|
|
|
|
5
|
523
|
0
|
47
|
|
|
|
|
6
|
506
|
0
|
17
|
0
|
169
|
|
|
7
|
553
|
47
|
0
|
47
|
140
|
|
|
8
|
570
|
17
|
0
|
64
|
69
|
|
|
9
|
564
|
0
|
6
|
64
|
70
|
|
|
10
|
603
|
39
|
0
|
103
|
23
|
|
Индекс
относительной силы находим по формуле RSI = 100 - 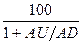 ,
,
- где AU
и AD - сумма приростов и убыли
конечных цен за n дней.
Начиная
со 2 дня до конца таблицы, абс. значение разности между текущей
ценой
и ценой предыдущего дня записываем в графу 3 (если цена возросла)
или
в графу 4 (если цена понизилась).
Начиная
с шестого дня до конца таблицы в графу 5, содержащую сумму
повышений
цен AU, вносим сумму приростов цен из графы 3 за 5 последних
дней.
Эту сумму определяем сложением значений графы 3 за 5 последних
дней.
Для t=6 это будет суммирование значений графы 3 со 2-го дня по 6-ой
включительно,
для t=7 это будут суммироваться значения
графы 3 с 3-го дня
по
7-й и т.д. до конца таблицы.
Аналогично
заполняем графу 6, внося в нее сумму значений из графы 4 за
последние
5 дней.
Рассчитываем RSI = 100 - 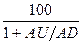 , где AU
и AD берем из 5-й и 6-й графы таблицы.
, где AU
и AD берем из 5-й и 6-й графы таблицы.
100
- 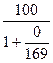 = 100 – 100 = 0
= 100 – 100 = 0
100
- 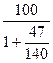 = 100 -
= 100 - 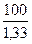 = 100 – 75 = 25
= 100 – 75 = 25
100
- 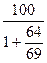 = 100 -
= 100 - 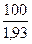 = 100 – 52 = 48
= 100 – 52 = 48
100
- 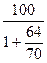 = 100 -
= 100 - 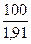 = 100 – 52 = 48
= 100 – 52 = 48
100
- 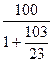 = 100 -
= 100 - 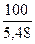 = 100 – 18,24 = 82
= 100 – 18,24 = 82
Полученные
значения заносим в графу 8.
|
Дни, t
|
Цены
|
EMAt
|
MOMt
|
ROCt
|
RSI
|
|
max, Ht
|
min, Lt
|
Закр., Ct
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
718
|
660
|
675
|
675
|
|
|
|
|
2
|
685
|
601
|
646
|
665
|
|
|
|
|
3
|
629
|
570
|
575
|
635
|
|
|
|
|
4
|
585
|
501
|
570
|
613
|
|
|
|
|
5
|
598
|
515
|
523
|
583
|
|
|
|
|
6
|
535
|
501
|
506
|
557
|
-169
|
75
|
0
|
|
7
|
555
|
500
|
553
|
556
|
-93
|
86
|
25
|
|
8
|
580
|
540
|
570
|
561
|
-5
|
99
|
48
|
|
9
|
580
|
545
|
564
|
562
|
-6
|
99
|
48
|
|
10
|
603
|
550
|
603
|
576
|
80
|
115
|
82
|
5) Найти %K.
|
Дни, t
|
Цены
|
EMAt
|
MOMt
|
ROCt
|
RSI
|
%Kt
|
|
max, Ht
|
min, Lt
|
Закр., Ct
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
1
|
718
|
660
|
675
|
675
|
|
|
|
|
|
2
|
685
|
601
|
646
|
665
|
|
|
|
|
|
3
|
629
|
570
|
575
|
635
|
|
|
|
|
|
4
|
585
|
501
|
570
|
613
|
|
|
|
|
|
5
|
598
|
515
|
523
|
583
|
|
|
|
10
|
|
6
|
535
|
501
|
506
|
557
|
-169
|
75
|
0
|
3
|
|
7
|
555
|
500
|
553
|
556
|
-93
|
86
|
25
|
41
|
|
8
|
580
|
540
|
570
|
561
|
-5
|
99
|
48
|
71
|
|
9
|
580
|
545
|
564
|
562
|
-6
|
99
|
48
|
65
|
|
10
|
603
|
550
|
603
|
576
|
80
|
115
|
82
|
100
|
Значение
%К находим по формуле %Кt = 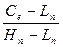 ∙ 100%
∙ 100%
где Ct – цена закрытия на момент t,
Hn, Ln
- максимальная и минимальная цена за 5 предшествующих интервалов.
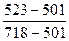 ∙ 100 =
∙ 100 = 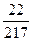 ∙ 100 = 10
∙ 100 = 10
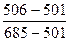 ∙ 100 =
∙ 100 = 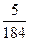 ∙ 100 = 3
∙ 100 = 3
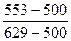 ∙ 100 =
∙ 100 = 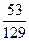 ∙ 100 = 41
∙ 100 = 41
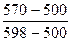 ∙ 100 =
∙ 100 = 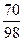 ∙ 100 = 71
∙ 100 = 71
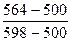 ∙ 100 =
∙ 100 = 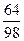 ∙ 100 =65
∙ 100 =65
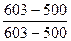 ∙ 100 =
∙ 100 = 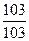 ∙ 100 = 100
∙ 100 = 100
Полученные
значения заносим в графу 9.
Задание 3.
Задача 3.1.
Банк
выдал ссуду, размером 2500000 руб. Дата выдачи ссуды – 15.01.02., возврата –
15.03.02. День выдачи и день возврата считать за 1 день. Проценты
рассчитываются по простой процентной ставке 0.3% годовых.
Найти:
а)
точные проценты с точным числом дней ссуды;
б)
обыкновенные проценты с точным числом дней ссуды;
в)
обыкновенные проценты с приближённым числом дней ссуды.
Решение:
Дано:
S = 2500000 руб. - сумма
Tн = 15.01.02 - начальная дата
Tк =
15.03.02 - конечная
дата
i= 30% = 0,3% - процентная ставка
———————————————
Рассчитываем по формуле S ∙ i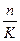
а) K = 365, n = 59
n = 17 + 28 + 14 = 59
2500000
∙ 0,3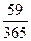 = 2500000 ∙
0,048 = 120000;
= 2500000 ∙
0,048 = 120000;
б) K = 360, n = 59
2500000
∙ 0,3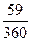 = 2500000 ∙
0,049 = 122500;
= 2500000 ∙
0,049 = 122500;
в) K = 360, n = 57
2500000
∙ 0,3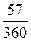 = 2500000 ∙
0,047 = 117500.
= 2500000 ∙
0,047 = 117500.
Ответ:
Точные проценты с точным числом дней ссуды составляют
120000,
обыкновенные проценты с точным числом дней ссуды
составляют 122500,
обыкновенные проценты с приближённым числом дней ссуды
составляют 117500.
Задача 3.2.
Через 180 дней после подписания договора должник
уплатит 2500000 руб. Кредит выдан под 0,3% годовых (проценты обыкновенные).
Какова первоначальная сумма и дисконт?
Решение:
Дано:
S = 2500000 руб.
Тдн = 180
i = 0,3%
Найти:
P, D - ?
———————————————
Рассчитываем
по формулам P = S / (1 + i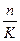 ), D = S – P
), D = S – P
P = 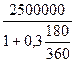 =
= 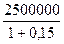 =
= 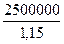 = 2173913 руб.
= 2173913 руб.
D = 2500000 – 2173913 = 326087 руб.
Ответ:
Первоначальная
сумма составляет 2173913 руб., дисконт равен
326087
руб.
Задача 3.3.
Через
180 дней предприятие должно получить по векселю 2500000 руб. Банк приобрёл этот
вексель с дисконтом. Банк учёл вексель по учётной ставке 0,3% годовых (год
равен 360 дням). Определить полученную предприятием сумму и дисконт.
Решение:
Дано:
S = 2500000 руб.
Тдн = 180
i = 0,3%
Найти:
P, D - ?
———————————————
Рассчитываем
по формулам D = S ∙ i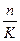 , P = S – D
, P = S – D
D = 2500000 ∙ 0,3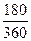 = 2500000 ∙ 0,15
= 375000 руб.
= 2500000 ∙ 0,15
= 375000 руб.
P = 2500000 – 375000 = 2125000 руб.
Ответ:
Полученная
предприятием сумма составляет 2125000 руб., дисконт
равен
375000 руб.
Задача 3.4.
В
кредитном договоре на сумму 2500000 руб. и сроком на 4 года,
зафиксирована
ставка сложных процентов, равная 0,3% годовых. Определить наращенную сумму.
Решение:
Дано:
S = 2500000 руб.
Тлет = 4 года
i = 0,3%
Найти:
Наращенная сумма - ?
———————————————
Рассчитываем
по формуле S ∙ (1 +
i)Тлет
2500000
∙ (1 + 0,3)4 = 2500000
∙ 1,34 = 2500000
∙ 2,8561 = 7140250 руб.
Ответ:
Наращенная
сумма составляет 7140250 руб.
Задача 3.5.
Ссуда,
размером 2500000 руб. предоставлена на 4 года. Проценты сложные, ставка – 0,3%
годовых. Проценты начисляются 2 раза в году. Вычислить наращенную сумму.
Решение:
Дано:
S = 2500000 руб.
Тлет = 4 года
i = 0,3%
m = 2
- число начислений процентов в году
Найти:
Наращенная сумма - ?
———————————————
Рассчитываем
по формуле S ∙ (1 +
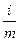 )Tлет
∙m
)Tлет
∙m
2500000
∙ (1 + 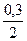 )4 ∙ 2
= 2500000 ∙ 1,58 = 2500000 ∙ 3,059 = 7647500 руб.
)4 ∙ 2
= 2500000 ∙ 1,58 = 2500000 ∙ 3,059 = 7647500 руб.
Ответ:
Наращенная
сумма составляет 7647500 руб.
Задача 3.6.
Вычислить
эффективную ставку процента, если банк начисляет проценты 2 раза в году, исходя
из номинальной ставки 0,3% годовых.
Решение:
Дано:
m = 2
i = 0,3%
Найти:
iэф - ?
———————————————
Рассчитываем
по формуле iэф = (1 + 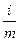 )m – 1
)m – 1
iэф = (1 + 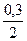 )2 – 1 = 1,152 – 1 = 1,3225 – 1 =
0,3225 = 32,25%
)2 – 1 = 1,152 – 1 = 1,3225 – 1 =
0,3225 = 32,25%
Ответ:
Эффективная
ставка процента составляет 32,25%.
Задача 3.7.
Определить,
какой должна быть номинальная ставка при начислении процентов 2 раза в году,
чтобы обеспечить эффективную ставку 0,3% годовых.
Решение:
Дано:
m = 2
i = 0,3%
Найти:
iном - ?
———————————————
Рассчитываем
по формуле iном = [(1 + iэф) 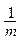 - 1] ∙ m
- 1] ∙ m
iном = [(1 + 0,3)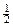 - 1] ∙ 2 =
(
- 1] ∙ 2 =
(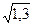 - 1) ∙2 =
(1,14017 – 1) ∙ 2 = 0,14017 ∙2 =
- 1) ∙2 =
(1,14017 – 1) ∙ 2 = 0,14017 ∙2 =
=
0,28034 = 28,03%
Ответ:
Номинальная
ставка составляет 28,03%
Задача 3.8.
Через
4 года предприятию будет выплачена сумма 2500000. Определить её современную
стоимость при условии, что применяется сложная процентная ставка 0,3% годовых.
Решение:
Дано:
S = 2500000 руб.
Тлет = 4 года
i = 0,3%
Найти:
P - ?
———————————————
Рассчитываем
по формуле P = 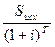
P = 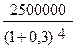 =
= 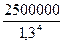 =
= 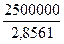 = 875319,49 руб.
= 875319,49 руб.
Ответ:
Современная
стоимость составляет 875319,49 руб.
Задача 3.9.
Через
4 года по векселю должна быть выплачена сумма 2500000 руб. Банк учёл вексель по
сложной учётной ставке 0,3% годовых. Определить дисконт.
Решение:
Дано:
S = 2500000 руб.
Тлет = 4 года
i = 0,3%
Найти:
D - ?
———————————————
Рассчитываем
по формулам P = Sисх ∙ (1 – i)Тлет,
D = S – P
P = 2500000 ∙ (1 – 0,3)4 = 2500000
∙ 0,74 = 0,2401 ∙ 2500000 = 600250 руб.
D = 2500000 – 600250 = 1899750 руб.
Ответ:
Дисконт
составляет 1899750 руб.
Задача 3.10.
В
течение 4 лет на расчётный счёт в конце каждого года поступает по 2500000 руб.,
на которые 2 раза в году начисляются проценты по сложной годовой ставке 0,3% .
Определить сумму на расчётном счёте к концу указанного срока.
Решение:
Дано:
S = 2500000 руб.
Тлет = 4 года
i = 0,3%
m = 2
Найти:
Сумма на расчётном счёте - ?
———————————————
Рассчитываем
по формуле
((S ∙
(1 + 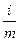 )m + S) ∙ (1 +
)m + S) ∙ (1 + 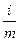 )m + S) ∙ (1 +
)m + S) ∙ (1 + 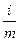 )m + S) ∙ (1 +
)m + S) ∙ (1 + 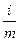 )m
)m
(2500000
∙ 1,152 + 2500000) ∙ 1,152 + 2500000) ∙
1,152 + 2500000) ∙ 1,152
=
(2500000 ∙ 1,3225 + 2500000) ∙ 1,3225 + 2500000) ∙ 1,3225 +
2500000)
∙
1,3225 = (5806250 ∙ 1,3225 + 2500000) ∙ 1,3225 + 2500000) ∙
1,3225 =
=
15961416 ∙ 1,3225 = 21108972 руб.
Ответ:
Сумма
на расчётном счёте составляет 21108972 руб.