МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОУ ВПО
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ
ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Филиал г. Ярославля
КОНТРОЛЬНАЯ РАБОТА
по
дисциплине «Эконометрика»
Выполнила: студентка III курса
специальности
БУА и А
учетно-статистического
факультета
Проверил:
Ярославль
2007
ВАРИАНТ № 11
I ЗАДАНИЕ.
Исходные данные.
|
t
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Y
|
10
|
15
|
21
|
23
|
25
|
34
|
32
|
37
|
41
|
На основании данных,
приведенных в табл. 1. Требуется:
1) определить наличие тренда Y(t);
2) построить линейную модель Y(t)
= ao + a1t, параметры которой оценить МНК;
3) оценить адекватность построенной модели на основе исследования:
-
случайности остаточной компоненты по критерию пиков;
-
независимости уровней ряда остатков по d-критерию (в качестве критических значений следует использовать уровни d1 = 1,08 и d2 = 1,36) и по первому
коэффициенту автокорреляции, критический
уровень которого r(1) = 0,36;
-
нормальности распределения остаточной компоненты по R/S-критерию с критическими уровнями 2,7
– 3,7;
3) для оценки точности модели используйте среднеквадратическое
отклонение и среднюю по модулю относительную ошибку;
4) построить точечный и
интервальный прогнозы на два шага вперед (для вероятности
Р= 70% используйте коэффициент = 1,11);
5) отобразить на графике фактические данные, результаты расчетов и
прогнозирования.
РЕШЕНИЕ
Ввод
исходных данных
Исходные
данные к задаче 1
|
t
|
y
|
|
1
|
10
|
|
2
|
15
|
|
3
|
21
|
|
4
|
23
|
|
5
|
25
|
|
6
|
34
|
|
7
|
32
|
Решение:
1. Тренд – это
основная существующая тенденция.
Аномальных явлений нет.
Весь ряд делим на группы: 1
группа – 4 значения
2
группа – 5 значений
Тренд есть если
среднее 1 группы существенно отличается от среднего 2 группы.
С помощью статистических гипотез
проверим являются ли эти две величины разными.
Проверяем гипотезу об
однородности дисперсий.
Для каждой
группы определим дисперсию и среднее по формулам:
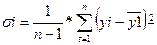
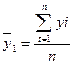
Таблица 1.
|
Двухвыборочный
F-тест для дисперсии
|
|
|
|
|
|
|
|
Переменная 1
|
Переменная 2
|
|
Среднее
|
17,25
|
33,8
|
|
Дисперсия
|
34,91666667
|
35,7
|
|
Наблюдения
|
4
|
5
|
|
df
|
3
|
4
|
|
F
|
0,97805789
|
1,022434368
|
|
P(F<=f)
одностороннее
|
0,513429271
|
1,94768794
|
|
F
критическое одностороннее
|
0,109682929
|
9,117189023
|
Используем F- критерий Фишера.
Fрасч. = = 1,022434368.
Fтабл = = 9,117189023.
Fрасч. < Fтабл., следовательно,
гипотеза подтверждается и дисперсии однородны.
Проверяем
гипотезу о примерном равенстве средних.
tрасч. =
-
Таблица 2.
|
Двухвыборочный
t-тест с одинаковыми дисперсиями
|
|
|
|
|
|
|
Переменная 1
|
Переменная 2
|
|
Среднее
|
17,25
|
33,8
|
|
Дисперсия
|
34,91666667
|
35,7
|
|
Наблюдения
|
4
|
5
|
|
Объединенная
дисперсия
|
35,36428571
|
|
|
Гипотетическая
разность средних
|
0
|
|
|
df
|
7
|
|
|
t-статистика
|
-4,148673869
|
|
|
P(T<=t)
одностороннее
|
0,002151112
|
|
|
t
критическое одностороннее
|
1,894577508
|
|
|
P(T<=t)
двухстороннее
|
0,004302223
|
|
|
t
критическое двухстороннее
|
2,36462256
|
|
Используем
критерий Стьюдента.
tрасч. = 2,36462256
tтабл. = 1,894577508
tрасч. > tтабл., следовательно,
гипотеза отклоняется, средние существенно отличаются друг от друга, тренд
существует.
2. Построение линейной модели Y(t)
= ao + a1t,
Построим линейную
однопараметрическую модель регрессии Y от t.
Значение
параметров ao и a1 линейной модели определяется
по формулам:
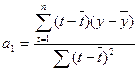
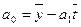
Значение
параметров ao и a1 линейной модели
определим, используя данные таблицы 3. Во
втором столбце табл.3.1 содержатся
коэффициенты уравнения регрессии a0, a1, в третьем столбце – стандартные ошибки коэффициентов уравнения
регрессии, а в четвертом – t-статистика,
используемая для проверки
значимости коэффициентов уравнения регрессии.
Уравнение регрессии
зависимости Yt, от tt (время) имеет вид:
Y(t) =7,86+3,72t
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
|
|
Множественный
R
|
0,983866085
|
|
|
|
|
|
|
|
|
R-квадрат
|
0,967992473
|
|
|
|
|
|
|
|
|
Нормированный
R-квадрат
|
0,96341997
|
|
|
|
|
|
|
|
|
Стандартная
ошибка
|
1,978655949
|
|
|
|
|
|
|
|
|
Наблюдения
|
9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
|
|
|
Регрессия
|
1
|
828,8166667
|
828,8167
|
211,6986
|
1,729E-06
|
|
|
|
|
Остаток
|
7
|
27,40555556
|
3,915079
|
|
|
|
|
|
|
Итого
|
8
|
856,2222222
|
|
|
|
|
|
|
|
Таблица 3.1
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная
ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
|
Y-пересечение
|
7,861111111
|
1,437460221
|
5,46875
|
0,000937
|
4,462060243
|
11,26016
|
4,46206
|
11,26016
|
|
t
|
3,716666667
|
0,255443385
|
14,54986
|
1,73E-06
|
3,112639477
|
4,320694
|
3,112639
|
4,320694
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД
ОСТАТКА
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное y
|
Остатки
|
|
|
|
|
|
|
|
1
|
11,57777778
|
-1,577777778
|
|
|
|
|
|
|
|
2
|
15,29444444
|
-0,294444444
|
|
|
|
|
|
|
|
3
|
19,01111111
|
1,988888889
|
|
|
|
|
|
|
|
4
|
22,72777778
|
0,272222222
|
|
|
|
|
|
|
|
5
|
26,44444444
|
-1,444444444
|
|
|
|
|
|
|
|
6
|
30,16111111
|
3,838888889
|
|
|
|
|
|
|
|
7
|
33,87777778
|
-1,877777778
|
|
|
|
|
|
|
|
8
|
37,59444444
|
-0,594444444
|
|
|
|
|
|
|
|
9
|
41,31111111
|
-0,311111111
|
|
|
|
|
|
|
3. Оценка адекватности
построенной модели. Модель
является адекватной, если для остатков характерны: случайный характер значений,
равенство нулю математического ожидания, отсутствие автокорреляции, нормальный закон
распределения и неизменность дисперсии остатков во времени.
3.1.Проверку
случайности уровней ряда остатков проведем на основе критерия поворотных точек на
основе формулы:
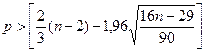
где p – фактическое количество поворотных точек в случайном ряду,
n – число членов исходного ряда наблюдения.
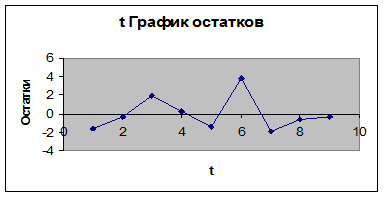
Рисунок 1.
|
p-фактич
|
4
|
|
pкритич.
|
2,451105539
|
Количество
поворотных точек равно 4 (рис. 1). Неравенство выполняется (4>2). Следовательно,
свойство случайности выполняется. Модель по этому критерию адекватна.
3.2.При
проверке независимости (отсутствие
автокорреляции) определяется отсутствие в ряду остатков систематической
составляющей, например, с помощью d-критерия
Дарбина–Уотсона по формуле):
|
Наблю-
дение
|
Предсказанное y
|
Остатки
|
et-e(t-1)
|
(et-e(t-1))2
|
et2
|
et*e(t-1)
|
|
1
|
11,57777778
|
-1,577777778
|
|
|
2,489383
|
|
|
2
|
15,29444444
|
-0,294444444
|
1,283333
|
1,646944
|
0,086698
|
0,464568
|
|
3
|
19,01111111
|
1,988888889
|
2,283333
|
5,213611
|
3,955679
|
-0,58562
|
|
4
|
22,72777778
|
0,272222222
|
-1,71667
|
2,946944
|
0,074105
|
0,54142
|
|
5
|
26,44444444
|
-1,444444444
|
-1,71667
|
2,946944
|
2,08642
|
-0,39321
|
|
6
|
30,16111111
|
3,838888889
|
5,283333
|
27,91361
|
14,73707
|
-5,54506
|
|
7
|
33,87777778
|
-1,877777778
|
-5,71667
|
32,68028
|
3,526049
|
-7,20858
|
|
8
|
37,59444444
|
-0,594444444
|
1,283333
|
1,646944
|
0,353364
|
1,116235
|
|
9
|
41,31111111
|
-0,311111111
|
0,283333
|
0,080278
|
0,09679
|
0,184938
|
|
|
|
|
|
75,07556
|
27,40556
|
-11,4253
|
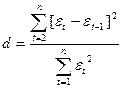
Построим вспомогательную таблицу
для вычисления d-критерия.
Таблица 4.
d = 75,07556/ 27,40556=2,73942834
dn = 4 - 2,73942834 = 1,26057166
Рисунок 2.

dn попало в
интервал от d2 до 2 (рис. 2.), значит модель уровня ряда остатков независима, автокорреляции
нет, свойство независимости выполняется. Модель по этому критерию адекватна.
3.3 Соответствие ряда остатков нормальному закону распределения
определим при помощи RS-критерия:
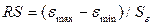
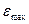 – максимальный
уровень ряда остатков,
– максимальный
уровень ряда остатков, 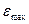 = 3,838888889;
= 3,838888889;
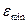 – минимальный уровень ряда остатков,
– минимальный уровень ряда остатков,
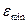 = -1,877777778;
= -1,877777778;
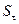 – среднеквадратичное
отклонение,
– среднеквадратичное
отклонение,
Таблица 5.
|
Наблюдение
|
Предсказанное y
|
Остатки Е(t)
|
et-e(t-1)
|
(et-e(t-1))2
|
et2
|
|
1
|
11,57777778
|
-1,577777778
|
|
|
2,489383
|
|
2
|
15,29444444
|
-0,294444444
|
1,283333
|
1,646944
|
0,086698
|
|
3
|
19,01111111
|
1,988888889
|
2,283333
|
5,213611
|
3,955679
|
|
4
|
22,72777778
|
0,272222222
|
-1,71667
|
2,946944
|
0,074105
|
|
5
|
26,44444444
|
-1,444444444
|
-1,71667
|
2,946944
|
2,08642
|
|
6
|
30,16111111
|
3,838888889
|
5,283333
|
27,91361
|
14,73707
|
|
7
|
33,87777778
|
-1,877777778
|
-5,71667
|
32,68028
|
3,526049
|
|
8
|
37,59444444
|
-0,594444444
|
1,283333
|
1,646944
|
0,353364
|
|
9
|
41,31111111
|
-0,311111111
|
0,283333
|
0,080278
|
0,09679
|
|
|
|
|
|
75,07556
|
27,40556
|
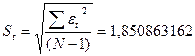
RS=[3,8389–(-1,8778)] /1,8509=3,088649007
Расчетное
значение попадает в интервал (2,7–3,7), следовательно, выполняется свойство
нормальности распределения. Модель по этому критерию адекватна.
Вывод: Все четыре пункта проверки 1-4 дают положительный
результат. Делаем вывод о том, что выбранная трендовая модель является
адекватной реальному ряду экономической динамики.
4. В качестве статистических показателей точности применяют
стандартную ошибку оценки прогнозируемого показателя, или среднеквадратическое
отклонение от линии тренда
где m – число параметров модели, и среднюю относительную
ошибку аппроксимации
S = 1,978655949
Eотн. = 5,966368032
Ошибка равна примерно 6%, что
менее 15%, следовательно, точность модели считается приемлемой и можно делать
прогнозирование.
5. Строим точечный и
интервальный прогнозы на два шага вперед.
Y10= a0 + a1t
=7,86+3,72t = 7,86+3,72 x 10 =
45,02777778;
Y11= a0 + a1t
=7,86+3,72t = 7,86+3,72 x 11 =
48,74444444.
Для
построения интервального прогноза рассчитаем интервал. Будущие значения Yn+k с вероятностью 70% (по условию) и коэффициентом
t равном
1,11 попадут в интервал:
Построим вспомогательную таблицу.
Таблица 6.
|
t-tср
|
(t-tср)2
|
|
-4
|
16
|
|
-3
|
9
|
|
-2
|
4
|
|
-1
|
1
|
|
0
|
0
|
|
1
|
1
|
|
2
|
4
|
|
3
|
9
|
|
4
|
16
|
|
сумма
|
60
|
tср=5 Получим:
Таблица 7.
|
время
|
шаг
|
прогноз
|
дельта
|
ниж.граница
|
верх. гран
|
|
10
|
1
|
45,02777778
|
2,539378188
|
42,4884
|
47,56716
|
|
11
|
2
|
48,74444444
|
2,687425268
|
46,05702
|
51,43187
|
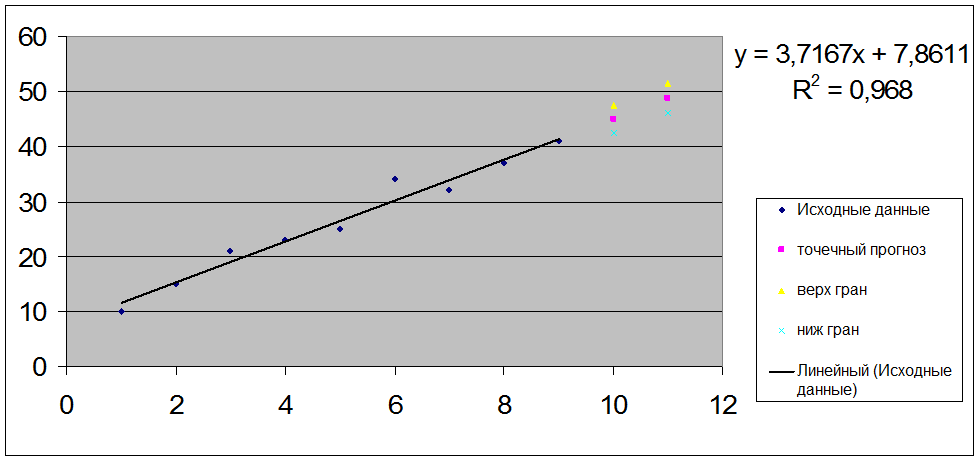
Отобразим на графике фактические данные, результаты расчетов и
прогнозирования.
II
ЗАДАНИЕ.
1 –
построить матрицу коэффициентов парной
корреляции Y(t) с X1(t) и X2(t) и выбрать фактор,
наиболее тесно связанный с зависимой переменной Y(t);
2 – построить линейную однопараметрическую модель регрессии
Y(t) = ao +
a1 X(t);
3 – оценить качество построенной
модели, исследовав ее адекватность и точность;
4 – для модели регрессии рассчитать коэффициент эластичности и бета-коэффициент;
5 - построить точечный и интервальный прогнозы на два шага
вперед по модели регрессии (для вероятности Р
= 70% используйте коэффициент 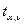 = 1,11) (прогнозные оценки фактора X(t) на два шага вперед получить на основе среднего прироста
от фактически достигнутого уровня).
= 1,11) (прогнозные оценки фактора X(t) на два шага вперед получить на основе среднего прироста
от фактически достигнутого уровня).
Исходные данные.
|
|
ФАКТОРЫ
|
|
Y
|
X1
|
X2
|
|
10
|
16
|
12
|
|
15
|
20
|
17
|
|
21
|
22
|
20
|
|
23
|
20
|
21
|
|
25
|
25
|
25
|
|
34
|
23
|
27
|
|
32
|
25
|
24
|
|
37
|
28
|
28
|
|
41
|
30
|
31
|
1. Построение
системы показателей (факторов). Анализ матрицы коэффициентов парной корреляции.
Выбор наиболее существенного фактора Хt..
Для того чтобы
выбрать фактор наиболее тесно связанный с зависимой переменной, оценим величину
влияния факторов при помощи коэффициента корреляции.
Коэффициент корреляции определяется по формуле:
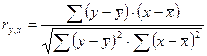
Проведем корреляционный
анализ с помощью EXCEL.
Таблица 8.
|
|
y
|
Х1
|
Х2
|
|
y
|
1
|
|
|
|
Х1
|
0,916909378
|
1
|
|
|
Х2
|
0,970654555
|
0,936283628
|
1
|
Анализ матрицы коэффициентов
парной корреляции показывает, что зависимая переменная Yt
имеет более тесную связь с x2t.
2. Построим линейную
однопараметрическую модель регрессии Y от X2. Регрессионный анализ выполним с помощью надстройки EXCEL Анализ данных.
Результат регрессионного анализа содержится в нижеприведенных
таблицах.
|
ВЫВОД
ИТОГОВ
|
|
|
|
|
|
|
|
|
Регрессионная
статистика
|
|
|
|
|
|
|
|
|
Множественный
R
|
0,970654555
|
|
|
|
|
|
|
|
|
R-квадрат
|
0,942170266
|
|
|
|
|
|
|
|
|
Нормированный
R-квадрат
|
0,933908875
|
|
|
|
|
|
|
|
|
Стандартная
ошибка
|
2,659621438
|
|
|
|
|
|
|
|
|
Наблюдения
|
9
|
|
|
|
|
|
|
|
|
Дисперсионный
анализ
|
|
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
|
|
|
Регрессия
|
1
|
806,7071189
|
806,7071189
|
114,0449974
|
1,38508E-05
|
|
|
|
|
Остаток
|
7
|
49,51510334
|
7,073586191
|
|
|
|
|
|
|
Итого
|
8
|
856,2222222
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
|
Y-пересечение
|
-12,24880763
|
3,730123692
|
-3,283753742
|
0,013417474
|
-21,06914227
|
-3,428472997
|
-21,06914227
|
-3,428472997
|
|
Х2
|
1,69872814
|
0,159069077
|
10,67918524
|
1,38508E-05
|
1,322589812
|
2,074866468
|
1,322589812
|
2,074866468
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД
ОСТАТКА
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное y
|
Остатки
|
E
|
|
|
|
|
|
|
1
|
8,135930048
|
1,864069952
|
0,186406995
|
|
|
|
|
|
|
2
|
16,62957075
|
-1,629570747
|
0,10863805
|
|
|
|
|
|
|
3
|
21,72575517
|
-0,725755167
|
0,03455977
|
|
|
|
|
|
|
4
|
23,42448331
|
-0,424483307
|
0,018455796
|
|
|
|
|
|
|
5
|
30,21939587
|
-5,219395866
|
0,208775835
|
|
|
|
|
|
|
6
|
33,61685215
|
0,383147854
|
0,011269055
|
|
|
|
|
|
|
7
|
28,52066773
|
3,479332273
|
0,108729134
|
|
|
|
|
|
|
8
|
35,31558029
|
1,684419714
|
0,045524857
|
|
|
|
|
|
|
9
|
40,41176471
|
0,588235294
|
0,014347202
|
|
|
|
|
|
|
|
|
|
0,736706693
|
|
|
|
|
|
Во втором столбце табл. 9 содержатся коэффициенты уравнения регрессии a0, a1, в третьем
столбце – стандартные ошибки коэффициентов уравнения регрессии, а в четвертом – t-статистика, используемая для проверки значимости коэффициентов
уравнения регрессии.
Коэффициенты уравнения регрессии a0, a1 вычисляются по
формуле:
|
а0
|
-12,24880763
|
|
а1
|
1,69872814
|
Уравнение регрессии
зависимости Yt, от tt имеет вид:
Y(X) = -12,24880763+1,69872814Xt
3. Для оценки качества регрессионных моделей
целесообразно использовать коэффициент множественной корреляции R, а также характеристики существенности модели в
целом и отдельных её коэффициентов.
Коэффициент
детерминации R2
вычисляется по формуле:
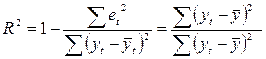
Коэффициент
множественной корреляции R по
формуле:
Эти характеристики приведены в таблице 10 протокола ЕХСЕL.
|
Регрессионная статистика
|
|
Множественный R
|
0,970654555
|
|
R-квадрат
|
0,942170266
|
|
Нормированный
R-квадрат
|
0,933908875
|
|
Стандартная
ошибка
|
2,659621438
|
|
Наблюдения
|
9
|
Таблица 10.
Чем ближе R2 к 1, тем лучше
качество модели.
Для проверки значимости модели регрессии используется F-критерий Фишера. Если расчетное значение больше
табличного, то модель считается значимой.
Fтабл = 5,59145974
Fрасч = 114,0449974
Fтабл < Fрасч
Модель адекватна.
В качестве меры точности
применяют стандартную ошибку оценки:
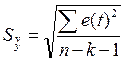 = 2,659621438.
= 2,659621438.
4. Определим коэффициент эластичности и β-коэффициент.
Коэффициент
эластичности показывает, на сколько процентов изменится Y если X2 изменится на 1%.
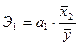 %
%
X2ср= 22,77777778;
Yср= 26,44444444
а1= 1,69872814
Э1= 1,463190205
Таким образом,
при изменении X2 на 1% Y изменится на 1,4632%
β-коэффициент
показывает, на какую долю в среднем изменится среднеквадратическое отклонение
зависимой переменной Y
при изменении X2 на
одно свое среднеквадратическое отклонение при фиксированных значениях остальных
объясняющих переменных.
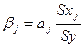
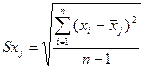
Станд отклонение Х2 = 5,911382617
Станд отклонение Y = 10,34542304
β1=
0,970654555
5. Определим точечный и интервальный прогнозы на два шага
вперед.
Для вычисления прогнозных оценок Y на основе
построенной модели необходимо получить прогнозные оценки фактора Х.
Получим прогнозные оценки фактора на основе величины его среднего абсолютного
прироста САП.
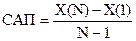 ;
;
CАП = (31-12)/(9-1) = 2,375
Xp(N+l) = X(N) + l ∙ САП;
l=1
Xp(10) = Х(9)+ 2,375 ∙ 1 = 31 -2,375
∙ 1 =33,375;
l=2
Xp(11) = Х(9))+ 2,375∙
2 = 31 -2,375 ∙ 2 =35,75;
Для получения
прогнозных оценок зависимой переменной подставим в модель Y(X) = -12,24880763+1,69872814*Xt найденные
прогнозные значения фактора Х:
Y10 = =-12,24880763+1,69872814* X10-12,24880763+1,69872814*33,375=44,44624404
Y11 = =-12,24880763+1,69872814* X11-12,24880763+1,69872814*35,75=48,48072337
Определим
доверительный интервал прогноза, который будет иметь следующие границы:
-
Верхняя граница прогноза: Yp(N+l) + U(l);
-
Нижняя граница прогноза: Yp(N+l) - U(l).
Величина U(l) имеет вид:
и(l) = S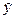 ta
ta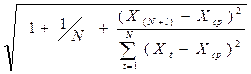 , где
, где
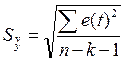 - стандартная ошибка - эта
характеристика приведена в таблице
протокола ЕХСЕL и равна 2,659621438.
- стандартная ошибка - эта
характеристика приведена в таблице
протокола ЕХСЕL и равна 2,659621438.
ta -является табличным значением критерия
Стьюдента для уровня значимости a и для числа степеней свободы, равного N-2. В нашем примере t0,7 = 1,11;
Таблица 11.
|
Наблюдение
|
Х2
|
X-Xср
|
(X-Xср)^2
|
|
1
|
12
|
-10,77777778
|
116,1604938
|
|
2
|
17
|
-5,777777778
|
33,38271605
|
|
3
|
20
|
-2,777777778
|
7,716049383
|
|
4
|
21
|
-1,777777778
|
3,160493827
|
|
5
|
25
|
2,222222222
|
4,938271605
|
|
6
|
27
|
4,222222222
|
17,82716049
|
|
7
|
24
|
1,222222222
|
1,49382716
|
|
8
|
28
|
5,222222222
|
27,27160494
|
|
9
|
31
|
8,222222222
|
67,60493827
|
|
Сумма
|
205
|
|
279,5555556
|
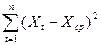 = 279,5555556
= 279,5555556
Хср=205\9=22,77777778
Для прогноза на два шага
имеем:
U(1)
= 3,631090152
U(2) = 3,863930171
Результаты прогнозных оценок по модели регрессии
представим в таблице:
Таблица 12.
|
Время t
|
Шаг k
|
Прогноз Yp(t)
|
Дельта
|
Нижняя граница
|
Верхняя граница
|
|
10
|
1
|
45,02777778
|
2,539378188
|
42,4884
|
47,56716
|
|
11
|
2
|
48,74444444
|
2,687425268
|
46,05702
|
51,43187
|
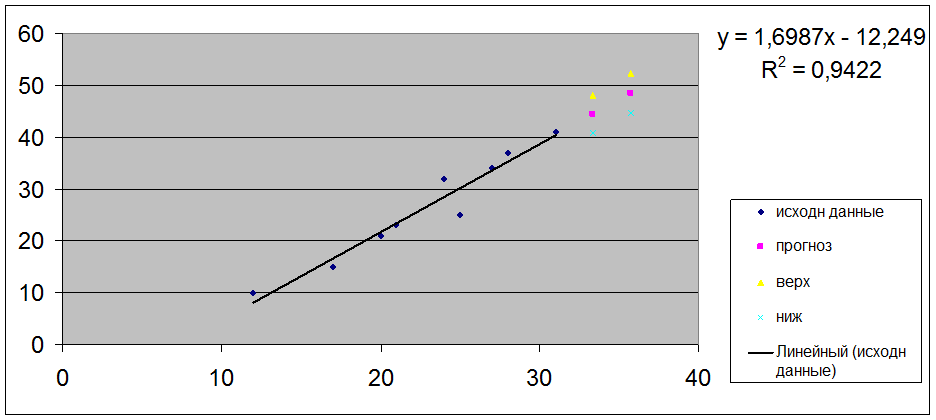
Отобразить на графике фактические данные, результаты расчетов и
прогнозирования.
По условию d2 = 1,36
d1 < d < d2 -
область неопределенности, когда нет оснований ни принять, ни отвергнуть гипотезу
о существовании автокорреляции. Применим другой критерий, в частности первый
коэффициент автокорреляции:
r1 = -0,4169
r1 = 0,41
rтабл = 0,36
rфакт > rтабл