Лабораторная работа № 1. ОСНОВНЫЕ
ПОНЯТИЯ СТАТИСТИКИ И СВОЙСТВА СТАТИСТИЧЕСКОГО РАСПРЕДЕЛЕНИЯ
Цель работы: приобретение навыков
группирования и обработки первичной статистической информации в интерактивной
среде Excel.
Задание. Проранжировать первичный ряд данных, определить частоты и
частости нового ряда, найти абсолютную и относительные плотности распределения,
перегруппировать данные для сопоставления и анализа двух рядов, графически
изобразить кривые (плотности) распределения рядов, представить данные в виде полигона
частот, гистограмм, кумулятивных кривых по известным накопленным частотам.
Условие. Имеются разрозненные данные по рентабельности
активов банков с доходами от 50 до 100 млн. долл.:
1,51; 0,85; 1,37; 1,62; 0,80;
2,0; 1,49; 1,58; 1,75; 1,24; 1,28; 1,04; 1,98; 1,15; 1,66; 1,33; 1,73; 1,13;
1,36; 1,28.
Сравнить полученный
сгруппированный ряд с известным интервальным рядом распределения по уровню
рентабельности активов банков с доходами от 100 до 300 млн. долл.
Табл. 1.
|
Группы
банков с доходами от 100 до 300 млн. долл.
|
|
Рентабельность
активов
|
Количество
банков в % (частости)
|
|
0,6 –
0,8
|
10
|
|
0,8 –
1,0
|
30
|
|
1,0 –
1,1
|
10
|
|
1,1 –
1,2
|
15
|
|
1,2 –
1,4
|
20
|
|
1,4 –
1,8
|
10
|
|
1,8 –
2,0
|
5
|
|
ИТОГО:
|
100
|
Выполнение задания.
1. В программной среде Excel заполняется столбец исходных данных рис. 1.
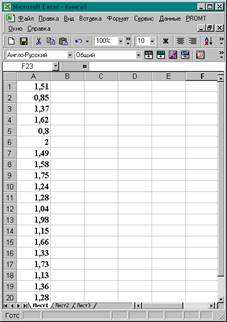
Рис. 1.
2. Выполняется сортировка столбца А - первичного ряда в порядке возрастания. В результате
получен новый интервальный ранжированный ряд рис.2.
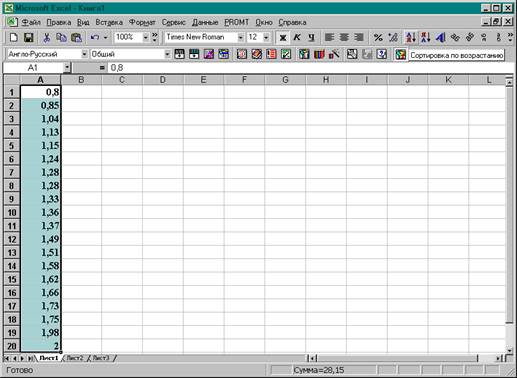
Рис. 2.
3. Определяются частоты и частости
нового ряда. Для этого используется данные об объеме совокупности исследуемых банков N = 20 . Дискретный вариационный ряд разбивается на
интервалы, число которых подсчитывается по формуле Стержесса
k = 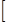 1 +
3,322 lg N
1 +
3,322 lg N 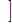 ,
(1)
,
(1)
в которой квадратные скобки
означают округление числа 5,32 , тогда k = 5. Длина частичного интервала определяется по формуле
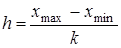 .
(2)
.
(2)
xmax = 2,0 , xmin = 0,8 , h = 0,24. Тогда границы интервалов будут такими:
|
x0=
|
xmin =0,8 ;
|
|
x1=
|
xmin + h = 1,04 ;
|
|
x2=
|
xmin + 2h =
1,28 ;
|
|
x3=
|
xmin + 3h =
1,52 ;
|
|
x4=
|
xmin + 4h =
1,76 ;
|
|
x5=
|
xmin + 5h = 2
.
|
Подсчитывается количество
банков принадлежащих каждому из интервалов. Вычисляется накопленная частота и
процентное отношение частоты к общему объему всей совокупности N = 20 или частость. Для сопоставления полученных данных
интервального вариационного ряда с данными другого вариационного ряда с
неравными интервалами необходимо рассчитать относительную плотность распределения
 , hi
= h .
(3)
, hi
= h .
(3)
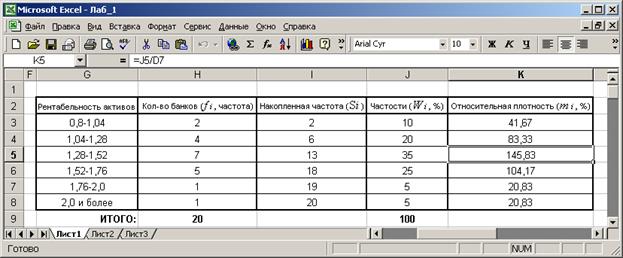
Рис. 3.
4. Необходимо перегруппировать
данные исследуемого интервального вариационного ряда для сопоставления и
анализа двух рядов.
Таблица 2.
|
Группы банков с доходами от 100 до 300 млн. долл.
|
Группы банков с доходами от 50 до 100 млн. долл.
|
|
Рентабельность активов
|
Количество банков в % (частости)
|
Количество банков в % (частости)
|
|
0,6 – 0,8
|
10
|
-
|
|
0,8 – 1,0
|
30
|
8,33 = 0,2m1
|
|
1,0 – 1,1
|
10
|
6,67
|
|
1,1 – 1,2
|
15
|
8,33
|
|
1,2 – 1,4
|
20
|
24,17
|
|
1,4 – 1,8
|
10
|
43,33
=(1,52-1,4)m3+0,24
m4+(1,8-1,76)
m5
|
|
1,8 – 2,0
|
5
|
4,17
|
|
2,0 и более
|
-
|
5,00
|
|
ИТОГО:
|
100
|
100,00
|
Расчетная схема представлена
ниже.
Необходимо вычислить новые
величины интервалов, используя заготовленный рисунок 4:
h01 = y0 – x0 ,
h11 = x1 – y0 ,
h12 = y1 – x1 ,
h21 = x2 – y1 ,
h22 = x3 – x2 ,
h23 = x4 – x3 ,
h24 = y2 – x4 ,
h31 = x5 – y2 ,
h32 = x6 – x5 ,
…
Рис.
Рис. 4.
Здесь – узловые точки
xi рентабельности активов, отстоящие друг от
друга на один и тот же равный шаг h ,
yi – узловые точки интервального ряда
рис. 1 (i = 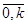 ).
).
На промежутках
[y-1, y0] U [y0, y1]
U [y1, y2] U
[y2, y3]
частости Wi перераспределяются следующим образом:
[y-1, y0] ¾ W0 = h01m1 ,
[y0, y1] ¾ W1 = h11m1 + h12m2
,
[y1, y2] ¾ W2 = h21m2 + h22m3+
h23m4+ h24m5
,
[y2, y3] ¾ W3 = h31m5 + h32m6
,
…
Полученными новыми
значениями Wi заполняется третий столбец таблицы 2.
5. Графическое представление
кривой (ненормированной плотности) распределения исходного ряда рис. 3.
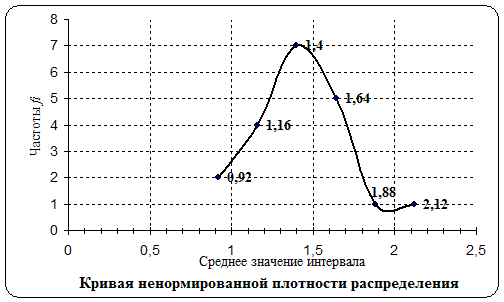
Рис. 5.
6. Полигон частот рис. 6.
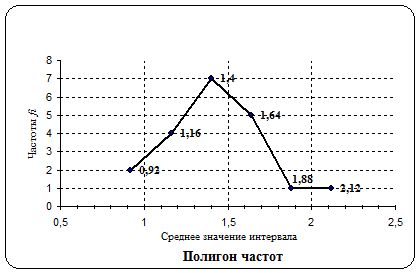
Рис. 6.
7. Гистограмма рис. 7.
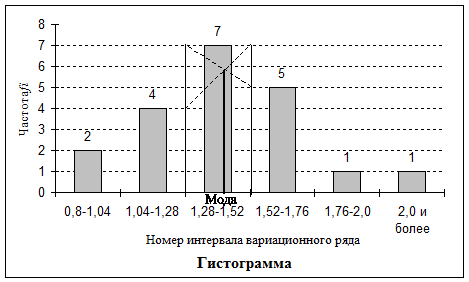
Рис. 7.
8. Кумулятивная кривая накопленных
частот.

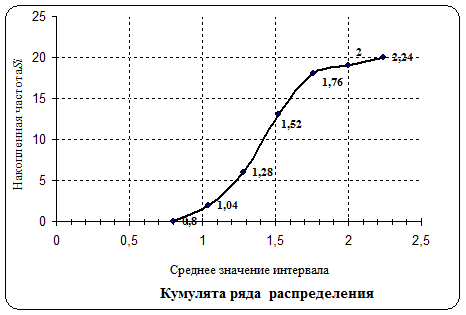
Рис. 8.
9. Сравнительная оценка частот
интервальных вариационных рядов по уровню рентабельности активов банков с доходами
от 100 до 300 млн. долл. и от 50 до 100 млн. долл. (табл. 2).
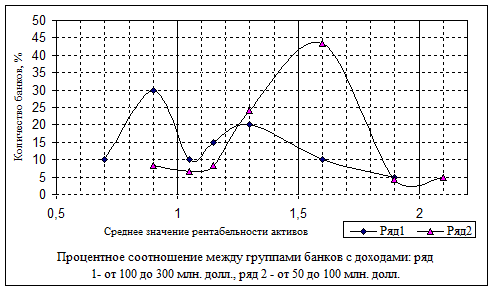
Рис. 9.
Выводы. Количество банков с доходами от 100 до
300 млн. долл. до уровня рентабельности 1,25
больше, чем банков с доходами от 50 до 100 млн. долл. После уровня
рентабельности 1,25 банков с доходами от 50 до 100 млн. долл. значительно
больше, чем банков с доходами от 100 до 300 млн. долл. Экстремальные значения при
рентабельности активов 0,9 имеют 30 % банков с доходами от 100 до 300 млн.
долл. и при рентабельности активов 1,6 имеют 43,33 % банков с доходами от 50 до 100 млн. долл.
Представленная графическая зависимость
позволяет сделать вывод о том, что наиболее рентабельными являются банки ряда 2
(рис. 9).
Варианты заданий. Варианты указаны римскими цифрами.
Сгруппированный
ряд сравнивать с рядом заданным в табл. 1.
Таблица
3.
|
Вар.
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII
|
IX
|
X
|
XI
|
XII
|
XIII
|
XIV
|
XV
|
|
1
|
0,52
|
0,65
|
0,89
|
1,21
|
1,25
|
1,69
|
1,45
|
1,85
|
0,35
|
0,68
|
0,48
|
1,25
|
1,79
|
1,96
|
0,86
|
|
2
|
¾
|
1,63
|
¾
|
1,69
|
1,85
|
¾
|
0,42
|
1,64
|
1,05
|
1,78
|
1,51
|
¾
|
1,11
|
1,54
|
1,88
|
|
3
|
1,22
|
0,53
|
1,29
|
¾
|
1,84
|
0,94
|
1,21
|
¾
|
1,43
|
1
|
0,49
|
1,22
|
1,95
|
1,05
|
1,22
|
|
4
|
1,43
|
1,45
|
¾
|
0,41
|
1,98
|
0,78
|
1,78
|
1,28
|
1,21
|
1,43
|
0,65
|
0,74
|
1,01
|
1,43
|
0,63
|
|
5
|
0,87
|
1,34
|
1,06
|
¾
|
0,89
|
1,21
|
1,54
|
1,78
|
0,73
|
1,11
|
0,85
|
0,65
|
1,54
|
1,73
|
1,64
|
|
6
|
1,55
|
1,68
|
0,69
|
1,75
|
0,95
|
1,54
|
1,66
|
1,37
|
1,25
|
0,74
|
0,53
|
¾
|
1,55
|
1,51
|
1,01
|
|
7
|
¾
|
1,88
|
¾
|
¾
|
1,96
|
0,50
|
1,10
|
¾
|
1,43
|
1,05
|
0,63
|
1,21
|
0,79
|
1,83
|
1,43
|
|
8
|
0,65
|
0,99
|
1,56
|
¾
|
1,43
|
0,65
|
¾
|
0,89
|
¾
|
¾
|
0,25
|
¾
|
0,74
|
¾
|
1,33
|
|
9
|
0,65
|
1,75
|
¾
|
0,54
|
0,97
|
1,05
|
1,25
|
1,51
|
1,14
|
1,22
|
0,68
|
1,54
|
1,43
|
1,42
|
1,21
|
|
10
|
1,89
|
0,59
|
1,75
|
¾
|
1,99
|
1,25
|
1,48
|
1,88
|
1,64
|
¾
|
1,11
|
¾
|
0,95
|
0,63
|
1,69
|
|
11
|
1,14
|
2,10
|
¾
|
1,52
|
1,54
|
2,01
|
1,03
|
1,56
|
0,75
|
0,89
|
0,72
|
1,25
|
0,83
|
1,64
|
0,65
|
|
12
|
0,91
|
1,87
|
0,89
|
0,65
|
1,05
|
0,94
|
1,66
|
1,11
|
0,63
|
1,92
|
1,43
|
2,14
|
1,37
|
0,89
|
1,54
|
|
13
|
1,37
|
1,43
|
0,92
|
¾
|
1,47
|
1,14
|
0,65
|
2
|
¾
|
1,64
|
0,98
|
1,01
|
¾
|
1,78
|
0,89
|
|
14
|
1,43
|
¾
|
1,25
|
1,49
|
1,03
|
¾
|
1,96
|
1,43
|
1,08
|
0,72
|
0,35
|
0,89
|
0,63
|
1,47
|
1,61
|
|
15
|
1,78
|
1,37
|
1,45
|
1,37
|
1,21
|
1,78
|
1,62
|
1,22
|
0,74
|
¾
|
1,78
|
¾
|
1,25
|
1,63
|
1,37
|
|
16
|
0,96
|
0,89
|
1,51
|
0,63
|
1,07
|
0,59
|
1,43
|
1,01
|
1,51
|
1,21
|
0,74
|
0,76
|
1,05
|
1,22
|
1,51
|
|
17
|
1,25
|
1,65
|
1,65
|
¾
|
1,42
|
1,45
|
1,51
|
1,23
|
1,11
|
1,01
|
1,21
|
1,51
|
0,89
|
1,92
|
2
|
|
18
|
1,11
|
1,21
|
1,78
|
1,25
|
1,65
|
1,29
|
1,81
|
¾
|
0,65
|
1,37
|
0,86
|
0,32
|
0,99
|
1,88
|
1,65
|
|
19
|
0,58
|
1,43
|
1,08
|
¾
|
2
|
1,21
|
1,11
|
¾
|
1,88
|
0,63
|
1,05
|
0,63
|
0,69
|
0,74
|
1,51
|
|
20
|
1,56
|
1,52
|
¾
|
1,37
|
1,08
|
1,11
|
1,70
|
1,25
|
1,54
|
1,09
|
0,39
|
¾
|
1,06
|
1,25
|
0,65
|
|
21
|
1,09
|
1,34
|
1,23
|
0,89
|
1,84
|
1,44
|
1,37
|
¾
|
0,85
|
0,78
|
1,89
|
1,54
|
1,56
|
1,75
|
1,11
|
|
22
|
2
|
1,37
|
1,42
|
¾
|
1,54
|
¾
|
1,67
|
0,63
|
0,68
|
1,25
|
0,45
|
1,05
|
1,15
|
1,32
|
1,56
|
|
23
|
1,21
|
1,87
|
¾
|
0,74
|
1,89
|
1,22
|
1,74
|
1,54
|
1,55
|
0,46
|
1,01
|
¾
|
2,12
|
1,62
|
0,74
|
|
24
|
0,99
|
1,25
|
1,67
|
¾
|
1,84
|
1,98
|
1,42
|
1,21
|
0,89
|
1,43
|
1,64
|
1,11
|
1,24
|
1,84
|
1,05
|
|
25
|
1,45
|
¾
|
0,65
|
1,64
|
1,42
|
1,32
|
1,83
|
0,95
|
1,22
|
¾
|
0,89
|
0,85
|
1,88
|
0,65
|
1,78
|
|
26
|
0,89
|
1,47
|
1,58
|
1,57
|
1,37
|
0,89
|
1,06
|
0,97
|
¾
|
0,67
|
1,05
|
0,81
|
1,25
|
1,74
|
1,37
|
|
27
|
¾
|
1,14
|
1,02
|
1,58
|
1,65
|
1,64
|
1,43
|
1,25
|
1,21
|
1,54
|
0,81
|
1,43
|
1,13
|
1,71
|
1,64
|
|
28
|
1,87
|
1,35
|
¾
|
1,78
|
1,24
|
¾
|
1,59
|
1,05
|
0,71
|
1,51
|
1,22
|
1,85
|
1,22
|
1,21
|
1,25
|
|
29
|
0,62
|
1,11
|
1,79
|
¾
|
¾
|
1,42
|
1,04
|
0,74
|
1,78
|
¾
|
1,54
|
0,93
|
1,51
|
1,01
|
1,35
|
|
30
|
1,23
|
1,02
|
1,21
|
1,85
|
1,06
|
1,56
|
0,89
|
1,28
|
1,05
|
0,65
|
0,41
|
0,89
|
0,69
|
1,65
|
1,74
|