Постановка задачи

Корреляционно-регрессионный анализ (КР-анализ) взаимосвязи признаков является составной частью проводимого статистического исследования двух экономических показателей статистической совокупности 32 предприятий и частично использует результаты Лабораторной работы №1.

В лабораторной работе №2 изучается взаимосвязь между факторным признаком Среднегодовая стоимость основных производственных фондов (признак Х) и результативным признаком Выпуск продукции (признак Y), значениями которых являются исходные данные Лабораторной работы №1 после исключения из них аномальных значений.

Таблица 1

Исходные данные

Номер предприятия

Среднегодовая стоимость основных производственных фондов, млн. руб.

Выпуск продукции, млн. руб.

1

4256,00

4068,50

2

5006,50

4463,50

3

5164,50

4977,00

4

5441,00

5530,00

5

3545,00

2765,00

6

5717,50

4740,00

7

5875,50

6399,00

8

4414,00

4345,00

9

5401,50

5095,50

10

6231,00

6359,50

11

6823,50

6715,00

13

5204,00

5293,00

14

5717,50

5767,00

15

6547,00

6991,50

16

7495,00

7505,00

17

5599,00

5056,00

18

6191,50

6004,00

19

4927,50

3752,50

20

6270,50

5135,00

21

6981,50

6912,50

22

4809,00

3910,50

23

3821,50

3673,50

24

6389,00

5885,50

25

5717,50

5135,00

26

5322,50

4858,50

27

4137,50

3160,00

28

5559,50

4937,50

29

6428,50

5411,50

30

6112,50

5135,00

32

4493,00

4582,00

В процессе статистического исследования необходимо решить ряд задач.

1.Установить наличие статистической связи между факторным признаком Х и результативным Y:

a)     Графическим методом;

b)    Методом сопоставления параллельных рядов.

2.Установить наличие корреляционной связи между признаками Х и Y методом аналитической группировки.

3.Оценить тесноту связи признаков Х и Y на основе:

a)     Эмпирического корреляционного отношения η;

b)    Линейного коэффициента корреляции r.

4.Построить однофакторную линейную регрессионную модель связи признаков Х и Y, используя инструмент регрессия надстройки Пакет анализа.

5. Оценить адекватность и практическую пригодность построенной линейной регрессионной модели, указав:

а)     Доверительные интервалы коэффициентов ;

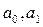б)    Степень тесноты связи признаков Х и Y;

в)     Погрешность регрессионной модели.

6) Дать экономическую интерпретацию:

а)     Коэффициента регрессии ;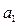

б)    Коэффициента эластичности ;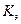

в)     Остаточных величин .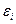

7. Найти наиболее адекватное нелинейное уравнение регрессии с помощью средств инструмента Мастер диаграмм. Построить для этого уравнения теоретическую кривую регрессии.

Отчётность по работе:

Результативные таблицы и графики:

Таблица 2

Зависимость выпуска продукции от среднегодовой стоимости

 основных фондов

Номер группы

Группы предприятий по стоимости основных фондов

Число предприятий

Выпуск продукции

Всего

В среднем на одно предприятие

1

3545 - 4335

4

346,00

86,50

2

4335 - 5125

5

533,00

106,60

3

5125 - 5915

11

1 463,00

133,00

3

5915 - 6705

7

1 036,00

148,00

5

6705 - 7495

3

535,00

178,33

Итого:

30

3 913,00

130,43

Таблица 3

Показатели внутригрупповой вариации

Номер группы

Группы предприятий по стоимости основных фондов

Число предприятий

Внутригрупповая дисперсия

1

3545 - 4335

4

157,25

2

4335 - 5125

5

66,64

3

5125 - 5915

11

135,6363636

4

5915 - 6705

7

256,5714286

5

6705 - 7495

3

72,22222222

Итого

30

688,3200144

Таблица 4

Показатели дисперсии и эмпирического

 корреляционного отношения

Общая дисперсия

Средняя из внутригрупповых дисперсий

Межгрупповая дисперсия

Эмпирическое корреляционное отношение

804,7788889

148,8955556

655,8833333

0,902765617

Таблица.5

Линейный коэффициент корреляции признаков

Столбец 1

Столбец 2

Столбец 1

1

Столбец 2

0,91318826

1

Выходные таблицы

Таблица 6

ВЫВОД ИТОГОВ

Регрессионная статистика

Множественный R

0,91318826

R-квадрат

0,833912798

Нормированный R-квадрат

0,827981112

Стандартная ошибка

11,96707419

Наблюдения

30

Таблица 7

Дисперсионный анализ

df

SS

MS

F

Значимость F

Регрессия

1

20133,46245

20133,46245

140,5861384

1,97601E-12

Остаток

28

4009,904212

143,2108647

Итого

29

24143,36667

Таблица 8

 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Y-пересечение

-11,18284019

12,14197063

-0,92100702

0,364914527

Переменная X 1

1,089355181

0,09187519

11,85690257

1,97601E-12

Y-пересечение

Нижние 95%

Верхние 95%

Нижние 68,3%

Верхние 68,3%

 

Переменная X 1

-36,05456748

   13,68889

-23,5536

1,187938

 

0,901157173

1,277553

0,995749

1,182962

 

Таблица 9

ВЫВОД ОСТАТКА

Наблюдение

Предсказанное Y

Остатки

1

75,96557429

-5,965574286

2

83,59106055

9,408939448

3

92,305902

-12,305902

4

95,57396754

7,426032457

5

99,93138827

10,06861173

6

102,1100986

13,88990137

7

110,8249401

-11,82494008

8

114,0930056

-19,09300562

9

116,271716

-3,271715981

10

120,6291367

5,370863295

11

121,7184919

12,28150811

12

124,9865574

-1,986557429

13

127,1652678

1,83473221

14

128,254623

11,74537703

15

131,5226885

-6,522688514

16

132,6120437

-4,612043695

17

135,8801092

-15,88010924

18

135,8801092

10,11989076

19

135,8801092

-5,880109238

20

140,23753

21,76247004

21

146,773661

-16,77366105

22

148,9523714

3,047628591

23

150,0417266

10,95827341

24

151,1310818

-21,13108177

25

154,3991473

-5,399147314

26

155,4885025

-18,4885025

27

158,756568

18,24343196

28

166,3820543

3,617945695

29

170,739475

4,260524972

30

184,9010924

5,098907619

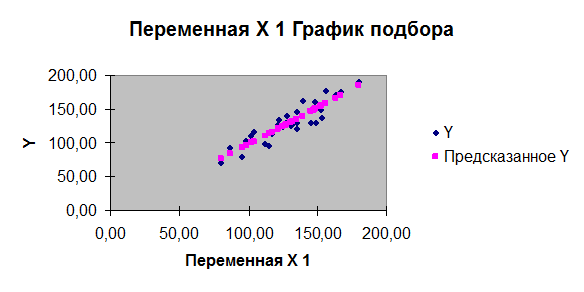
                                                          рисунок 1.

                                                         

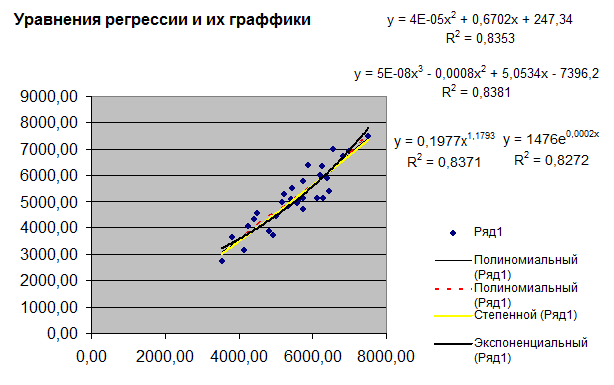
рисунок 2.

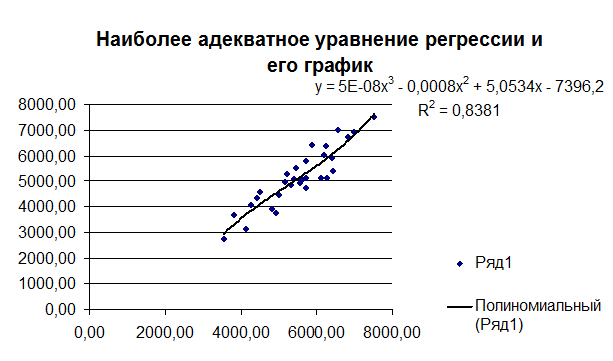
рисунок 3.

Выводы по результатам лабораторной работы

Задание 1. Наличие статистических взаимосвязей признаков устанавливается на основе теоретического анализа. Для выявления наличия статистических связей между факторным признаком Х (Среднегодовая стоимость основных производственных фондов) и результативным признаком Y (выпуск продукции) применяются разнообразные статистические методы:

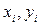а) Графический метод состоит в построении корреляционного поля – множества точек ( ). По характеру расположения точек корреляционного поля можно сделать вывод о наличии или отсутствии связи. В нашем случае точки группируются вокруг некоторой определённой линии, то есть возле линии регрессии (рисунок 3). Анализируя данные рисунка 3. видно, что точки ( ) не лежат на одной линии, но всё же их расположение обнаруживает определённую тенденцию, которая выражается видом эмпирической линии связи. Эта линия связи (рисунок 3) по своему виду приближается к прямой линии, то есть связи между факторным признаком Х (Среднегодовая стоимость основных производственных фондов) и результативным признаком Y (выпуск продукции) линейная прямая.

б) Метод сопоставления параллельных рядов заключается в выявлении статистической связи путём простого параллельного сравнения факторных и результативных значений.  Для этого, значения фактора Х ранжируется (таблица 10).                                                                                          Таблица 10

Ранжирование по возрастанию признака

«Среднегодовая стоимость производственных фондов»

Номер предприятия

Среднегодовая стоимость основных производственных фондов, млн. руб.

Выпуск продукции, млн. руб.

5

3545,00

2765,00

23

3821,50

3673,50

27

4137,50

3160,00

1

4256,00

4068,50

8

4414,00

4345,00

32

4493,00

4582,00

22

4809,00

3910,50

19

4927,50

3752,50

2

5006,50

4463,50

3

5164,50

4977,00

13

5204,00

5293,00

26

5322,50

4858,50

9

5401,50

5095,50

4

5441,00

5530,00

28

5559,50

4937,50

17

5599,00

5056,00

6

5717,50

4740,00

14

5717,50

5767,00

25

5717,50

5135,00

7

5875,50

6399,00

30

6112,50

5135,00

18

6191,50

6004,00

10

6231,00

6359,50

20

6270,50

5135,00

24

6389,00

5885,50

29

6428,50

5411,50

15

6547,00

6991,50

11

6823,50

6715,00

21

6981,50

6912,50

16

7495,00

7505,00

Из таблицы видно, что с возрастанием значений признака «Среднегодовая стоимость основных производственных фондов» значения признака «Выпуск продукции» также в целом возрастают при наличии некоторых отклонений от этой общей тенденции, то можно сделать вывод о том, что между признаками Х и Y возможно наличие прямой корреляционной связи.

Задание 2. При выявлении наличия связи методом аналитической группировки строится аналитическая таблица (таблица 2), отражающая результаты аналитической группировки единиц совокупности по факторному признаку Х (Среднегодовая стоимость основных производственных фондов). Анализируя данные таблицы 2, можно заметить, что при переходе от одной группы к другой средние значения признака «Выпуск продукции» изменяются с определённой закономерностью, то есть возрастают. Это говорит о том, что между признаком Х (Среднегодовая стоимость основных производственных фондов) и результативным признаком Y (выпуск продукции) существует корреляционная связь.

Задание 3. а) Для анализа тесноты связи признаков Х и Y рассчитан показатель эмпирического корреляционного отношения η (таблица 4). Для показателей силы и тесноты корреляционной связи характерно следующее свойство:

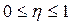
Чем ближе значение показателя к единице, тем теснее связь и больше сила связи. В нашем случае  η = 0,902, то есть значение показателя ближе к единице, то это говорит о тесной и сильной связи между признаками.

б) Оценить тесноту связи можно и с помощью  линейного коэффициента корреляции r. Для качественной оценки тесноты связи используется Шкала Чэддока:

Значения показателей тесноты связи r:         Характеристика связи:

0.1 – 0.3                                                                      слабая

0,3 – 0,5                                                                   умеренная

0.5 – 0,7                                                                     заметная

0,7 – 0,9                                                                    высокая

0,9 – 0,99                                                             весьма высокая

Исходя из данных таблицы 5,  линейный коэффициент корреляции

r = 0, 91318826. то есть связь между признаками весьма высокая.

Задание 4. Регрессионный анализ заключается в определении аналитического выражения связи между факторным признаком Х и результативным признаком Y.

В случае линейной формы связи построение модели средствами Excel осуществляется с помощью инструмента Регрессия надстройки Пакет анализа.

В результате работы инструмента  Регрессия Excel формирует следующий        набор таблиц.

1. Таблица Регрессионная статистика (таблица 6).

2. Таблица Дисперсионный анализ (таблица 7).

3. Результативная таблица (таблица 8).

4. Таблица Вывод остатка (таблица 9).

Задание 5. Проверка адекватности регрессионной модели фактическим данным наблюдения осуществляется путем оценки тесноты связи между факторными значениями Х и выровненными результативными значениями  Y.

а) Доверительные интервалы построенной регрессионной модели для коэффи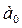циента , рассчитанные для уровня надежности Р=0,95 от 0,901157173 до 1,277553, рассчитанные для уровня надежности Р=0,683 от  0,995749 до 1,182962. Доверительные интервалы коэффициента 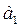  при Р=0,95 от -36,05456748 до 13,68889, при Р=0,683 от -23,5536 до 1,187938.

б) Для построенной регрессионной модели измерение тесноты связи признаков Х и Y осуществляется на основе R – индекса корреляции. Индекс корреляции R принимает значения в пределах 0≤R≤1. Близость индекса корреляции к единице означает, что связь между признаками достаточно хорошо описывается избранным уравнением корреляционной зависимости.

в) В качестве критерия адекватности регрессионной модели  используются показатели:

- средняя квадратическая ошибка уравнения регрессии 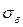,представляющая собой среднее квадратическое отклонение эмпирических значений признака Y от теоретических;

- средняя ошибка аппроксимации 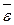, выражающая в процентах меру отклонения расчетных значений Y от фактических.

В адекватных моделях ошибки не должны превышать 12-15%, в нашем случае стандартная ошибка равна 11,96707419, то есть модель наиболее адекватная.

Задание 6. Экономическая интерпретация построенной регрессионной модели взаимосвязи признаков используется для целей анализа и прогноза взаимосвязей признаков.

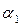а) Величина коэффициента регрессии показывает, насколько в среднем (в абсолютном выражении) изменяется значение результативного признака Y при изменении фактора Х на единицу его измерения. В моем случае коэффициент регрессии 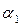 =1,089355181, то есть на 1,089355181 в среднем  изменяется значение результативного признака Y при изменении фактора Х на единицу его измерения.  

б) с целью расширения возможностей экономического анализа используется коэффициент эластичности 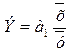, который показывает, на сколько процентов изменяется в среднем результативный признак при изменении факторного признака на 1%. Э = 1,167%, то есть на 1,67% изменяется в среднем результативный признак при изменении факторного признака на 1%.

в) анализируя остатки 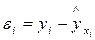, характеризующие отклонения i-х наблюдений от значений 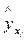, которые следует ожидать в среднем, можно сделать ряд практических выводов об эффективности экономической деятельности рассматриваемых хозяйствующих субъектов и выявить скрытые резервы их развития и повышения деловой активности. При этом наиболее значительный экономический интерес представляют собой наибольшие и наименьше положительные и отрицательные отклонения  .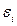

Задание 7.

С помощью средств инструмента Мастер диаграмм была построена однофакторная нелинейная регрессионная модель. В результате на диаграмме рассеяния отображается линия и уравнение регрессии, а также коэффициент детерминации 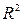 (рис. 2). Выбор наиболее адекватного уравнения нелинейной регрессии определяется максимальным значением коэффициента 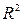 (рис. 3).   

Таблица 2.1

Исходные данные

Номер предприятия

Среднегодовая стоимость основных производственных фондов, млн. руб.

Выпуск продукции, млн. руб.

1

98,00

103,00

2

117,00

113,00

3

121,00

126,00

4

128,00

140,00

5

80,00

70,00

6

135,00

120,00

7

139,00

162,00

8

102,00

110,00

9

127,00

129,00

10

148,00

161,00

11

163,00

170,00

13

122,00

134,00

14

135,00

146,00

15

156,00

177,00

16

180,00

190,00

17

132,00

128,00

18

147,00

152,00

19

115,00

95,00

20

149,00

130,00

21

167,00

175,00

22

112,00

99,00

23

87,00

93,00

24

152,00

149,00

25

135,00

130,00

26

125,00

123,00

27

95,00

80,00

28

131,00

125,00

29

153,00

137,00

30

145,00

130,00

32

104,00

116,00