Всероссийский Заочный Финансово-Экономический Институт
Контрольная работа по дисциплине «Эконометрика»
Вариант №10
Преподаватель: Гармаш
А.Н.
Москва, 2006 г.
Задача 1
По
предприятиям легкой промышленности региона получена информация, характеризующая
зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (X, млн. руб.).
Требуется:
1. Найти
параметры уравнения линейной регрессии, дать экономическую интерпретацию
коэффициента регрессии.
2. Вычислить
остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 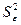 ; построить график остатков.
; построить график остатков.
3. Проверить
выполнение предпосылок МНК.
4. Осуществить
проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (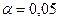 ).
).
5. Вычислить
коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (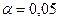 ), найти среднюю относительную ошибку аппроксимации. Сделать
вывод о качестве модели.
), найти среднюю относительную ошибку аппроксимации. Сделать
вывод о качестве модели.
6. Осуществить
прогнозирование среднего значения показателя Y при уровне значимости 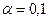 , если прогнозное значение фактора X составит 80% от его максимального
значения.
, если прогнозное значение фактора X составит 80% от его максимального
значения.
7. Представить
графически: фактические и модельные значения Y, точки прогноза.
8. Составить
уравнения нелинейной регрессии:
∙
гиперболической;
∙
степенной;
∙
показательной.
Привести
графики построенных уравнений регрессии.
9. Для
указанных моделей найти коэффициенты детерминации и средние относительные
ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.
Данные для
расчетов представлены в таблице 1.
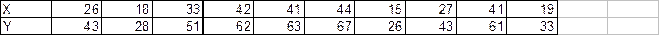
Решение:
1. Найти
параметры уравнения линейной регрессии, дать экономическую оценку коэффициента
регрессии.
Уравнение
(модель) линейной регрессии имеет вид: 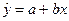 .
.
Параметры a и b можно оценить методом наименьших
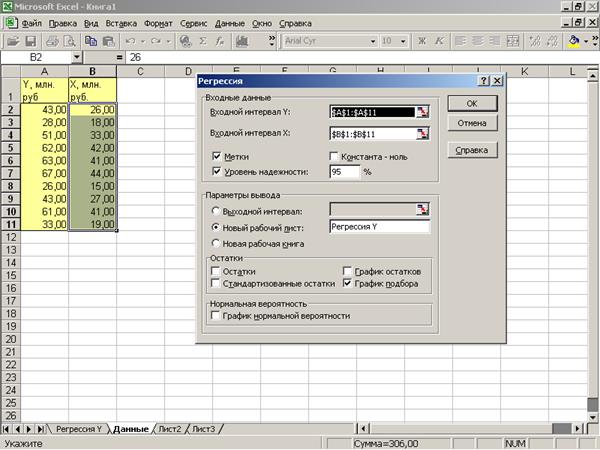
квадратов. Для автоматизации расчетов используем программу РЕГРЕССИЯ
статистического пакета «Анализ данных» MS Excel (Приложение 1).
Полученные коэффициенты a и b запишем в уравнение линейной
регрессии: 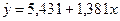
Коэффициент
регрессии b=1,381
показывает, что с увеличением объема капиталовложений X на 1 млн. руб. объем выпуска продукции
Y в среднем увеличится
на 1,381 млн. руб.
2.
Вычислить остатки, найти остаточную сумму квадратов, оценить дисперсию
остатков, построить график остатков.
Остатки
рассчитываются по формуле:
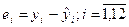
В данной
задаче остатки рассчитаны в таблице MS Excel (Приложение 2).
Остаточная
сумма квадратов определяется с помощью функции СУММКВ.
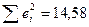
Дисперсия
остатков вычисляется с помощью функции ДИСП = 1,62 (Приложение 3).
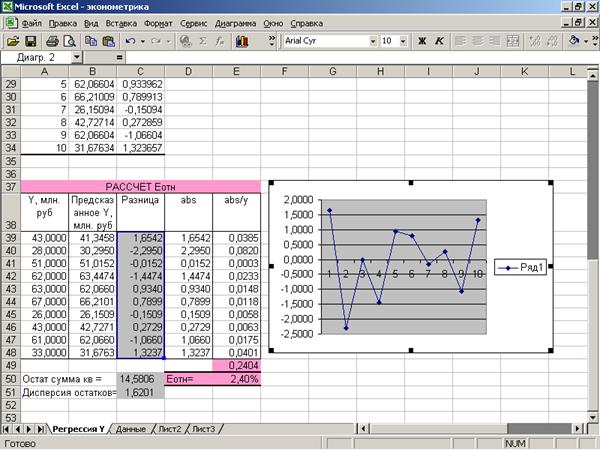
Для
построения графика остатков используется Мастер диаграмм (Приложение 4).
3.
Проверить выполнение предпосылок МНК (оценить адекватность модели).
Для оценки
адекватности модели исследуют остатки 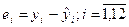 .
.
Исследование
остатков предполагает проверку наличия у них следующих пяти свойств
(предпосылок МНК):
а. Нулевая
(или близкая к ней) средняя величина остатка.
б. Случайность
характера остатка.
в.
Независимость (отсутствие автокорреляции) остатков.
г.
Соответствие ряда остатков нормальному закону распределения.
д.
Гомоскедастичность (постоянство) дисперсии остатков.
А.
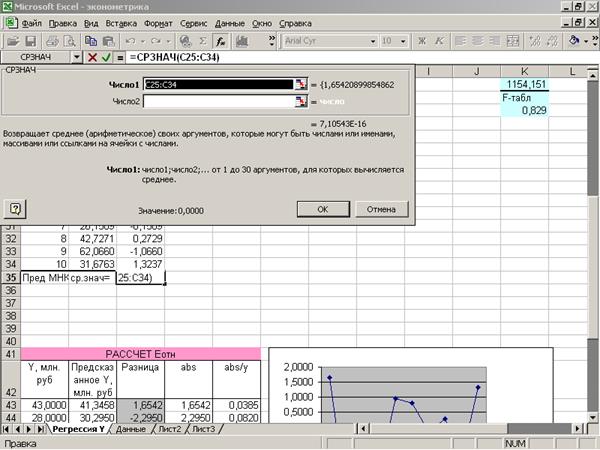
Для
вычисления среднего значения остатка используем функцию СРЗНАЧ (Приложение 5).
В данной
задаче 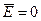 , поэтому первое свойство остатков выполняется.
, поэтому первое свойство остатков выполняется.
Б.
Для проверки
случайности остатков используем критерий поворотных точек. Анализируя
построенный график остатков делаем вывод, что в этой задаче число поворотных
точек р=8. В случайном ряду чисел должно выполняться строгое неравенство:
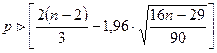 при n=10
при n=10
В нашем
случае p=8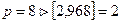 , т.е. свойство случайности остатков выполняется.
, т.е. свойство случайности остатков выполняется.
В.
При проверке
независимости (отсутствия автокорреляции) используется коэффициент
автокорреляции 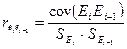 .
.
Для расчета
автокорреляции используется стандартная функция КОРРЕЛ(С25-С33;С26-С34)=
-0,5349 (Приложение 6).
Оценим
значимость полученного коэффициента автокорреляции с использованием t-критерия:
Расчетное
значение t-критерия: 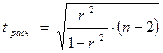 =1,79 (расчет выполнен средствами Excel).
=1,79 (расчет выполнен средствами Excel).
Табличное
значение t-статистики
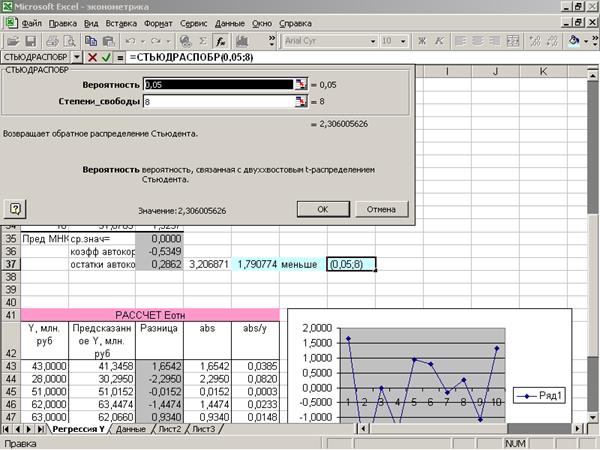
определяется с помощью функции СТЬЮДРАСПОБР(0,05;8)=2,306 (Приложение 7).
Поскольку
расчетное значение t-критерия
меньше табличного, то коэффициент автокорреляции незначим, т.е. остатки не
автокоррелированы. Свойства независимости остатков выполняется.
Модель в
целом адекватна.
Г.
Соответствие
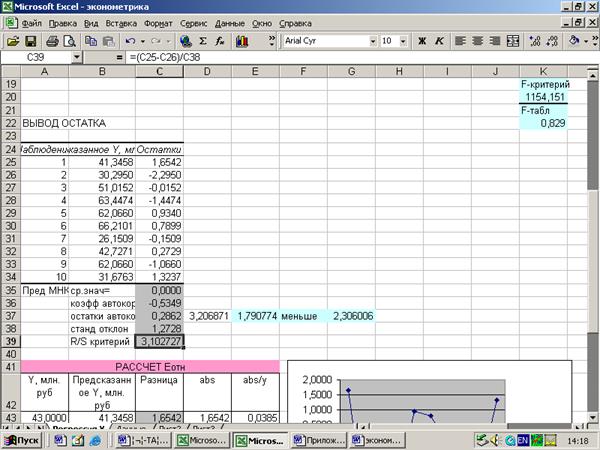
ряда остатков нормальному закону распределения определяется при помощи R/S-критерия.
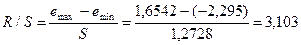 (Приложение 8).
(Приложение 8).
Полученное
значение этого критерия попадает между табулированными границами (2,67-3,57) с
заданным уровнем значимости (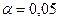 ) и n=10, таким образом, свойство нормальности остатков
выполняется.
) и n=10, таким образом, свойство нормальности остатков
выполняется.
Д.
Чтобы оценить
нарушение гомоскедастичности по тесту Гольдфельда-Кванта необходимо выполнить
следующие шаги:
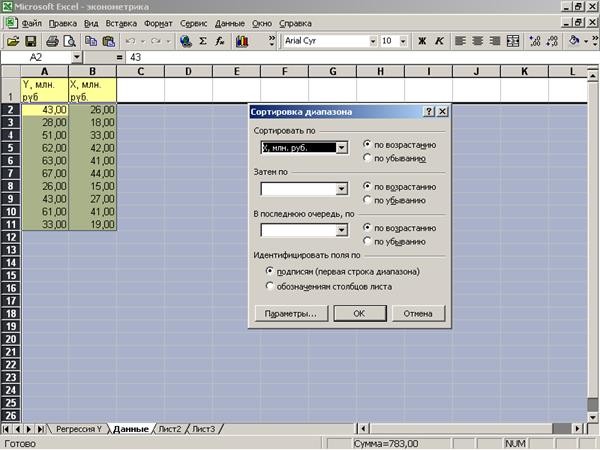
1) Упорядочение
n наблюдений по мере
возрастания переменной Х (Приложение 9);
2) Разделение
совокупности на две группы соответственно с малыми и большими значениями
фактора Х, определение по каждой из групп уравнений регрессии. Разделение на
две группы по фактору Х примет вид:
|
1
|
|
2
|
|
Y,
млн. руб
|
Х,
млн. руб.
|
|
Y,
млн. руб
|
Х,
млн. руб.
|
|
26,00
|
15,00
|
|
51,00
|
33,00
|
|
28,00
|
18,00
|
|
63,00
|
41,00
|
|
33,00
|
19,00
|
|
61,00
|
41,00
|
|
43,00
|
26,00
|
|
62,00
|
42,00
|
|
43,00
|
27,00
|
|
67,00
|
44,00
|
Выполнив в Excel функцию РЕГРЕССИЯ для каждой
группы получим уравнения регрессии:
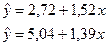
3) Определение
остаточной суммы квадратов для первой и второй регрессий. С помощью функции
СУММКВ получим: для первой регрессии СУММКВ=7,663, для второй 4,596.
4) Вычисление
расчетного значения F-статистики.
7,663/4,596=1,667.
5) Вычисление
табличного значения F-статистики,
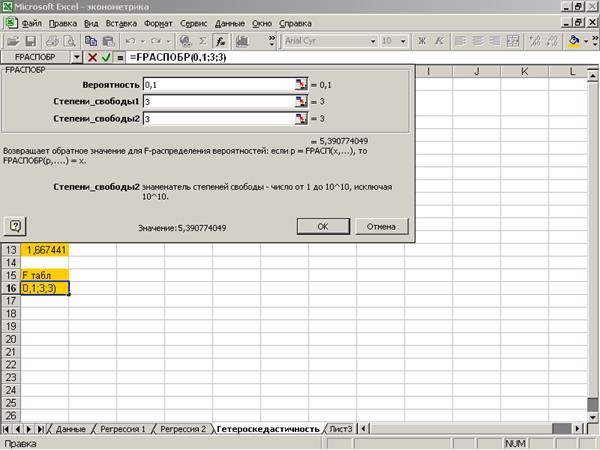
которое производится при помощи функции FРАСПОБР (Приложение 10). 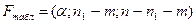 , где
, где 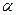 =0,1.
=0,1. 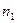 =5, m=2,
n=10.
=5, m=2,
n=10.
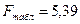
Значение F-расчетного меньше F-табличного, что свидетельствует о том,
что гетероскедастичность не обнаружена и, следовательно, выполняются свойства
гомоскедастичности остатков.
Оценка адекватности модели
выполнена.
Построенная модель является адекватной реальному процессу, её можно
использовать для построения прогнозных оценок.
4.
Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (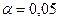 ).
).
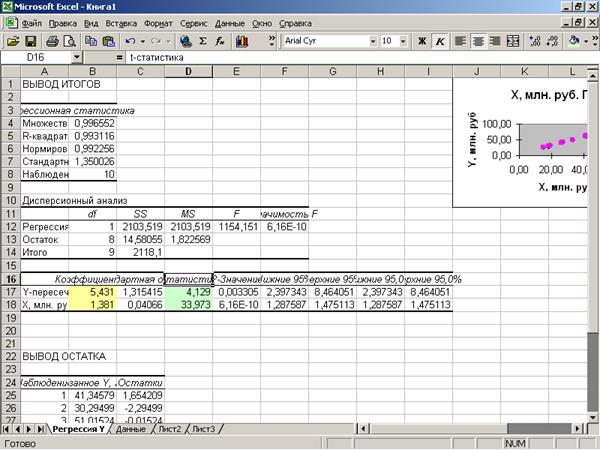
Для оценки
статистической значимости параметров полученной модели используем t-критерий. Расчетное
значение t-статистики
определяется по формулам (Приложение 11):
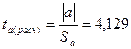 ;
;
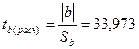 .
.
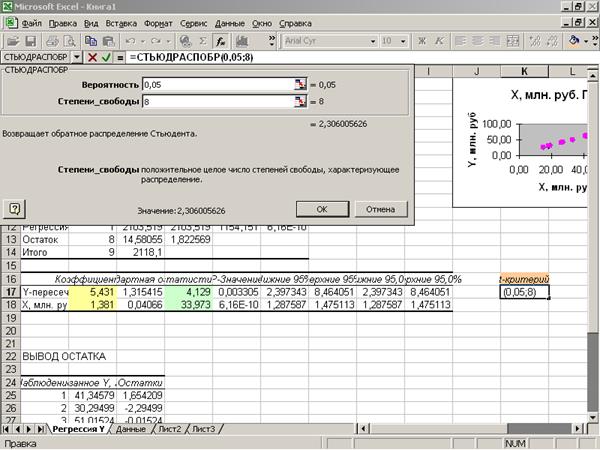
Табличное
значение t-критерия
можно определить с помощью функции СТЬЮДРАСПОБР(0,05;8)=2,306 (Приложение 12).
Поскольку 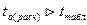 , то параметр а статистически значим.
, то параметр а статистически значим.
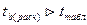 , следовательно, параметр b статистически значим, существенно отличается от 0.
, следовательно, параметр b статистически значим, существенно отличается от 0.
5.
Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с
помощью F-критерия
Фишера (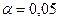 ), найти среднюю относительную ошибку аппроксимации. Сделать
вывод о качестве модели.
), найти среднюю относительную ошибку аппроксимации. Сделать
вывод о качестве модели.
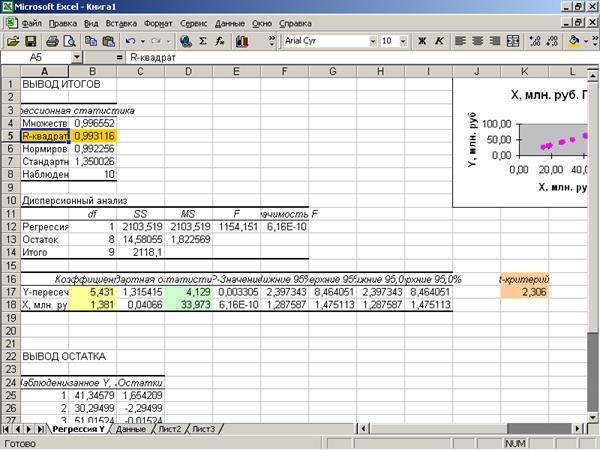
Коэффициент
детерминации 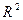 можно, например, определить по формуле:
можно, например, определить по формуле:
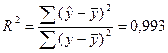 (Приложение 13).
(Приложение 13).
Таким
образом, все вариации в объеме выпуска продукции Y на 99,3% обусловлены вариацией в
объеме капиталовложений X,
т.е. изменениями в факторе X,
учтенном в модели.
Соответственно,
все изменения в Y на
0,7 % обусловлены изменениями факторов, неучтенных в модели.
Оценка
значимости уравнения регрессии проводится с помощью F-критерия. Расчетное значение F-критерия в нашем случае
определяется по формуле:
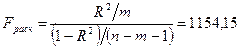
Табличное
значение F-критерия
определяется с помощью функции FРАСП
(Приложение 14).
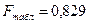
Поскольку
расчетное значение F-критерия
Фишера больше табличного, то уравнение регрессии признается значимым,
соответствующим фактическим данным.
Находим
среднюю относительную ошибку аппроксимации (Приложение 15):
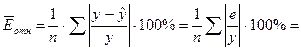 2,4%
2,4%
Таким
образом, модельные значения  отклоняются от фактических значений Y в среднем на 2,4%, т.е. получена
модель хорошего качества, высокой точности).
отклоняются от фактических значений Y в среднем на 2,4%, т.е. получена
модель хорошего качества, высокой точности).
6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости 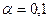 , если прогнозное значение фактора Х составит 80% от его
максимально значения.
, если прогнозное значение фактора Х составит 80% от его
максимально значения.
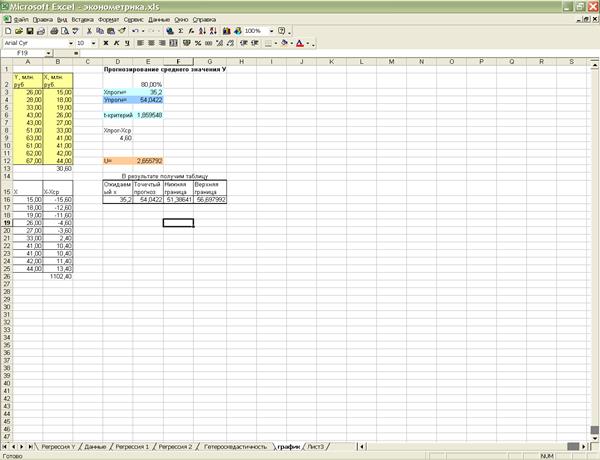
Х прогн=44*0,8=35,2
Y
прогн=5,431+1,381*35,2=54,05
Коэффициент Стьюдента 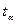 для 8 степеней свободы
и на уровне значимости
для 8 степеней свободы
и на уровне значимости 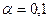 рассчитывается при
помощи функции СТЬЮДРАСПОБР(0,1;8)=1,8595.
рассчитывается при
помощи функции СТЬЮДРАСПОБР(0,1;8)=1,8595.
Отклонение от линии регрессии рассчитывается по формуле: 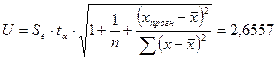 , где Se=1,350
(см. значение «Стандартная ошибка»).
, где Se=1,350
(см. значение «Стандартная ошибка»).
Вычислив величину отклонения от линии регрессии можно найти
доверительный интервал, в котором ожидается появление прогнозируемого среднего
значения Y=54,05:
границы задаются интервалом 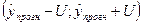 . Интервал в данной задаче: (51,386;56,697).
. Интервал в данной задаче: (51,386;56,697).
Расчет произведен при использовании MS Excel (Приложение 16).
7. Представить графически: фактические и модельные значения Y, точки прогноза.
Строим график «Линейная регрессия»: скопируем в лист с вычислениями
прогнозируемых значений график подбора с листа «Регрессия Y». Соединим точки графика отрезками
(активировать курсором точки – тип данных – отрезки).
Переименовываем график подбора в «Линейную регрессию». К существующим
данным добавляем новые (Исходные данные – Ряд – Добавить): для точечного
прогноза, нижней и верхней границ прогноза, указывая соответствующие данные
(Приложение 17).
8.
Составить уравнения гиперболической (а), степенной (б), показательной (в)
нелинейной регрессий. Построить графики построенных уравнений регрессии.
а)
гиперболическая
Модель гиперболической регрессии имеет вид: 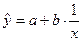
Приведем эту модель к линейному виду осуществив замену переменных: 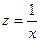 . Получим линейное уравнение вида
. Получим линейное уравнение вида 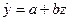 . С помощью функции РЕГРЕССИЯ получим значения a=83,340 и b=-947,945 и модель вида
. С помощью функции РЕГРЕССИЯ получим значения a=83,340 и b=-947,945 и модель вида 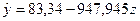 .
.
Т.е. модель гиперболической регрессии имеет вид 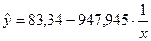
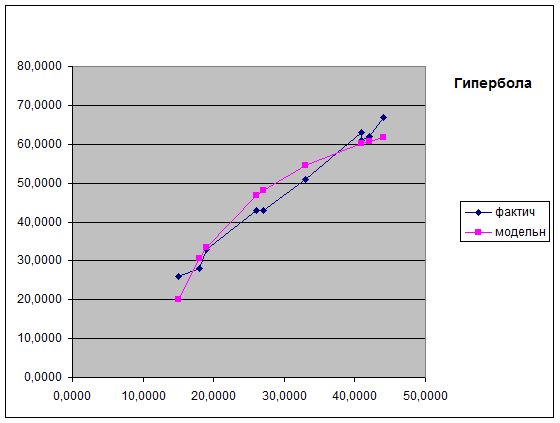
Построим вспомогательные таблицы и с помощью Мастера диаграмм построим модель гиперболической регрессии в
MS Excel.
б)
степенная
Модель степенной регрессии имеет вид: 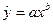
Осуществим линеализацию модели. Прологарифмируем уравнение, получим 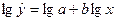 . Представим, что
. Представим, что 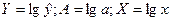 . Тогда получим линейную модель
. Тогда получим линейную модель 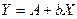
С помощью функции MS Excel
составим дополнительные таблицы для расчета и используем функцию РЕГРЕССИЯ для
нахождения параметров a
и b. Получим А=0,376, a=2,377, b=0,879 и, следовательно, модель
степенной регрессии вида 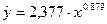
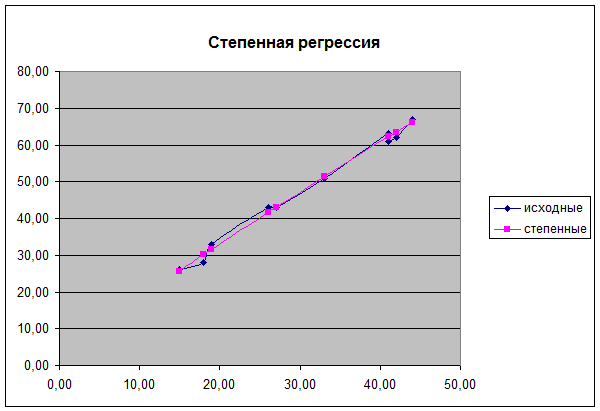
Найдем теоретическое значение y, построим график степенной регрессии при использовании функции
Мастер диаграмм.
в)
показательная
Уравнение показательной кривой 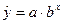
Линеализируем переменные:
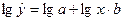 Введем обозначения:
Введем обозначения: 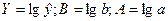 , получим
, получим 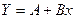
Найдем значение Y=lg y, с помощью функции
РЕГРЕССИЯ найдем параметры А=1,2404, В=0,0135. Тогда модель показательной
регрессии примет вид 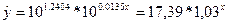
Найдем теоретическое значение y, построим график степенной регрессии при использовании функции
Мастер диаграмм.
9. Для указанных моделей найти коэффициенты детерминации и средние
относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и
сделать вывод.
а) гиперболическая
Рассчитаем характеристики точности модели (Приложение 18).
Индекс детерминации: 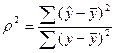 =0,9367
=0,9367
Таким
образом, все вариации в объеме выпуска продукции Y на 93,67% обусловлены вариацией в
объеме капиталовложений X,
т.е. изменениями в факторе X,
учтенном в модели.
Соответственно,
все изменения в Y на
6,33% обусловлены изменениями факторов, неучтенных в модели.
Средняя относительная ошибка аппроксимации: 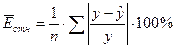 =7,72%
=7,72%
Таким
образом, модельные значения 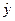 отклоняются от фактических значений Y в среднем на 7,72 %, т.е. получена
модель среднего качества.
отклоняются от фактических значений Y в среднем на 7,72 %, т.е. получена
модель среднего качества.
б) степенная
Рассчитаем характеристики точности модели (Приложение 19).
Индекс детерминации: 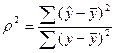 =0,994
=0,994
Таким
образом, все вариации в объеме выпуска продукции Y на 99,4% обусловлены вариацией в
объеме капиталовложений X,
т.е. изменениями в факторе X,
учтенном в модели.
Соответственно,
все изменения в Y на
0,6% обусловлены изменениями факторов, неучтенных в модели.
Средняя относительная ошибка аппроксимации: 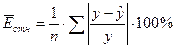 =2,4%
=2,4%
Таким
образом, модельные значения 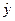 отклоняются от фактических значений Y в среднем на 2,4 %, т.е. получена
модель хорошего качества, высокой точности.
отклоняются от фактических значений Y в среднем на 2,4 %, т.е. получена
модель хорошего качества, высокой точности.
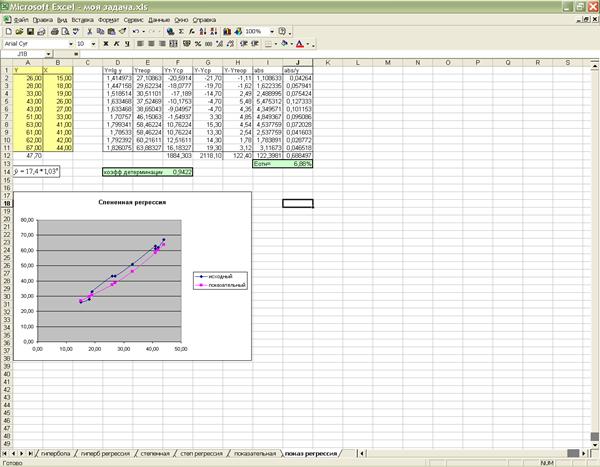
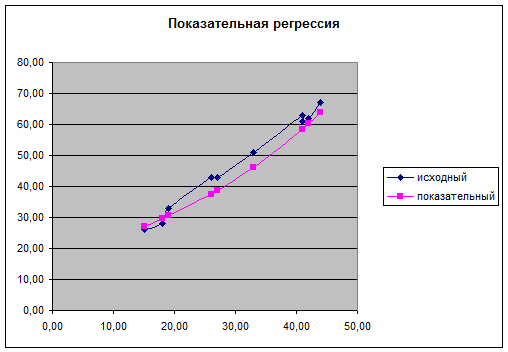
в) показательная
Рассчитаем характеристики точности модели (Приложение 20).
Индекс детерминации: 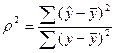 =0,9422
=0,9422
Таким
образом, все вариации в объеме выпуска продукции Y на 94,2% обусловлены вариацией в
объеме капиталовложений X,
т.е. изменениями в факторе X,
учтенном в модели.
Соответственно,
все изменения в Y на
5,8% обусловлены изменениями факторов, неучтенных в модели.
Средняя относительная ошибка аппроксимации: 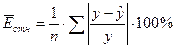 =6,88%
=6,88%
Таким
образом, модельные значения 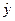 отклоняются от фактических значений Y в среднем на 6,88%, т.е. получена
модель среднего качества.
отклоняются от фактических значений Y в среднем на 6,88%, т.е. получена
модель среднего качества.
Сравнение полученных
моделей
Для сравнения моделей используем полученные данные. Построим таблицу:
|
|
коэфф
детерминации
|
средняя
относительная ошибка
|
|
линейная
|
0,9931
|
2,40
|
|
гиперболическая
|
0,9367
|
7,72
|
|
степенная
|
0,9935
|
2,40
|
|
показательная
|
0,9422
|
6,88
|
Сравнив модели по этим
характеристикам можем сделать вывод:
Степенная модель имеет большее
значение коэффициента детерминации R2
небольшую относительную ошибку
аппроксимации Еотн., следовательно, степенная модель лучше остальных
оценивает взаимосвязь.
Приложение 1 «Применение MS Excel для нахождения
параметров регрессии»
Приложение 2 «Расчет
остатков»
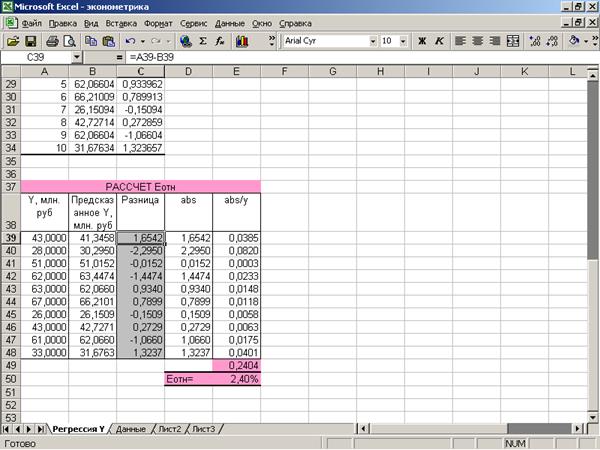
Приложение 3 «Расчет
остаточной суммы квадратов и дисперсии остатков» 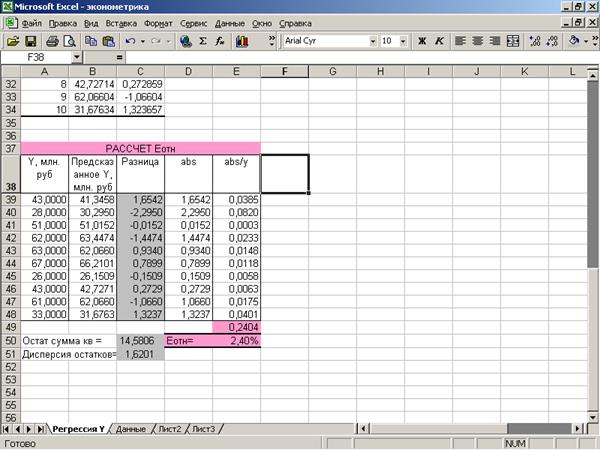
Приложение 4 «График
остатков»
Приложение 5 «Вычисление
среднего значения остатков»
Приложение 6 «Поиск
коэффициента автокорреляции»
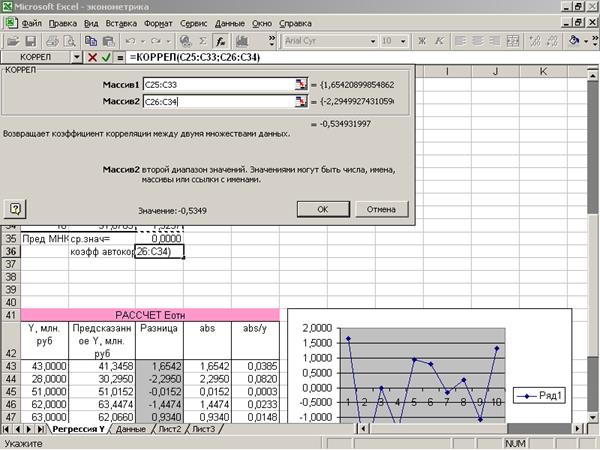
Приложение 7 «Нахождение
табличного значения t-статистики»
Приложение 8 «R/S-критерий»
Приложение 9 «Сортировка данных»
Приложение 10 «Поиск
табличного значения F-статистики»
Приложение 11 «Значения t-статистики»
Приложение 12 «Табличное
значение t-критерия»
Приложение 13 «Значение F-критерия Фишера»
Приложение 14 «Нахождение
табличного значения F-критерия»
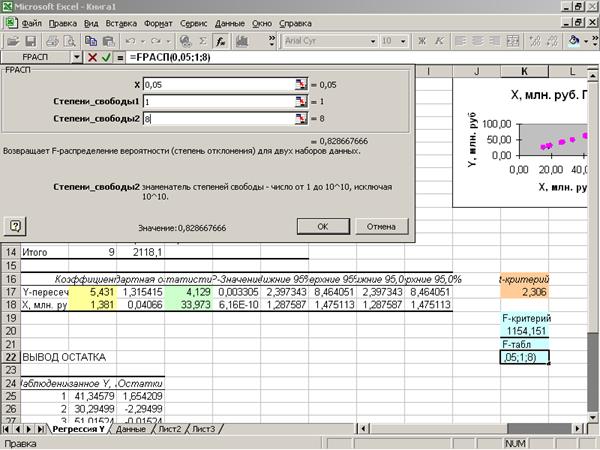
Приложение 15 «Расчет
средней относительный ошибки аппроксимации»
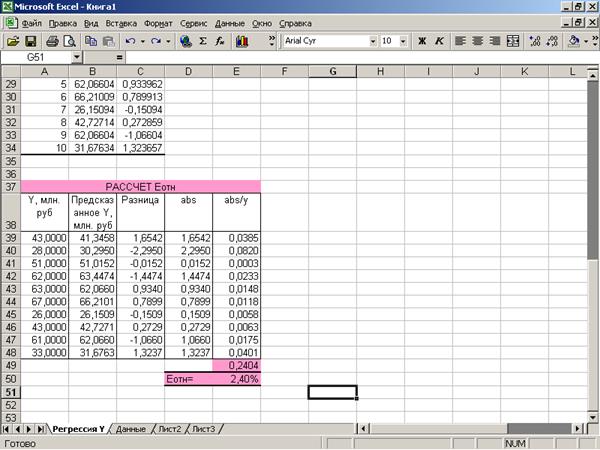
Приложение 16
«Прогнозирование среднего значения Y»
Приложение 17 «График
линейной регрессии» 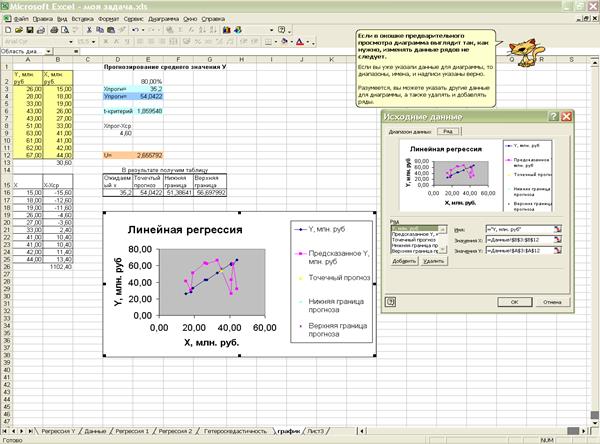
Приложение 18 «Построение
модели гиперболической регрессии и расчеты её точности»
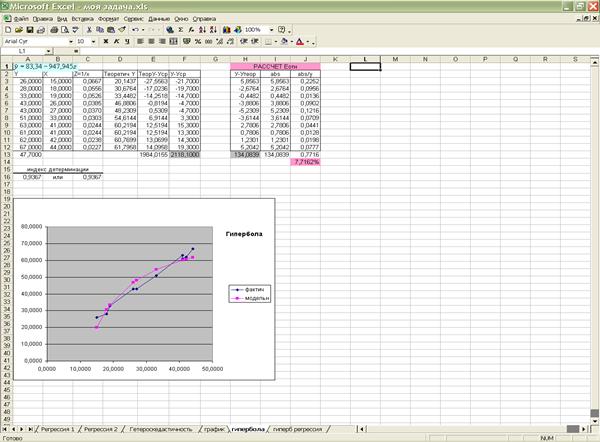
Приложение 19 «Построение
модели степенной регрессии и расчеты её точности»
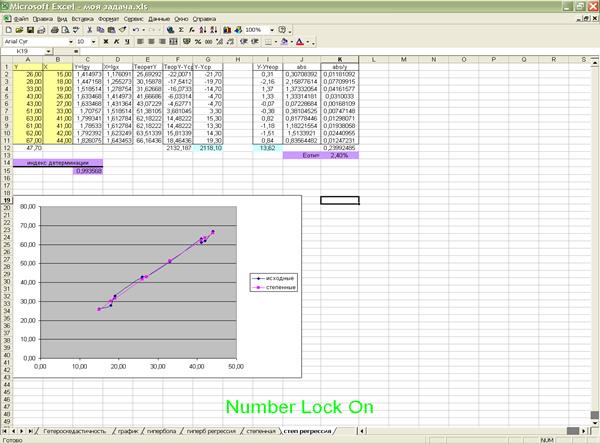
Приложение 20 «Построение
модели степенной регрессии»