ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА СТАТИСТИКИ
О Т Ч Е Т
о результатах
выполнения
компьютерной
лабораторной работы №1
«Автоматизированный
априорный анализ статистической совокупности
в среде MS Excel»
Вариант №344
Выполнил:
ст. III курса гр. день
Ф.И.О.
Проверил: Теймурова Т. Ю.
Ф.И.О.
Калуга
-2007-
1. Постановка задачи.
При
проведении статистического наблюдения за деятельностью предприятий корпорации
получены выборочные данные по 32-м предприятиям, выпускающим однородную
продукцию (выборка 10%-ная,
механическая), о среднегодовой стоимости основных производственных фондов
и о выпуске продукции за год.
В
проводимом статистическом исследовании обследованные предприятия выступают как
единицы выборочной совокупности, а показатели Среднегодовая стоимость основных производственных фондов и Выпуск продукции – как изучаемые
признаки единиц.
|
|
|
Таблица 1
|
|
|
Исходные
данные
|
|
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
1
|
18674,00
|
17819,00
|
|
2
|
21961,00
|
19549,00
|
|
3
|
22653,00
|
21798,00
|
|
4
|
23864,00
|
24220,00
|
|
5
|
15560,00
|
12110,00
|
|
6
|
25075,00
|
20760,00
|
|
7
|
25767,00
|
28026,00
|
|
8
|
19366,00
|
19030,00
|
|
9
|
23691,00
|
22317,00
|
|
10
|
27324,00
|
27853,00
|
|
12
|
10370,00
|
25950,00
|
|
11
|
29919,00
|
29410,00
|
|
13
|
22826,00
|
23182,00
|
|
14
|
25075,00
|
25258,00
|
|
15
|
28708,00
|
30621,00
|
|
16
|
32860,00
|
32870,00
|
|
17
|
24556,00
|
22144,00
|
|
18
|
27151,00
|
26296,00
|
|
19
|
21615,00
|
16435,00
|
|
20
|
27497,00
|
22490,00
|
|
21
|
30611,00
|
30275,00
|
|
22
|
21096,00
|
17127,00
|
|
23
|
16771,00
|
16089,00
|
|
24
|
28016,00
|
25777,00
|
|
25
|
25075,00
|
22490,00
|
|
26
|
23345,00
|
21279,00
|
|
27
|
18155,00
|
13840,00
|
|
28
|
24383,00
|
21625,00
|
|
29
|
28189,00
|
23701,00
|
|
31
|
32860,00
|
8650,00
|
|
30
|
26805,00
|
22490,00
|
|
32
|
19712,00
|
20068,00
|
В
процессе исследования совокупности необходимо решить ряд статистических задач
для выборочной
и генеральной совокупностей.
Статистический анализ выборочной
совокупности. Выявить наличие среди исходных данных резко
выделяющихся значений признаков («выбросов» данных) с целью исключения из
выборки аномальных единиц наблюдения.
1. Рассчитать обобщающие статистические
показатели совокупности по изучаемым признакам: среднюю арифметическую (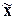 ), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию (
), моду (Мо), медиану
(Ме), размах вариации (R), дисперсию ( ), средние отклонения – линейное (
), средние отклонения – линейное (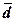 ) и квадратическое (σn), коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
) и квадратическое (σn), коэффициент вариации (Vσ),
структурный коэффициент асимметрии
К.Пирсона (Asп).
2. На основе рассчитанных показателей в
предположении, что распределения единиц по обоим признакам близки к
нормальному, оценить:
а) степень колеблемости значений
признаков в совокупности;
б)
степень однородности совокупности по изучаемым признакам;
в)
устойчивость индивидуальных значений признаков;
г) количество
попаданий индивидуальных значений признаков в диапазоны (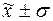 ), (
), (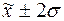 ), (
), (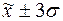 ).
).
3. Дать сравнительную характеристику
распределений единиц совокупности по двум изучаемым признакам на основе
анализа:
а)
вариации признаков;
б)
количественной однородности единиц;
в)
надежности (типичности) средних значений признаков;
г) симметричности распределений в центральной части ряда.
4.
Построить интервальный вариационный ряд и гистограмму распределения единиц
совокупности по признаку Среднегодовая
стоимость основных производственных фондов и установить характер (тип)
этого распределения. Рассчитать моду Мо полученного интервального ряда и
сравнить ее с показателем Мо несгруппированного ряда
данных.
1. Статистический анализ
генеральной совокупности. Рассчитать генеральную дисперсию  , генеральное
среднее квадратическое отклонение
, генеральное
среднее квадратическое отклонение 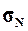 и ожидаемый размах вариации признаков RN. Сопоставить значения этих
показателей для генеральной и выборочной дисперсий.
и ожидаемый размах вариации признаков RN. Сопоставить значения этих
показателей для генеральной и выборочной дисперсий.
Для изучаемых признаков рассчитать:
а)
среднюю ошибку выборки;
б) предельные
ошибки выборки для уровней надежности P=0,683, P=0,954, P=0,997 и границы, в
которых будут находиться средние значения признака генеральной совокупности при
заданных уровнях надежности.
2. Рассчитать коэффициенты асимметрии As и эксцесса Ek. На основе
полученных оценок сделать вывод о
степени близости распределения единиц генеральной совокупности к нормальному
распределению.
2. Выполнение статистических
расчетов.
Задание1
1. Построим точечную диаграмму рассеяния изучаемых
признаков.
2. Найдем на диаграмме аномальные точки.
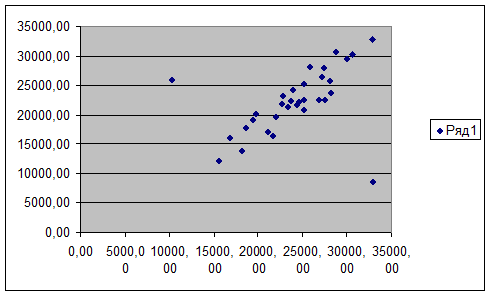
Рис.1
В нашем случаи это точки 12(10370,00; 25950,00) и 31 (32860,00; 8650,00)
|
|
|
Таблица 2
|
|
Аномальные единицы наблюдения
|
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
12
|
10370,00
|
25950,00
|
|
31
|
32860,00
|
8650,00
|
3. Удаляем эти точки из таблицы исходных
данных.
После исключения аномальных наблюдений первичные данные
принимают вид, представленный в таблице 1а.
Таблица 1а
|
|
Исходные
данные
|
|
|
Номер
предприятия
|
Среднегодовая
стоимость основных производственных фондов, млн.руб.
|
Выпуск
продукции, млн. руб.
|
|
1
|
18674,00
|
17819,00
|
|
2
|
21961,00
|
19549,00
|
|
3
|
22653,00
|
21798,00
|
|
4
|
23864,00
|
24220,00
|
|
5
|
15560,00
|
12110,00
|
|
6
|
25075,00
|
20760,00
|
|
7
|
25767,00
|
28026,00
|
|
8
|
19366,00
|
19030,00
|
|
9
|
23691,00
|
22317,00
|
|
10
|
27324,00
|
27853,00
|
|
11
|
29919,00
|
29410,00
|
|
13
|
22826,00
|
23182,00
|
|
14
|
25075,00
|
25258,00
|
|
15
|
28708,00
|
30621,00
|
|
16
|
32860,00
|
32870,00
|
|
17
|
24556,00
|
22144,00
|
|
18
|
27151,00
|
26296,00
|
|
19
|
21615,00
|
16435,00
|
|
20
|
27497,00
|
22490,00
|
|
21
|
30611,00
|
30275,00
|
|
22
|
21096,00
|
17127,00
|
|
23
|
16771,00
|
16089,00
|
|
24
|
28016,00
|
25777,00
|
|
25
|
25075,00
|
22490,00
|
|
26
|
23345,00
|
21279,00
|
|
27
|
18155,00
|
13840,00
|
|
28
|
24383,00
|
21625,00
|
|
29
|
28189,00
|
23701,00
|
|
30
|
26805,00
|
22490,00
|
|
32
|
19712,00
|
20068,00
|
Задание2
1. Произведем
расчет описательных параметров выборочной и генеральной совокупности с
использованием инструмента описательная
статистика.
Таблица 3
|
Описательные
статистики
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Среднее
|
24210
|
Среднее
|
22564,96667
|
|
Стандартная
ошибка
|
763,96983
|
Стандартная
ошибка
|
911,350407
|
|
Медиана
|
24469,5
|
Медиана
|
22403,5
|
|
Мода
|
25075
|
Мода
|
22490
|
|
Стандартное
отклонение
|
4184,435091
|
Стандартное
отклонение
|
4991,671757
|
|
Дисперсия
выборки
|
17509497,03
|
Дисперсия
выборки
|
24916786,93
|
|
Эксцесс
|
-0,344943844
|
Эксцесс
|
-0,205332365
|
|
Асимметричность
|
-0,152503649
|
Асимметричность
|
0,042954448
|
|
Интервал
|
17300
|
Интервал
|
20760
|
|
Минимум
|
15560
|
Минимум
|
12110
|
|
Максимум
|
32860
|
Максимум
|
32870
|
|
Сумма
|
726300
|
Сумма
|
676949
|
|
Счет
|
30
|
Счет
|
30
|
|
Уровень
надежности(95,4%)
|
1592,73274
|
Уровень
надежности(95,4%)
|
1899,993395
|
Чтобы определить значение
признака, характерное для всей изучаемой совокупности единиц, прибегают к
расчету средних величин. Средней
величиной в статистике называется
обобщающий
показатель, характеризующий типичный уровень явления в конкретных условиях
места и времени, отражающий величину варьирующего признака в расчете на единицу качественно однородной совокупности
Мода МО - значение случайной величины, встречающееся с
наибольшей
вероятностью, в дискретном вариационном ряду - вариант, имеющий наибольшую
частоту.
Моды
вычисляется по формуле: 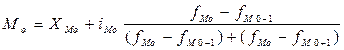
Где Хмо - нижняя граница модального интервала; i мо -
модальный интервал; fMO, fMo-1, fMo+1
- частоты в модальном, предыдущем и следующем за модальным интервалах (соответственно)
Медиана Me - это вариант, который находится в середине вариационного ряда. Медиана
делит ряд на две равные (по числу единиц) части - со значениями признака меньше медианы и со значениями признака больше
медианы. Медиана определяется по
формуле: 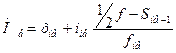
Хме - нижняя
граница медианного интервала; i ме - величина медианного интервала; f ме - частота
медианного интервала; SMe-1 - накопленная частота интервала
предшествующего медианному интервалу
2. Оценим предельные ошибки выборки для различных
уровней надежности в режиме описательная
статистика.
Для уровня надежности 68,3% при р=0,683
Таблица 4а
|
Предельные
ошибки выборки
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Уровень
надежности(68,3%)
|
777,8785028
|
Уровень
надежности(68,3%)
|
927,9422593
|
Для
уровня надежности 99,7% при р=0,997
Таблица 4б
|
Предельные
ошибки выборки
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Столбец1
|
|
Столбец2
|
|
|
|
|
|
|
|
Уровень
надежности(99,7%)
|
2474,811561
|
Уровень
надежности(99,7%)
|
2952,237686
|
Предельные ошибки выборки
∆ позволяет определить предельные значения показателей генеральной
совокупности и их доверительные интервалы. Для генеральной средней предельные
значения и доверительные интервалы определяются выражениями:
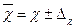
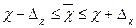
3. Произведем расчеты описательных
параметров выборочной совокупности с использованием инструмента мастера функции.
3.1
Расчет выборочного стандартного отклонения σn для признаков Среднегодовой стоимости основных
производственных фондов и выпуска продукции;
3.2Расчет
выборочной дисперсии  по признакам
Среднегодовой стоимости основных производственных фондов и Выпуска продукции;
по признакам
Среднегодовой стоимости основных производственных фондов и Выпуска продукции;
3.3
Расчет выборочного среднего линейного отклонения 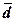 по изучаемым признакам;
по изучаемым признакам;
3.4
Расчет коэффициента вариации Vσ по изучаемым признакам;
3.5
Расчет выборочного коэффициента асимметрии Пирсона Asn по изучаемым признакам.
Таблица 5
|
|
Выборочные показатели вариации и асимметрии
|
|
|
По столбцу
"Среднегодовая стоимость основных производственных фондов,
млн.руб."
|
По столбцу
"Выпуск продукции, млн.руб"
|
|
Стандартное
отклонение
|
4114,103442
|
Стандартное
отклонение
|
4907,772139
|
|
Дисперсия
|
16925847,13
|
Дисперсия
|
24086227,37
|
|
Среднее
линейное отклонение
|
3310,066667
|
Среднее
линейное отклонение
|
3780,626667
|
|
Коэффициент
вариации, %
|
16,99340538
|
Коэффициент
вариации, %
|
21,74952089
|
|
Коэффициент
асимметрии
|
-0,21025237
|
Коэффициент
асимметрии
|
0,015275091
|
Коэффициент вариации представляет собой выраженное в процентах
отношение среднего квадратического отклонения к средней арифметической:
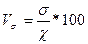 Коэффициент
вариации используют не только для сравнительной оценки вариации единиц
совокупности, но и как характеристику однородности совокупности
Коэффициент
вариации используют не только для сравнительной оценки вариации единиц
совокупности, но и как характеристику однородности совокупности
Показатели асимметрии оценивают смещение ряда распределения влево или вправо по
отношению к оси симметрии нормального распределения. 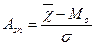
Задание3
1. Построение промежуточной таблицы.
Таблица 6
|
Карман
|
Частота
|
|
|
1
|
|
19020
|
3
|
|
22480
|
5
|
|
25940
|
11
|
|
29400
|
7
|
|
32860
|
3
|
|
|
|
2.
Генерация выходной таблицы и графиков.
3. Приведение
выходной таблицы и диаграммы к виду, принятому в статистике.
Таблица 7
|
Интервальный
ряд распределения предприятий
по стоимости основных производственных
фондов
|
|
Группа
предприятий по стоимости основных фондов
|
Число
предприятий в группе
|
Накопленная частость группы.%
|
|
15560-19020
|
4
|
13,33%
|
|
19020-22480
|
5
|
30,00%
|
|
22480-25940
|
11
|
66,67%
|
|
25940-29400
|
7
|
90,00%
|
|
29400-32860
|
3
|
100,00%
|
|
|
|
|
|
Итого
|
30
|
|
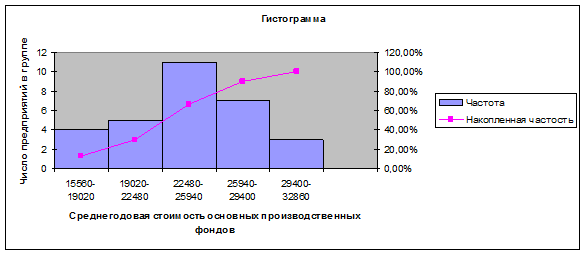
Рис.2
График – диаграмма распределение предприятий по стоимости основных
производственных фондов и выпуску продукции.
Гистограмма
– это столбиковая диаграмма, для построения которой на оси абсцисс откладывают
отрезки, равные величине интервалов вариационного ряда. На отрезках строят
прямоугольники, высота которых в принятом масштабе по оси ординат соответствует
частотам.
Заключение
В
совокупности из 32 - х предприятий наблюдается
взаимосвязь между стоимостью основных
производственных фондов и объемом выпуска продукции. Однако предприятие №
12 и предприятие № 31 резко отличаются от общих тенденций. Так, например,
предприятие № 12 имеет наименьшую стоимость основных средств и большой объем
выпуска продукции. Следовательно, оно может специализироваться на другой
отрасли, этот признак не специфичен. В предприятии № 31 наблюдается обратная
ситуация, оно имеет большую стоимость основных средств и небольшой объем
выпуска продукции. Следовательно, этот признак специфичен. Таким образом, мы
выявили наличие среди исходных данных резко выделяющиеся значения признаков с
целью исключения из выборки аномальных единиц наблюдения. Аномальные единицы
наблюдения представлены в таблице 2.
Анализ средней показывает, что среднегодовая
стоимость основных производственных фондов составляет 24210 млн. руб., а выпуск продукции 22564,96667
млн. руб.
Анализ моды показывает, что наиболее часто
встречающийся показатель среднегодовой стоимости основных производственных
фондов имеет значение 25075 млн. руб. По столбцу «Выпуск продукции» наиболее
часто встречающимся показателем является
значение 22490 млн. руб.
Анализ медианы показывает, что из 30 предприятий 15
имеют среднегодовую стоимость основных
производственных фондов более 24469,5млн. руб., а другие 15 предприятий
менее. Также значение медианы говорит о том, что из 30 предприятий 15 имеют
выпуск продукции более 22403,5 млн. руб., а другие 15 предприятий менее.
Анализ предельных ошибок выборки определяет ожидаемые границы для
средних. С вероятностью 0,683 можно утверждать, что среднегодовая стоимость
основных производственных фондов одного
предприятия по всем предприятиям отрасли будет находиться в пределах от 20026,56
до 28394,44; с вероятностью 0,954 в
пределах от 15841,12 до 32578,87; с вероятностью 0,997 от 11656,69 до 36763,31.
Также можно утверждать, что с вероятностью 0,683 средний выпуск продукции
одного предприятия по всем предприятиям отрасли будет находиться в пределах от 17573,29
до 27556,64; с вероятностью 0,954 в пределах от 12581,62 до 32548,31; с вероятностью 0,997 в пределах от 7589,95 до 37539,98.
Анализ коэффициента эксцесса (Еk) определяется следующими
показателями:
Для первого признака
коэффициент (Еk= -0,344943844) Еk<0,
следовательно вершина кривой распределения располагается выше вершины
нормальной кривой, а форма кривой является более островершинной, чем
нормальная. Это говорит о скоплении значений признака в центральной зоне ряда
распределения, т.е. о преимущественном появлении в данных значений, близких к
средним. Для второго признака (Еk= -0,205332365) Еk<0,
следовательно вершина кривой распределения лежит выше вершины нормальной
кривой, а форма кривой более островершинной по сравнению с нормальной.
Анализ коэффициентов вариации определяет, что степень колеблемости значений признаков в совокупности незначительная, поскольку полученные значения
коэффициентов вариации для двух признаков располагаются в пределах 0%<Vσ<40% т.е. для первого
признака коэффициент вариации равен 16,99379059% а для второго признака 21,74952089%. Совокупность по изучаемым
признакам является количественно однородной, так как выполняется неравенство Vσ<33%, характерное для нормальных и близких к нормальному
распределений. Поскольку значение показателя вариации для каждого признака
невелико, то индивидуальные значения признака
мало отличаются друг от друга, единицы наблюдения количественно
однородны и следовательно, средняя арифметическая величина каждого признака
является надежной характеристикой данной совокупности.
Анализ показателей асимметрии говорит о том, что поскольку 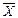 < Me < Mo и Asn1 <
0 для первого признака характерна
левосторонняя асимметрия (Asn1 = -0,152503649),
а для второго признака характерна
правостороння асимметрия, т.к. (Asn2 = 0,042954448)
< Me < Mo и Asn1 <
0 для первого признака характерна
левосторонняя асимметрия (Asn1 = -0,152503649),
а для второго признака характерна
правостороння асимметрия, т.к. (Asn2 = 0,042954448)
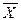 < Me < Mo и Asп2 >
0 . Так как для обоих признаков
< Me < Mo и Asп2 >
0 . Так как для обоих признаков 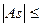 0,25, то
асимметрия незначительная.
0,25, то
асимметрия незначительная.
Рассматривая
таблицу № 7 и график можно сделать вывод, что наибольшее число предприятий 18
или 60% имеют среднегодовую стоимость основных производственных фондов от 22480
до 24975. Наименьшее число предприятий 3 или 10% имеют среднегодовую стоимость
основных производственных фондов от 24975 и выше.