1.    Теоретическая часть

1.    1 Предмет и метод статистики

Свой предмет статистика изучает методом обобщающих показателей. Она анализирует также природные ресурсы и природные условия, поскольку они влияют на жизнь общества.

Теоретической основой статистики являются положения социально-экономической теории, которые рассматривают законы развития социально-экономических явлений, выясняют их природу и значение в жизни общества. Статистика — отрасль общественной науки, изу­чающая методом обобщающих показателей количественную сто­рону качественно определенных массовых социально-экономических явлений и закономерностей их развития в конкретных условиях места и времени.

Для изучения предмета статистики разработаны и приме­няются специфические приемы, совокупность которых образует методологию статистики (методы массовых наблюдений, груп­пировок, обобщающих показателей, динамических рядов, ин­дексный метод и др.) Применение в статистике конкретных методов предопределяется поставленными задачами и зависит от характера исходной информации.

Статистика опирается на такие диалектические категории, как количество и качество, необходимость и случай­ность, причинность, закономерность, единичное и массовое, инди­видуальное и общее.

Статистические методы используются комплексно (системно). Это обусловлено сложностью процесса экономико-статисти­ческого исследования, состоящего из трех основных стадий:

первая — сбор первичной статистической информации;

вторая — статистическая сводка и обработка первичной информации;

третья   —   обобщение   и   интерпретация   статистической информации.

На третьей стадии проводится анализ статистической информации на основе применения обобщающих статис­тических показателей: абсолютных, относительных и средних величин, вариации, тесноты связи и скорости изменения соци­ально-экономических явлений во времени, индексов и др. Проведение анализа позволяет проверить причинно-следственные связи изучаемых явлений и процессов, опреде­лить влияние и взаимодействие различных факторов, оценить эффективность принимаемых управленческих решений, воз­можные экономические и социальные последствия склады­вающихся ситуаций.

При изучении статистической информации широкое применение имеют табличный и графические методы.

1.2 Выборочный метод в статистике

Статистическое наблюдение можно организовать сплош­ное и не сплошное.  Сплошное наблюдение предусматривает об­следование всех единиц изучаемой совокупности и связано с большими трудовыми и материальными затратами. Изучение не всех единиц совокупности, а лишь некоторой части, по кото­рой следует судить о свойствах всей совокупности в целом, можно осуществить не сплошным наблюдением.  В статистиче­ской практике самым распространенным является выборочное наблюдение.

Выборочное наблюдение — это такое не сплошное наблюде­ние, при котором отбор подлежащих обследованию единиц осуществляется в случайном порядке, отобранная часть изуча­ется, а результаты распространяются на всю исходную сово­купность. Наблюдение организуется таким образом, что эта:, часть отобранных единиц в уменьшенном масштабе репрезен­тирует (представляет) всю совокупность.

Выборочный метод обладает следующими достоинствами:

- относительно небольшие материальные, трудовые и стоимостные затраты на сбор данных;

- оперативность получения результатов;

- широкая область применения;

- высокая достоверность результатов.

Все эти достоинства проявляются лишь при условии правильного решения проблем выборочного обследования. К ним относится:

1.                      Определение границ генеральной совокупности;

2.                      Разработка программы наблюдения и инструкций;

3.                      Определение основы для проведения выборки – списка единицы генеральной совокупности, сведений об их размещении и т. д.;

4.                      Установление допустимого размера погрешности и определения объема выборки;

5.                      Определение вида выборочного наблюдения;

6.                      Установление сроков проведения наблюдения;

7.                      Определение потребности в кадрах для проведения выборочного наблюдения, их подготовка;

8.                      Оценка точности и достоверности данных выборки, определение порядка их распространения на генеральную совокупность.

Совокупность, из которой производится отбор, называется генеральной, и все ее обобщающие показатели — генеральными.

Совокупность отобранных единиц именуют выборочной сово­купностью, и все ее обобщающие показатели — выборочными.

Основная задача выборочного наблюдения в экономике состоит в том, чтобы на основе характеристик выборочной со­вокупности (средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности. При этом следует иметь в виду, что при любых статистических ис­следованиях (сплошных и выборочных) возникают ошибки двух видов: регистрации и репрезентативности.

Ошибки регистрации могут иметь случайный (непредна­меренный) и систематический (тенденциозный) характер. Слу­чайные ошибки обычно уравновешивают друг друга, поскольку не имеют преимущественного направления в сторону преуве­личения или преуменьшения значения изучаемого показателя. Систематические ошибки направлены в одну сторону вследст­вие преднамеренного нарушения правил отбора (предвзятые цели). Их можно избежать при правильной организации и проведении наблюдения.

Ошибки репрезентативности присущи только выбороч­ному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную. Они представляют собой расхождение между значениями показателей, полученных по выборке, и значениями показателей этих же величин, которые были бы получены при про­веденном с одинаковой степенью точности сплошном на­блюдении, т.е. между величинами выборных и соответст­вующих генеральных показателей.

Для каждого конкретного выборочного наблюдения зна­чение ошибки репрезентативности может быть определено по соответствующим формулам, которые зависят от вида, метода и способа формирования выборочной совокупности.

По виду различают индивидуальный, групповой и комби­нированный отбор. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной со­вокупности; при групповом отборе — качественно однородные группы или серии изучаемых единиц; комбинированный отбор предполагает сочетание первого и второго видов.

По методу отбора различают повторную и бесповторную выборки.

При повторной выборке общая численность единиц гене­ральной совокупности в процессе выборки остается неизмен­ной. Ту или иную единицу, попавшую в выборку, после регист­рации снова возвращают в генеральную совокупность, и она сохраняет равную возможность со всеми прочими единицами при повторном отборе единиц вновь попасть в выборку ("отбор по схеме возвращенного шара"). Повторная выборка в соци­ально-экономической жизни встречается редко. Обычно вы­борку организуют по схеме бесповторной выборки.

При бесповторной выборке единица совокупности, попав­шая в выборку, в генеральную совокупность не возвращается и в дальнейшем в выборке не участвует; т.е. последующую вы­борку делают из генеральной совокупности уже без отобранных ранее единиц ("отбор по схеме невозвращенного шара"). Таким образом, при бесповторной выборке численность единиц гене­ральной совокупности сокращается в процессе исследования.

Способом отбора определяется конкретный механизм или процедура выборки единиц из генеральной совокупности.

По степени охвата единиц совокупности различают боль­шие и малые (n<30) выборки.

В практике выборочных исследований наибольшее рас­пространение получили следующие виды выборки: собственно -случайная, механическая, типическая, серийная, комбинированная.

Основные характеристики параметров генеральной и выборочной совокупностей обозначаются символами:

N – объем генеральной совокупности (число входящих в нее единиц);

n – объем выборки (число обследованных единиц);

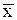 – генеральная средняя (среднее значение признака в генеральной совокупности);

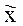– выборочная средняя;

P – генеральная   доля    (доля    единиц,    обладающих данным   значением   признака   в   общем   числе единиц генеральной совокупности);

w – выборочная доля;

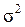– генеральная дисперсия (дисперсия признака в ге­неральной совокупности);

S2 – выборочная дисперсия того же признака;

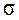– среднее квадратическое отклонение в генеральной в совокупности;

S – среднее квадратическое отклонение в выборке.

Ошибки выборки

При выборочном наблюдении должна быть обеспечена случайность отбора единиц. Каждая единица должна иметь рав­ную с другими возможность быть отобранной. Именно на этом основывается собственно-случайная выборка.

К собственно-случайной выборке относится отбор еди­ниц из всей генеральной совокупности (без предваритель­ного расчленения ее на какие-либо группы) посредством жеребьевки (преимущественно) или какого-либо иного по­добного способа, например, с помощью таблицы случайных чисел. Случайный отбор — это отбор не беспорядочный. Принцип случайности предполагает, что на включение или исключение объекта из выборки не может повлиять какой-либо фактор, кроме случая.

Определение способа отбора и процедуры выборки, вычисление ошибок выборки и построение доверительных интервалов выборочных характеристик, расчет необходимого объема выборки.

Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности. Различают среднюю и предельную ошибки выборки.

Эти два вида ошибок связаны следующим соотношением:

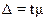,                                    (1.1)

где Δ – предельная ошибка;

t – коэффициент доверия, определяемый в зависимости от уровня вероятности;

µ - средняя ошибка выборки.

Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки. Так, при случайном повторном отборе средняя ошибка определяется по формуле при повторной выборки:

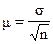,                                   (1.2)

При бесповторном:

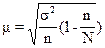,                                  (1.3)

где 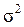- выборочная (или генеральная) дисперсия;

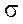- выборочная (или генеральная) среднее квадратное отклонение;

n – объем выборочной совокупности;

N – объем генеральной совокупности.

Расчет средней и предельной ошибки выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности. Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:

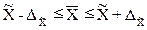,                                   (1.4)

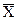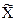где и- генеральная и выборочная средние соответственно;

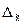- предельная ошибка выборочной средней.

Пример:

В городе проживают 250 тыс. семей. Для определения среднего числа детей в семье было организована 2%-ная, случайная, бесповторная выборка семей. По ее результату было получено следующее распределение семей по числу детей (таблица 1):

Таблица 1.1

Распределение семей по числу детей

Число детей в семье

0

1

2

3

4

5

Количество семей

1000

2000

1200

400

200

200

 С вероятностью 0,954 найдите пределы, в которых будут находиться среднее число детей в генеральной совокупности?

Решение:

Вначале на основе имеющегося распределения семей определим выборочную среднюю и дисперсию:

;

.

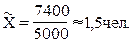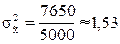Число детей в семье, хi

Количество семей, fi

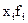
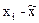
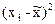
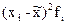
0

1

2

3

4

5

1000

2000

1200

400

200

200

0

2000

2400

1200

800

1000

-1,5

-0,5

0,5

1,5

2,5

3,5

2,25

0,25

0,25

2,25

6,25

12,25

2250

500

300

900

1250

2450

Итого

5000

7400

-

-

7650

Вычислим предельную ошибку выборки (с учетом того, что ).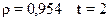

Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака. В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется по формуле:

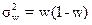,                                     (1.5)

где 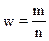 - доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.

Тогда, например, при собственно-случайном повторном отборе для определения предельной ошибки выборки используется формула:

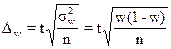,                     (1.6)

Соответственно при бесповторном отборе:

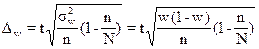,             (1.7)

Пределы доли признака в генеральной совокупности 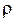выглядят следующим образом:

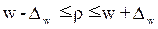.                        (1.8)

Ошибки и пределы генеральных характеристик при других способах формирования выборочной совокупности определяются на основе соответствующих формул, отражающих особенности этих видов выборки. Например, в случае типической выборки показателем вариации является средняя из внутригрупповых дисперсий 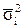, при серийной выборке – межгрупповая дисперсия  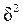и т. д. Кроме, того в последнем случае вместо объема выборочной совокупности  n используется показатель числа серий  r.

Следовательно, для типической выборки средняя ошибка вычисляется по формуле:

- при отборе, пропорциональном объему типических групп:

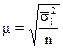 (повторный отбор);                    (1.9)

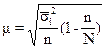 (бесповторный отбор).                (1.10)

- при отборе, пропорциональном вариации признака (не пропорциональных объем групп):

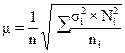(повторный отбор);                  (1.11)

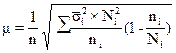(бесповторный отбор),            (1.12)

где Ni и ni – объем i-ой типической группы и выборки из нее соответственно;

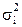- групповые дисперсии.

При серийной выборки средняя ошибка определяется следующим образом:

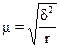 (повторный отбор);                    (1.13)

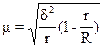 (бесповторный отбор),                (1.14)

где R – число серий в генеральной совокупности;

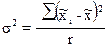 - межгрупповая (межсерийная) дисперсия;    (1.15)

r – число серий в выборочной совокупности.

Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки.

Приведем наиболее часто применяемые на практике выражения необходимого объема выборки:

- собственно – случайная и механическая выборка:

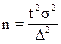 (повторный отбор);                    (1.16)

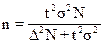 (бесповторный отбор).                           (1.17)

- типическая выборка:

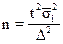 (повторный отбор);                    (1.18)

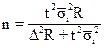 (бесповторный отбор).                           (1.19)

- серийная выборка:

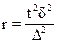 (повторный отбор);                     (1.20)

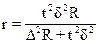 (бесповторный отбор).       (1.21)

При этом в зависимости от целей исследования дисперсии и ошибки выборки могут быть рассчитаны для средней величины или доли признака.

 

2.    Расчетная часть

ТЕМА: Выборочный метод изучения производственных и финансовых показателей.

Имеются следующие выборочные данные по предприятиям одной из отраслей промышленности региона в отчетном году (выборка 20%-ная механическая), млн.руб. (таблица 1.1):

№ предприятия п/п

Выручка от продажи продукции

Затраты на производство и реализацию продукции

№ предприятия п/п

Выручка от продажи продукции

Затраты на производство и реализацию продукции

1

36,45

30,255

16

36,936

31,026

2

23,4

20,124

17

53,392

42,714

3

46,540

38,163

18

41,0

33,62

4

59,752

47,204

19

55,680

43,987

5

41,415

33,546

20

18,2

15,652

6

26,86

22,831

21

31,8

26,394

7

79,2

60,984

22

39,204

32,539

8

54,720

43,776

23

57,128

45,702

9

40,424

33,148

24

28,44

23,89

10

30,21

25,376

25

43,344

35,542

11

42,418

34,359

26

70,720

54,454

12

64,575

51,014

27

41,832

34,302

13

51,612

41,806

28

69,345

54,089

14

35,42

29,753

29

35,903

30,159

15

14,4

12,528

30

50,220

40,678

Таблица 2.1

Исходные данные

Задание 1

Исследование структуры совокупности по исходным данным:

1.    Построить статистический ряд распределения организации по признаку уровня рентабельности продукции, образовав заданное число групп (по условию пять) с равными интервалами.

2.    Построить графики полученного ряда распределения. Графически определить моду и медиану.

3.    Рассчитать характеристики интервального ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации.

4.    Вычислить среднюю арифметическую по исходным данным, для интервального ряда распределения. Объяснить причину расхождения.

Сделать выводы по результатам выполнения задания.

Решение: Уровень рентабельности рассчитывается путем деления прибыли от продаж, т.е. разности между выручкой от продаж продукции и затратами на ее производство и реализацию, на затраты на производство и реализацию продукции.

Пусть:

Уровень рентабельности продукции – Z;

Прибыль от продаж – К;

Выручка от продаж продукции – Х;

Затраты на производство и реализацию продукции – У.

Следовательно: прибыль от продаж рассчитывается по формуле (2.1):

К = Х – У                                        (2.1)

уровень рентабельности продукции рассчитаем по формуле (2.2):

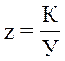.                                          (2.2)

Расчеты для построения статистического ряда распределения организации представлены в таблице 2.2.

Таблица 2.2

Расчеты для построения статистического ряда распределения организации по уровню рентабельности

№ предприятия

Выручка от продажи, С

Затраты на производство и реализацию продукции, В

Прибыль от продаж, Р

Уровень рентабельности продукции, U

1

36,45

30,255

6,195

0,20476

2

23,4

20,124

3,276

0,16279

3

46,540

38,163

8,377

0,21951

4

59,752

47,204

12,548

0,26582

5

41,415

33,546

7,869

0,23457

6

26,86

22,831

4,029

0,17647

7

79,2

60,984

18,216

0,29870

8

54,720

43,776

10,944

0,25000

9

40,424

33,148

7,276

0,21950

10

30,21

25,376

4,834

0,19049

11

42,418

34,359

8,059

0,23455

12

64,575

51,014

13,561

0,26583

13

51,612

41,806

9,806

0,23456

14

35,42

29,753

5,667

0,19047

15

14,4

12,528

1,872

0,14943

16

36,936

31,026

5,91

0,19049

17

53,392

42,714

10,678

0,24999

18

41,0

33,62

7,38

0,21951

19

55,680

43,987

11,693

0,26583

20

18,2

15,652

2,548

0,16279

21

31,8

26,394

5,406

0,20482

22

39,204

32,539

6,665

0,20483

23

57,128

45,702

11,426

0,25001

24

28,44

23,89

4,55

0,19046

25

43,344

35,542

7,802

0,21951

26

70,720

54,454

16,266

0,29871

27

41,832

34,302

7,53

0,21952

28

69,345

54,089

15,256

0,28205

29

35,903

30,159

5,744

0,19046

30

50,220

40,678

9,542

0,23457

1. Построение интервального ряда распределения организаций по уровню рентабельности продукции

Для построения интервального вариационного ряда, характеризующего распределение организаций по уровню рентабельности, необходимо вычислить величину и границы интервалов ряда.

При построении ряда с равными интервалами величина интервала h определяется по формуле (2.3):

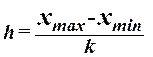,                         (2.3)

где 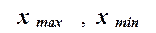 – наибольшее и наименьшее значения признака в исследуемой совокупности,  k- число групп интервального ряда.

Число групп k задается в условии задания или рассчитывается по формуле Г. Стерджесса

k=1+3,322lg n,                                    (2.4)

где  n - число единиц совокупности.

Определение величины интервала по формуле (2.3) при заданных k = 5,           xmax = 0,29871 млн руб., xmin = 0,14943 млн руб.:

 

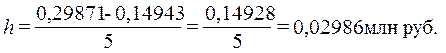
При h = 0,02986 млн. руб. границы интервалов ряда распределения имеют следующий вид (табл. 2.3):

Таблица 2.3

Нижние и верхние границы группы

Номер группы

Нижняя граница,

Верхняя граница,

млн руб.

млн руб.

1

0,14943

0,17928

2

0,17928

0,20914

3

0,20914

0,23900

4

0,23900

0,26885

5

0,26885

0,29871

Для построения интервального ряда необходимо подсчитать число предприятий, входящих в каждую группу (частоты групп). При этом возникает вопрос, в какую группу включать единицы совокупности, у которых значения признака выступают одновременно и верхней, и нижней границами смежных интервалов (для демонстрационного примера – это 0,17928; 0,20914; 0,23900; 0,26885 млн. руб.). Отнесение таких единиц к одной из двух смежных групп рекомендуется осуществлять по принципу полуоткрытого интервала. Т.к. при этом верхние границы интервалов не принадлежат данным интервалам, то соответствующие им единицы совокупности включаются не в данную группу, а в следующую. В последний интервал включаются и нижняя, и верхняя границы.

Процесс группировки единиц совокупности по признаку уровня рентабельности продукции представлен во вспомогательной (разработочной) таблице 2.4 (графы 3, 4 этой таблицы необходима для построения аналитической группировки в Задании 2).

Таблица 2.4

Разработочная таблица для построения интервального ряда распределения и аналитической группировки

№ группы

№ предприятия

Затраты на производство и реализацию продукции

Уровень рентабельности продукции

1

2

3

4

0,14943 - 0,17928

2

20,124

0,16279

6

22,831

0,17647

15

12,528

0,14943

20

15,652

0,16279

Всего

4

71,135

0,65148

0,17928 - 0,20914

1

30,255

0,20476

10

25,376

0,19049

14

29,753

0,19047

16

31,026

0,19049

21

26,394

0,20482

22

32,539

0,20483

24

23,89

0,19046

29

30,159

0,19046

Всего

8

229,392

1,56677

1

2

3

4

0,20914 - 0,23900

3

33,148

0,21950

5

33,62

0,21951

9

33,546

0,23457

11

34,302

0,21952

13

34,359

0,23455

18

35,542

0,21951

25

38,163

0,21951

27

40,678

0,23457

30

41,806

0,23456

Всего

9

325,164

2,03581

0,23900 - 0,26885

4

42,714

0,24999

8

43,776

0,25000

12

43,987

0,26583

17

45,702

0,25001

19

47,204

0,26582

23

51,014

0,26583

Всего

6

274,397

1,54748

0,26885 - 0,29871

7

54,089

0,28205

26

54,454

0,29871

28

60,984

0,29870

Всего

3

169,527

0,87947

ИТОГО

22

1069,62

6,68101

На основе групповых итоговых строк «Всего» табл. 2.4 формируется итоговая таблица 2.5, представляющая интервальный ряд распределения организаций по уровню рентабельности продукции.

Таблица 2.5

Распределение организаций по уровню рентабельности продукции

Номер группы

Группы организаций по рентабельности продукции,  млн руб., х

Число предприятий,

f

1

0,14943 – 0,17928

4

2

0,17928 – 0,20914

8

3

0,20914 – 0,23900

9

4

0,23900 – 0,26885

6

5

0,26885 – 0,29871

3

Итого

30

Помимо частот групп в абсолютном выражении в анализе интервальных рядов используются ещё четыре характеристики ряда, приведенные в графе 5 табл. 2.6. Это частоты групп в относительном выражении, накопленные (кумулятивные) частоты Sj, получаемые путем последовательного суммирования частот всех предшествующих (j-1) интервалов, и накопленные частости, рассчитываемые по формуле 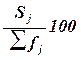(2.5):

                                        (2.5)

Таблица 2.6

Структура организаций по уровню рентабельности продукции

№ группы

Группы организаций по уровню рентабельности продукции, млн. руб.

Число организаций, fj

Накопленная

частота,

Sj

Накопленная

частоcть, %

в абсолютном выражении

в % к итогу

1

2

3

4

5

6

1

0,14943 – 0,17928

4

13,333

4

13,333

2

0,17928 – 0,20914

8

26,667

12

40,0

3

0,20914 – 0,23900

9

30,0

21

70,0

4

0,23900 – 0,26885

6

20,0

27

90,0

5

0,26885 – 0,29871

3

10,0

30

100,0

Итого

30

100,0

Вывод. Анализ интервального ряда распределения изучаемой совокупности организаций показывает, что распределение организаций по уровню рентабельности продукций не является равномерным: преобладают организации с уровнем рентабельности от 0,20914 млн. руб. до 0,23900 млн. руб. (это 9 предприятий, доля которых составляет 30%); 26,7% организаций имеют уровень рентабельности менее 0,20914 млн. руб., а 20% – более 0,23900 млн. руб.

2. Нахождение моды и медианы полученного интервального ряда распределения графическим методом и  путем расчетов

Мода и медиана являются структурными средними величинами, характеризующими (наряду со средней арифметической) центр распределения единиц совокупности по изучаемому признаку.

Мода Мо для дискретного ряда – это значение признака, наиболее часто встречающееся у единиц исследуемой совокупности[1]. В интервальном вариационном ряду модой приближенно считается центральное значение модального интервала (имеющего наибольшую частоту). Более точно моду можно определить графическим методом по гистограмме ряда (рис.1).

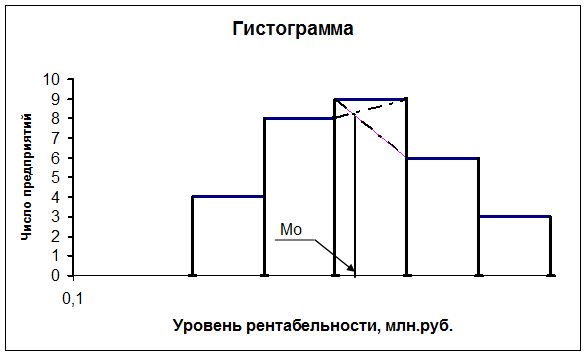
Рис. 1 Определение моды графическим методом

Конкретное значение моды для интервального ряда рассчитывается по формуле 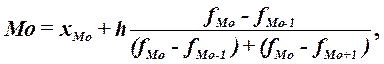(2.6):

      (2.6)

где   хМo – нижняя граница модального интервала,

h –величина модального интервала,

fMo – частота модального интервала,

fMo-1 – частота интервала, предшествующего модальному,

fMo+1 – частота интервала, следующего за модальным.

Согласно табл.4 модальным интервалом построенного ряда является интервал 0,20914– 0,23900 млн. руб., так как его частота максимальна (f3 = 9).

Расчет моды по формуле (2.6):

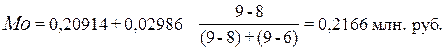
Вывод. Для рассматриваемой совокупности организации наиболее распространенная уровень рентабельности продукции характеризуется средней величиной 0,2166 млн. руб.

Медиана Ме – это значение признака, приходящееся на середину ранжированного ряда. По обе стороны от медианы находится одинаковое количество единиц совокупности.

Медиану можно определить графическим методом по кумулятивной кривой (рис. 2). Кумулята строится по накопленным частотам (табл. 2.6, графа 5).

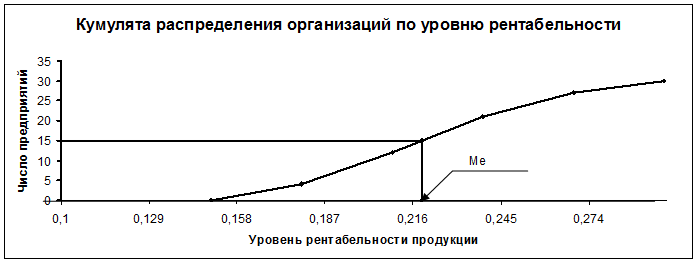
Рис. 2. Определение медианы графическим методом

Конкретное значение медианы для интервального ряда рассчитывается по формуле 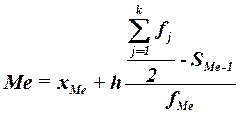(2.7):

,                           (2.7)

где    хМе– нижняя граница медианного интервала,

h – величина медианного интервала,

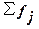– сумма всех частот,

fМе – частота медианного интервала,

SMе-1 – кумулятивная (накопленная) частота интервала, предшествующего медианному.

Для расчета медианы необходимо, прежде всего, определить медианный интервал, для чего используются накопленные частоты (или частости) из табл. 2.5 (графа 5). Так как медиана делит численность ряда пополам, она будет располагаться в том интервале, где накопленная частота впервые равна полусумме всех частот 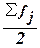 или превышает ее  (т.е. все предшествующие накопленные частоты меньше этой величины).

В демонстрационном примере медианным интервалом является интервал    0,23900 – 0,26885 млн. руб., так как именно в этом интервале накопленная частота Sj = 27 впервые превышает величину, равную половине численности единиц совокупности (=).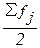

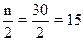Расчет значения медианы по формуле (2.7):

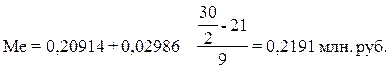
Вывод. В рассматриваемой совокупности организаций половина предприятий имеют в среднем уровень рентабельности продукции не более 0,2191 млн. руб., а другая половина – не менее 0,2191 млн. руб.

3. Расчет характеристик ряда распределения

Для расчета характеристик ряда распределения 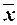, σ, σ2, Vσ на основе табл. 2.6 строится вспомогательная таблица 2.7 (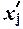 – середина j-го интервала).

Таблица 2.7

Расчетная таблица для нахождения характеристик ряда распределения

Группы организаций по выручке от продаж, млн. руб.

Число предприятий

Середина интервала   

Расчетные значения

 

f

Хср

Хср^2

Хср*f

Хср-Хар

(Хср- Хар)^2

(Хср^2)*f

((Хср- Хар)^2)*f

0,14943 – 0,17928

4

0,16435

0,02701

0,65740

-0,05574

0,00311

0,10804

0,01243

0,17928 – 0,20914

8

0,19421

0,03772

1,55368

0,19421

0,03772

0,30174

0,30174

0,20914 – 0,23900

9

0,22407

0,05021

2,01663

0,22407

0,05021

0,45187

0,45187

0,23900 – 0,26885

6

0,25393

0,06448

1,52358

0,25393

0,06448

0,38688

0,38688

0,26885 – 0,29871

3

0,28378

0,08053

0,85134

0,28378

0,08053

0,24159

0,24159

ИТОГО Σ

30

1,12034

0,25995

6,60263

0,90025

0,23604

1,49013

1,39451

Расчет средней арифметической взвешенной:

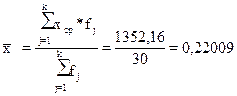                       (2.8)

Расчет среднего квадратического отклонения:

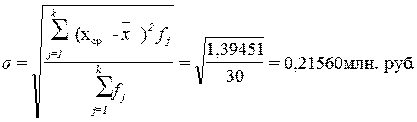   (2.9)

Расчет дисперсии:

σ2 =0,215602 = 0,04648

Расчет коэффициента вариации:

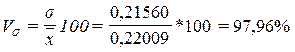                                                        (2.10)

Вывод. Анализ полученных значений показателей 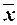                                                                                            и σ говорит о том, что средний уровень рентабельности продукции по предприятиям составляет 0,22009 млн. руб., отклонение от среднего объема в ту или иную сторону составляет в среднем 154,127 млн. руб. (или 97,96%).

Значение Vσ = 97,96% на много превышает 33%, следовательно, вариация уровня рентабельности продукции в исследуемой совокупности организаций значительна и совокупность по данному признаку качественно неоднородна. Расхождение между значениями 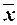, Мо и Ме значительны (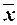=0,22009 млн. руб., Мо=0,2166 млн. руб., Ме=0,2191 млн. руб.), что подтверждает вывод об неоднородности совокупности организаций. Таким образом, найденное среднее значение уровня рентабельности продукции (0,22009 млн. руб.) является нетипичной, ненадежной характеристикой исследуемой совокупности организаций.

4.Вычисление средней арифметической по исходным данным

Для расчета применяется формула средней арифметической простой:

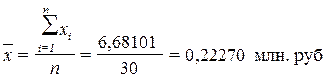                (2.11)

Причина расхождения средних величин, рассчитанных по формулам (2.11) и (2.8), заключается в том, что по формуле (2.11) средняя определяется по фактическим  значениям  исследуемого  признака  для  всех  30-ти предприятий, а по формуле (2.8) средняя вычисляется для интервального ряда, когда в качестве значений признака берутся середины интервалов хср и, следовательно, значение средней будет менее точным (за исключением случая равномерного распределения значений признака внутри каждой группы).

Задание 2

По исходным данным табл. 2.1 с использованием результатов выполнения Задания 1 необходимо выполнить следующее:

3.     Установить наличие и характер корреляционной связи между признаками Затраты на производство и  реализацию продукции и Уровень рентабельности продукции, образовав по каждому признаку пять групп с равными интервалами, используя методы:

а) аналитической группировки;

б) корреляционной таблицы.

Выполнение Задания 2

Целью выполнения данного Задания является выявление наличия корреляционной связи между факторным и результативным признаками, установление направления связи и оценка ее тесноты.

Факторный и результативный признаки либо задаются в условии задания, либо определяются путем проведения предварительного теоретического анализа. Лишь после того, как выяснена экономическая сущность явления и определены факторный и результативный признаки, приступают к проведению корреляционного анализа данных.

По условию Задания 2 факторным является признак Затраты на производство и  реализацию продукции (X), результативным – признак Уровень рентабельности продукции (Y).

 

 

 

 

1. Установление наличия и характера связи между знаками, методами аналитической группировки и корреляционной таблицы

1а. Применение метода аналитической группировки

При использовании метода аналитической группировки строится интервальный ряд распределения единиц совокупности по факторному признаку Х и для каждой j-ой группы ряда определяется среднегрупповое значение 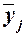 результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения 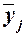 систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.

Используя разработочную таблицу 3, строим аналитическую группировку, характеризующую зависимость между факторным признаком Х – Уровень рентабельности продукции и результативным признаком Y – Затраты на производство и  реализацию продукции.

Групповые средние значения 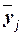 получаем из таблицы 2.4 (графа 3), основываясь на итоговых строках «Всего». Построенную аналитическую группировку представляет табл. 2.8.

Таблица 2.8

Зависимость уровня рентабельности продукции от затрат на производство и реализацию продукции, млн. руб.

Номер группы

Группы организаций по уровню рентабельности продукции,

Число предприятий

Затраты на производство и реализацию продукции, млн. руб.

всего

в среднем на одно предприятие

1

2

3

4

5=4:3

1

0,14943 – 0,17928

4

71,135

17,78375

2

0,17928 – 0,20914

8

229,392

28,674

3

0,20914 – 0,23900

9

325,164

36,12933

4

0,23900 – 0,26885

6

274,397

45,73283

5

0,26885 – 0,29871

3

169,527

56,509

 

Итого

30

1069,615

184,82892

Вывод. Анализ данных табл. 2.8 показывает, что с увеличением затрат на производство и реализацию продукции от группы к группе систематически возрастает и уровень рентабельности производства по каждой группеорганизаций, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками.

1б. Применение метода корреляционной таблицы.

Корреляционная таблица представляет собой комбинацию двух рядов распределения. Строки таблицы соответствуют группировке единиц совокупности по факторному признаку Х, а графы – группировке единиц по результативному признаку Y. На пересечении j-ой строки и k-ой графы указывается число единиц совокупности, входящих в j-ый интервал по факторному признаку и в k-ый интервал по результативному признаку. Концентрация частот около диагонали построенной таблицы свидетельствует о наличии корреляционной связи между признаками. Связь прямая, если частоты располагаются по диагонали, идущей от левого верхнего угла к правому нижнему. Расположение частот по диагонали от правого верхнего угла к левому нижнему говорит об обратной связи.

Для построения корреляционной таблицы необходимо знать величины и границы интервалов по двум признакам X и Y. Величина интервала и границы интервалов  для  факторного  признака  Х – уровень рентабельности известны из табл. 8. Для результативного признака Y – Затраты на производство и реализацию продукции величина интервала определяется по формуле (2.3) при

k = 5, 

 уmax =  60,984 млн руб., уmin = 12,528 млн руб.:

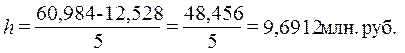
Границы интервалов ряда распределения результативного признака Y имеют следующий вид (табл. 2.9):

Таблица 2.9

Нижние и верхние границы группы

Номер группы

Нижняя граница,

млн руб.

Верхняя граница,

млн руб.

1

12,528

22,2192

2

22,2192

31,9104

3

31,9104

41,6016

4

41,6016

51,2928

5

51,2928

60,9840

Подсчитывая с использованием принципа полуоткрытого интервала: число предприятий, входящих в каждую группу (частоты групп), получаем интервальный ряд распределения результативного признака (табл. 2.10).

Таблица 2.10

Распределение предприятий по затратам на производство

и реализацию продукции

Группы организаций по уровню рентабельности продукции, млн. руб.

Число предприятий

0,14943 – 0,17928

4

0,17928 – 0,20914

8

0,20914 – 0,23900

9

0,23900 – 0,26885

6

0,26885 – 0,29871

3

Итого

30

Используя группировки по факторному и результативному признакам, строим корреляционную таблицу (табл. 2.11).

Таблица 2.11

Корреляционная таблица зависимости уровня рентабельности и затратами на производство и реализацию продукции

Группы организаций по уровню рентабельности продукции, млн. руб.

Группы организаций по затратам на производство и реализацию продукции, млн. руб.

 

 

12,528 - 22,219

22,219 - 31,910

31,910 - 41,602

41,602 - 51,293

51,293 - 60,984

Итого

0,14943 – 0,17928

4

 

 

 

 

4

0,17928 – 0,20914

 

8

 

 

 

8

0,20914 – 0,23900

 

 

9

 

 

9

0,23900 – 0,26885

 

 

 

6

 

6

0,26885 – 0,29871

 

 

 

 

3

3

Итого

4

8

9

6

3

30

Вывод. Анализ данных табл. 2.11 показывает, что распределение частот групп произошло вдоль диагонали, идущей из левого верхнего угла в правый нижний угол таблицы. Это свидетельствует о наличии прямой корреляционной связи между затратами на производство и реализацию продукции и уровнем рентабельности.

Задание 3

По результатам выполнения Задания 1 с вероятностью 0,997 необходимо определить:

1. Ошибку выборки среднего уровня рентабельности организации и границы, в которых будет находиться средний уровень рентабельности в генеральной совокупности;

2. Ошибку выборки доли организации с уровнем рентабельности продукции 23,9% и более и границы, в которых будет находиться генеральная доля.

Выполнение Задания 3

Целью выполнения данного Задания является определение для генеральной совокупности организаций региона границ, в которых будут находиться величина среднего уровня рентабельности продукции и доля организаций  с уровнем рентабельности продукции 23,9%.

1. Определение ошибки выборки среднего уровня рентабельности организации и границы, в которых будет находиться средний уровень рентабельности в генеральной совокупности

Применение выборочного метода наблюдения всегда связано с установлением степени достоверности оценок показателей генеральной совокупности, полученных на основе значений показателей выборочной совокупности. Достоверность этих оценок зависит от репрезентативности выборки, т.е. от того, насколько полно и адекватно  представлены в выборке статистические свойства  генеральной совокупности. Как правило, генеральные и выборочные характеристики не совпадают, а отклоняются на некоторую величину ε, которую называют ошибкой выборки (ошибкой репрезентативности).

Значения признаков единиц, отобранных из генеральной совокупности в выборочную, всегда случайны, поэтому и статистические характеристики выборки случайны, следовательно, и ошибки выборки также случайны. Ввиду этого принято вычислять два вида ошибок - среднюю 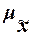 и предельную .

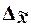Средняя ошибка выборки 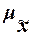 - это среднее квадратическое отклонение всех возможных значений выборочной средней от генеральной средней, т.е. от своего математического ожидания M[].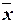

Величина средней ошибки выборки рассчитывается дифференцированно (по различным формулам) в зависимости от вида и способа отбора единиц из генеральной совокупности в выборочную.

Для собственно-случайной и механической выборки с бесповторным способом отбора средняя ошибка 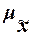 выборочной средней  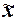определяется по формуле (1.3)

 Предельная ошибка выборки 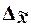 определяет границы, в пределах которых будет находиться генеральная средняя (формула 1.4):

Границы задают доверительный интервал генеральной средней, т.е. случайную область значений, которая с вероятностью Р гарантированно содержит значение генеральной средней. Эту вероятность Р называют доверительной вероятностью или уровнем надёжности.

В экономических исследованиях чаще всего используются доверительные вероятности Р= 0,954; Р= 0,997; реже  Р= 0,683.

В математической статистике доказано, что предельная ошибка выборки Δ кратна средней ошибке µ с коэффициентом кратности t (называемым также коэффициентом доверия), который зависит от значения доверительной вероятности Р. Для предельной ошибки выборочной средней 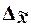 это теоретическое положение выражается формулой ():

                          (1.6)

Значения t вычислены заранее для различных доверительных вероятностей Р и протабулированы (таблицы функции Лапласа Ф). Для наиболее часто используемых уровней надежности Р значения t задаются следующим образом (табл. 3.1):

Таблица 3.1

Доверительная вероятность P

0,683

0,866

0,954

0,988

0,997

0,999

Значение t

1,0

1,5

2,0

2,5

3,0

3,5

По условию демонстрационного примера выборочная совокупность насчитывает 30 организаций, выборка 20% механическая, следовательно, генеральная совокупность включает 150 организаций. Выборочная средняя 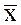, дисперсия  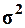определены в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи, представлены в табл. 3.2:

Таблица 3.2

Р

t

n

N

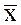
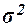
0,997

3

30

150

0,22009

0,04648

Расчет средней ошибки выборки по формуле (1.3):

,

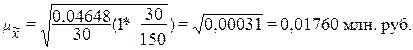Расчет предельной ошибки выборки по формуле (1.6):

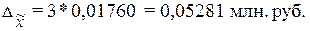
Определение по формуле (1.4) доверительного интервала для генеральной средней:

0,22009-0,05281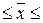0,22009+0,05281,

 0,16728 млн. руб. 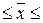0,27290 млн. руб.

Вывод. На основании проведенного выборочного исследования организаций с вероятностью 0,997 можно утверждать, что для генеральной совокупности организаций среднего уровня рентабельности продукции находится в пределах от 0,16728 млн. руб.  до 0,27290 млн. руб.

2. Ошибку выборки доли организации с уровнем рентабельности продукции 23,9% и более и границы, в которых будет находиться генеральная доля.

Доля единиц выборочной совокупности, обладающих тем или иным заданным свойством, выражается формулой 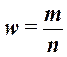(3.1):

              ,                            (3.1)

где  m – число единиц совокупности, обладающих заданным свойством;

        n – общее число единиц в совокупности.

Для собственно-случайной и механической выборки с бесповторным способом отбора предельная ошибка выборки 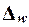 доли единиц, обладающих заданным свойством, рассчитывается по формуле (1.7)                

Предельная ошибка выборки 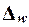 определяет границы, в пределах которых будет находиться генеральная доля р единиц, обладающих заданным свойством:

                     (3.2)

По условию Задания 3 исследуемым свойством является равенство или превышение уровня рентабельности продукции величины 0,27290 млн. руб.

Число организаций с заданным свойством определяется из табл. 2.4 (графа 3):                                                         m=3

Расчет выборочной доли по формуле (3.1):

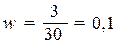
Расчет по формуле (1.7) предельной ошибки выборки для доли:

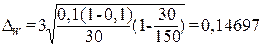
Определение по формуле (3.2) доверительного интервала генеральной доли:

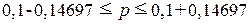
- 0,04697 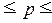 0,24697

или

- 4,697% 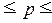 24,697%

Вывод. С вероятностью 0,997 можно утверждать, что в генеральной совокупности организаций  доля организаций с уровнем рентабельности продукции 23,9% и выше будет находиться в пределах от – 4,697% до 24,697%.

Задание 4

Использование индексного метода в финансово-экономической задачи.

Выпуск продукции и удельный расход стали по региону, в текущем периоде характеризуется следующими данными (таблица 4.1):

Таблица 4.1

Выпуск продукции и удельный расход стали по региону, в текущем периоде

Вид продукции

Фактический выпуск продукции, шт.

Расход стали на ед. продукции, кг

по норме

фактически

А

320

36

38

Б

250

15

12

В

400

10

9

Определить:

1.     Индивидуальные индексы выполнения норм расхода стали.

2.     Общий индекс выполнения норм расхода стали на весь выпуск продукции.

3.     Абсолютную экономию (перерасход) стали.

Выполнение Задания 4

1. Определим индивидуальный индекса выполнения норм расхода стали по формуле (4.1):

ip=p1/p2                         (4.1)

В этом случае получаем таблицу 4.2:

Таблица 4.2

Определение индивидуального индекса выполнения норм расхода стали

Вид продукции

Фактический выпуск продукции, шт

Расход стали на ед. продукции, кг

Индивидуальные индексы выполнения норм расхода стали

по норме

фактически

q

p0

p1

i = p1/p0

А

320

36

38

1,056

Б

250

15

12

0,8

В

400

10

9

0,9

СУММА

970

61

59

2,756

Вывод: Из определение индивидуального индекса выполнения норм расхода стали видно, что для выпуска продукции А было расходовано больше на 5,6% чем по норме, для выпуска продукции Б стали было расходовано меньше, чем должно быть по норме на 20%  и для продукции В также меньше на 10%.

2. Для определения общего индекса нужно найти расход стали на фактический выпуск продукции по каждой продукции таблица 4.3:

Таблица 4.3

Определение общего индекса выполнения норм расхода стали на весь выпуск продукции

Вид продукции

Фактический выпуск продукции, шт.

Расход стали на ед. продукции, кг

Индивидуальные индексы выполнения норм расхода стали

Расход стали на фактический выпуск продукции, шт.

по норме

фактически

по норме

фактически

q

p0

p1

i = p1/p0

p0 * q

p1 * q

А

320

36

38

1,056

11520

12160

Б

250

15

12

0,8

3750

3000

В

400

10

9

0,9

4000

3600

СУММА

970

61

59

2,756

19270

57230

Общий индекс выполнения норм расхода стали на весь выпуск продукции рассчитаем по формуле (4.2):

                                                           Iq= ∑p1q/∑p0q                 (4.2)

Следовательно получаем:  Iq=57230/19270=2,97

Вывод: Расход стали фактически по региону в текущем периоде возрос на 197%.

3.    Абсолютную экономию (перерасход) стали.

Абсолютная экономия продукции Б - 20% и продукции В - 10%, а продукция А – 5,6% перерасход стали.