3
1) Найти неопределённый интеграл:
х²dx
∫ √x³+1
.
Решение:
Пусть х³+1
= t; dt = d(x³+1) = (x³+1)'dx = 2x²dx; x²dx = ½dt
х²dx dt t־ + 1
6 √t
∫ √x³ + 1
= ½ ∫ *
√t
= ½ * -1/6 + 1 = 10 +
c = 3/5 √t
произведём
обратную замену, в результате получим: 3/5 * √(x³ + 1) + c
х²dx
Ответ: ∫
√x³+1 = 3/5 * √(х³ + 1) + с.
2) Найти определённые
интегралы:
ln 3 e dx
∫ e² - 1 .
ln 2
Решение:
Воспользуемся заменой переменной:
4
dt
Пусть e = t x = ln t и dx = t
;
Найдём пределы интегрирования:
если x = ln 2, то t = 2;
если x = ln 3, то t = 3.
Получим:
3 t dt 3 (t
– 1) + 1 * dt
3 1
3 dt
∫ t² - 1
= ∫ (t – 1) *
(t + 1) = ∫ t + 1 + ∫ t² - 1 ;
2 2
2 2
3 3
t – 1
arctg √t
+½ ln t + 1 = arctg √3
– arctg √2 + ½ (ln
½ - ln 1/3 ) =
2 2
= arctg √3 -
arctg√2 + ½ (-0,69 – 1,1) =
arctg √3 – arctg
√2 – 0,9 =
0,03 – 0,02 –
- 0,9 ≈ - 0,89
Ответ:
ln 3 e dx
∫ e²
- 1 ≈ - 0,89.
ln 2
e ln x * dx
3) ∫ √x .
1
5
Решение:
e
∫ = ln x * xˉ dx;
1
Произведём замену:
xˉ dx = dv (1)
lnx = u; du = 1/x * dx; из (1) v;
v = ∫
dv = ∫
xˉ dx = 5/4 x
;
Применяя формулу интегрирования по
частям получим:
e e e e ln x * dx e
∫ udv = uv | - ∫ vdu ∫ √x = ln x *
5/4 √x | -
1 1 1 1 1
e
e
- 5/4 ∫ √x * 1/х * dx = 5/4 * (ln ℮ * √℮ - ln 1 * √1 )
– 5/4 * 5/4 x
| =
1
1
= 5/4 * ( √℮ - 5/4 * ( √℮ - 1) ) = 5/4 * (2,23 – 5/4 * (2,23 – 1) )
≈ 0,87.
6
Ответ:
e ln x * dx
∫ √x
≈ 0,87.
1
4) Решить дифференциальное уравнение:
xdy – ydx = √y²
- 9x²dx.
Решение:
Делим обе части на dx:
y
xy' – y = dx - 9x² /x
y
y
y'
- x
- xdx =
-9x (1)
Пусть y = uv, т.е. y' = uv' + u'v, тогда уравнение (1) примет вид:
u'v + uv'
– uv * (1/x + 1/xdx) = -9x (2)
Преобразуем:
u'v + u * (v' – v * (1/x + 1/xdx)) = -9x (3)
Положим:
dv
v' – v * (1/x + 1/xdx) = 0 или dx = v * (1/x + 1/xdx);
dv
v = dx * 1/x + 1/x;
7
Интегрируем:
dv dx
∫ v = ∫ x + ∫
1/x * dx = ln |x| + ln |x|;
dt
Пусть x = t, тогда dt = d(x)' = 1 1/x =
t и
dt
∫ t = ln |t| ∫
1/x = ln |x| или ln |v| = ln x²;
Найдём какое-либо решение полученного
уравнения, например, при С = 0
ln |v| = ln x²
или v = x²
du -9x
при v = x² b(3) x² * u' = -9x dx
= x²
= -9/x;
du = -9/x * dx;
dx
∫du = -9 ∫ x
;
u = -9 ln |x| + C;
y = uv = (-9 ln |x| + C) * x² = -9 ln |x| * x² + x²C;
y = x² ln xˉ + x²C = x² ln |1/x | + x²C.
Ответ: y = x² ln |1/x | + x²C.
5) Вычислить площадь фигуры,
ограниченной линиями:
y = 3 + 2x - x², y = x + 1, х = 0.
8
Решение:
Координаты вершины параболы:
-2
x0 = - B/2a = 2*(-1) = 1;
4AC - B²
4 * (-1) * 3 - 4
y0 = 4A
= 4 * (-1) = 4;
Строим графики заданных функций.
Координаты точек для y = x + 1
9
2 2 2 2 2 2 2
SABC = ∫ (3 + 2x - x²)dx - ∫ (x – 1)dx = 2x | + ½ x²
| = 2x | + ½ x² | - 1/3 x³ | =
-1
-1
-1 -1 -1 -1 -1
= 2
* (-1 – 2 ) + ½ *
(1 – 4) – 1/3 * (1 – 8) = 31/6 ≈ 5,12.
Ответ: SABC = 5,12.
6) Опытные данные о значениях
переменных х и у приведены в таблице:
|
xi
|
7
|
8
|
9
|
10
|
11
|
|
yi
|
2,5
|
2,2
|
2,0
|
1,8
|
1,7
|
В результате их выравнивания
дробнолинейной функцией получено
х + 3
уравнение у = х – 3 . Используя метод
наименьших квадратов, аппроксимировать эти данные линейной зависимостью у = ax + b (найти параметры a и b). Установить, какая из двух линий
лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные
данные. Сделать чертёж.
10
Решение:
|
хi
|
yi
|
xi yi
|
x²i
|
|
7
|
2,5
|
17,5
|
49
|
|
8
|
2,2
|
17,6
|
64
|
|
9
|
2
|
18
|
81
|
|
10
|
1,8
|
18
|
100
|
|
11
|
1,7
|
18,7
|
121
|
|
∑ 45
|
10,2
|
89.8
|
415
|
5 5 5
∑ (x²i)a + ∑ (xi)b = ∑ xi yi ;
i=1 i=1 i=1
5 5
∑ (xi)a + 5b = ∑ yi;
i=1 i=1
415a
+ 45b = 89,8
10,2 – 5b
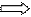45a + 5b = 10,2 a = 45 ;
415 * (10,2 – 5b)
+ 45b = 89,8;
45
11
4233 – 2075b + 2025b = 4041;
- 50b = - 192;
b = 3,84;
10,2 – 5 * 3,84
a = 45 = -0,2.
y = - 0,2x + 3,84
12
х + 3
Для функции y = - 0,2х + 3.84: Для функции у = х – 3
:
если х = 7, то у = 2,44; если х
= 7, то у = 2,5;
если х = 8, то у = 2,24; если х
= 8, то у = 2,2;
если х = 9, то у = 2,04; если х = 9,
то у = 2;
если х = 10, то у = 1,84; если х =
10, то у = 1,86;
если х = 11, то у = 1,64. если х =
11, то у = 1,75.
∑ δ¹i =
2,5 – 2,44 + 2,24 – 2,2 + 2,04 – 2 + 1,84 – 1,8 + 1,7 – 1,64 = 0,24;
(у= -0,2х+3,84)
∑ δ²i = 2,5 – 2,5 + 2,2 – 2,2 + 2 – 2 + 1,86 – 1,8 + 1,75 –
1,7 = 0,11;
х+3
(у= х-3 )
х + 3
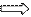∑δ¹i
= 0,24 › ∑δ²i
= 0,11 функция у = х – 3
лучше выравнивает
экспериментальные данные.
х + 3
Ответ: функция у = х – 3
лучше выравнивает экспериментальные данные.
7) Исследовать на абсолютную и условную сходимость
ряд:
n
∞ (-1) * (n + 1)
∑ n
n=1 2
* (n – 1) .
Решение:
Предел общего члена ряда:
13
(-1) (n + 1) (-1) 2
lim un = lim 2 * (n
– 1) = lim 2 (1 + n
+ 1) = 0, так как
n→∞
n→∞
(-1)
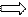lim 2 = 0
по признаку Лейбница ряд сходится, так как члены
n→∞
ряда убывают. Ряд, составленный из абсолютных величин членов
данного ряда
n
∞ (-1) * (n + 1)
∑ n
n=1 2 * (n –
1) , убывает.
2 + 1
3 + 1 5 n + 1
2² * (2 – 1)
› 2³
* (3 – 1) › 2 * 4 › …. 2 (n - 1) ›….
n + 1
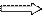0,75 › 0,25 › 0,078 › …. 2 (n – 1)
›…. ряд сходится.
Ответ: ряд абсолютно
сходящийся.
14
Список
литературы.
Основная
1) Высшая математика для экономистов.
/ Под редакцией Н.Ш. Кремера, М.: Банки и биржи, 1998, 2000, 2001, 2002.
2) Практикум по высшей математике для
экономистов. / Под редакцией Н.Ш. Кремера, М.: ЮНИТИ (в печати).
Дополнительная
3) Карасев А.И., Аксютина З.М.,
Савельева Т.И. Курс высшей математики для экономических вузов, ч.1, М.: Высшая
школа, 1982.
4) Карасев А.И., Калихман И.Л.,
Кремер Н.Ш. Матричная алгебра, М.: ВЗФЭИ, 1987.
5) Руководство к решению задач с
экономическим содержанием по курсу высшей математики. / Под редакцией А.И. Карасева,
Н.Ш. Кремера, М.: ВЗФЭИ, 1989.
6) Кудрявцев В.А., Демидович В.П.
Краткий курс высшей математики, М.: Наука, 1985.
Содержание.
Задание №1………………………………………………………………….3
Задание №2………………………………………………………………….3
Задание №3………………………………………………………………….4
Задание №4………………………………………………………………….6
Задание №5………………………………………………………………….7
Задание №6………………………………………………………………….9
Задание №7…………………………………………………………………12
Список
литературы………………………………………………………...14