Всероссийский заочный  Финансово-Экономический институт

Кафедра математики и информатики

Отчет по аудиторной работе

 Вариант 26

По дисциплине «эконометрика»

 

г. Барнаул 2006

Задание 26

В табл. представлены данные о рынке строящегося жилья в Санкт-Петербурге.

№п/п	Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	У
1	3	1	74,7	46,3	10,7	0	1	12	28,7
2	3	1	71,7	45,9	10,7	0	0	0	27,2
3	3	1	74,5	47,5	10,4	0	0	0	28,3
4	4	1	137,7	87,2	14,6	0	1	0	52,3
5	1	1	40	17,7	11	1	1	8	22
6	2	1	53	31,1	10	1	1	8	28
7	3	1	86	48,7	14	1	1	8	45
8	4	1	98	65,8	13	1	1	8	51
9	2	1	62,6	21,4	11	1	1	0	34,4
10	1	1	45,3	20,6	10,4	1	1	8	24,7
11	2	1	56,4	29,7	9,4	1	1	8	30,8
12	1	1	37	17,8	8,3	0	1	0	15,9
13	3	1	67,5	43,5	8,3	0	1	0	29
14	1	1	37	17,8	8,3	0	1	3	15,4
15	3	1	69	42,4	8,3	0	1	3	28,6
16	1	1	40	20	8,3	0	0	0	15,6
17	3	1	69,1	41,3	8,3	0	1	0	27,7
18	2	1	68,1	35,4	13	1	1	20	34,1
19	2	1	75,3	41,4	12,1	1	1	20	37,7
20	3	1	83,7	48,5	12,1	1	1	20	41,9

Принятые в таблице обозначения:

У – цена квартиры, тыс. долл.;

Х₁ – число комнат в квартире;

Х₂ – район города ( 1 – Приморский, Шувалово – Озерки, 2 – Гражданка, 3 – Юго-запад, 4 – Красносельский);

Х₃ – общая площадь квартиры (м²);

Х₄ – жилая площадь квартиры (м²)

Х₅ – площадь кухни (м²);

Х₆ – тип дома ( 1 – кирпичный, 0 – другой);

Х₇ – наличие балкона ( 1 – есть, 0 – нет);

Х₈ – число месяцев до окончания срока строительства.

Задание

1. введите фиктивную переменную z, отражающую местоположение квартиры и позволяющую разделить всю совокупность квартир на две группы : квартиры на севере города ( приморский район, Шувалово – Озерки, Гражданка) и на юге города ( Юго-запад, Красносельский район).

2. Составьте матрицу парных коэффициентов корреляции исходных переменных. Вместо переменной х² используйте фиктивную переменную z.

3. Постройте уравнение регрессии, характеризующее зависимость цены от всех факторов, в линейной форме. Установите, какие факторы мультиколлинеарны.

4. Постройте модель  у= f (х_3,х₆, х₇, х₈, z) в линейной форме. Какие факторы значимо воздействуют на формирование цены квартиры в этой модели?

5. Существует ли разница в ценах квартир, расположенных в северной и южной частях Санкт-Петербурга?

6. Оцените статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о значимости уравнения проверьте с помощью F-критерия; оцените качество уравнения регрессии с помощью коэффициента детерминации R².

Решение:

1.      Построение системы показателей (факторов). Анализ матрицы коэффициентов парной корреляции. Выбор факторных признаков для построения двухфакторной регрессионной модели

Таблица

№п/п	Х1	Х3	Х4	Х5	Х6	Х7	Х8	У	Z
1	3	74,7	46,3	10,7	0	1	12	28,7	1
2	3	71,7	45,9	10,7	0	0	0	27,2	1
3	3	74,5	47,5	10,4	0	0	0	28,3	1
4	4	137,7	87,2	14,6	0	1	0	52,3	1
5	1	40	17,7	11	1	1	8	22	1
6	2	53	31,1	10	1	1	8	28	1
7	3	86	48,7	14	1	1	8	45	1
8	4	98	65,8	13	1	1	8	51	1
9	2	62,6	21,4	11	1	1	0	34,4	1
10	1	45,3	20,6	10,4	1	1	8	24,7	1
11	2	56,4	29,7	9,4	1	1	8	30,8	1
12	1	37	17,8	8,3	0	1	0	15,9	1
13	3	67,5	43,5	8,3	0	1	0	29	1
14	1	37	17,8	8,3	0	1	3	15,4	1
15	3	69	42,4	8,3	0	1	3	28,6	1
16	1	40	20	8,3	0	0	0	15,6	1
17	3	69,1	41,3	8,3	0	1	0	27,7	1
18	2	68,1	35,4	13	1	1	20	34,1	1
19	2	75,3	41,4	12,1	1	1	20	37,7	1
20	3	83,7	48,5	12,1	1	1	20	41,9	1

Статистические данные по всем  переменным приведены в таблице. Количество наблюдений n=20, а число факторных переменных m=7.

Для проведения корреляционного анализа выполняем:

1. Данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек.
2. Выберите команду Сервис →Анализ данных.
3. В диалоговом окне Анализ данных выберите инструмент Корреляция, затем щелкните на кнопке ОК.
4. В диалоговом окне Корреляция в поле Входной интервал необходимо ввести диапазон ячеек, содержащих исходные данные. 
5. Выберите параметры ввода.
6. ОК

Результат корреляционного анализа:

Таблица 1.1

	У	Х1	Х3	Х4	Х5	Х6	Х7	Х8	Z 2
У	1
Х1	0,7714	1
Х3	0,8979	0,8841	1
Х4	0,8248	0,9224	0,9706	1
Х5	0,8370	0,4596	0,7233	0,6191	1
Х6	0,3929	-0,1558	-0,0210	-0,1431	0,5028	1
Х7	0,2944	0,0073	0,0948	0,0170	0,1728	0,4201	1
Х8	0,3287	-0,0308	0,0940	0,0420	0,4701	0,6522	0,3836	1
Z 2	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	1

Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная цена квартиры, имеет тесную связь с числом комнат в квартире (r_ух1= 0,7714), с общей площадью квартиры ( r_ух3=0,8979), с жилой площадью квартиры (r_ух4=0,8248) и с площадью кухни (r_ух5=0,8370).

Проверим выполнение условий для каждой  пары факторных переменных:

Коэффициент корреляции между двумя факторными переменными должен быть меньше 0,8 и одновременно меньше коэффициентов корреляции между исследуемой переменной и каждой из этих факторов.

Если хотя бы одно из условий неравенств не выполняется, то в модель включают только один из этих двух факторов, а именно тот, у которого модуль коэффициента корреляции с у больше. 

│rxіxј│<0,8

│rxіxј│<│ryxі│

│rxіxј│<│ryxј│

Х1Х3

0,8841 <0,8  (не выполняется)

0,8841 <0,7714   (не выполняется)

0,8841 <0,8979  (выполняется)

Х1Х4

0,9224 <0,8   (не выполняется)

0,9224 <0,7714 (не выполняется)

0,9224 <0,8248  (не выполняется)

Х3Х4

0,9706 <0,8  (не выполняется)

0,9706 <0,8979  (не выполняется)

0,9706 <0,8248   (не выполняется)

Факторы Х1 и Х3 мультиколлинеарны, их не рекомендуется использовать в модели одновременно, т.к. коэффициент парной корреляции больше 0,8, r_x1x3 =0,8841.

Факторы Х1 и Х4 мультиколлинеарны, их не рекомендуется использовать в модели одновременно, т.к. коэффициент парной корреляции больше 0,8, r_х1х4=0,9224.

Факторы Х3 и Х4 мультиколлинеарны, их не рекомендуется использовать в модели одновременно, т.к. r_х3х4=0,9706>0,8.

Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, цена квартиры,  имеет тесную связь с числом комнат в квартире (rух₁=0,7714), с общей площадью квартиры (ryx3=0,8979), с жилой площадью квартиры (ryx4=0,8248) и с площадью кухни (ryx5=0,8370).Факторы Х3 и Х4 тесно связаны между собой (rx3x4=0,9706), что свидетельствует о наличии мультиколлинеарности. Из этих двух переменных оставим в модели Х3,т.к.эта переменная теснее связана с зависимой переменной У.

       Для проведения регрессионного анализа выполняем:

1.Выберите команду Сервис →Анализ данных.

2.В диалоговом окне Анализ данных выберите инструмент Регрессия, затем щелкните на кнопке ОК.

3. В диалоговом окне Регрессия в поле Входной интервал У введите адрес одного диапазона ячеек, который представляет зависимую переменную. В поле Входной интервал Х введите адреса одного или нескольких диапазонов, которые содержат значения независимых переменных.

4. если выделены и заголовки столбцов, то установить флажок Метки в первой строке.

5. выберите параметры вывода.

6. в поле Остатки поставьте необходимые флажки.

7. ОК

Таблица 1.2

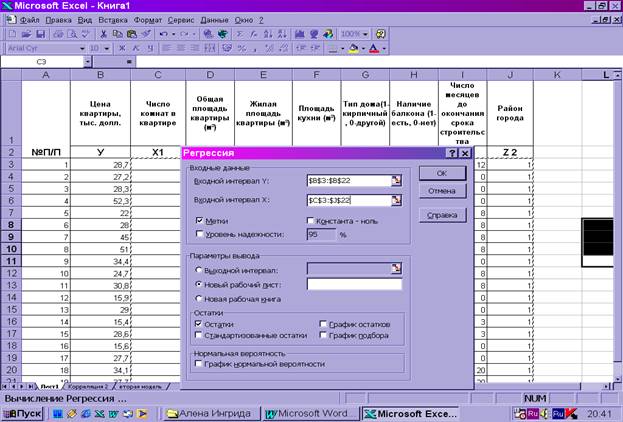
 Таблица 1.3

Регрессионная статистика
Множественный R	0,992352488
R-квадрат	0,98476346
Нормированный R-квадрат	0,975875479
Стандартная ошибка	1,64080082
Наблюдения	20

Таблица 1.4

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	7	2088,0388	298,2913	110,7972	6,036E-10
Остаток	12	32,306728	2,692227
Итого	19	2120,3455

Таблица 1.5

	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	-1,939	3,575	-0,542
Х1	2,050	1,174	1,746
Х3	0,345	0,096	3,578
Х4	-0,034	0,126	-0,266
Х5	0,073	0,533	0,137
Х6	8,863	1,466	6,043
Х7	1,546	1,270	1,218
Х8	-0,066	0,077	-0,852

Y=-1,939+2,050*Х1+0,345*Х3-0,034*Х4+0,073*Х5+8,863*Х6+1,546*Х7-0,066*Х8

Таблица 1.6

Наблюдение	Предсказанное У	Остатки	У
1	29,959	-1,259	28,7	-0,0439	0,0439
2	28,183	-0,983	27,2	-0,0362	0,0362
3	29,074	-0,774	28,3	-0,0273	0,0273
4	53,444	-1,144	52,3	-0,0219	0,0219
5	23,998	-1,998	22	-0,0908	0,0908
6	30,009	-2,009	28	-0,0718	0,0718
7	43,144	1,856	45	0,0413	0,0413
8	48,686	2,314	51	0,0454	0,0454
9	34,247	0,153	34,4	0,0045	0,0045
10	25,685	-0,985	24,7	-0,0399	0,0399
11	31,185	-0,385	30,8	-0,0125	0,0125
12	14,428	1,472	15,9	0,0926	0,0926
13	28,186	0,814	29	0,0281	0,0281
14	14,230	1,170	15,4	0,0760	0,0760
15	28,542	0,058	28,6	0,0020	0,0020
16	13,843	1,757	15,6	0,1126	0,1126
17	28,811	-1,111	27,7	-0,0401	0,0401
18	34,501	-0,401	34,1	-0,0118	0,0118
19	36,718	0,982	37,7	0,0261	0,0261
20	41,427	0,473	41,9	0,0113	0,0113
			сумма		0,8358
					4,1791

Относительная ошибка апроксимации   Еотн =4,1791. 4,1791<15%, следовательно модель имеет высокую точность.

2. Оценка качества всего уравнения регрессии

В табл.1.5 приведены вычисления по модели значения зависимой переменной У и значения остаточной компоненты .

Значение коэффициентов детерминации и множественной корреляции можно найти в таблице1.2.

Оценим качество уравнения регрессии с помощью коэффициента детерминации R²=0,985, следовательно, около 98% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.

Коэффициент множественной корреляции R: R==0,992.

Он показывает тесноту связи зависимой переменной У с двумя включенными в модель объясняющими факторами.

3. Проверка значимости уравнения регрессии. с помощью F- критерия Фишера.

Табличное значение F- критерия  при доверительной вероятности 0,05 при v₁= к=7 и v₂=20-7-1=12 составляет 2,913. Табличное значение F- критерия можно найти с помощью функции FРАСПОБР

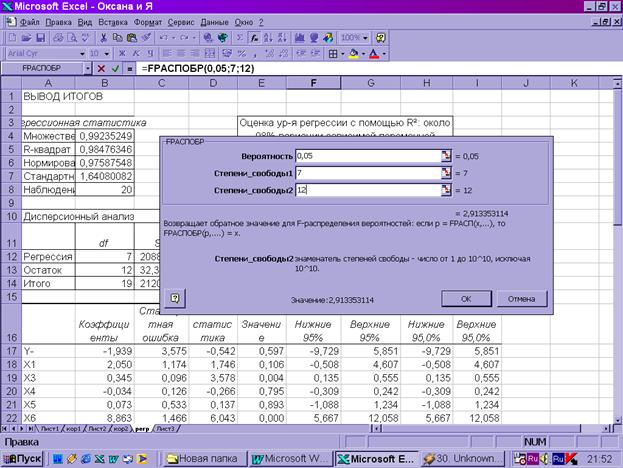
Поскольку Fрасч>Fтабл (110,797>2,913),   уравнение регрессии следует признать адекватным.

4. Оценить с помощью критерия t-критерия Стьюдента статистическую значимость коэффициентов уравнения регрессии

Оценим статистическую значимость параметров регрессионной модели у=f(x₁;х₃;х₄;х₅;х₆;х₇;х₈) с помощью t-критерия Стьюдента.

Табличное значение t –критерия Стьюдента найдем с помощью функции СТЬЮДРАСПОБР.

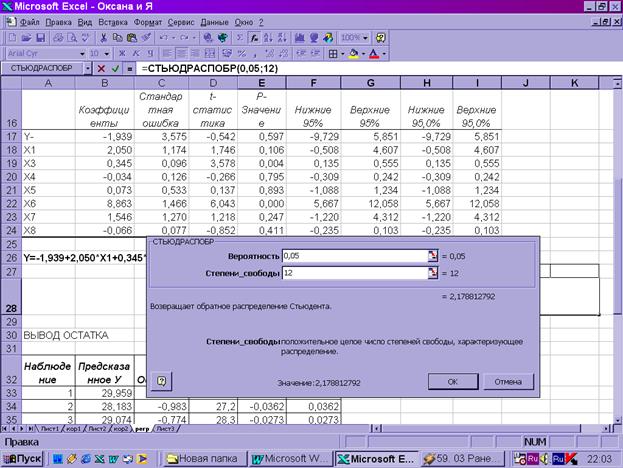
	t-расчетное	t-табличное
ta0	-0,5424	2,1788
ta1	1,7459	2,1788
ta3	3,5781	2,1788
ta4	-0,2655	2,1788
ta5	0,1371	2,1788
ta6	6,0434	2,1788
ta7	1,2175	2,1788
ta8	-0,8522	2,1788

Табличное значение t- критерия при 5%- уровне значимости и степенях свободы (20-7-1=12) составляет 2,179. Так как  t_рас>t_табл, то коэффициенты а₃ и а₆ существенны (значимы)

5. Построим модель y=f(x₃,x_6,x_7,x₈,z).

Цена квартиры, тыс. долл.	Общая площадь квартиры (м²)	Тип дома(1-кирпичный, 0-другой)	Наличие балкона (1-есть, 0-нет)	Число месяцев до окончания срока строительства	Район города
У	Х3	Х6	Х7	Х8	Z 2
28,7	74,7	0	1	12	1
27,2	71,7	0	0	0	1
28,3	74,5	0	0	0	1
52,3	137,7	0	1	0	1
22	40	1	1	8	1
28	53	1	1	8	1
45	86	1	1	8	1
51	98	1	1	8	1
34,4	62,6	1	1	0	1
24,7	45,3	1	1	8	1
30,8	56,4	1	1	8	1
15,9	37	0	1	0	1
29	67,5	0	1	0	1
15,4	37	0	1	3	1
28,6	69	0	1	3	1
15,6	40	0	0	0	1
27,7	69,1	0	1	0	1
34,1	68,1	1	1	20	1
37,7	75,3	1	1	20	1
41,9	83,7	1	1	20	1

У=-1,1657+0,4006*Х3+8,7667*Х6+1,4404*Х7-0,0796*Х8

Находим матрицу парных коэффициентов корреляции модели y=f(x₃,x_6,x_7,x₈,z) с помощью MS Excel аналогично первому примеру (Сервис→Анализ данных →Корреля- ция).

Результат корреляционного анализа:

Таблица 2.1

	У	Х3	Х6	Х7	Х8	Z 2
У	1
Х3	0,897883	1
Х6	0,392853	-0,02102	1
Х7	0,294364	0,09484	0,420084	1
Х8	0,328739	0,094	0,652174	0,383555	1
Z 2	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	1

На формирование цены квартиры  воздействуют общая площадь квартиры Х3 rху3=0,8979.

Таблица 2.2

Регрессионная статистика
Множественный R	0,989389217
R-квадрат	0,978891022
Нормированный R-квадрат	0,973261962
Стандартная ошибка	1,727393527
Наблюдения	20

Таблица 2.3

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	4	2075,58717	518,8968	173,8995	2,263E-12
Остаток	15	44,7583259	2,983888
Итого	19	2120,3455

Таблица 2.4

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
Y-пересечение	-1,1657	1,4436	-0,8075	0,4320	-4,2426	1,9112	-4,2426	1,9112
Х3	0,4006	0,0168	23,8246	0,0000	0,3648	0,4365	0,3648	0,4365
Х6	8,7667	1,0593	8,2761	0,0000	6,5089	11,0245	6,5089	11,0245
Х7	1,4404	1,2128	1,1877	0,2534	-1,1446	4,0254	-1,1446	4,0254
х8	-0,0796	0,0754	-1,0553	0,3080	-0,2403	0,0811	-0,2403	0,0811

У=-1,1657+0,4006*Х3+8,7667*Х6+1,4404*Х7-0,0796*Х8

Наблюдение	Предсказанное У	Остатки	У	Еi/Yi	|Еi/Yi|
1	29,247	-0,547	28,7	-0,019	0,019
2	27,559	-0,359	27,2	-0,013	0,013
3	28,681	-0,381	28,3	-0,013	0,013
4	55,441	-3,141	52,3	-0,060	0,060
5	24,430	-2,430	22	-0,110	0,110
6	29,638	-1,638	28	-0,059	0,059
7	42,859	2,141	45	0,048	0,048
8	47,666	3,334	51	0,065	0,065
9	34,121	0,279	34,4	0,008	0,008
10	26,553	-1,853	24,7	-0,075	0,075
11	31,000	-0,200	30,8	-0,007	0,007
12	15,098	0,802	15,9	0,050	0,050
13	27,317	1,683	29	0,058	0,058
14	14,859	0,541	15,4	0,035	0,035
15	27,679	0,921	28,6	0,032	0,032
16	14,859	0,741	15,6	0,047	0,047
17	27,958	-0,258	27,7	-0,009	0,009
18	34,733	-0,633	34,1	-0,019	0,019
19	37,617	0,083	37,7	0,002	0,002
20	40,983	0,917	41,9	0,022	0,022
				сумма	0,753
				Е отн	3,763

Относительная ошибка апроксимации Е отн=3,763<15%, следовательно модель имеет высокую точность.