ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО‑ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Филиал в г. Брянске

АУДИТОРНАЯ РАБОТА

по дисциплине

ЭКОНОМЕТРИКА

ВАРИАНТ №3

 

 

 

 

 

ВАРИАНТ 3

По данным, представленным в табл. 3, изучается зависимость индекса человеческого развития[1] Y от переменных:

Ø  X1 — ВВП 1997 г., % к 1990 г.;

Ø  Х2 — расходы на конечное потребление в текущих ценах, % к ВВП;

Ø  X3 — расходы домашних хозяйств, % к ВВП;

Ø  Х4 — валовое накопление, % к ВВП;

Ø  Х5 — суточная калорийность питания населения, ккал на душу населе­ния;

Ø  Х6 — ожидаемая продолжительность жизни при рождении 1997 г., лет.

Таблица 3

Страна

Y

X1

X2

X3

X4

X5

X6

Австрия

0,904

115

75,5

56,1

25,2

3343

77

Австралия

0,922

123

78,5

61,8

21,8

3001

78,2

……………………………………………………………………………………..

Швеция

0,923

105

79

53,1

14,1

3160

78,5

Задание

1.     Постройте матрицу парных коэффициентов корреляции. Установите, какие факторы мультиколлинеарны.

2.     Постройте уравнение множественной регрессии в линейной форме с полным набором факторов.

3.     Оцените статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.

4.     Отберите информативные факторы по пунктам 1 и 3. Постройте уравне­ние регрессии со статистически значимыми факторами.

5.     Проверьте выполнение предпосылок метода наименьших квадратов, в том числе, проведите тестирование ошибок уравнения множественной рег­рессии на гетероскедастичность.

РЕШЕНИЕ.

Для решения задачи используется табличный процессор MS Excel.

         1. С помощью надстройки «Анализ данных… Корреляция» строим матрицу парных коэффициентов корреляции между всеми исследуемыми переменными (меню «Сервис» ® «Анализ данных…» ® «Корреляция»). На рис. 1 изображена панель корреляционного анализа программного средства. Результаты корреляционного анализа приведены в табл. 1.

рис. 1. Панель корреляционного анализа в MS Excel

Таблица 1

Матрица парных коэффициентов корреляции

 

Y

X1

X2

X3

X4

X5

X6

Y

1

X1

-0,116

1

X2

0,252

-0,656

1

X3

0,066

-0,439

0,799

1

X4

-0,489

0,657

-0,714

-0,627

1

X5

0,787

-0,053

0,246

0,100

-0,420

1

X6

0,958

0,108

0,107

0,006

-0,382

0,730

1

Анализ значений парных коэффициентов корреляции между факторами Х1, Х2, …, Х6 показывает, что только коэффициент корреляции между парой факторов Х1–Х4 превышает по абсолютной величине 0,8 (выделен в таблице заливкой). Факторы Х1–Х4, таким образом, признаются коллинеарными.

         2. С помощью надстройки «Анализ данных… Регрессия» программного средства строим линейное уравнение множественной регрессии с полным перечнем факторов (меню «Сервис» ® «Анализ данных…» ® «Регрессия»). Панель регрессионного анализа изображена на рис. 2.

Рис. 2. Панель регрессионного анализа модели с полным перечнем факторов

Результаты регрессионного анализа приведены в прил. 2 и перенесены в табл. 2. Уравнение регрессии с полным перечнем факторов имеет вид:

.

 

 

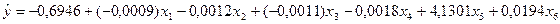Таблица 2

Результаты регрессионного анализа модели с полным перечнем факторов

Регрессионная статистика

Множественный R

0,990

R-квадрат

0,980

Нормированный R-квадрат

0,970

Стандартная ошибка

0,019

Наблюдения

19

 

 

Дисперсионный анализ

 

df

SS

MS

F

Значимость F

Регрессия

6

0,206270804

0,034378467

98,92

1,63E-09

Остаток

12

0,004170354

0,00034753

Итого

18

0,210441158

 

 

 

Уравнение регрессии

 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Y-пересечение

-0,6946

0,1421

-4,8894

0,0004

X1

-0,0009

0,0002

-3,4644

0,0047

X2

0,0012

0,0013

0,9042

0,3837

X3

-0,0011

0,0013

-0,8510

0,4114

X4

0,0018

0,0016

1,1308

0,2803

X5

4,1301

1,9732

2,0931

0,0583

X6

0,0194

0,0015

13,3341

1,4817

3. Проверим статистическую значимость уравнения регрессии. Табличное значение F-критерия Фишера можно определить с помощью встроенной функции MS Excel «FРАСПОБР», которая имеет следующий синтаксис:

=FРАСПОБР(«Уровень значимости a»;«dfрег»;«dfост»)

         Для уровня значимости a=0,05 и чисел степеней свободы числителя (регрессии) 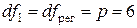 (где p=6 — число факторов в модели) и знаменателя (остатка) 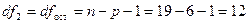 табличное значение

F-критерия Фишера составляет Fтабл=3,00.

         Видно, что расчетное значение F-статистики Фишера

 

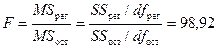
превышает табличное (см. «F» в табл. 2), что свидетельствует о статистической значимости уравнения регрессии в целом. На этот же факт указывает и то, что вероятность случайного формирования уравнения регрессии в том виде, в каком оно имеется, составляет 1,63×10-9 (см. «Значимость F» в табл. 2), что ниже допустимого уровня значимости a=0,05.

         Проверим статистическую значимость коэффициентов уравнения регрессии при факторах Х1, Х2, …, Х6 с помощью t-критерия Стьюдента:

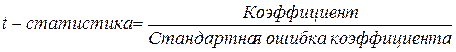
Табличное значение t-критерия Стьюдента можно определить с помощью встроенной функции MS Excel «СТЬЮДРАСПОБР»:

=СТЬЮДРАСПОБР(«Уровень значимости a»;«dfост»)

         Для уровня значимости a=0,05 и числа степеней свободы остатка df=dfост=12 табличное значение t-критерия Стьюдента составляет 2,179. Анализ данных в табл. 2 показывает, что табличное значение t‑критерия Стьюдента превышают по абсолютной величине t-статистики коэффициентов при факторах Х1, Х3, и эти коэффициенты признаются статистически значимыми. На этот же факт указывают и значения вероятности случайного формирования коэффициентов, которые ниже допустимого уровня значимости a=0,05 (см. «P-Значение» в табл. 2).

         Что касается факторов Х2, Х4, Х5 и Х6 (выделены в табл. 2 заливкой), то t‑статистики их коэффициентов меньше по абсолютной величине табличного значения t-критерия Стьюдента, а «P-Значение» выше уровня значимости a=0,05. Таким образом эти коэффициенты не являются статистически значимыми.

 4. По результатам проверки статистической значимости коэффициентов уравнения регрессии Y=f(X1, X2, X3, X4, X6), проведенной в предыдущем пункте, строим новую регрессионную модель, содержащую только информативные факторы. Такими факторами будем считать либо факторы, коэффициенты при которых статистически значимы, либо факторы, у коэффициентов которых t‑статистика превышает по абсолютной величине единицу (другими словами, абсолютная величина коэффициента больше его стандартной ошибки). К первой группе относятся факторы Х1, Х2, Х6, ко второй — фактор X4. Фактор X3 исключается из рассмотрения как неинформативный (÷tb4ç<1), и окончательно регрессионная модель будет содержать факторы X1, X2, X4, X6.

        

Для построения уравнения регрессии Y=f(X1, X2, X4, X6) скопируем на чистый рабочий лист MS Excel значения переменных Y, X1, X2, X4, X6

(прил. 5). Проводим регрессионный анализ (рис. 3). Его результаты приведены в прил. 5 и перенесены в табл. 2. Само уравнение регрессии имеет вид:

.

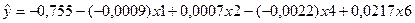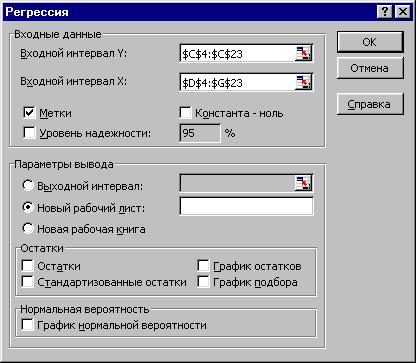
рис. 4. Панель регрессионного анализа модели Y=f(X1, X2, X4, X6)

 

Таблица 3

Результаты регрессионного анализа модели Y=f(X1, X2, X4, X6).

Регрессионная статистика

Множественный R

0,985

R-квадрат

0,971

Нормированный R-квадрат

0,963

Стандартная ошибка

0,021

Наблюдения

19

Дисперсионный анализ

 

df

SS

MS

F

Значимость F

Регрессия

4

0,2043

0,0511

116,55

1,39E-10

Остаток

14

0,0061

0,0004

Итого

18

0,2104

Уравнение регрессии

 

Коэффициенты

Стандартная ошибка

t-статистика

P-Значение

Y-пересечение

-0,7558

0,1517

-4,9814

0,0002

X1

-0,0009

0,0003

-3,7390

0,0022

X2

0,0007

0,0011

0,6300

0,5388

X4

0,0022

0,0016

1,3452

0,1999

X6

0,0217

0,0012

17,7562

5,361

Уравнение регрессии статистически значимо в целом. Вероятность его случайного формирования ниже допустимого уровня значимости a=0,05 (см. «Значимость F» в табл. 3).

         Статистически значимыми являются коэффициенты при факторах Х2, Х3, Х6: вероятность их случайного формирования ниже допустимого уровня значимости a=0,05 (см. «P-Значение» в табл. 3). Это свидетельствует о существенном влиянии изменения данных факторов на изменение годовой прибыли Y.

         Коэффициент при факторе Х1 (выделен в табл. 3 заливкой) не является статистически значимым. Однако этот фактор можно считать информативным, так как t‑статистика его коэффициента превышает по абсолютной величине единицу, хотя к дальнейшим выводам относительно фактора Х1 следует относиться с некоторой осторожностью.

[1]Специальный индекс человеческого развития, который объединяет три показателя (валовой внутренний продукт на душу населения, грамотность и продолжительность предстоящей жизни) и дает обобщенную оценку человеческого прогресса. Впервые данный показатель был предложен в 1990 г. группой исследователей Программы развития ООН.