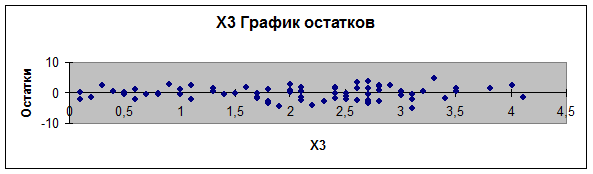
Рис. 3. График остатков (е_i от х₃)

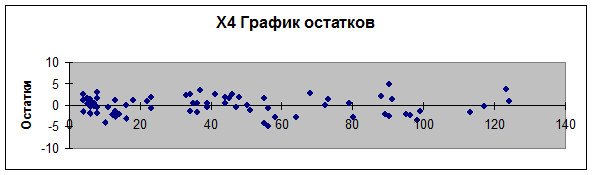
Рис. 4. График остатков (е_i от х₄)

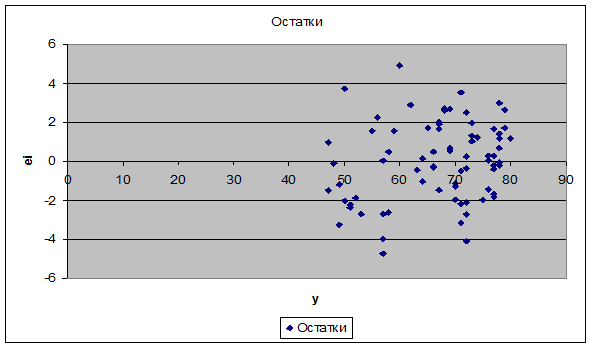
Рис. 5. График остатков (е_i от у)

4.

. Для проверки предпосылок МНК рассмотрим графики остатков (рис. 1-5). На графике е_i от у (рис. 5) остаточная величина е_i обнаруживает тенденцию к уменьшению по мере роста у, а на графиках остатков е_i от х_i (рис. 1-4) наблюдается некоторая синусоидальная зависимость. Это дает повод усомниться в случайности остаточной компоненты и выполнение предпосылки о равенстве дисперсий. Проверим наличие гетероскедастичности  при помощи метода Голдфельда-Квандта:

·     упорядочим все наблюдения по мере возрастания х₁;

·     разделим совокупность на 2 группы, исключив из рассмотрения 10 центральных наблюдения, тогда в каждой группе будет по 33 наблюдений;

·     определим по каждой из групп уравнения регрессии (применим инструмент Регрессия). Остаточные суммы квадратов для первой регрессии S_1у=155,25, для второй – S_2у=74,71. Так как S_1у> S_2у, то F_набл= S_1у / S_2у=2,078. Табличное значение F-критерия при доверительной вероятности 0,95 при v1=n1-m=33-4=29 и v2=n-n1-m=76-33-4=39 составляет 1,759. Так как F_набл>F_табл, то наличие гетероскедастичности подтверждается.

Предпосылка о равенстве математического ожидания остаточной компоненты нулю выполняется, так как на графиках остатков (е_i от х_i) (рис. 1-4) остатки расположены у оси ох_i симметрично.

Предпосылка о независимости остатков принимается как аксиома, так как дана пространственная выборка.

Проверим предпосылку о нормальности ряда остатков с помощью RS-критерия.

R=ε_max- ε_min=4,928-(-7,701)=9,629

S=2,079

RS=9,629/2,079=4,633.

Значение RS-критерия попадает в критический интервал (3,83; 5,14) для n=50 и α=0,05, значит остатки распределены по нормальному закону.

5.

Проверка значимости уравнения регрессии с помощью F-критерия: табличное значение F-критерия при доверительной вероятности 0,95 при v1=k=4 и v₂=n-k-1=76-4-1=71 составляет 2,501. Так как для регрессионной модели выполняется неравенство F_расч>F_табл, то данное линейного уравнения регрессии является значимым (табл. 5).

Оценка значимости параметров регрессионной модели с помощью t-критерия: табличное значение t-критерия при 5%-ном уровне значимости и степенях свободы (76-4-1=71) составляет 1,994. Так как для всех параметров регрессионной модели выполняется неравенство |t_расч|>t_табл, то все коэффициенты линейного уравнения регрессии являются значимыми, следовательно, все факторы регрессионной модели значимо воздействуют на формирование средней ожидаемой продолжительности жизни (табл. 6).

6.

Так как все факторы модели множественной регрессии значимы, то строить модель с исключением некоторых из них является нецелесообразным.

7.

Прогнозные значения факторов:

Х₁=0.8∙X_1max=0,8∙100=80

X₂=0.8∙X_2max=0.8∙3,5=2,8

X₃=0.8∙X_3max=0.8∙4,1=3,28

X₄=0.8∙X_4max=0,8∙124=99,2

Что бы определить прогнозные значения результата подставим прогнозные значения факторов в регрессионную модель:

Y^*_прог = 72,71 + 0,0766∙80 - 2,458∙2,8 + 2,347∙3,28 - 0,21∙99,2=58,82.

8.

Ошибка прогноза рассчитывается по формуле:

X*=

1

80

2,8

3,28

99,2

	1
	80
X*т=	2,8
	3,28
	99,2

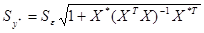
	76	2260,7	133,3	155,4	3107
ХТХ=	2260,7	129277,8	2715,08	3199,31	36692,5
	133,3	2715,08	298,81	333,79	7236
	155,4	3199,31	333,79	393,24	7801,2
	3107	36692,5	7236	7801,2	217631

	0,3111281	-0,0035825	0,0606372	-0,1008839	-0,0022376
(ХТХ)-1=	-0,0035825	0,0000531	-0,0010234	0,0011787	0,0000340
	0,0606372	-0,0010234	0,1262301	-0,0892104	-0,0016923
	-0,1008839	0,0011787	-0,0892104	0,0867868	0,0010967
	-0,0022376	0,0000340	-0,0016923	0,0010967	0,0000478

X*(ХТХ)-1=

-0,3586

0,005033

-0,1283

0,13708

0,004077

X*(ХТХ)-1Х*Т=

0,539043576

Таким образом, S_y*=2.578.

t_(0.05;74)=1,994

Доверительный интервал: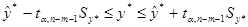

58,82-1,994∙2,578≤y^*≤58,82+1,994∙2,578

53,68≤y^*≤63,96 – доверительный интервал для уровня значимости 5 %.