Таблица 2

	Y	X1	X2	X3	X4
Y	1
X1	0,780235	1
X2	-0,72516	-0,62251	1
X3	-0,53397	-0,65771	0,874008	1
X4	-0,96876	-0,74333	0,736073	0,55373	1

Оценку статистической значимости коэффициентов корреляции проведем с помощью t-критерия Стьюдента: рассчитаем t для каждого коэффициента корреляции (табл. 3) по формуле .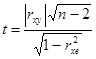

Таблица 3

	Y	X1	X2	X3	X4
Y	-
X1	10,73057	-
X2	9,059288	6,842452	-
X3	5,432741	7,510929	15,47295	-
X4	33,60338	9,559118	9,35428	5,72041	-

Табличное значение t-критерия определим с помощью функции СТЬЮДРАСПОБР (0.05,74). Табличное значение t-критерия при 5%-ном уровне значимости и степенях свободы (76-2=74) составляет 1,993. Все коэффициенты парной корреляции являются значимыми, так как для них выполняется неравенство |t_расч|>t_табл.

В качестве критерия мультиколлинеарности может быть принято соблюдение следующих неравенств:

r_yxi>r_xixk,      r_yxk>r_xixk,     r_xixk<0.8.

Анализ матрицы коэффициентов парной корреляции (табл. 2) показывает, что мультиколлинеарны факторы Х₂ и Х₃ (r_x2x3=0.874, нарушается r_xixk<0.8), Х₂ и Х₄ (r_yx2<r_x2x4, нарушается r_yxi>r_xixk), Х₁ и Х₃ (r_yx3<r_x1x3, нарушается r_yxk>r_xixk).

2.

Хотя имеет место мультиколлинеарность факторов модели, но использование метода исключения показало, что наиболее целесообразной для описания средней ожидаемой продолжительности жизни является модель с полным набором факторов.

Для расчета параметров линейного уравнения множественной регрессии применим инструмент Регрессия (Анализ данных в Excel):

·     выберем команду Сервис => Анализ данных => Регрессия;

·     в диалоговом окне Регрессия в поле Входной интервал Y введем диапазон ячеек, содержащих значения зависимой переменной. В поле Входной интервал Х введем диапазон ячеек, содержащих значения независимых переменных. Так как введены заголовки столбцов, то установим флажок Метки;

·     выберем в качестве параметра вывода Новый рабочий лист;

·     в поле Остатки поставим флажки Остатки и График остатков и нажмем ОК.