ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

Аудиторная работа

по дисциплине «Эконометрика»

Выполнила: студентка 3 курса

специальности: ФК

Вариант №5

Проверил:

Пенза 2006

Изучается зависимость средней ожидаемой продолжительности жизни от нескольких факторов по данным за 1995 г., представленным в табл. 1.

Таблица 1

Страна	Y	X1	X2	X3	X4
Мозамбик	47	3	2,6	2,4	113
Бурунди	49	2,3	2,6	2,7	98
...............................................................................................................................
Швейцария	78	95,9	1	0,8	6

Принятые в таблице обозначения:

Y – средняя ожидаемая продолжительность жизни при рождении, лет;

Х₁ – ВВП в паритетах покупательной способности;

Х₂ – цепные темпы прироста населения, %;

Х₃ – цепные темпы прироста рабочей силы, %;

Х₄ – коэффициент младенческой смертности, %;

Задание

1.     Рассчитайте матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов корреляции. Установите, какие факторы коллинеарны.

2.     Постройте уравнение множественной регрессии, обосновав отбор факторов.

3.     Постройте график остатков.

4.     Проверьте выполнение предпосылок МНК.

5.     Оцените статистическую значимость уравнения множественной регрессии. Какие факторы значимо воздействуют на формирование средней ожидаемой продолжительности жизни в этом уравнении?

6.     Постройте уравнение множественной регрессии только со статистически значимыми факторами.

7.     Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.

8.     Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (а=0,05; а=0,1).

Решение

1.

Для расчета матрицы парных коэффициентов корреляции используем инструмент Корреляция (Анализ данных в Excel):

·     выберем команду Сервис => Анализ данных => Корреляция ;

·     в диалоговом окне Корреляция в поле Входной интервал введем диапазон ячеек, содержащих исходные данные. Так как введены заголовки столбцов, то установим флажок Метки в первой строке ;

·     выберем в качестве параметра вывода Новый рабочий лист и нажмем ОК.

В результате получим матрицу парных коэффициентов корреляции (табл.2).

Таблица 2

	Y	X1	X2	X3	X4
Y	1
X1	0,780235	1
X2	-0,72516	-0,62251	1
X3	-0,53397	-0,65771	0,874008	1
X4	-0,96876	-0,74333	0,736073	0,55373	1

Оценку статистической значимости коэффициентов корреляции проведем с помощью t-критерия Стьюдента: рассчитаем t для каждого коэффициента корреляции (табл. 3) по формуле .

Таблица 3

	Y	X1	X2	X3	X4
Y	-
X1	10,73057	-
X2	9,059288	6,842452	-
X3	5,432741	7,510929	15,47295	-
X4	33,60338	9,559118	9,35428	5,72041	-

Табличное значение t-критерия определим с помощью функции СТЬЮДРАСПОБР (0.05,74). Табличное значение t-критерия при 5%-ном уровне значимости и степенях свободы (76-2=74) составляет 1,993. Все коэффициенты парной корреляции являются значимыми, так как для них выполняется неравенство |t_расч|>t_табл.

В качестве критерия мультиколлинеарности может быть принято соблюдение следующих неравенств:

r_yxi>r_xixk,      r_yxk>r_xixk,     r_xixk<0.8.

Анализ матрицы коэффициентов парной корреляции (табл. 2) показывает, что мультиколлинеарны факторы Х₂ и Х₃ (r_x2x3=0.874, нарушается r_xixk<0.8), Х₂ и Х₄ (r_yx2<r_x2x4, нарушается r_yxi>r_xixk), Х₁ и Х₃ (r_yx3<r_x1x3, нарушается r_yxk>r_xixk).

2.

Хотя имеет место мультиколлинеарность факторов модели, но использование метода исключения показало, что наиболее целесообразной для описания средней ожидаемой продолжительности жизни является модель с полным набором факторов.

Для расчета параметров линейного уравнения множественной регрессии применим инструмент Регрессия (Анализ данных в Excel):

·     выберем команду Сервис => Анализ данных => Регрессия;

·     в диалоговом окне Регрессия в поле Входной интервал Y введем диапазон ячеек, содержащих значения зависимой переменной. В поле Входной интервал Х введем диапазон ячеек, содержащих значения независимых переменных. Так как введены заголовки столбцов, то установим флажок Метки;

·     выберем в качестве параметра вывода Новый рабочий лист;

·     в поле Остатки поставим флажки Остатки и График остатков и нажмем ОК.

Результат регрессионного анализа содержится в табл. 4-6. По результатам таблицы 6 запишем полученное уравнение линейной регрессии:

Y= 72,71 + 0,0766Х₁ - 2,458Х₂ + 2,347Х₃ - 0,21Х₄.

Таблица 4

Регрессионная статистика
Множественный R	0,977623
R-квадрат	0,955746
Нормированный R-квадрат	0,953253
Стандартная ошибка	2,078503
Наблюдения	76

Таблица 5

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	4	6624,425478	1656,106369	383,3424367	2,98228E-47
Остаток	71	306,7324172	4,32017489
Итого	75	6931,157895

Таблица 6

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	72,71049	1,159365267	62,71577539	6,43661E-64
X1	0,076553	0,015140742	5,056125037	3,21233E-06
X2	-2,45833	0,738468693	-3,328950654	0,001384522
X3	2,347473	0,612318576	3,833744409	0,00027026
X4	-0,2099	0,014365344	-14,61166534	4,31396E-23

3.

Графики остатков (зависимость е_i от х_i) строятся инструментом Регрессия, так как поставлен флажок График остатков (рис. 1, 2, 3, 4). График остатков (е_i от у) построим с помощью Мастера диаграмм Excel (рис. 5).

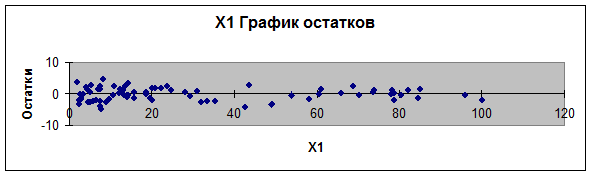
Рис. 1. График остатков (е_i от х₁)

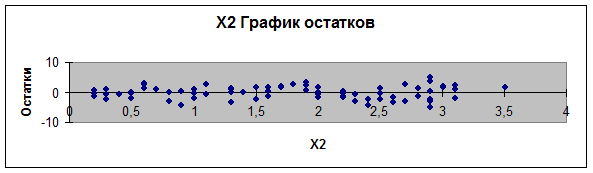
Рис. 2. График остатков (е_i от х₂)

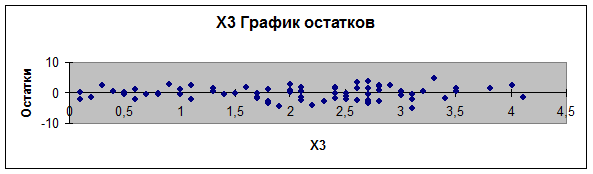
Рис. 3. График остатков (е_i от х₃)

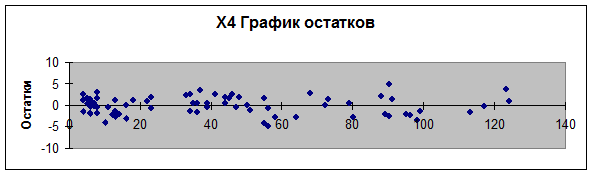
Рис. 4. График остатков (е_i от х₄)

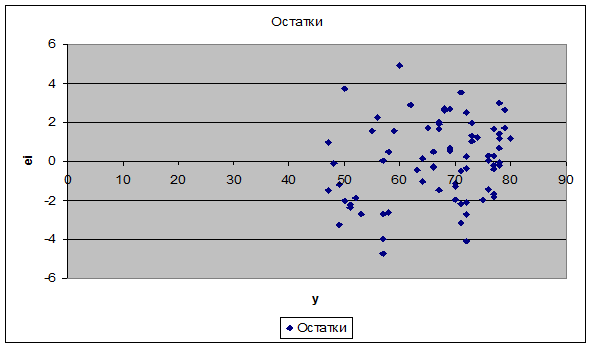
Рис. 5. График остатков (е_i от у)

4.

. Для проверки предпосылок МНК рассмотрим графики остатков (рис. 1-5). На графике е_i от у (рис. 5) остаточная величина е_i обнаруживает тенденцию к уменьшению по мере роста у, а на графиках остатков е_i от х_i (рис. 1-4) наблюдается некоторая синусоидальная зависимость. Это дает повод усомниться в случайности остаточной компоненты и выполнение предпосылки о равенстве дисперсий. Проверим наличие гетероскедастичности  при помощи метода Голдфельда-Квандта:

·     упорядочим все наблюдения по мере возрастания х₁;

·     разделим совокупность на 2 группы, исключив из рассмотрения 10 центральных наблюдения, тогда в каждой группе будет по 33 наблюдений;

·     определим по каждой из групп уравнения регрессии (применим инструмент Регрессия). Остаточные суммы квадратов для первой регрессии S_1у=155,25, для второй – S_2у=74,71. Так как S_1у> S_2у, то F_набл= S_1у / S_2у=2,078. Табличное значение F-критерия при доверительной вероятности 0,95 при v1=n1-m=33-4=29 и v2=n-n1-m=76-33-4=39 составляет 1,759. Так как F_набл>F_табл, то наличие гетероскедастичности подтверждается.

Предпосылка о равенстве математического ожидания остаточной компоненты нулю выполняется, так как на графиках остатков (е_i от х_i) (рис. 1-4) остатки расположены у оси ох_i симметрично.

Предпосылка о независимости остатков принимается как аксиома, так как дана пространственная выборка.

Проверим предпосылку о нормальности ряда остатков с помощью RS-критерия.

R=ε_max- ε_min=4,928-(-7,701)=9,629

S=2,079

RS=9,629/2,079=4,633.

Значение RS-критерия попадает в критический интервал (3,83; 5,14) для n=50 и α=0,05, значит остатки распределены по нормальному закону.

5.

Проверка значимости уравнения регрессии с помощью F-критерия: табличное значение F-критерия при доверительной вероятности 0,95 при v1=k=4 и v₂=n-k-1=76-4-1=71 составляет 2,501. Так как для регрессионной модели выполняется неравенство F_расч>F_табл, то данное линейного уравнения регрессии является значимым (табл. 5).

Оценка значимости параметров регрессионной модели с помощью t-критерия: табличное значение t-критерия при 5%-ном уровне значимости и степенях свободы (76-4-1=71) составляет 1,994. Так как для всех параметров регрессионной модели выполняется неравенство |t_расч|>t_табл, то все коэффициенты линейного уравнения регрессии являются значимыми, следовательно, все факторы регрессионной модели значимо воздействуют на формирование средней ожидаемой продолжительности жизни (табл. 6).

6.

Так как все факторы модели множественной регрессии значимы, то строить модель с исключением некоторых из них является нецелесообразным.

7.

Прогнозные значения факторов:

Х₁=0.8∙X_1max=0,8∙100=80

X₂=0.8∙X_2max=0.8∙3,5=2,8

X₃=0.8∙X_3max=0.8∙4,1=3,28

X₄=0.8∙X_4max=0,8∙124=99,2

Что бы определить прогнозные значения результата подставим прогнозные значения факторов в регрессионную модель:

Y^*_прог = 72,71 + 0,0766∙80 - 2,458∙2,8 + 2,347∙3,28 - 0,21∙99,2=58,82.

8.

Ошибка прогноза рассчитывается по формуле:

X*=

1

80

2,8

3,28

99,2

	1
	80
X*т=	2,8
	3,28
	99,2

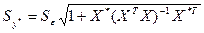
	76	2260,7	133,3	155,4	3107
ХТХ=	2260,7	129277,8	2715,08	3199,31	36692,5
	133,3	2715,08	298,81	333,79	7236
	155,4	3199,31	333,79	393,24	7801,2
	3107	36692,5	7236	7801,2	217631

	0,3111281	-0,0035825	0,0606372	-0,1008839	-0,0022376
(ХТХ)-1=	-0,0035825	0,0000531	-0,0010234	0,0011787	0,0000340
	0,0606372	-0,0010234	0,1262301	-0,0892104	-0,0016923
	-0,1008839	0,0011787	-0,0892104	0,0867868	0,0010967
	-0,0022376	0,0000340	-0,0016923	0,0010967	0,0000478

X*(ХТХ)-1=

-0,3586

0,005033

-0,1283

0,13708

0,004077

X*(ХТХ)-1Х*Т=

0,539043576

Таким образом, S_y*=2.578.

t_(0.05;22)=1,994

Доверительный интервал:

58,82-1,994∙2,578≤y^*≤58,82+1,994∙2,578

53,68≤y^*≤63,96 – доверительный интервал для уровня значимости 5 %.