ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Аудиторная работа
по дисциплине «Эконометрика»
студентки 3 курса специальности «Финансы и кредит»
Вариант № 1
Пенза, 2006
|
Имеются данные о
деятельности крупнейших компаний США в |
|||||
|
п/n |
Чистый до-ход, млрд. долл. США |
Оборот капи-тала, млрд. долл. США |
Использо-ванный ка-питал, млрд. долл. |
Числен-ность служа-щих, тыс. чел. |
Рыночная ка-питализация ком-пании, млрд. долл. США |
|
Y |
X1 |
X2 |
X3 |
X4 |
|
|
1 |
0,9 |
31,3 |
18,9 |
43 |
40,9 |
|
2 |
1,7 |
13,4 |
13,7 |
64,7 |
40,5 |
|
3 |
0,7 |
4,5 |
18,5 |
24 |
38,9 |
|
4 |
1,7 |
10 |
4,8 |
50,2 |
38,5 |
|
5 |
2,6 |
20 |
21,8 |
106 |
37,3 |
|
6 |
1,3 |
15 |
5,8 |
96,6 |
26,5 |
|
7 |
4,1 |
137,1 |
99 |
347 |
37 |
|
8 |
1,6 |
17,9 |
20,1 |
85,6 |
36,8 |
|
9 |
6,9 |
165,4 |
60,6 |
745 |
36,3 |
|
10 |
0,4 |
2 |
1,4 |
4,1 |
35,3 |
|
11 |
1,3 |
6,8 |
8 |
26,8 |
35,3 |
|
12 |
1,9 |
27,1 |
18,9 |
42,7 |
35 |
|
13 |
1,9 |
13,4 |
13,2 |
61,8 |
26,2 |
|
14 |
1,4 |
9,8 |
12,6 |
212 |
33,1 |
|
15 |
0,4 |
19,5 |
12,2 |
105 |
32,7 |
|
16 |
0,8 |
6,8 |
3,2 |
33,5 |
32,1 |
|
17 |
1,8 |
27 |
13 |
142 |
30,5 |
|
18 |
0,9 |
12,4 |
6,9 |
96 |
29,8 |
|
19 |
1,1 |
17,7 |
15 |
140 |
25,4 |
|
20 |
1,9 |
12,7 |
11,9 |
59,3 |
29,3 |
|
21 |
-0,9 |
21,4 |
1,6 |
131 |
29,2 |
|
22 |
1,3 |
13,5 |
8,6 |
70,7 |
29,2 |
|
23 |
2 |
13,4 |
11,5 |
65,4 |
29,1 |
|
24 |
0,6 |
4,2 |
1,9 |
23,1 |
27,9 |
|
25 |
0,7 |
15,5 |
5,8 |
80,8 |
27,2 |
Задание
1. Рассчитайте матрицу парных коэффициентов корреляции; оцените статистическую значимость коэффициентов корреляции.
2. Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов.
3. Оцените статистическую значимость параметров регрессионной модели с помощью t-критерия; нулевую гипотезу о значимости уравнения проверите с помощь. F-критерия; оцените качество уравнения регрессии с помощью коэффициента детерминации R2.
4. Дайте сравнительную оценку силы связи факторов с результатом с помощью коэффициентов эластичности, β и ∆ коэффициентов.
5. Оцените точность уравнения через среднюю относительную ошибку аппроксимации.
6. Отберите информативные факторы в модели по t-критерию для коэффициентов регрессии. Постройте модель только с информативными факторами и оцените ее параметры.
7. Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
8. Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (а=0,05; а=0,1).
Решение
1.
Для расчета матрицы парных коэффициентов корреляции используем инструмент Корреляция (Анализ данных в Excel):
Ø выберем команду Сервис => Анализ данных => Корреляция;
Ø в диалоговом окне Корреляция в поле Входной интервал введем диапазон ячеек, содержащих исходные данные. Так как введены заголовки столбцов, то установим флажок Метки в первой строке;
Ø выберем в качестве параметра вывода Новый рабочий лист и нажмем ОК.
В результате получим матрицу парных коэффициентов корреляции (табл. 1).
Таблица 1
|
|
Y |
X1 |
X2 |
X3 |
X4 |
|
Y |
1 |
||||
|
X1 |
0,848 |
1 |
|||
|
X2 |
0,763 |
0,898 |
1 |
||
|
X3 |
0,830 |
0,912 |
0,713 |
1 |
|
|
X4 |
0,269 |
0,249 |
0,348 |
0,115 |
1 |
Оценку статистической значимости
коэффициентов корреляции проведем с помощью t-критерия Стьюдента: рассчитаем t
для каждого коэффициента корреляции (табл. 2) по формуле 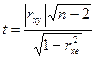 .
.
Таблица 2
|
|
Y |
X1 |
X2 |
X3 |
X4 |
|
Y |
- |
||||
|
X1 |
7,674 |
- |
|||
|
X2 |
5,666 |
9,774 |
- |
||
|
X3 |
7,125 |
10,629 |
4,870 |
- |
|
|
X4 |
1,339 |
1,231 |
1,783 |
0,556 |
- |
Табличное значение t-критерия определим с помощью функции СТЬЮДРАСПОБР (0.05,20). Табличное значение t-критерия при 5%-ном уровне значимости и степенях свободы (25-4-1=20) составляет 2,086. Коэффициент является значимым, если |tрасч|>tтабл и незначимым в противном случае. Результат определения статистической значимости представлен в таблице 3.
Таблица 3
|
|
Y |
X1 |
X2 |
X3 |
X4 |
|
Y |
- |
||||
|
X1 |
значим |
- |
|||
|
X2 |
значим |
значим |
- |
||
|
X3 |
значим |
значим |
значим |
- |
|
|
X4 |
не значим |
не значим |
не значим |
не значим |
- |
2.
Для расчета параметров линейного уравнения множественной регрессии применим инструмент Регрессия (Анализ данных в Excel):
Ø выберем команду Сервис => Анализ данных => Регрессия;
Ø в диалоговом окне Регрессия в поле Входной интервал Y введем диапазон ячеек, содержащих значения зависимой переменной. В поле Входной интервал Х введем диапазон ячеек, содержащих значения независимых переменных. Так как введены заголовки столбцов, то установим флажок Метки;
Ø выберем в качестве параметра вывода Новый рабочий лист;
Ø в поле Остатки поставим флажок Остатки и нажмем ОК.
Результат регрессионного анализа содержится в табл. 4-7. По результатам таблицы 6 запишем полученное уравнение линейной регрессии:
Y= -0,363 + 0,0035Х1 + 0,0174Х2 + 0,0053Х3 + 0,0286Х4.
Таблица 4
|
Регрессионная статистика |
|
|
Множественный R |
0,869743924 |
|
R-квадрат |
0,756454493 |
|
Нормированный R-квадрат |
0,707745392 |
|
Стандартная ошибка |
0,77810933 |
|
Наблюдения |
25 |
Таблица 5
|
Дисперсионный анализ |
|||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
Регрессия |
4 |
37,61092 |
9,40272935 |
15,5300441 |
6,2879E-06 |
|
Остаток |
20 |
12,10908 |
0,60545413 |
||
|
Итого |
24 |
49,72 |
Таблица 6
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
|
Y-пересечение |
-0,3625 |
1,1919 |
-0,3041 |
0,7642 |
|
X1 |
0,0035 |
0,0196 |
0,1789 |
0,8598 |
|
X2 |
0,0174 |
0,0217 |
0,8030 |
0,4314 |
|
X3 |
0,0053 |
0,0032 |
1,6590 |
0,1127 |
|
X4 |
0,0286 |
0,0366 |
0,7824 |
0,4432 |
Таблица 7
|
Наблюдение |
Предсказанное Y |
Остатки |
|
1 |
1,47628 |
-0,576279 |
|
2 |
1,42734 |
0,272661 |
|
3 |
1,21682 |
-0,516824 |
|
4 |
1,12584 |
0,574164 |
|
5 |
1,72027 |
0,879731 |
|
6 |
1,06486 |
0,235143 |
|
7 |
4,75206 |
-0,652058 |
|
8 |
1,56016 |
0,039838 |
|
9 |
6,28577 |
0,614229 |
|
10 |
0,70107 |
-0,301068 |
|
11 |
0,95393 |
0,346074 |
|
12 |
1,2911 |
0,6089 |
|
13 |
0,99388 |
0,906123 |
|
14 |
1,96963 |
-0,569626 |
|
15 |
1,41434 |
-1,014342 |
|
16 |
0,81449 |
-0,014492 |
|
17 |
1,58898 |
0,211024 |
|
18 |
1,16615 |
-0,266155 |
|
19 |
1,43459 |
-0,334589 |
|
20 |
1,04417 |
0,855827 |
|
21 |
1,27494 |
-2,174936 |
|
22 |
1,04746 |
0,252536 |
|
23 |
1,06648 |
0,933521 |
|
24 |
0,60705 |
-0,007051 |
|
25 |
1,00235 |
-0,30235 |
3.
Оценка параметров регрессионной модели с помощью t-критерия:
Табличное значение t-критерия определим с помощью функции СТЬЮДРАСПОБР (0.05,20). Табличное значение t-критерия при 5%-ном уровне значимости и степенях свободы (25-4-1=20) составляет 2,086. Так как для всех параметров регрессионной модели выполняется неравенство |tрасч|<tтабл, то все коэффициенты линейного уравнения регрессии являются незначимыми (табл. 6).
Проверка значимости уравнения регрессии с помощью F-критерия:
Табличное значение F-критерия определим с помощью функции FРАСПОБР (0.05;4;20). Табличное значение F-критерия при доверительной вероятности 0,95 при v1=k=4 и v2=n-k-1=25-4-1=20 составляет 2,866. Так как для регрессионной модели выполняется неравенство Fрасч>Fтабл, то данное линейного уравнения регрессии является значимым (табл. 5).
Оценка качества уравнения регрессии с помощью коэффициента детерминации R2:
Для данной модели около 75,7% вариации зависимой переменной Y учтено в модели и обусловлено влиянием включенных факторов Х1, Х2, .Х3, Х4 (R2=0,757 – табл. 4). Данный результат говорит о не очень высоком качестве модели.
4.
Коэффициент эластичности рассчитывается по формуле:
![]()
Полученные значения представлены в табл. 8. Коэффициент эластичности Эj показывает, на сколько % изменится зависимая переменная Y при изменение фактора Xj на 1%.
Э1=0,065 – при изменение Х1 (оборот капитала) на 1% Y (чистый доход) изменится на 0,065%.
Э2=0,182 – при изменение Х2 (использованный капитал) на 1% Y (чистый доход) изменится на 0,182%.
Э3=0,388 – при изменение Х3 (численность служащих) на 1% Y (чистый доход) изменится на 0,388%.
Э4=0,568 – при изменение Х4 (рыночная капитализация компании)) на 1% Y (чистый доход) изменится на 0,568%.
Бетта-коэффициент рассчитывается по формуле:
![]() , где
, где 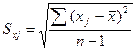 ;
; 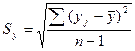 .
.
Полученные значения представлены в табл. 8. Бетта-коэффициент βj показывает, на какую часть величины среднеквадратического отклонения Sу изменится зависимая переменная Y с изменением независимой переменной Хj на величину своего среднеквадратического отклонения при фиксированном на постоянном уровне значение остальных независимых переменных.
β1=0,108 – при увеличении Х1 (оборот капитала) на 38,745 млрд. долл. США (Sх1=38,745) Y(чистый доход) увеличится на 0,155 млрд. долл. США (β1∙Sу=0,108∙1,439=0,155).
β2=0,251 – при увеличении Х2 (использованный капитал) на 20,77 млрд. долл. США (Sх2=20,77) Y(чистый доход) увеличится на 0,36 млрд. долл. США (β1∙Sу=0,251∙1,439=0,36).
β3=0,55 – при увеличении Х3 (численность служащих) на 149,39 тыс. чел. (Sх3=149,39) Y(чистый доход) увеличится на 0,792 тыс. чел. (β1∙Sу=0,55∙1,439=0,792).
β4=0,089 – при увеличении Х4 (рыночная капитализация компании)на 4,736 млрд. долл. США (Sх1=4,736) Y(чистый доход) увеличится на 0,128 млрд. долл. США (β1∙Sу=0,089∙1,439=0,128).
∆–коэффициент рассчитывается по формуле:
![]()
Полученные значения представлены в табл. 8. Коэффициент ∆j показывает долю влияния фактора Хj в суммарном влияние всех факторов на зависимую переменную Y. Следовательно самое сильное влияние на Y оказывает фактор Х3 (численность служащих) (∆3=0,603), а самое слабое влияние на Y оказывает фактор Х4 (рыночная капитализация компании) (∆4=0,032).
5.
Средняя ошибка аппроксимации рассчитывается по формуле:
![]()
Расчетные значения представлены в табл. 9. Средняя ошибка аппроксимации равна 29,2%, следовательно, в среднем расчетные значения отклоняются от фактических на 29,2%. Это говорит о неточности модели.
Таблица 8
|
п/n |
Y |
X1 |
X2 |
X3 |
X4 |
(x1- |
(x2- |
(x3- |
(x4- |
|
1 |
0,9 |
31,3 |
18,9 |
43 |
40,9 |
33,50094 |
6,471936 |
5076,848 |
65,61 |
|
2 |
1,7 |
13,4 |
13,7 |
64,7 |
40,5 |
146,7005 |
7,054336 |
2455,401 |
59,29 |
|
3 |
0,7 |
4,5 |
18,5 |
24 |
38,9 |
441,5041 |
4,596736 |
8145,424 |
37,21 |
|
4 |
1,7 |
10 |
4,8 |
50,2 |
38,5 |
240,6221 |
133,5411 |
4102,659 |
32,49 |
|
5 |
2,6 |
20 |
21,8 |
106 |
37,3 |
30,38214 |
29,63714 |
68,0955 |
20,25 |
|
6 |
1,3 |
15 |
5,8 |
96,6 |
26,5 |
110,5021 |
111,4291 |
311,5931 |
39,69 |
|
7 |
4,1 |
137,1 |
99 |
347 |
37 |
12451,88 |
6830,031 |
54171,63 |
17,64 |
|
8 |
1,6 |
17,9 |
20,1 |
85,6 |
36,8 |
57,94254 |
14,01754 |
820,9371 |
16 |
|
9 |
6,9 |
165,4 |
60,6 |
745 |
36,3 |
19568,65 |
1957,532 |
397843 |
12,25 |
|
10 |
0,4 |
2 |
1,4 |
4,1 |
35,3 |
552,8141 |
223,6819 |
12133,46 |
6,25 |
|
11 |
1,3 |
6,8 |
8 |
26,8 |
35,3 |
350,1389 |
69,82274 |
7647,852 |
6,25 |
|
12 |
1,9 |
27,1 |
18,9 |
42,7 |
35 |
2,521744 |
6,471936 |
5119,689 |
4,84 |
|
13 |
1,9 |
13,4 |
13,2 |
61,8 |
26,2 |
146,7005 |
9,960336 |
2751,212 |
43,56 |
|
14 |
1,4 |
9,8 |
12,6 |
212 |
33,1 |
246,8669 |
14,10754 |
9554,672 |
0,09 |
|
15 |
0,4 |
19,5 |
12,2 |
105 |
32,7 |
36,14414 |
17,27234 |
85,5995 |
0,01 |
|
16 |
0,8 |
6,8 |
3,2 |
33,5 |
32,1 |
350,1389 |
173,0803 |
6520,886 |
0,49 |
|
17 |
1,8 |
27 |
13 |
142 |
30,5 |
2,214144 |
11,26274 |
769,9515 |
5,29 |
|
18 |
0,9 |
12,4 |
6,9 |
96 |
29,8 |
171,9245 |
89,41594 |
333,1355 |
9 |
|
19 |
1,1 |
17,7 |
15 |
140 |
25,4 |
61,02734 |
1,838736 |
662,9595 |
54,76 |
|
20 |
1,9 |
12,7 |
11,9 |
59,3 |
29,3 |
164,1473 |
19,85594 |
3019,722 |
12,25 |
|
21 |
-0,9 |
21,4 |
1,6 |
131 |
29,2 |
16,90854 |
217,7395 |
280,4955 |
12,96 |
|
22 |
1,3 |
13,5 |
8,6 |
70,7 |
29,2 |
144,2881 |
60,15554 |
1896,777 |
12,96 |
|
23 |
2 |
13,4 |
11,5 |
65,4 |
29,1 |
146,7005 |
23,58074 |
2386,518 |
13,69 |
|
24 |
0,6 |
4,2 |
1,9 |
23,1 |
27,9 |
454,2013 |
208,9759 |
8308,687 |
24,01 |
|
25 |
0,7 |
15,5 |
5,8 |
80,8 |
27,2 |
100,2401 |
111,4291 |
1119,036 |
31,36 |
|
Сумма |
39 |
637,8 |
408,9 |
2856,3 |
820 |
36028,67 |
10352,96 |
535586,3 |
538,2 |
|
Sxj |
38,74525 |
20,76953 |
149,3857 |
4,7355 |
|||||
|
Ср знач |
1,56 |
25,512 |
16,356 |
114,252 |
32,8 |
||||
|
bj |
-0,363 |
0,004 |
0,0174 |
0,0053 |
0,027 |
||||
|
Эj |
- |
0,065415 |
0,182432 |
0,388164 |
0,567692 |
||||
|
Бетта |
0,107676 |
0,251082 |
0,550079 |
0,088832 |
|||||
|
Дельта |
0,120711 |
0,253354 |
0,603246 |
0,031587 |
Таблица 9
|
Наблюдение |
Остатки |
Y |
|
|
1 |
-0,576279 |
0,9 |
64,0309738 |
|
2 |
0,272661 |
1,7 |
16,038854 |
|
3 |
-0,516824 |
0,7 |
73,8320419 |
|
4 |
0,574164 |
1,7 |
33,7743428 |
|
5 |
0,879731 |
2,6 |
33,8358064 |
|
6 |
0,235143 |
1,3 |
18,087928 |
|
7 |
-0,652058 |
4,1 |
15,9038496 |
|
8 |
0,039838 |
1,6 |
2,4898738 |
|
9 |
0,614229 |
6,9 |
8,90187252 |
|
10 |
-0,301068 |
0,4 |
75,2670823 |
|
11 |
0,346074 |
1,3 |
26,6210461 |
|
12 |
0,6089 |
1,9 |
32,0473499 |
|
13 |
0,906123 |
1,9 |
47,6907004 |
|
14 |
-0,569626 |
1,4 |
40,6875873 |
|
15 |
-1,014342 |
0,4 |
253,585443 |
|
16 |
-0,014492 |
0,8 |
1,81145968 |
|
17 |
0,211024 |
1,8 |
11,7235643 |
|
18 |
-0,266155 |
0,9 |
29,5727335 |
|
19 |
-0,334589 |
1,1 |
30,4172155 |
|
20 |
0,855827 |
1,9 |
45,0435012 |
|
21 |
-2,174936 |
-0,9 |
-241,65958 |
|
22 |
0,252536 |
1,3 |
19,4258446 |
|
23 |
0,933521 |
2 |
46,6760451 |
|
24 |
-0,007051 |
0,6 |
1,17515277 |
|
25 |
-0,30235 |
0,7 |
43,1928146 |
|
Сумма |
730,173506 |
||
|
Ошибка аппроксимации |
29,2069402 |
6.
С учетом значений t-критерия Стьюдента для всех коэффициентов регрессионной модели с полным набором факторов (табл. 6) информативными факторами являются Х2 (использованный капитал) и Х3 (численность служащих). Построим модель по двум выбранным факторам, используя инструмент Регрессия (Анализ данных в Excel).
Результат регрессионного анализа содержится в табл. 10-12. По результатам таблицы 12 запишем полученное уравнение линейной регрессии:
Y= 0,5247+ 0,0243Х2 + 0,0056Х3.
Оценка параметров регрессионной модели с помощью t-критерия: табличное значение t-критерия при 5%-ном уровне значимости и степенях свободы (25-2-1=22) составляет 2,074. Так как для всех параметров регрессионной модели выполняется неравенство |tрасч|>tтабл, то все коэффициенты линейного уравнения регрессии являются значимыми (табл. 12).
Проверка значимости уравнения регрессии с помощью F-критерия: табличное значение F-критерия при доверительной вероятности 0,95 при v1=k=2 и v2=n-k-1=25-2-1=22 составляет 3,443. Так как для регрессионной модели выполняется неравенство Fрасч>Fтабл, то данное линейного уравнения регрессии является значимым (табл. 11).
Оценка качества уравнения регрессии с помощью коэффициента детерминации R2: для данной модели около 74,8% вариации зависимой переменной Y учтено в модели и обусловлено влиянием включенных факторов Х2, .Х3 (R2=0,748 – табл. 10). Данный результат говорит о не очень высоком качестве модели.
Таблица 10
|
Регрессионная статистика |
|
|
Множественный R |
0,865117 |
|
R-квадрат |
0,748427 |
|
Нормированный R-квадрат |
0,725557 |
|
Стандартная ошибка |
0,754026 |
|
Наблюдения |
25 |
Таблица 11
|
Дисперсионный анализ |
|||||
|
|
df |
SS |
MS |
F |
Значимость F |
|
Регрессия |
2 |
37,21179 |
18,60589 |
32,72487 |
2,55E-07 |
|
Остаток |
22 |
12,50821 |
0,568555 |
||
|
Итого |
24 |
49,72 |
Таблица 12
|
|
Коэффициенты |
Стандартная ошибка |
t-статистика |
P-Значение |
|
Y-пересечение |
0,524672 |
0,198571 |
2,64224 |
0,014882 |
|
X2 |
0,024242 |
0,010562 |
2,295282 |
0,031622 |
|
X3 |
0,005591 |
0,001468 |
3,807813 |
0,000963 |
7.
Прогнозные значения факторов:
X2=0.8∙X1max=0.8∙165.4=132.32
X3=0.8∙X3max=0.8∙745=596
Что бы определить прогнозные значения результата подставим прогнозные значения факторов в регрессионную модель:
Y*прог=0,5247+ 0,0243∙132.32 + 0,0056∙596=7,078.
8.
Ошибка прогноза рассчитывается по формуле:
![]()
|
X*= |
1 |
132,32 |
596 |
|
1 |
|
|
X*т= |
132,32 |
|
596 |
|
25 |
408,9 |
2856,3 |
0,069351810 |
-0,000988397 |
-0,000115408 |
||
|
ХТХ= |
408,9 |
17040,93 |
99774,34 |
(ХТХ)-1= |
-0,000988397 |
0,000196193 |
-0,000019435 |
|
2856,3 |
99774,34 |
861924,3 |
-0,000115408 |
-0,000019435 |
0,000003792 |
|
X*(ХТХ)-1= |
-0,13022 |
0,013388 |
-0,00043 |
|
X*(ХТХ)-1Х*Т= |
1,38695252 |
Таким образом, ![]() .
.
t(0.05;22)=2.074
Доверительный интервал: ![]()
7,078-2,074∙1,165≤y*≤7,078+2,074∙1,165
4.662≤y*≤9.494 – доверительный интервал для уровня значимости 5 %.