Задача № 1
По предприятиям легкой промышленности
региона получена информация, характеризующая зависимость объема выпуска
продукции (У, млн. руб.) от объема капиталовложений (Х, млн. руб.):
|
у
|
60
|
68
|
74
|
76
|
84
|
86
|
92
|
|
х
|
50
|
54
|
60
|
62
|
70
|
66
|
74
|
Требуется:
1. Для характеристики У от Х построить
следующие модели:
-
линейную,
-
степенную,
- показательную,
-
гиперболическую.
2. Оценить каждую модель, определив:
-
индекс корреляции,
-
среднюю относительную ошибку,
-
коэффициент детерминации,
-
F – критерий Фишера.
3. Составить сводную таблицу вычислений,
выбрать лучшую модель, дать интерпретацию рассчитанных характеристик.
4. Рассчитать прогнозные значения результативного
признака, если прогнозное значение фактора увеличатся на 110% относительно
среднего уровня.
5. Результаты расчетов отобразить на
графике.
Решение:
1. Для характеристики У от Х построим:
а) линейную модель регрессии
у(х) = a + b*x, где
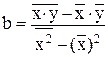
a =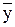 
- b * 
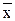
Расчет параметров моделей выполним с применением пакета прикладных
программ обработки электронных таблиц MS Excel в
среде Widows.
Рис. 1.1 Расчет
параметров линейной регрессии
Отсюда модель имеет вид:
у(х) = - 2,063 + 1,272*х
б) степенную модель регрессии
y(х) = a *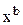 
lgy(x) = lga + b*lgx
Пусть lgy(x) =У, lga = A, lgx = X, тогда
У = A + b*X,где
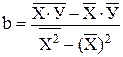
A =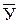 
- b *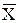 
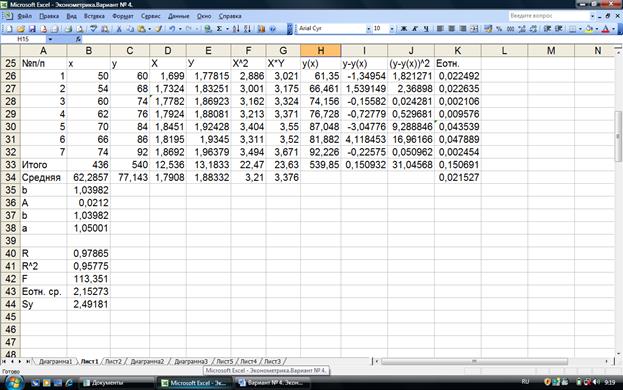
Рис. 1.2 Расчет
параметров степенной регрессии
Отсюда уравнение имеет вид:
y(х) = 1,05*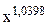
в) показательную модель регрессии
y(х) = а*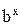
lgy(x) = lga + x*lgb
Пусть
lgy(x) =У, lga = А, lgb = B, тогда
У = A + B*x, где
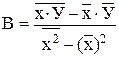
A = 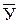- B *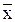 
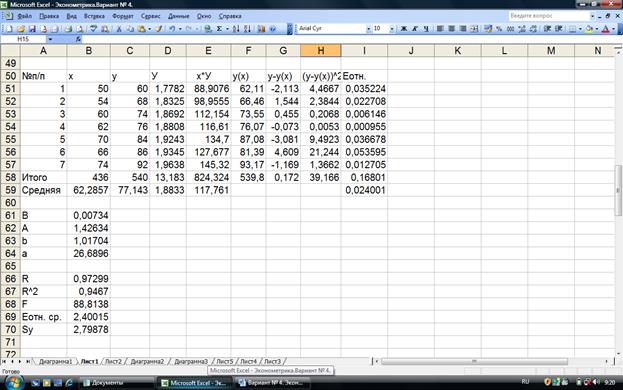
Рис. 1.3 Расчет
параметров показательной регрессии
Отсюда уравнение имеет вид:
y(х) = 26,689*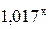
г) гиперболическую модель регрессии
y(х) = a + b/х
Пусть
1/х =X,
тогда
y(x) = a + b*X, где
a =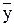 
- b *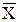 
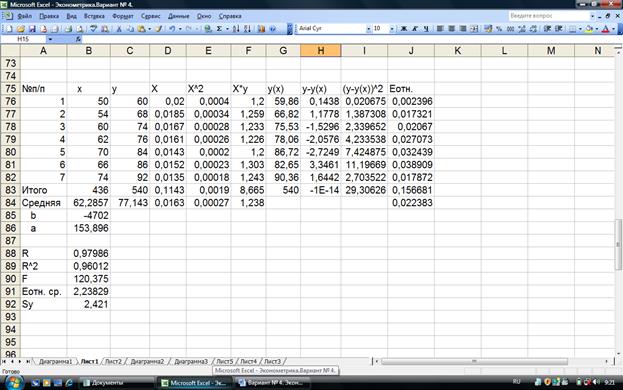
Рис. 1.4 Расчет
параметров гиперболической регрессии
Отсюда уравнение имеет вид:
у(х) = 153,90 - 4702/х
2. Оценим каждую модель, определив:
-
индекс корреляции
-
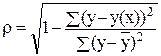
среднюю относительную ошибку
-
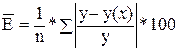
коэффициент детерминации
- F – критерий Фишера.
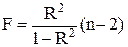
а) для линейной регрессии.
Согласно рис. 1.1 имеем:
R = 0,9789
Между изучаемыми признаками присутствует
прямая и очень тесная связь.
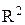= 0,9582
Вариация
выпуска продукции на 95,82% обусловлена вариацией объема
капиталовложений.
F = 114,59
Табличное значение F- критерия найдем с помощью функции FРАСПОБР (рис.
1.5).
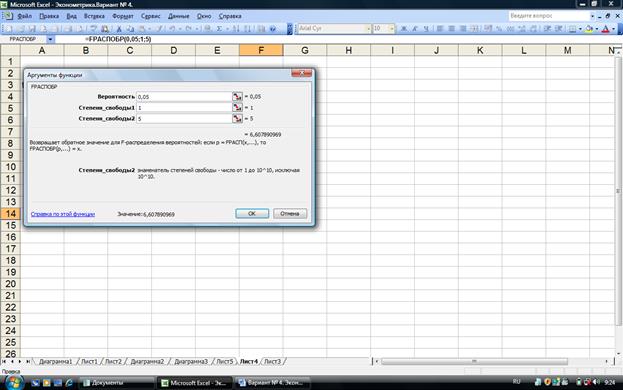
Рис. 1.5
Определение табличного значения F- критерия
Т.к., F > Fтабл., то с вероятностью 0,95 уравнение регрессии
статистически значимо.
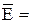2,24%
В среднем расчетные значения у(х)
отличаются от фактических значений на 2,24%.
б) для степенной регрессии
Согласно рис. 1.2 имеем:
r = 0,9787
Между изучаемыми признаками присутствует очень
тесная связь.
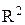= 0,9578
Вариация
выпуска продукции на 95,78% обусловлена вариацией объема капиталовложений.
F = 113,35
Т.к., F > Fтабл., то с
вероятностью 0,95 уравнение регрессии статистически значимо.
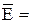2,15%
В среднем расчетные значения у(х)
отличаются от фактических значений на 2,15%.
в) для показательной регрессии
Согласно рис. 1.3 имеем:
r = 0,9730
Между изучаемыми признаками присутствует
очень тесная связь.
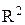= 0,9467
Вариация
выпуска продукции на 94,67% обусловлена вариацией объема
капиталовложений.
F = 88,81
Т.к., F > Fтабл., то с
вероятностью 0,95 уравнение регрессии статистически значимо.
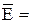2,40%
В среднем расчетные значения у(х)
отличаются от фактических значений на 2,40%.
г) для гиперболической регрессии
Согласно рис. 1.4 имеем:
r = 0,9799
Между изучаемыми признаками присутствует
очень тесная связь.
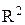= 0,9601
Вариация
выпуска продукции на 96,01% обусловлена вариацией объема
капиталовложений.
F = 120,38
Т.к., F > Fтабл., то с
вероятностью 0,95 уравнение регрессии статистически значимо.
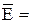2,24%
В среднем расчетные значения у(х)
отличаются от фактических значений на 2,24%.
3. Составим сводную таблицу вычислений
Таблица 1.1
|
Модель
|
Параметры
|
|
r (R)
|
|
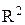
F
|
|
|
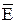
Линейная
|
0,9789
|
0,9582
|
114,59
|
2,24
|
|
Степенная
|
0,9787
|
0,9578
|
113,35
|
2,15
|
|
Показательная
|
0,9730
|
0,9467
|
88,81
|
2,40
|
|
Гиперболическая
|
0,9789
|
0,9601
|
120,38
|
2,24
|
В качестве лучшей модели для построения
прогноза выберем гиперболическую модель регрессии, т.к. она имеет большее
значение коэффициента детерминации о большее значение F- критерия Фишера.
4. Построим прогноз
а) точечный прогноз
хпр. = 1,1 *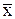 
= 1,1 * 62,29 = 68,519
млн. руб.
упр. = 153,90 –
4702/68,519 = 85,277 млн. руб.
б) интервальный прогноз
Верхняя граница прогноза: упр. + Uпр.
Нижняя
граница прогноза: упр. - Uпр.
Uпр. = Sу * tтабл. *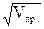 
Vпр. = 1 +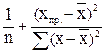 
Табличное значение t- критерия найдем с помощью функции СТЬЮДРАСПОБР (рис.
1.6).
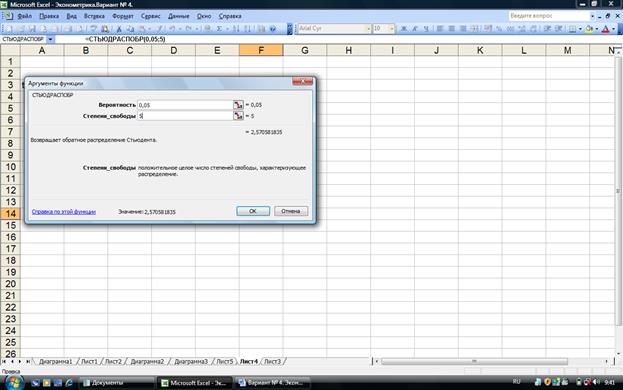
Рис. 1.6. Определение табличного значения t- критерия
Sу =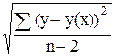 
Sу = 2,421
Vпр. = 1,2320
U(1) = 6,909
Результаты прогнозных оценок модели
регрессии представим в табл. 1.2.
Таблица 1.2
|
Таблица прогнозов ( р = 95% )
|
|
Значение фактора
|
Прогноз
|
Нижняя граница
|
Верхняя граница
|
|
68,519
|
85,277
|
78,368
|
92,186
|
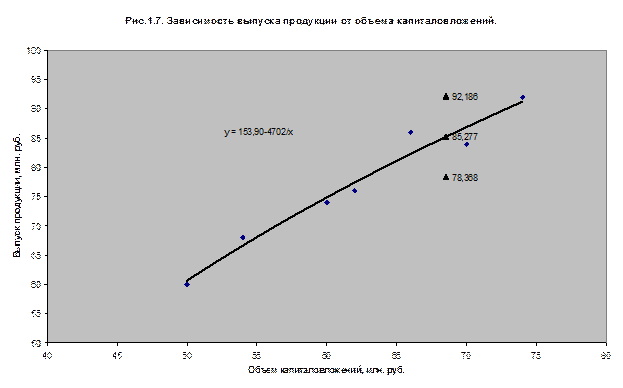
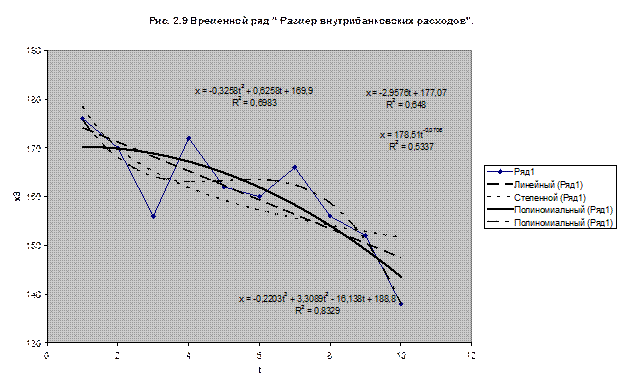
4. Отобразим на графике фактические данные
результаты расчетов и прогнозирования
Задача № 2
По десяти кредитным учреждениям получены
данные, характеризующие зависимость объема прибыли (У) от среднегодовой ставки
по кредитам (Х1), ставки по депозитам (Х2) и размера внутрибанковских расходов
(Х3):
|
У
|
60
|
68
|
80
|
76
|
44
|
96
|
100
|
104
|
106
|
98
|
|
Х1
|
50
|
54
|
60
|
62
|
70
|
54
|
84
|
82
|
86
|
84
|
|
Х2
|
22
|
30
|
20
|
32
|
44
|
34
|
52
|
56
|
66
|
68
|
|
Х3
|
176
|
170
|
156
|
172
|
162
|
160
|
166
|
156
|
152
|
138
|
Требуется:
1. Осуществить выбор факторных признаков
для построения двухфакторной регрессионной модели.
2. Рассчитать параметры модели.
3. Для характеристики модели определить:
-
линейный коэффициент множественной корреляции,
-
коэффициент детерминации,
-
средние коэффициенты эластичности,
- бета-, дельта-коэффициенты.
Дать
их интерпретацию.
4. Осуществить оценку надежности уравнения
регрессии.
5 Оценить с помощью t- критерия Стьюдента статистическую значимость
коэффициентов уравнения множественной регрессии.
6. Построить точечный и интервальный
прогнозы результирующего показателя.
7. Отобразить результаты расчетов на
графике.
Выполнение задач отобразить в аналитической
записке, приложить компьютерные распечатки расчетов.
Решение:
1. Осуществить выбор факторных признаков
для построения двухфакторной регрессионной модели
Рассчитаем матрицу коэффициентов парной
корреляции
Расчет параметров выполним с применением пакета прикладных
программ обработки электронных таблиц MS Excel в
среде Widows.
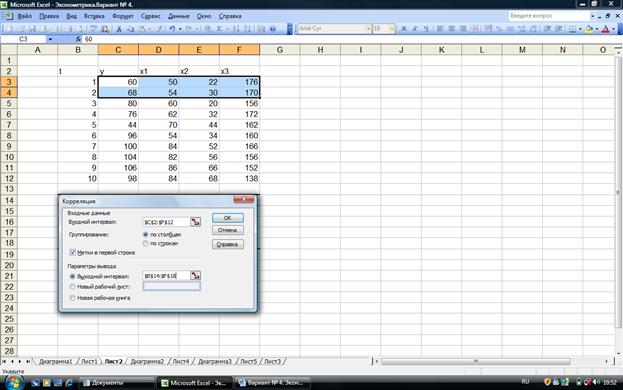
Рис. 2.1 Диалоговое окно Корреляция подготовлено к
выполнению анализа данных
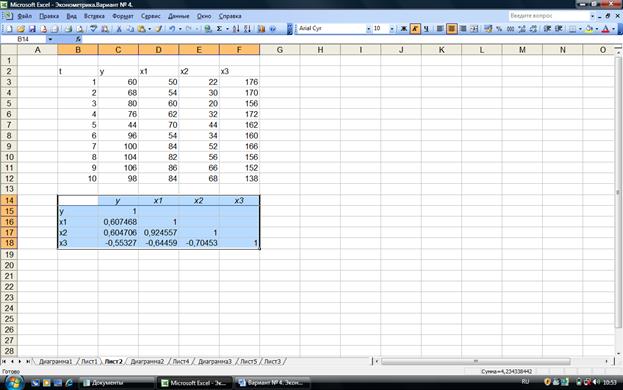
Рис. 2.2 Результат
корреляционного анализа
Анализ матрицы коэффициентов парной
корреляции показывает, что зависимая переменная, т.е. объем прибыли, имеет
тесную и прямую связь со среднегодовыми ставками по кредитам (rух1 = 0,6075), со ставками по депозитам (rух2 = 0,6047), и
тесную и обратную связь с размерами внутрибанковских расходов ( rух3 = - 0,5533).
Однако факторы Х1 и Х2 тесно связаны
между собой (rх2х3 = 0,9246), что свидетельствует о наличии
мультиколлинеарности. Из двух факторов
оставим в модели Х1.
2. Рассчитать параметры модели
У(х) = а0 + а1 * Х1 + а2 * Х3
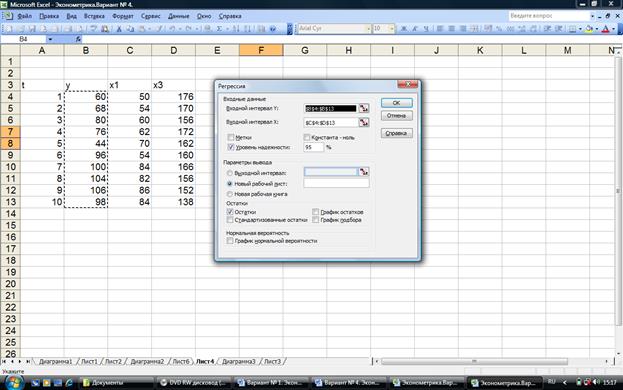
Рис. 2.3
Диалоговое окно Регрессия
подготовлено к
выполнению анализа данных
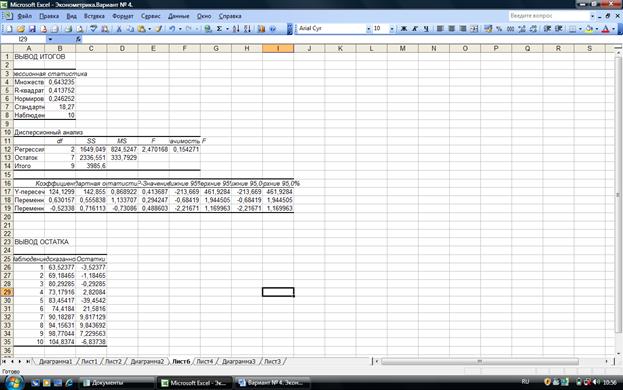
Рис. 2.4 Результат регрессионного анализа
Отсюда уравнение имеет вид:
У(х) = 124,130+ 0,630*Х1 – 0,523*Х3
3. Определим:
-
линейный коэффициент множественной корреляции
Согласно рис.2.4 имеем:
R = 0,6432
Связь между изучаемыми признаками тесная
- коэффициент детерминации
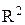= 0,4138
Вариация прибыли банка на 41,38%
обусловлена вариацией включенных факторов.
-
средние коэффициенты эластичности
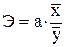
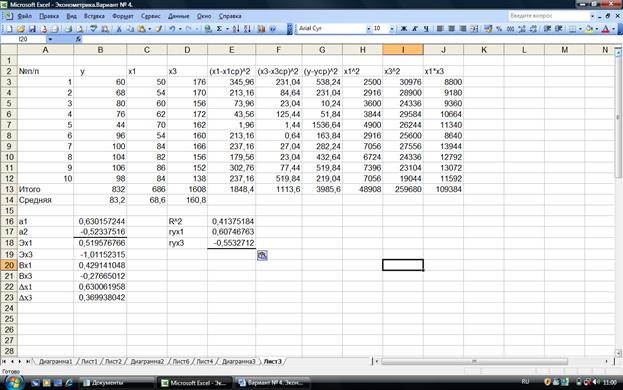
Рис. 2.5. Расчет средних коэффициентов эластичности,
β-коэффициентов и дельта коэффициентов
Эх1 = 0,5196%
Эх3 = - 1,0115%
Главным фактором изменения результативного
признака является фактор Х3, при его изменении на 1% прибыль банков снизится на
1,0115%.
- бетта- коэффициенты
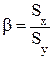
bx1 = 0,4291
bx3 = - 0,2767
C учетом
уровня колеблемости факторов наибольшие резервы в изменении результативного показателя
заложены в изменения фактора Х1.
- дельта коэффициенты
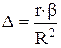
∆x1 = 0,63
∆x3 = 0,37
Наибольшая доля влияния выпадает на фактор
х1;
роль этого фактора в вариации результативного показателя составляет 63% общего
влияния двух факторов на результативный показатель.
4. Оценим значимость уравнения регрессии с
помощью F-критерия Фишера.
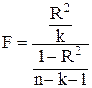
Согласно рис.2.4 имеем:
F = 2,47
Табличное значение F- критерия найдем с помощью функции FРАСПОБР
(рис. 2.6).
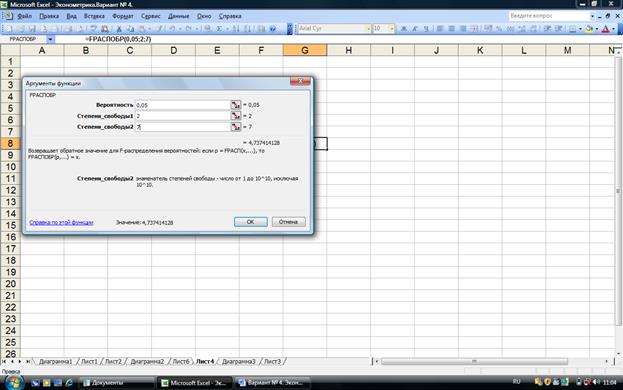
Рис. 2.6
Определение табличного значения F- критерия.
Т.к., F < Fтабл., то с вероятностью 0,95 уравнение регрессии
статистически не значимо.
5. Оценим значимость коэффициентов
уравнения регрессии с помощью t-критерия
Стьюдента
Согласно рис.2.4 имеем:
ta0 = 0,869
ta1 = 1,134
ta2 = - 0,731
Табличное значение t- критерия найдем с помощью функции СТЬЮДРАСПОБР (рис.
2.7).
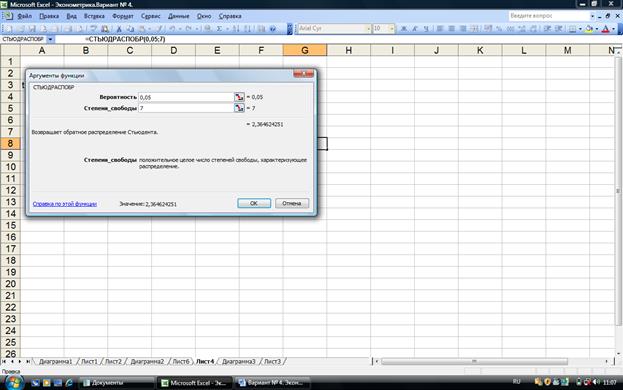
Рис. 2.7. Определение табличного значения t- критерия
С вероятностью 0,95 параметры а0, а1 и а2 статистически
незначимы, т.к. ta0 < tтабл., ta1< tтабл. и │ta2│ < tтабл.
6. Построим прогноз на 2 шага вперед
а) точечный прогноз
Построим точечные значения факторов на два
шага вперед используя следующие функции:
- линейную;
- степенную;
- полиноминальную 2-й степени;
- полиноминальную 3-й степени функции.
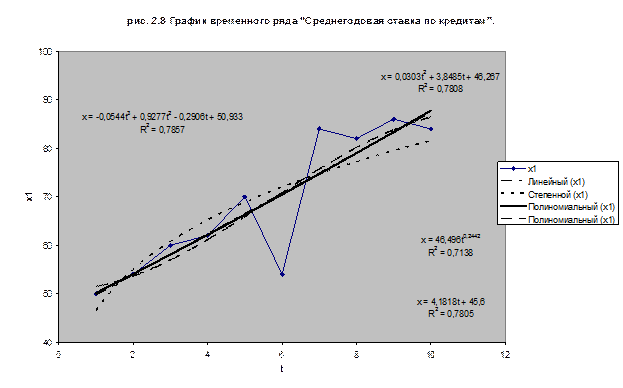
Для фактора Х1 выбрана полиноминальная модель
3-й степени, т.к. она имеет большее значение коэффициента детерминации
x1(t) = -0,0544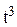
+ 0,9277
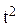- 0,2906t + 50,933
Для фактора Х2 выбрана полиноминальная модель
3-го порядка, т.к. она имеет большее значение коэффициента детерминации
X3(t) = -0,2203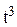 + 3,3089 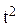- 16,138t + 188,8
Таблица 2.1
|
Упреждение
|
Прогноз
|
|
Х1
|
Х3
|
У
|
|
1
|
87,58
|
118,44
|
117,33
|
|
2
|
87,03
|
90,95
|
131,37
|
б) интервальный прогноз
Верхняя граница прогноза: Ур(n+k) + U(k).
Нижняя граница прогноза: Ур(n+k) - U(k).
U(k) = Sу * tтабл. *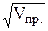 
Sу = 18,27
Vпр. =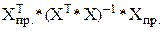 
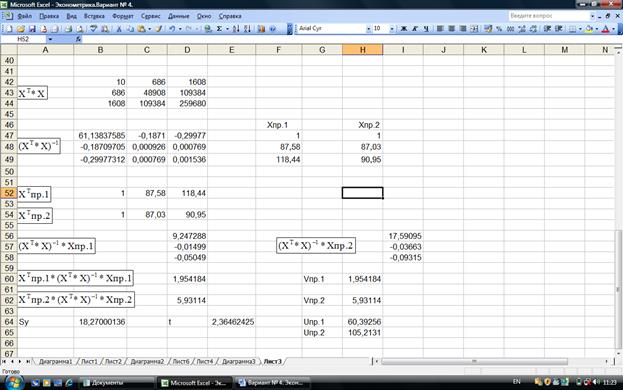
Рис. 2.10. Расчет интервального прогноза
U(1) = 60,39
U(2) = 105,21
Таблица 2.2
|
Таблица прогнозов (Р=95%)
|
|
Упреждение
|
Прогноз
|
Нижняя граница
|
Верхняя граница
|
|
1
|
117,33
|
56,94
|
177,72
|
|
2
|
131,37
|
26,16
|
236,58
|