1. Понятие модели и моделирования. Алгоритмы моделирования. Применение экономико-математического моделирования в маркетинговых исследованиях

Широкому использованию ЭММ и ЭВМ предшествовал длитель­ный период, в течение которого были решены такие проблемы, как математизация социальных явлений; создание кибернетических принципов управления; построение гибких вычислительных систем; освоение и серийное производство электронно-вычислительной тех­ники и др.

Еще в XVII веке выдающийся английский экономист Вильям Петти своим трудом «Политическая арифметика» положил начало этому процессу.                                            Существенный вклад в экономическую теорию и практику вне­сли советские ученые: балансовые методы планирования разра­батывались С.Г. Струмилиным, П.И. Поповым и др., модели эко­номического роста строил Г.А. Фельдман, методы линейного программирования разработал Л.В. Канторович, который впервые задачу хозяйственного планирования поставил и интерпретировал, как оптимизационную задачу [6].

В общении с природой, в процессе деятельности человек воспри­нимает окружающие его явления и формирует о них свое пред­ставление. Свои восприятия он отражает в виде описания, рисун­ка, результаты исследования, функции и связи явления -  в виде уравнений, формул.

Давно отмечено математическое сходство различных явлений.

Пример универсальности использования математического аппа­рата можно продемонстрировать на системе двух линейных алге­браических уравнений:

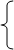a_iX_i+b_iX₂=C₁,

a₂X₁ + b₂X₂ = C₂.

Что означает это условие? Специалисты разных профилей мо­гут ответить, что это уравнение напряжений или силы тока в элек­трической цепи с активным сопротивлением, это может быть урав­нение загрузки станков; с помощью этого выражения могут быть сформулированы условия реализации товаров или осуществлен расчет рациона питания. Все засисит от того, что скрывается за постоянными коэффициентами а, в, С и символами неизвестных X₁ и X₂. Универсальность приведенной математической записи в том, что она отражает основные закономерности перечисленных яв­лений [6].

Математический аппарат позволяет имитировать поведение объ­екта в сложных, недоступных для эксперимента условиях, созда­вать и перебирать варианты построения дорогостоящих процессов без затрат трудовых и материальных ресурсов, выбирать наилуч­шие решения, «проигрывая» ситуации.

В частности, для эффективного управления надо изучить объект: установить его структуру, определить характеристику функ­ций, описать внутренние и внешние связи, исследовать законо­мерность поведения и т. п. Совокупность познаний, сведений об объекте необходимо представить в целостном образе, который дол­жен отражать его основные характеристики. В процессе изуче­ния объекта или отдельного явления устанавливают его свойства, взаимодействия и связи. Познанные свойства объекта (явления) необходимо описать, представить в форме, пригодной для иссле­дования [7].

Одной из распространенных форм описания является числовая, которая легко может быть переведена в алгебраическую форму. Это открывает широкие возможности для количественного анализа структуры и тенденций развития изучаемого процесса или объекта с использованием самых совершенных методов высшей математики.

Совокупность описанных свойств дает представление, условный образ процесса, объекта (системы). Этот условный образ, характеризующийся комплексом элементов, определенным образом вза­имосвязанных и отражающих функционирование и развитие дан­ного объекта (системы), понимается как модель.

Термин «модель» (перевод с латинского modulus) означает мера, образец, норма. В качестве модели можно рассматривать ма­кет дома или застройки жилого района, размещения оборудо­вания в торговом зале [6].

Модель может быть выполнена различными средствами. Напри­мер, можно представить форму объекта с помощью физической модели (макета), информационные связи характеризует информа­ционная модель, а функциональные связи, выраженные математи­ческим аппаратом, - математическая модель. Используемые в последнем случае символы (буквы и цифры) и их последователь­ности (формулы, уравнения и неравенства) описывают изучаемые свойства объекта и являются средством изображения модели.

Процесс разработки модели объекта или явления и исследова­ние познания объектов на их моделях называют моделированием.

Применение математических моделей для изучения экономиче­ских закономерностей называют экономико-математическим моде­лированием, а использование таких моделей в практике управле­ния - экономико-математическими методами управления [5].

Анализ сложившейся практики моделирования различных про­цессов в экономике показывает некоторую типичность алгоритмов моделирования. Последовательность действий моделирования соответствует тезису материалистической философии: от живого созер­цания к абстрактному. Отображение изучаемого явления, процесса, системы как совокупности определяющих их элементов, сущест­венных с точки зрения поставленной цели, и взаимосвязей между ними должно быть подобно изучаемому объекту. Результатом этой работы является создание условного образа, которому дол­жна соответствовать модель. Алгоритм построения модели можно представить в такой последовательности:

1. Постановка цели.

1.1. Сбор и анализ информации.   

1.2. Формирование целей и критериев.

2. Построение модели.

2.1. Выбор средств имитации.

2.2. Конструирование модели.

2.3. Проведение экспериментальных расчетов.

2.4. Проверка модели на адекватность [6].

Ниже приводится краткая характеристика перечисленных эта­пов.

Постановка цели занимает особое место в моделировании. Чет­ко поставленная цель определяет состав и количественную харак­теристику основных элементов системы и их взаимосвязи.

Начальным этапом моделирования являются сбор и анализ ин­формации. От правильного подбора данных для анализа зависит конечный результат моделирования. Собранные данные должны быть выражены в абсолютных величинах и единых единицах изме­рения, отличаться сопоставимостью и отражать типичные черты изучаемой совокупности. Выбранная единица измерения должна отвечать следующим условиям: обеспечивать пересчет данных пер­вичных документов в условные единицы; не зависеть от построения логических структур и технических решений средств сбора, пере­дачи и обработки информации; давать возможность сопоставлять получаемые результаты.

Информационные потоки независимо от содержания характери­зуются источником возникновения, направленностью, периодично­стью, частотой, степенью взаимосвязи и постоянства, информа­ционной емкостью отдельных сообщений, способом индикации, объемом и плотностью потока, видом носителя информации и т. п. [7].

Анализ информации состоит из двух этапов: на первом осу­ществляют упорядочение и отбор данных, на втором этапе на базе отобранных данных изучают объект, явление. Существенное место при этом занимает прагматический анализ информации, в резуль­тате которого выявляют ценность данных с точки зрения пользо­вателя. Здесь важно из массы данных отобрать минимальную, но достаточную информацию для принятия эффективного управлен­ческого решения [1].

Созданная информационная база должна удовлетворять сле­дующим требованиям: отвечать потребности пользователя в данных для реализации функций управления, адекватно отражать объект управления в любой момент времени, обеспечивать сопоставимость результатов решения задач и показателей между сопрягающими моделями, содержать интересующие нас характеристики объекта исследования, отражать закономерности его развития. Процесс, создания информационной базы носит итеративный характер.    

На втором этапе анализа информации изучают объект. Причем наши познания о нем представляются, как правило, в виде сложной системы. Его структуру определяют путем декомпозиции системы на локальные подсистемы, выявляют функции управления, внут­ренние и внешние информационные и функциональные связи, уста­навливают количественные характеристики. Ввиду сложности экономических процессов в любой модели учитывают лишь те факторы, которые отражают интересующие нас типичные явления. Рост числа учтенных факторов приближает ее к реальной действительности, но при этом чрезвычайно усложняет.                

Чтобы можно было работать с моделью, она должна быть до­ступной для математического изучения. Это обеспечивается под­бором соответствующих факторов, правильной формулировкой целей, тщательным выбором критериев. На этом заканчивается подготовительный этап моделирования, на котором формируется все необходимое для построения модели [4].

При построении модели необходимо соблюдать следующие требования: адресность к определенному управленческому исполнителю, отсутствие логического противоречия, учет всех важнейших элементов задачи принятия решения, адаптацию к реальным условиям, доступность в эксплуатации.                             

Исходным моментом построения модели является выбор средств имитации - математического аппарата, формирующего условный образ объекта. Разнообразная практика использования математических методов в экономике дает широкие возможности творческого поиска в этой сфере. Так, методы оптимального про­граммирования эффективно используются для составления планов товарооборота и его структуры, рационов питания в общественном питании, для решения различных транспортных задач. Модели, построенные с использованием теории игр, применяются для решения альтернативных задач (размещение оборудования при нали­чии ограниченных площадей, организация продажи новых товаров и т.д.). Системы массового обслуживания используются при обслуживании большого количества покупателей, для расчета тех­нологических процессов движения товаров. Методы сетевого планирования и управления дают хорошие результаты при построении моделей больших торговых центров, создании и освоении АСУ в торговле, проведении ярмарок. Данный перечень не охватывает всех примеров применения математических методов в экономике, но он показывает необходимость проведения анализа при использовании математического аппарата в каждом конкретном случае [6].

На основе проведенного анализа и выбранных математических методов осуществляется конструирование модели - отображение условного образа объекта. На базе построенной мо­дели осуществляется серия экспериментальных расчетов с учетом возможных вариантов конкретной ситуации. Накоплен­ная в результате экспериментов информация используется для про­верки модели на адекватность.

Даже самая хорошая модель отражает только общие закономерности и, кроме того, моделируемые про­цессы, как правило, отличаются разнообразием описания. Ввиду сложности этих процессов каждая модель описывает лишь опре­деленный аспект.

Различные модели одного и того же явления или взаимосвязан­ных явлений дополняют друг друга. Это открывает перспективу це­лостного моделирования торговых процессов, функционирования торговых объектов. Следовательно, при определении адекватности моделей реальному объекту необходим тщательный подбор методов идентификации модели. В этих целях осуществляется сравнение результатов экспериментов с моделью и фактическими данными. Если полученные результаты способствуют достижению поставлен­ной цели, то разработанная модель используется в практической деятельности. Если результаты не удовлетворяют этим условиям, проводится корректировка модели с последующей серией экспери­ментальных расчетов [6; 7].

Экономико-математическое моделирование в маркетинговых исследованиях чаще всего связывают с изучением спроса населения, которое включает в себя следующие основные этапы:

- выбор показателя спроса населения;

- сбор исходной статистической информации, ее систематизацию и оценку;

- отбор существенных факторов, которые необходимо учитывать при построении моделей изучения и прогнозирования спроса;

- построение диаграмм рассеивания, подбор математических форм связи между величиной спроса и влияющими на него факторами;

- расчет параметров и построение экономико-математической мо­дели изучения или прогнозирования спроса;

- оценку полученной модели математико-статистическими мето­дами;

- проведение вычислений по модели;

- экономическую интерпретацию модели и разработку рекомен­даций по ее применению в торговле [2; 3; 6].

Исходным показателем спроса может быть, например, размер спроса населения на отдельные товары в стоимостном выражении или его удельный вес в общем объеме платежеспособного спроса населения на все товары; размер спроса на отдельные продоволь­ственные товары в натуральных единицах измерения, приобретен­ные в государственной и кооперативной торговой сети, на колхоз­ном рынке; размер спроса на отдельные продукты питания с учетом всех источников поступления; уровень фактической обеспеченно­сти населения отдельными видами товаров длительного пользова­ния, исчисляемый в расчете на 1000 человек населения или 100 се­мей, и т. д.

Спрос населения находится под воздействием множества факто­ров. Причем в экономико-математическую модель можно включать только количественно измеряемые факторы и, кроме того, не все, а наиболее существенные. Такими факторами, например, являются: денежные доходы населения, розничные цены товаров, размер и состав семьи, число семей. Кроме них, необходимо выде­лить группу специфических факторов формирования спроса на конкретный товар. В этом случае проводят детальный анализ и определяют степень влияния отдельных факторов, например посред­ством коэффициента корреляции, коэффициента эластичности спро­са, параметров уравнения регрессии. Сокращение числа факторов можно проводить путем их агрегирования.

Факторы принято разделять на экзогенные, т.е. внешние по отношению к моделируемому объекту, и эндогенные, т.е. внутренне присущие моделируемому процессу.

К экзогенным относится практически вся совокупность воздей­ствующих на спрос факторов. К эндогенным относится общая тен­денция развития спроса на конкретный товар. В модель эндоген­ный фактор вводится в виде специального фактора-тренда t [6].

Выделяют также факторы, влияние которых на величину спроса количественно не измеряется (национальные особенности, тради­ции, обычаи, мода и др.), и факторы, количественно измеряемые [1].

Поскольку на спрос влияет большое количество факторов, зада­чу моделирования приходится упрощать путем выделения несущест­венных и существенных факторов, последние из которых и вклю­чают в модель.

Для моделирования спроса населения применяются методы и модели корреляционно-регресивного анализа. При этом экономико-математические модели спроса строятся в виде уравнений регрессии – одно- или многофакторных, в которых в качестве независимых переменных выступают формирующие спрос факторы, а в качестве зависимой переменной – спрос наслеления.

2. Формальные и неформальные методы прогнозирования

Проблема прогнозирования, вследствие быстрых, порой плохо предсказуемых изменений внешней среды, за последнее десятилетие ста­ла особенно сложной. С учетом этих трудностей и критичности ошибок в прогнозах некоторые специалисты были вынуждены заговорить о тщет­ности прогнозирования. На самом деле прогнозирование - это обязан­ность, которую в явной или неявной форме неизбежно должны выпол­нять все фирмы [2].

Помимо получения возможных будущих оценок тех или иных исследуемых параметров, целью прогнозирования также является побужде­ние к размышлению о том, что может произойти во внешней среде и к каким последствиям для фирмы это приведет. Прогнозирование повыша­ет бдительность менеджеров и, следовательно, их способность реагиро­вать на изменения. Этот эффект достигается даже тогда, когда план не ­выполнен в связи с тем, что некоторые гипотезы, положенные в основу прогнозного сценария, не материализовались.

Методы прогнозирования, как и все методы, используемые при проведении маркетинговых исследований, можно классифицировать на эвристические (неформальные), при применении которых преобладают субъективные на­чала, и на экономико-математические (формальные), при применении которых преоб­ладают объективные начала, к числу которых относятся статистические методы [3].

Эвристические методы предполагают, что подходы, используемые для формирования прогноза, не изложены в явной форме и неотделимы от лица, делающего прогноз, при разработке которого доминируют ин­туиция, прежний опыт, творчество и воображение. К данной категории методов относятся методы социологических исследований и экспертные методы, рассмотренные ранее. Причем опрашиваемые, давая свои оцен­ки, могут основывать свои суждения как на голой интуиции, так и ис­пользуя определенные причинно-следственные связи, данные статистики и расчетов.

Так, при прогнозировании спроса изучаются предпочтения потре­бителей; в качестве экспертов может рассматриваться торговый персонал, обслуживающий определенные территории, дилеры, дистрибьюторы, консультанты по маркетингу и т.д.

При использовании экономико-математических методов подходы к прогнозированию четко сформулированы и могут быть воспроизведены другими лицами, которые неизбежно придут к получению такого же прогноза.

Если при применении экспертных методов структура причинно-следственных связей, используемая разными экспертами, может быть различной, то при использовании экономико-математических методов структура моделей устанавливается и проверяется экспериментально, в условиях, поддающихся объективному наблюдению и измерению [2].

Определение системы факторов и причинно-следственной (казуа­льной) структуры исследуемого явления - исходная точка экономико-математического моделирования.

Каждый из рассмотренных возможных методов прогнозирования обладает определенными достоинствами и недостатками. Их применение более эффективно в краткосрочном прогнозировании. Они сильно упро­щают реальные процессы, чтобы можно было рассчитывать на получение с их помощью результатов, выходящих за рамки представлений сего­дняшнего дня. Практически невозможно отразить в моделях долгосроч­ного прогнозирования структурные сдвиги, постоянно происходящие в изменяющемся мире.

На самом деле все эти методы являются взаимодополняющими. Эффективная прогнозная система должна обеспечивать возможность использования любого из этих методов.

Примером сложной задачи прогнозирования, которая не решается с помощью какого-то одного метода, является прогнозирование объема продаж нового товара. При проведении маркетинговых исследований оцениваются объемы продаж нового товара в течение первых лет (ска­жем, трех) после выпуска. Для этой цели могут быть применены эксперт­ные методы, методы опросов, проведение продаж на контрольном рынке [2; 3].

Экспертные оценки, сформулированные специалистами по марке­тингу, базируются на сведениях, собранных на стадии предварительного анализа и учитывающих данные о продажах конкурентов, размере потен­циального рынка, общем спросе, долях продуктов различных марок на рынке, доступности сбытовых сетей и др.

Недостающая информация собирается путем прямых опросов потенциальных пользователей, торговцев, поставщиков и, если это возмож­но, конкурентов.

Проверка рынка, или контрольная продажа, в ходе которой наблю­дается реальное рыночное поведение покупателей, позволяет оценить уровень пробных и повторных закупок и объем потенциальных продаж нового товара. Можно также провести пробные продажи по месту жи­тельства или эксперименты в специальных лабораториях-магазинах.

Данные методы обычно применяются совместно. Используя любой из перечисленных или какой-либо иной подход, служба маркетинга должна установить перспективный объем продаж нового товара, на осно­ве которого разрабатываются стратегии запуска товара [2].

Ясно, что в условиях турбулентной внешней среды интуиция и воображение способны стать важными инструментами восприятия реально­сти, дополняя количественные подходы, которые, по определению, опи­раются только на наблюдаемые факторы. С другой стороны, понятно, что чисто качественному методу также присущи значительные погрешности и что интуиция должна в возможно большей степени проверяться с помо­щью доступных фактов и знаний. Таким образом, следует обеспечить совместное использование этих двух подходов.

Метод сценариев - это хорошее средство для организации взаимодействия количественного и качественного подходов, для интегрирования рассмотренных прогнозных методов. Сценарий - это динамическая мо­дель будущего, в которой шаг за шагом описывается возможный ход со­бытий с указанием вероятностей их реализации. В сценарии представля­ются ключевые причинные факторы, которые должны быть приняты во внимание, и указываются способы, которыми эти факторы могут повли­ять, скажем, на первичный спрос [2].

Обычно составляется несколько альтернативных вариантов сцена­рия, реализация которых возможна при различных допущениях (о поли­тической, правовой и экономической обстановке, о положении в данной отрасли, о новых возможностях и проблемах данной фирмы и т.п.). Сле­довательно, сценарий - это характеристика будущего в духе изыскатель­ского прогнозирования, а не определение одного желательного состояния или «точечная оценка» того, что произойдет в будущем.

Один, наиболее вероятный, вариант сценария обычно рассматри­вается в качестве базового, на основе которого принимаются текущие решения. Другие, рассматриваемые в качестве альтернативных, «запуска­ются» в реализацию в том случае, если реальность в большей мере начи­нает соответствовать их содержанию, а не базовому варианту сценария.

Написание сценариев обычно совершается в явно выраженных временных координатах. Вначале метод написания сценариев использо­вался для выявления возможных военных и дипломатических кризисов. Затем он стал применяться в стратегическом корпоративном планирова­нии, а потом и как интеграционный механизм прогнозирования отдель­ных социально-экономических процессов, в том числе рыночных [2; 3].

Сценарии являются одним из наиболее эффективных средств ос­лабления традиционного мышления; сценарий заставляет «погрузиться» в незнакомый и быстро меняющийся мир настоящего и будущего, раскры­вая возможности, в которых фокусируется его развитие.

Сценарий заставляет исследователя заниматься деталями и процес­сами, которые он мог бы легко упустить, изолированно используя от­дельные методы прогнозирования.

Сценарий, следовательно, отличается от прогноза. Прогноз - это суждение, которое стремится «предсказать» специфическую ситуацию и должно быть принято или отвергнуто на базе его достоинств и недостат­ков [1]. Сценарий же является инструментом, который используется для оп­ределения, какие виды прогнозов должны быть разработаны, чтобы буду­щая ситуация была описана полно, с учетом всех главных факторов.

Сценарий заставляет размышлять и обеспечивает:

- лучшее понимание рыночной ситуации и ее эволюции в про­шлом, настоящем и будущем;

- оценку потенциальных угроз для фирмы;

- выявление благоприятных возможностей для фирмы;

- выявление возможных, наиболее целесообразных направлений деятельности фирмы;

- повышение уровня адаптированности фирмы к изменениям внешней среды [2].

Таким образом, метод сценариев позволяет повысить способность к предвидению и развить гибкость и адаптивность фирмы к переменам. Этот метод, который исходит из убеждения о том, что будущее никогда не может быть полностью измерено и управляемо, обладает, с точки зре­ния управления, рядом важных достоинств:

1. Прежде всего, он заостряет внимание фирмы на неопределенно­сти, которая характеризует любую рыночную ситуацию: управление в турбулентной среде подразумевает способность предвидеть эволюция этой среды.

2. Метод сценариев облегчает интеграцию данных, полученных разными методами, качественными или количественными.

3. Реализация этого метода вносит в управление дополнительную гибкость и способствует разработке альтернативных планов и системы быстрого реагирования на изменения внешней среды [2; 3].

Наиболее широко в прогнозировании, как и в целом при проведе­нии маркетинговых исследований, из математических методов использу­ются статистические методы.

3. Применение сетевого планирования в управлении товародвижением

Разнообразие и взаимозависимость задач, решаемых в области планирования и управления торговлей, требуют научно обосно­ванной системы планового руководства и действенного контроля за ходом выполнения работ. Для этой цели используют такой эффективный инструмент, как сетевые методы и модели, на базе которых создаются системы сетевого планирова­ния и управления (СПУ). Эти системы предназначены для управ­ления сложными объектами, получившими название комплексов взаимосвязанных работ, операций, тем, разработок, требующих четкой координации действий множества исполнителей. СПУ позво­ляют осуществлять надежную координацию всех звеньев и подраз­делений, участвующих в комплексе, и выполнять большой объем работ с высокой вероятностью соблюдения заданных сроков.

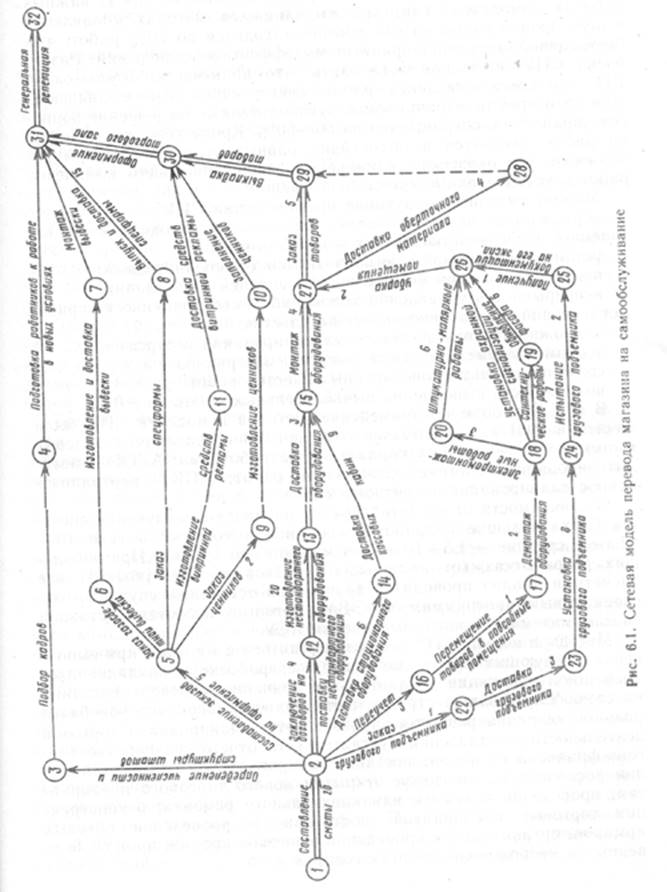
Здесь используется информационно-динамическая модель осо­бого вида (так называемая сетевая модель) для логико-математи­ческого описания и алгоритмизации расчетов параметров этого процесса (продолжительности, трудоемкости, стоимости и т. д.) гра­фическими и аналитическими методами.

В СПУ применяется графическое изображение (Рисунок 1) или аналитическая запись плана работ, в которой отражаются их логическая последовательность, взаимосвязь и продолжительность. Они выполняются с целью оптимизации разработанного плана и текущего управления ходом работ путем периодического сбора информации и соответствующей корректировки плана [6].

Системы СПУ являются комплексом графических и расчетных методов, организационных мероприятий и контрольных приемов, обеспечивающих моделирование и оперативную корректировку планов в торговле. Причем графические методы дают наиболее наглядную информацию о ходе работ как в целом,    так    и    в деталях. В целом система СПУ включает сбор, переработку

информации, поступающей от управляемого объекта, выработку решений на ее основе и передачу распоряжений на управляемый объект.

СПУ концентрируют внимание руководителей на самых важных работах комплекса. Так, при сложившихся методах управления в поле зрения руководителя обычно находится до 70% работ, что, безусловно, затрудняет принятие им эффективных решений. Разра­ботка СПУ позволила установить, что практически лишь около 10% из всего комплекса работ имеют существенное значение. При этом время, затрачиваемое руководителями на решение вопро­сов управления, сокращается на 50-60%. Кроме того, все участни­ки работ находятся в объективно равных условиях информиро­ванности, что оказывает влияние на завершение всего комплекса работ в установленные сроки.

Можно выделить следующие преимущества СПУ:

- возможность концентрировать внимание руководителя на не­большом числе участков работ и исполнителей;

- установление четкой взаимосвязи между исполнителями;

- получение в любой момент исчерпывающей информации;

- непрерывность управления ходом работ, своевременность приня­тия решений, оперативность вмешательства;

- возможность рационального маневрирования ресурсами;

- экономия времени, средств, энергии, материалов и т. д.;

- создание объективной картины качества работ;

- возможность выполнения вычислительных работ на ЭВМ [6].

В зависимости от масштаба работ различают следующие систе­мы СПУ: большие разработки - с числом событий в сети 10-12 тыс., средние - 1,5-10 тыс. и малые - до 1,5 тыс. При неболь­ших разработках (от нескольких десятков до ста событий) все расчеты и анализ проводятся вручную, в остальных случаях - по специальным программам на ЭВМ, которые являются составной частью математического обеспечения АСУ [6; 7].

Методы и модели СПУ могут применяться в торговле при выпол­нении следующих работ: заготовке, переработке и закладке продукции на длительное хранение; переводе магазина на самообслуживание; строительстве универсальной оптовой базы; разработке плана развития торговой сети; планировании торговой деятельности; составлении бухгалтерского отчета; разработке торгово-финансового плана; поставке товаров покупателям; заключе­нии договоров на поставку; открытии нового торгового предприя­тия; проведении текущего или капитального ремонта; реконструк­ции торговых предприятий; подготовке и проведении оптовых ярмарок, организации и проведении выставок-продаж продовольст­венных и непродовольственных товаров.

Список литературы

1. Акофф Р., Сасиени М. Основы исследования операций. – М.:Мир,1971.-238с.

2. Голубков Е.П. Маркетинговые исследования: теория, методология и практика. – М.:Финпресс,1998.-416с.

3. Голубков Е.П. Маркетинг: стратегии, планы, структуры. – М.:Дело,1995.-347с.

4. Ковалев А.И., Войленко В.В. Маркетинговый анализ. – М.:Центр экономики и маркетинга,1996.-367с.

5. Математические методы в планировании отраслей и предприятий/Под ред. А.Я. Боярского. – М.:Изд-во МГУ,1983.-288с.

6. Спирин А.А., Фомин Г.П. Экономико-математические методы и модели в торговле. – М.:Экономика,1988.-149с.

7. Щедрин Н.И., Кархов А.Н. Экономико-математические методы в торговле. – М.:Экономика,1980.-346с.