ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-
ЭКОНОМИЧЕСКИЙ
ИНСТИТУТ
Филиал в г. Омске
Кафедра автоматизированной обработки
экономической информации
КОНТРОЛЬНАЯ РАБОТА
По
дисциплине « Информационные системы в экономике»
Вариант
№ 5
Выполнила: студентка 3 курса
2 потока, 7 группы;
Факультет: ФиК (утро)
Инд. №: 05ФФБ00495
Семенова Александр Николаевна
Проверил: Забудский Г. Г.
СОДЕРЖАНИЕ:
1)Задача по теме «ОПРЕДЕЛЕНИЕ
РЫНОЧНОЙ
СТОИМОСТИ ОБЛИГАЦИИ» ……………………………………………2 стр.
2)Задача по теме «РАСПРЕДЕЛЕНИЕ
ИНВЕСТИЦИЙ»……………. 4 стр.
ОПРЕДЕЛЕНИЕ РЫНОЧНОЙ СТОИМОСТИ
ОБЛИГАЦИИ
ПОСТАНОВКА
ЗАДАЧИ
Известен номинал облигации, процент ежегодных
доходов (процент на купоне) и срок действия облигации. Кроме того, известны
банковская ставка в момент выпуска облигации и момент времени, когда банковская
ставка изменяется и до какой величины.
Задание.
1.
Определить
рыночную стоимость облигации в течении всего периода ее действия.
2.
Построить
график изменения рыночной стоимости.
3.
Кратко
описать действия в EXCEL.
|
Номинал облигации
|
Процент на купоне
|
Срок погашения
|
Банковская ставка в момент выпуска
|
Год изменения банковской ставки
|
Новая банковская ставка
|
|
4000
|
8
|
10
|
6
|
5
|
12
|
Решение:
Стоимость
облигации в момент времени t=0,1,2,…,n рассчитывается
по формуле:
CO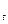
=(Y (1-(1+j)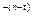
))/j +
S/(1+j)
,
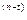CO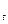- стоимость облигации в момент времени t;
j- банковская ставка (десятичная дробь);
t-
момент времени: 0-момент выпуска, 1 – через год после выпуска и т.д.;
n-
срок действия облигации (кол-во лет);
S – номинал облигации;
Y-
ежегодный доход, определяется по проценту на купоне.
Используя Excel
можно формулу вычисления стоимости разложить на составляющие, например,
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
H
|
I
|
J
|
|
t
|
n-A
|
j
|
1+C
|
D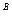
|
1/E
|
(1-F)/C
|
Y*G
|
S/E
|
H+I
|
В
верхней строке указанной таблицы обозначения столбцов в Excel. Во второй строке показаны формулы, которые должны
быть записаны в ячейки. Здесь A, B, C,
D, E,
F, G,
H, I это адреса ячеек.
Тогда,
например, в столбце E
вычисляется формула (1+j)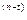, в столбце F: (1+j)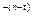 и т. д. Здесь используется свойство Excel автоматической смены адресации строк при “движении”
по столбцу.
|
t
|
n-A
|
j
|
1+C
|
D^B
|
1/E
|
(1-F)/C
|
Y*G
|
S/E
|
H+I
|
|
1
|
9
|
0,06
|
1,06
|
1,689479
|
0,591898
|
6,801692
|
2176,542
|
2367,594
|
4544,135
|
|
2
|
8
|
0,06
|
1,06
|
1,593848
|
0,627412
|
6,209794
|
1987,134
|
2509,649
|
4496,784
|
|
3
|
7
|
0,06
|
1,06
|
1,50363
|
0,665057
|
5,582381
|
1786,362
|
2660,228
|
4446,591
|
|
4
|
6
|
0,06
|
1,06
|
1,418519
|
0,704961
|
4,917324
|
1573,544
|
2819,842
|
4393,386
|
|
5
|
5
|
0,12
|
1,12
|
1,762342
|
0,567427
|
3,604776
|
1153,528
|
2269,707
|
3423,236
|
|
6
|
4
|
0,12
|
1,12
|
1,573519
|
0,635518
|
3,037349
|
971,9518
|
2542,072
|
3514,024
|
|
7
|
3
|
0,12
|
1,12
|
1,404928
|
0,71178
|
2,401831
|
768,586
|
2847,121
|
3615,707
|
|
8
|
2
|
0,12
|
1,12
|
1,2544
|
0,797194
|
1,690051
|
540,8163
|
3188,776
|
3729,592
|
|
9
|
1
|
0,12
|
1,12
|
1,12
|
0,892857
|
0,892857
|
285,7143
|
3571,429
|
3857,143
|
|
10
|
0
|
0,12
|
1,12
|
1
|
1
|
0
|
0
|
4000
|
4000
|
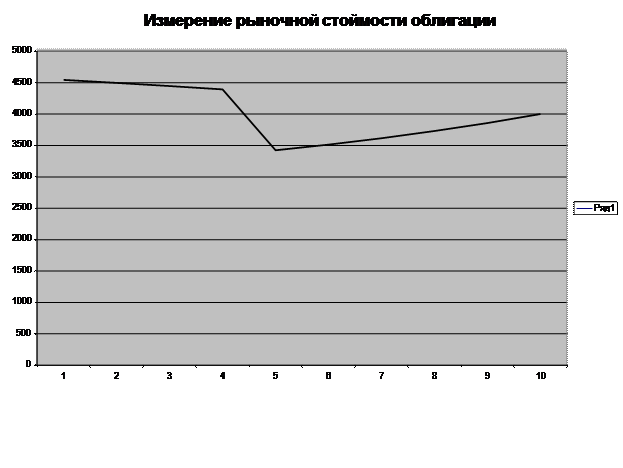
В
столбце J будет определена рыночная стоимость облигации
по годам с момента выпуска. График строится стандартным образом с помощью
МАСТЕР ДИАГРАММ.
РАСПРЕДЕЛЕНИЕ ИНВЕСТИЦИЙ
ПОСТАНОВКА ЗАДАЧИ.
Денежные средства могут быть использованы для финансирования 2-х
проектов А и В. Период инвестиций в проект А
кратен 1 году , а в проект В – 2
годам . Известно сколько гарантирует прибыли на вложенный рубль каждый проект
(данные в таблице). Как следует распорядиться заданным капиталом, чтобы через 4
года капитал был максимальным?
Задание.
1. Составить модель линейного программирования.
2. Используя
средство «ПОИСК РЕШЕНИЯ» в «EXCEL» найти оптимальный план распределение капитала по
проектам.
3. Найти границы эффективности проектов, при которых
вложения в проект А меняется на вложения в проект В и наоборот.
4. Кратко описать действия в EXCEL.
|
Величина капитала (руб.)
|
Прибыль по проекту А (коп. на 1 руб.)
|
Прибыль по проекту В (коп. на 1 руб.)
|
|
15000
|
25
|
65
|
Составляем
модель линейного программирования
1,25*X4A +1,65*X3B ---à MAX целевая функция
X1A + X1B<= 1000
ограничение на начало 1 года
X2A+X2B<=1,25*X1A ограничение на начало 2 года
X3A+X3B<=1,25*X2A + 1,65*X1B ограничение на начало 3 года
X4A+X4B<=1,25*X3A+ 1,65*X2B ограничение на начало 4 года
Для
записи ограничений и целевой функции необходимо
в ограничениях переменные перенести в левую часть, меняя знак на
противоположный.
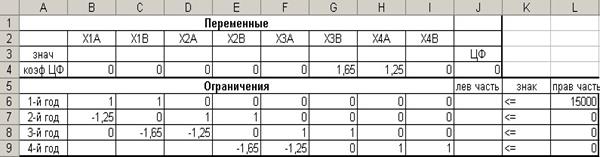
В
ячейке J4 формула: СУММПРОИЗВ(B$3:I$3;B4:I4)
В
ячейке J6 формула:
СУММПРОИЗВ(B$3:I$3;B6:I6)
В
ячейке J7 формула:
СУММПРОИЗВ(B$3:I$3;B7:I7)
В
ячейке J8 формула:
СУММПРОИЗВ(B$3:I$3;B8:I8)
В
ячейке J9 формула:
СУММПРОИЗВ(B$3:I$3;B9:I9)
После
заполнения таблицы данных вызывается «СЕРВИС»
-> «ПОИСК РЕШЕНИЯ»
В
поле «установить целевую ячейку»
внести адрес «$J$4»
В
поле «изменяя ячейки» внести адреса «B$3:I$3»
Курсор в поле «добавить». Появится диалоговое окно «Добавление ограничения»
В поле «ссылка на ячейку» ввести адрес «$J$6»
Курсор в правое
окно «ограничение» и ввести адрес «$L$6»
На
кнопку «добавить». На экране опять
диалоговое окно «Добавление ограничения»
и аналогично ввести другие ограничения. После ввода последнего ограничения
ввести ОК.
После ввода
последнего ограничения в окне «Ограничения» появятся неравенства, показывающие,
что левая часть неравенств меньше либо равна правой части, т.е.
$J$6 <= $L$6
$J$7 <= $L$7
$J$8 <= $L$8
$J$9 <= $L$9
Нажимаем
на кнопку «Параметры» и щелкаем
левой клавишей мыши в окнах «Линейная
модель» и «Неотрицательные значения»
затем кнопку
“ОК” из окна “Параметры поиска
решения” переходим в окно “Поиск
решения” и щелкаем левой клавишей
мыши на “Выполнить” и на экране окно
“Результаты поиска решения”
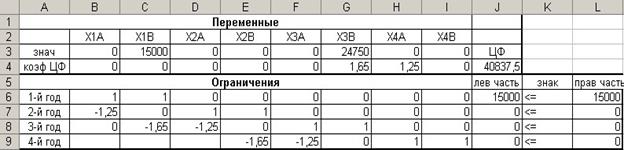
Отчёт по
результатам
|
Целевая
ячейка (Максимум)
|
|
|
|
|
Ячейка
|
Имя
|
Исходное
значение
|
Результат
|
|
|
$J$4
|
коэф
ЦФ ЦФ
|
40837,5
|
40837,5
|
|
Изменяемые
ячейки
|
|
|
|
|
Ячейка
|
Имя
|
Исходное
значение
|
Результат
|
|
|
$B$3
|
знач
Х1А
|
0
|
0
|
|
|
$C$3
|
знач
Х1В
|
15000
|
15000
|
|
|
$D$3
|
знач
Х2А
|
0
|
0
|
|
|
$E$3
|
знач
Х2В
|
0
|
0
|
|
|
$F$3
|
знач
Х3А
|
0
|
0
|
|
|
$G$3
|
знач
Х3В
|
24750
|
24750
|
|
|
$H$3
|
знач
Х4А
|
0
|
0
|
|
|
$I$3
|
знач
Х4В
|
0
|
0
|
|
Ограничения
|
|
|
|
|
|
|
Ячейка
|
Имя
|
Значение
|
Формула
|
Статус
|
Разница
|
|
|
$J$6
|
1-й
год лев часть
|
15000
|
$J$6<=$L$6
|
связанное
|
0
|
|
|
$J$7
|
2-й
год лев часть
|
0
|
$J$7<=$L$7
|
связанное
|
0
|
|
|
$J$8
|
3-й
год лев часть
|
0
|
$J$8<=$L$8
|
связанное
|
0
|
|
|
$J$9
|
4-й
год лев часть
|
0
|
$J$9<=$L$9
|
связанное
|
0
|
Чтобы найти границы эффективности проектов, при
которых вложения в проект В меняется на вложения в проект А и наоборот увеличиваем прибыль от проекта А
на 4 коп.
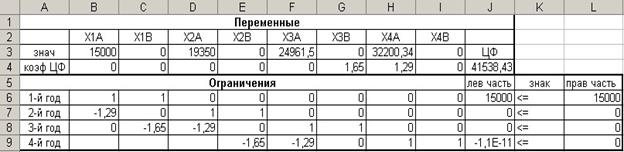
Отчёт по
результатам
|
Целевая
ячейка (Максимум)
|
|
|
|
|
Ячейка
|
Имя
|
Исходное
значение
|
Результат
|
|
|
$J$4
|
коэф
ЦФ ЦФ
|
41538,43215
|
41538,43215
|
|
Изменяемые
ячейки
|
|
|
|
|
Ячейка
|
Имя
|
Исходное
значение
|
Результат
|
|
|
$B$3
|
знач
Х1А
|
15000
|
15000
|
|
|
$C$3
|
знач
Х1В
|
0
|
0
|
|
|
$D$3
|
знач
Х2А
|
19350
|
19350
|
|
|
$E$3
|
знач
Х2В
|
0
|
0
|
|
|
$F$3
|
знач
Х3А
|
24961,5
|
24961,5
|
|
|
$G$3
|
знач
Х3В
|
0
|
0
|
|
|
$H$3
|
знач
Х4А
|
32200,335
|
32200,335
|
|
|
$I$3
|
знач
Х4В
|
0
|
0
|
|
Ограничения
|
|
|
|
|
|
|
Ячейка
|
Имя
|
Значение
|
Формула
|
Статус
|
Разница
|
|
|
$J$6
|
1-й
год лев часть
|
15000
|
$J$6<=$L$6
|
связанное
|
0
|
|
|
$J$7
|
2-й
год лев часть
|
0
|
$J$7<=$L$7
|
связанное
|
0
|
|
|
$J$8
|
3-й
год лев часть
|
0
|
$J$8<=$L$8
|
связанное
|
0
|
|
|
$J$9
|
4-й
год лев часть
|
-1,09139E-11
|
$J$9<=$L$9
|
связанное
|
0
|