ВСЕРОССИЙСКИЙ
ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Аудиторная
работа
по
дисциплине «Эконометрика»
Вариант № 1
Выполнила:
Проверил:
Липецк
2006г.
Вариант 1.
(наблюдения с 5-25)
Имеются данные о
деятельности крупнейших компаний США в 1996 г. (табл. 1).
Таблица 1
|
п/n
|
Чистый доход, млрд. долл. США
|
Оборот капитала, млрд. долл. США
|
Использованный капитал, млрд. долл.
|
Численность служащих, тыс. чел.
|
Рыночная капитализация
компании, млрд. долл. США
|
|
|
Y
|
X1
|
X2
|
X3
|
X4
|
|
1
|
0,9
|
31,3
|
18,9
|
43,0
|
40,9
|
|
2
|
1,7
|
13,4
|
13,7
|
64,7
|
40,5
|
…………………………………………………………………..
|
25
|
0,7
|
15,5
|
5,8
|
80,8
|
27,2
|
Задание
1.Рассчитайте матрицу
парных коэффициентов корреляции; оцените статистическую значимость коэффициентов
корреляции.
2.Рассчитайте параметры
линейного уравнения множественной регрессии с полным перечнем факторов.
3.Оцените статистическую
значимость параметров регрессионной модели с помощью t-критерия; нулевую
гипотезу о значимости уравнения проверьте с помощью F-критерия; оцените качество
уравнения регрессии с помощью
коэффициента детерминации 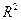 .
.
4.Дайте сравнительную
оценку силы связи факторов с результатом с помощью коэффициентов эластичности,
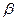 и
и 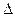 коэффициентов.
коэффициентов.
5.Оцените точность
уравнения через среднюю относительную ошибку аппроксимации.
6.Отберите информативные
факторы в модель по t-критерию
для коэффициентов регрессии. Постройте
модель только с информативными факторами и оцените ее параметры.
7.Рассчитайте прогнозное
значение результата, если прогнозные значения факторов составляют 80% от их
максимальных значений.
8.Рассчитайте ошибки и
доверительный интервал прогноза для уровня значимости 5 или 10% (а = 0,05; а =
0,10).
Выбор признаков для построения модели регрессии:
Предварительно
выполняем корреляционный анализ данных (в Excel в пакете Анализ
данных), для чего:
ü
Введём исходные данные в Excel, располагая их в
смежных диапазонах ячеек (рис.1.1);
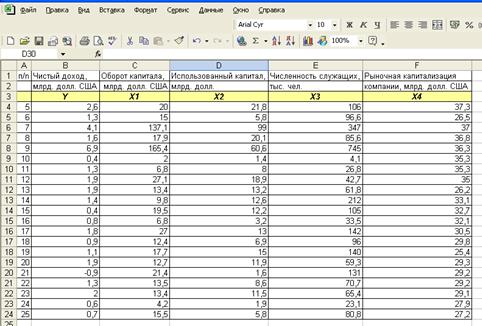
рис.1.1
рис.1.1
ü
Выберем команду Сервис=>Анализ
данных;
ü В диалоговом окне Анализ
данных выберем строку корреляция и подтвердим кнопкой ОК (рис1.2):

рис1.2
ü На табло Корреляция в поле Входной интервал
введём диапазон исходных данных. Если выделяются заголовки, то ставится флажок
в Метке первой строки (рис.1.3):
рис.1.3
Анализ матрицы коэффициентов парной корреляции
(рис.1.4.):
ü зависимая переменная y , т.е. чистый
доход имеет тесную связь с использованным капиталом – x5 (ryx5=0.445), c численностью
служащих – x3 (ryx3=0.786), с оборотом капитала x2 (ryx2=0.861);
рис.1.4
ü факторы x5 и x3 (rx3x5=0,501),
что свидетельствует об отсутствии мультиколлинеарности
(линейная или близкая связь между факторами), поэтому из двух переменных
оставим использованный капитал;
ü первоначально имели n=20, m=4, после
исключения незначимых факторов получили n=20, k=2, т.е. в
модель включается только два фактора;
Выбор вида модели и расчёт ее параметров:
На основе корреляционного
анализа выбираем линейную двухфакторную модель регрессии и для дальнейших
расчётов составляем новую таблицу исходных данных (рис.1.5):
рис.1.5
Оценку параметров модели
выполняем с помощью МНК в матричном виде:
А = (X’X)-1X’Y
В общем виде имеем:
Первоначально транспонируем матрицу X (в Excel=>ТРАНСП),
затем её умножаем на исходную матрицу X (в Excel=>МУМНОЖ)
и вычислим обратную матрицу (в Excel=>МОБР).
После этого обратную матрицу умножим на транспонируемую и на У (в Excel=>МУМНОЖ), (рис.1.6.):
рис.1.6.
Уравнение регрессии зависимости
чистого дохода у от оборота капитала x1 и использованного капитала x2 можно
записать в следующем виде:
у=0,680+0,034x1-0.004x2
Расчётные значения У
определяются путём последовательной подстановки в эту модель значений факторов,
взятых для каждого наблюдения.
Для проведения
регрессионного анализа выполним следующие действия:
ü Выберем команду Сервис=>Анализ
данных;
ü В диалоговом окне Анализ данных выберем
инструмент Регрессия, а затем щёлкнем на кнопку ОК, (рис.1.7):
рис.1.7
ü В диалоговом окне Регрессия в поле Входной
интервал У введём адрес одного диапазона ячеек, который представляет зависимую
переменную. В поле Входной интервал Х введём адреса одного или нескольких
диапазонов, которые содержат значения независимых переменных;
ü Выберем параметры вывода (Новая рабочая книга);
ü В поле Остатки поставим необходимые флажки;
ü ОК (рис.1.8):
рис.1.8
Результат
регрессионного анализа (рис.1.9; рис.1.10):
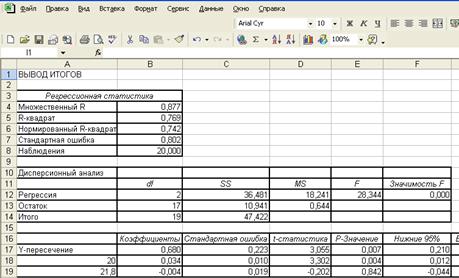
рис.1.9
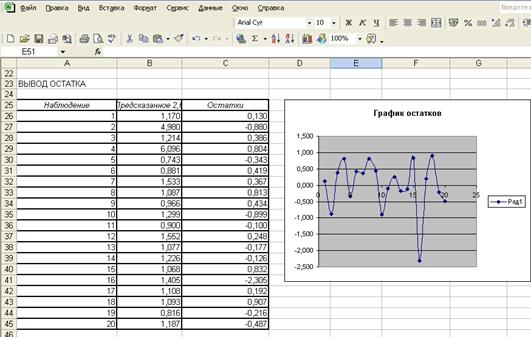
рис.1.10
Оценим
качества всего уравнения регрессии:
Зная
предсказанные по модели значения зависимой переменной У и значения остаточной
компоненты можно рассчитать значения коэффициента детерминации:
Коэффициент R2 показывает долю вариации результативного признака под
воздействием изучаемых факторов, т.е. 76,9 % вариации зависимой переменной
учтено в модели и обусловлено влиянием факторов оборота капитала и фактора
использования капитала.
Коэффициент множественной
корреляции 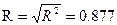 , что означает тесноту связи зависимой переменной У-чистый
доход с факторами оборот капитала и использование капитала на 87,7%.
, что означает тесноту связи зависимой переменной У-чистый
доход с факторами оборот капитала и использование капитала на 87,7%.
Проверка значимости уравнения
регрессии производится по F-критерию Фишера по формуле:
Табличное значение F-критерия
при уровне значимости 0,05 и степенях свободы v1=k=2 b v2=n – k - 1=20-2-1=17 составляет 3,592. Поскольку Fрасч>Fтабл,
то уравнение регрессии адекватно описывает реальный процесс.
Оценка статистической
значимости коэффициентов множественной регрессии оценивается по t-критерию Стьюдента, значения которого вычисляются по
формулам:
taj=aj/Saj, Saj=Se*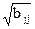 ,
,
где
bjj – диагональный
элемент матрицы (X’X)-1:
Поскольку tрасч>tтабл=3,222 (в Excel=>СТЬЮДРАСПОБР),
то а0,а1 значимы.
Анализ влияния факторов оборота
капитала и использования капитала на независимую переменную У – чистый доход
вычисляется по коэффициенту эластичности и 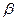 -коэффициентов:
-коэффициентов:
Э1=0,034*27,552/1,619=0,5786
Э2=-0,004*16,810/1,619=0,042
При изменении оборота капитала
чистый доход изменится на 57,86%, а при изменении фактора использование
капитала на 4,2%;
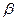 1=0,034*0,010/0,223=0,0015
1=0,034*0,010/0,223=0,0015
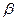 2=-0,004*0,019/0,223=0,003
2=-0,004*0,019/0,223=0,003
Бета-коэффициент показывает,
на какую часть величины СКО меняется среднее значение у с изменением j-ой независимой переменной на одно СКО отклонение при
неизменных остальных независимых переменных. Так, что при увеличении оборота
капитала чистый доход увеличится на 34 тыс.руб., а при увеличении
использованного капитала чистый доход увеличится на 76 тыс.руб.
Случайный
характер остатков проверяется по графику остатков (рис.1.11):
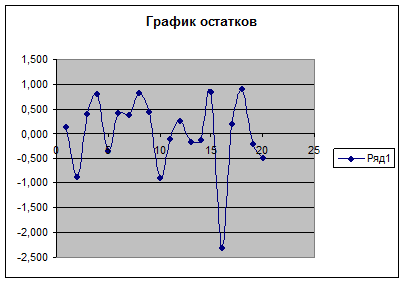
На графике нет направленности в расположении точек Е1,
то Еi - случайные величины, следовательно теоретические
у хорошо аппроксимируют фактические у. таким образом средняя величина остатков
равна 0 и, следовательно, остатки не зависят от значений факторов х, Еотн=1,391%, она меньше 7% - модель имеет
хорошее качество.
Рассчитаем прогнозные значения х1 и х2
при хпрог=хмах*0,8
хпрог1=165,4*0,8=132,32
хпрог2=60,6*0,8=48,48
Рассчитаем точечный и интервальный прогноз:
С помощью Мастера
диаграмм в Excel для фактора оборот капитала и использование капитала подберём
модель тренда (рис.1.11, 1.12):
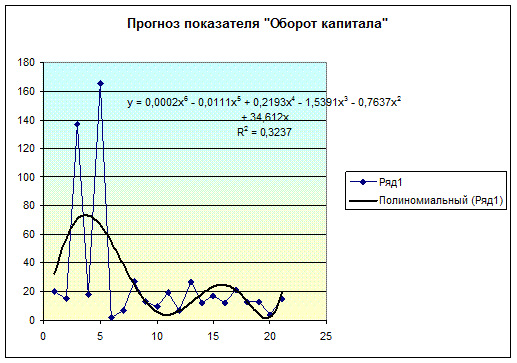
рис.1.11
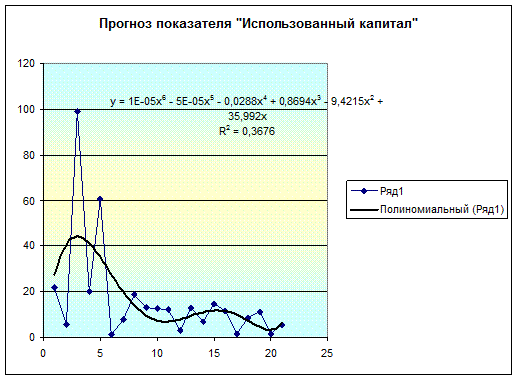
1.12
Для
фактора оборот капитала:
|
Упреждение
|
Прогноз
|
|
1
|
0,056
|
|
2
|
0,037
|
Для
фактора используемый капитал:
|
Упреждение
|
Прогноз
|
|
1
|
0,012
|
|
2
|
0,044
|
Для
получения точечного прогноза по модели у=0,680+0,034х1-0,004х2
необходимо подставить в неё найденные прогнозные значения факторов оборот
капитала и используемый капитал:
Уt21=0.680+0.034*0.056-0.004*0.037=0.6818
Уt22=0.680+0.034*0.012-0.004*0.044=0.6802
Далее рассчитаем
доверительный интервал прогноза: