Содержание
Введение…………………………………………………………
………………..3
1. Теоретическая
часть…………………………………………………………....5
1.1. Классификация и
группировка как метод обработки и анализа
первичной статистической информации…………………………………..5
1.2. Виды группировок. Статистическая
таблица…………………………..…10
2. Расчетная часть………………………………………………………………..13 Задание №1………………………………………………………………….……13
Задание №2………………………………………………………………….…18
Задание №3…………………………………………………………………….24
Задание №4…………………………………………………………………….26
3. Аналитическая часть ………………………………………………………….30
Заключение……………………………………………………………………….36
Список использованной литературы:………………………………………..38
Введение
Роль статистики при переходе к
рыночным отношениям, как известно, возрастает. Статистика выступает не только
как действенный инструмент анализа рыночной экономики, но и как своеобразный
арбитр по оценке условий и результатов ее развития, одновременно являясь мощным
орудием преобразования рыночных социально – экономических отношений, важным
дополнительным фактором оперативного, предприимчивого и эффективного их
совершенствования.
Статистические исследования
предприятий предполагает проведение статистического наблюдения, организацию
сбора статистической информации о предприятиях, ее систематизации и
классификации. Это позволяет с помощью статистических методов получить
обобщающие характеристики и выявить закономерности, существующие в сфере
трудовой деятельности в конкретных условиях места и времени.
Целью данной курсовой работы является анализ деятельности
организаций (предприятий) и использование статистических методов в оценке их
результативности.
В теоретической части курсовой
работы рассмотрены следующие аспекты:
1) Классификация и группировка как метод обработки и анализа
первичной статистической информации.
2) Виды группировок. Статистическая таблица
Расчетная часть курсовой работы
включает решение четырех задач:
1) Работа с таблицей «Статистическая
информация о результатах производственной деятельности
организации»
2) Методами аналитической группировки и корреляционной таблицы,
установить среднесписочную численность работников и выпуск продукции. Измерить
тесноту корреляционной связи.
3) По результатам выполнения задания 1 с вероятностью 0,954
определить:
- ошибку выборки среднего выпуска продукции и границы
- ошибку выборки доли организаций
4) Работа с таблицей «Производство
продукции и среднесписочная численность работников»
Аналитическая часть работы включает в себя
анализ данных, представленных в таблице «Данные
о величине собственного капитала и прибыли Российских предприятий за 2005г»
При работе с табличными данными использовался табличный
процессор Excel пакета Microsoft Office XP.
1.
Теоретическая часть
1.1. Классификация и
группировка как метод обработки и анализа первичной статистической информации
В практической статистике широко применяется метод
классификаций и группировок. Классификация
- это систематическое распределение явлений
и объектов по определенным группам, классам,
разрядам на основании их сходства и различия. Используют классификации:
отраслевую; профессиональную; основных фондов; капитальных вложений;
строительных машин. В статистике внешней торговли используется «Товарная
номенклатура внешнеэкономической деятельности». В условиях возникновения новых
форм хозяйствования начинают использоваться классификаторы форм собственности,
организационно-правовых форм хозяйствующих субъектов.
Для
дальнейшей обработки собранных в ходе статистического наблюдения первичных
данных широко используют и метод группировки.
Группировка
- это распределение множества единиц исследуемой совокупности по группам в
соответствии с существенным для данной группы признаком. Метод группировки
позволяет обеспечивать первичное обобщение данных, представление их в более
упорядоченном виде. Благодаря группировке можно соотнести сводные показатели по
совокупности в целом со сводными показателями по группам. Появляется
возможность сравнивать, анализировать причины различий между группами, изучать
взаимосвязи между признаками.
Группировка позволяет делать вывод о
структуре совокупности и о роли отдельных групп этой совокупности. Именно
группировка формирует основу для последующей сводки и анализа данных.
Признаки, по которым проводится группировка,
называют группировочными
признаками. Группировочный признак иногда называют основанием группировки.
Правильный выбор существенного группировочного признака дает возможность
сделать научно обоснованные выводы по результатам статистического исследования.
Группировочные признаки могут иметь как количественное выражение (объем, доход,
курс валюты, возраст и т.д.), так и качественное
(форма собственности предприятия, пол человека, отраслевая принадлежность,
семейное положение и т.д.).
При
определении числа групп, как правило, учитываются задача исследования, объем
совокупности и виды признаков, которые берутся в качестве основания
группировки. Например, по количественному признаку возраст населения может быть
разбит на самые различные группы. Их число будет зависеть от поставленных
задач. Например, это могут быть группы по возрасту трудоспособного населения;
экономически активного населения и т.д.
Если
берется, предположим, такой качественный признак, как образование, то групп
будет ровно столько, сколько существует ступеней или профилей образования. В
образовании по ступеням групп будет шесть (неполное среднее; среднее; неполное
среднее специальное; специальное среднее; неполное высшее; высшее). По профилю
образования количество групп может совпадать или с числом профессиональных
групп, или с числом сфер образования (гуманитарное; инженерно-техническое;
естественнонаучное).
Если
для построения группировки используется только один признак, то такую
группировку называются простой, если
группировка проводится по нескольким признакам, ее называют сложной. Сложная группировка бывает или
комбинационная, или многомерная.
Комбинационная
группировка выполняется последовательно: группы,
выделенные по одному признаку, затем выделяются в подгруппы по другому
признаку, которые, в свою очередь, могут выделяться по следующему другому
признаку. В этом случае число групп будет равно произведению числа выделенных
групп на число группировочных признаков. Процедура определения оптимального
числа групп основана на применении формулы Стерджесса:
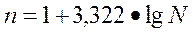
где n - число групп;
N - число единиц
совокупности.
Из
формулы видно, что выбор числа групп зависит от объема совокупности. Если групп
оказывается много, и они включают малое число единиц, то групповые показатели
могут стать ненадежными. Поэтому альтернативой комбинационной группировке
является многомерная
группировка, которая осуществляется по комплексу признаков одновременно.
Ее применение требует использования электронной вычислительной техники. С помощью
специально разработанных электронных программ формируются однородные группы на
основании близости по всему комплексу признаков.
Определение
числа групп тесно связано с понятием величина интервала:
чем больше число групп, тем меньше величина интервала, и наоборот.
Интервал
- разница между максимальным и минимальным значениями признака в каждой группе.
Он определяет количественные границы групп, что для статистической практики
имеет большое значение, особенно когда нужно образовать качественно однородные
группы. Например, исследуется совокупность предприятий по выполнению
коллективных договоров. Здесь нельзя объединять предприятия, которые не
выполнили обязательства, и те, которые их перевыполнили. Показатель здесь -
величина интервала.
Другим
примером является невозможность образовывать группу 95 - 105%, поскольку это
разные части совокупности. Следует образовать две группы: 95 - 100% и 101 -
105%. В этом случае границы, по которым различаются совокупности, абсолютно
соблюдаются.
Каждый
интервал имеет нижнюю
(наименьшее значение признака) и верхнюю (наибольшее значение признака) границы или
одну из них. Поэтому величина интервала есть разность между верхней и нижней
границами интервала. Если у интервала указана лишь одна граница (у первого -
верхняя, у последнего - нижняя), то речь идет об открытых интервалах. Если у интервала имеются и нижняя, и
верхняя границы, то речь идет о закрытых интервалах.
Закрытые интервалы подразделяются на равные и неравные (прогрессивно
возрастающие, прогрессивно убывающие), а также специализированные и
произвольные.
Группировку
с равными интервалами
строят тогда, когда исследуются количественные различия в величине признака
внутри групп одинакового качества, а также если распределение носит более или
менее равномерный характер. Если можно заранее установить определенное
количество групп, то величину равного интервала можно вычислить по формуле:
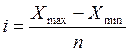
где i - величина равного интервала;
xmax , xmin
- наибольшее и наименьшее значения признака;
n - число групп.
Если
не требуется предварительного установления числа групп, то используется другой
способ определения величины равного интервала - по формуле Стерджесса:
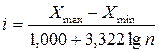
где
n - число наблюдений.
Если
величина равного интервала рассчитывается по данной формуле, то следует
знаменатель предварительно округлить до целого числа (как правило, всегда
большего), так как количество групп не может быть дробным числом.
В
статистической практике чаще применяются
неравные интервалы (постепенно возрастающие или
постепенно убывающие). При этом исследуемая совокупность делится на группы
примерно равного заполнения с большим числом единиц. Неравные интервалы могут
использоваться, например, в таких случаях:
а)
при исследовании группировки с применением нескольких признаков, дающих
возможность составить несколько подгрупп, где требуются уже и более длинные и
более короткие интервалы;
б)
при образовании крупных групп с новым качеством на базе мелких групп при
условии сохранения их однородности, что приводит к увеличению интервалов.
В
статистической практике используются также специализированные
интервалы. Интервалы называют специализированными, если речь идет об
установлении границ интервала в группах, схожих по типу и по признаку, но
имеющих отношение, скажем, к разным отраслям производства.
1.2. Виды группировок. Статистическая таблица
Виды
группировок зависят от целей и задач, которые они выполняют. С помощью метода
статистических группировок выделяют качественно однородные совокупности,
изучают структуры совокупности и изменения, происходящие в них, а также решают
задачи по исследованию существующих связей и зависимостей.
С
известной мерой условности для выполнения этих задач группировки соответственно
делят на типологические, структурные и аналитические.
Метод
типологической группировки
заключается в выявлении в качественно разнородной совокупности однородных
групп. При этом очень важно правильно отобрать группировочный признак, который
поможет идентифицировать выбранный тип. Типологические группировки широко
применяются в исследовании социально-экономических явлений. Примерами такого
вида группировок могут быть объемы производства продукции по федеральным
округам, по формам хозяйствования, социальные группы населения и т.д. В типологических
группировках часто используются специализированные интервалы.
Метод
структурной группировки есть разделение однородной совокупности на группы по
тому или иному варьирующему группировочному признаку. Примерами такого вида
группировок могут быть группы населения по полу, возрасту, месту проживания,
доходу и т.д., то есть может решаться задача по изучению структурного состава
той или иной однородной совокупности, структурных изменений по тому или иному
группировочному признаку. На основе структурных изменений изучаются
закономерности общественных явлений.
Метод аналитической группировки заключается в
исследовании взаимосвязей между факторными признаками в качественно однородной
совокупности. С помощью аналитических группировок удается выявлять признаки,
которые могут выступать или причиной, или следствием того или иного явления. В
аналитических группировках чаще всего используются неравные интервалы.
Результаты
группировочного материала оформляются в виде таблиц, где он излагается в
наглядно-рациональной форме. Не всякая таблица может быть статистической.
Табличные формы календарей, тестовых и опросных листов, таблица умножения не
являются статистическими.
Статистическая таблица
- это цифровое выражение итоговой характеристики всей наблюдаемой совокупности
или ее составных частей по одному или нескольким существенным признакам.
Статистическая таблица содержит два элемента: подлежащее и сказуемое.
Подлежащее
статистической таблицы есть перечень групп или единиц,
составляющих исследуемую совокупность единиц наблюдения.
Сказуемое статистической
таблицы - это цифровые показатели, с помощью которых дается
характеристика выделенных в подлежащем групп и единиц.
Различают
простые, групповые и комбинационные таблицы.
В простых таблицах, как правило, содержится справочный
материал, где дается перечень групп или единиц, составляющих объект изучения.
При этом части подлежащего не являются группами одинакового качества,
отсутствует систематизация изучаемых единиц. Сказуемое этих таблиц содержит
абсолютные величины, отражающие объемы изучаемых процессов.
Групповые
и комбинационные таблицы предназначены для научных целей, где, в отличие от
простых таблиц, в сказуемом - средние и относительные величины на основе
абсолютных величин.
Групповая таблица
- это таблица, где статистическая совокупность разбивается на отдельные группы
по какому-либо одному существенному признаку, при этом каждая группа
характеризуется рядом показателей. Примером такой группировки может быть
разделение российских семей на группы по месту проживания (сельское и
городское), где образуются подгруппы семей по количеству детей. Анализ этих
группировок по материалам переписи 1989 года позволил сделать вывод, что
большинство семей, независимо от принадлежности к городскому или сельскому
населению, имеют только по одному ребенку.
Комбинационная таблица
- это таблица, где подлежащее представляет собой группировку единиц
совокупности по двум и более признакам, которые распределяются на группы
сначала по одному признаку, а затем на подгруппы по другому признаку внутри
каждой из уже выделенных групп. Комбинационная таблица устанавливает
существенную связь между факторами группировки. Примером комбинационной
группировки может быть распределение полиграфических предприятий по трем
существенным признакам: степени оснащенности современным полиграфическим
оборудованием, степени применения современных технологий и уровню
производительности труда. Такого рода статистические таблицы позволяют
осуществить всесторонний анализ, но они менее наглядны.
При
составлении таблиц необходимо соблюдать общие правила:
-
таблица должна быть легко обозримой;
-
общий заголовок должен кратко выражать
основное содержание;
-
наличие строк «общих итогов»;
-
наличие нумерации строк, которые
заполняются данными;
-
соблюдение правила округления чисел.
2.Расчетная
часть
Задание №1
Имеются следующие выборочные
данные о деятельности организаций за год.
Таблица 1.1
Статистическая информация о результатах
производственной деятельности организации
|
№
организации
|
Среднесписочная численность работников, чел.
|
Выпуск продукции, млн руб.
|
Фонд заработной платы, млн руб.
|
Затраты на производство продукции, млн руб.
|
|
1
|
162
|
36,45
|
11,340
|
30,255
|
|
2
|
156
|
23,4
|
8,112
|
20,124
|
|
3
|
179
|
46,540
|
15,036
|
38,163
|
|
4
|
194
|
59,752
|
19,012
|
47,204
|
|
5
|
165
|
41,415
|
13,035
|
33,546
|
|
6
|
158
|
26,86
|
8,532
|
22,831
|
|
7
|
220
|
79,2
|
26,400
|
60,984
|
|
8
|
190
|
54,720
|
7.100
|
43,776
|
|
9
|
163
|
40,424
|
12,062
|
33,148
|
|
10
|
159
|
30,21
|
9,540
|
25,376
|
|
11
|
167
|
42,418
|
13,694
|
34,359
|
|
12
|
205
|
64,575
|
21,320
|
51,014
|
|
13
|
187
|
51,612
|
16,082
|
41,806
|
|
14
|
161
|
35,42
|
10,465
|
29,753
|
|
15
|
120
|
14,4
|
4,32
|
12,528
|
|
16
|
162
|
36,936
|
11,502
|
31,026
|
|
17
|
188
|
53,392
|
16,356
|
42,714
|
|
18
|
164
|
41,0
|
12,792
|
33,62
|
|
19
|
192
|
55,680
|
17,472
|
43,987
|
|
20
|
130
|
18,2
|
5,85
|
15,652
|
|
21
|
159
|
31,8
|
9,858
|
26,394
|
|
22
|
162
|
.39,204
|
11,826
|
32,539
|
|
23
|
193
|
57,128
|
18,142
|
45,702
|
|
24
|
158
|
28,44
|
8,848
|
23,89
|
|
25
|
168
|
43,344
|
13,944
|
35,542
|
|
26
|
208
|
70,720
|
23,920
|
54,454
|
|
27
|
166
|
41,832
|
13,280
|
34,302
|
|
28
|
207
|
69,345
|
22,356
|
54,089
|
|
29
|
161
|
35,903
|
10,948
|
30,159
|
|
30
|
186
|
50,220
|
15,810
|
40,678
|
а)
построить статистический ряд распределения предприятий по признаку выпуск
продукции, образовав пять групп с равными интервалами;
б) построить графики полученного ряда распределения. Графически
определить значения моды и медианы;
в) рассчитать характеристики ряда
распределения: среднюю арифметическую, среднее квадратическое отклонение,
коэффициент вариации;
г) вычислить среднюю арифметическую по
исходным данным, сравнить её с аналогичным показателем, рассчитанным в пункте
в) настоящего задания. Объяснить причину их расхождения.
Сделать выводы по результатам выполнения задания
Решение:
Для того чтобы разбить данные организации на
пять групп с равными интервалами по размерам выпуска продукции, необходимо
рассчитать величину шага разбиения по формуле:
i = (Xmax - Xmin) / n, где n – число образуемых групп.
i = (79,2
– 14,4) / 5 = 12,96 (млн. руб.)
Распределение организаций по группам по выпуску
продукции представлено в таблице 1.2:
Таблица
1.2
|
№ группы
|
Группы организаций по
выпуску продукции, млн. руб.
|
Кол-во организаций
|
Кумулятивная частота
|
|
1
|
14.4-27,36
|
4
|
4
|
|
2
|
27,36-40,32
|
8
|
12
|
|
3
|
40,32-53,28
|
9
|
21
|
|
4
|
53,28-66,24
|
6
|
27
|
|
5
|
66,24-79,2
|
3
|
30
|
|
Итого:
|
30
|
-
|
Согласно данным таблицы 1.2 построим графики полученного ряда
распределения.
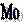


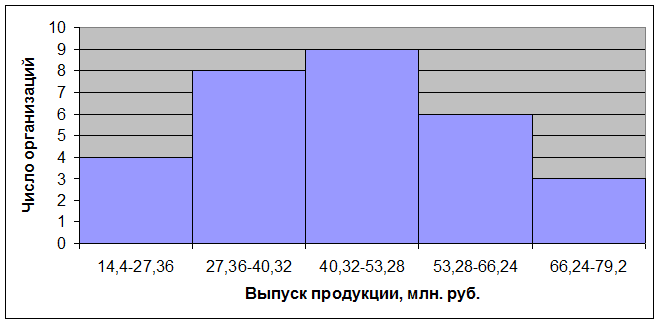
 Рис.
1: Гистограмма распределения организаций по выпуску продукции
Рис.
1: Гистограмма распределения организаций по выпуску продукции
Мода размера выпуска
продукции:
f2 – f1 9–
8
Mо = x0 + d ——————— = 40,32 + 12,96 ————— = 43.56 (млн. руб.)
( f2 – f1 ) + (f2 - f3 ) (9 – 8) + (9 - 6)


 значит, наиболее распространенный
размер выпуска продукции среди организаций составляет 43.56 млн. руб.
значит, наиболее распространенный
размер выпуска продукции среди организаций составляет 43.56 млн. руб.
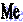 Рис.
2: Кумулята распределения организаций по
выпуску продукции.
Рис.
2: Кумулята распределения организаций по
выпуску продукции.
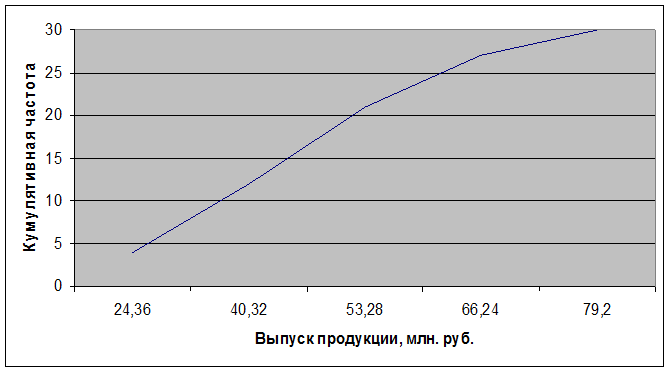
Медиана
размера выпуска продукции:
(∑f) : 2 - SMe-1 30 : 2 -12
Me
= x0 + d —————— = 40,32 +
12,96 ————— = 44,64 (млн. руб.)
fMe
9
значит, 50%
организаций имеют размер выпуска продукции менее 44,64 млн. руб., а 50% - более
44,64 млн. руб.
Для расчёта средней арифметической, среднего
квадратического отклонения, коэффициента вариации применяем формулы во
взвешенной форме, так как данные сгруппированы и представлены в виде
интервального ряда.
Для расчета указанных величин нам понадобятся некоторые
промежуточные данные, представленные в таблице 1.3:
Таблица 1.3
|
№ группы
|
Группы предприятий по выпуску продукции, млн. руб.
|
Число предприятий
(fi)
|
Середина интервала (хi)
|
хi* fi
|
хi-ха
|
(хi-ха)2* fi
|
|
1
|
14,4-27,36
|
4
|
20,88
|
83,52
|
-24,192
|
2341
|
|
2
|
27,36-40,32
|
8
|
33,84
|
270,72
|
-11,232
|
1009
|
|
3
|
40,32-53,28
|
9
|
46,8
|
421,2
|
1,728
|
27
|
|
4
|
53,28-66,24
|
6
|
59,76
|
358,56
|
14,688
|
1294
|
|
5
|
66,24-79,2
|
3
|
72,72
|
218,16
|
27,648
|
2293
|
|
Итого:
|
-
|
30
|
-
|
1352,16
|
-
|
6964
|
Данные для расчёта средней арифметической, среднего квадратического
отклонения, коэффициента вариации
1) Для расчёта средней арифметической используется
следующая формула:
ха = ∑ хifi / ∑ fi = 1352,16/30 = 45,072 (млн. руб.)
2) Дисперсия:
Dх = ∑(хi-ха)2
fi / ∑ fi = 6964 / 30 = 232,13 (млн. руб.)
3) Среднее квадратическое отклонение
вычисляется по формуле:
σ = ∑(хi-ха)2
fi / ∑ fi = 232,13 = 15,2 (млн. руб.)
4) Тогда коэффициент
вариации будет равен:
Vδ = σ /ха = (15,2 /
45,072)100 = 33,7 %
Таблица 1.4.
Результаты
расчёта средней арифметической, среднего
квадратического отклонения, коэффициента вариации
|
№ п/п
|
Показатель
|
Значение
|
|
1
|
Средняя арифметическая, (ха),
млн. руб.
|
45,072
|
|
2
|
Дисперсия
|
232,13
|
|
3
|
Среднее квадратическое
отклонение, млн. руб.
|
15,2
|
|
4
|
Коэффициент вариации,%
|
33,7
|
Теперь
вычислим среднюю арифметическую по данным таблицы 1.2, расчёт будем производить
по формуле:
ха = ∑ хi / n = 1320,54 / 30 = 44,018 (млн. руб.)
Полученный результат
отличен от приведённого выше, так как в данном случае расчет проводился для не сгруппированных
данных, представленных в виде дискретного ряда. Следовательно, расчёт
проводился по формуле средней арифметической простой.
Вывод.
Таким образом, по результатам
задания №1 можно сделать такой вывод: размер выпуска продукции организаций отличается
от среднего размера выпуска продукции в среднем на 15,2 млн. руб., что
составляет 33,7%. Это значение Vδ превышает 33%, что говорит о неоднородности
совокупности предприятий по выпуску продукции.
Задание №2
По исходным данным таблицы 1.1:
а) установить наличие и характер связи между признаками выпуск
продукции и среднесписочная численность работников, образовав пять групп с
равными интервалами по обоим признакам, методами:
-
аналитической группировки;
-
корреляционной таблицы;
б) измерить тесноту корреляционной связи между названными
признаками с использованием коэффициента детерминации и эмпирического
корреляционного отношения.
Сделать выводы.
Решение:
Сначала установим связь между указанными признаками методом
аналитической группировки. В качестве факторного признака будет выступать
среднесписочная численность работников, а в качестве результативного – выпуск
продукции. Сначала необходимо рассчитать величину интервала: i = (220 – 120) / 5 = 20
(млн. руб.)
Результаты группировки отражены в таблице 2.1.
Таблица
2.1.
Зависимость
выпуска продукции от среднесписочной численности работников.
|
№ группы
|
Группировка предприятий по
среднесписочной численности работников., чел.
|
№ предприятия
|
Выпуск продукции
млн.руб
У
|
Среднесписочная численность
работников.
Х
|
У2
|
|
I
|
120-140
|
15
|
14,4
|
120
|
207,36
|
|
20
|
18,2
|
130
|
331,24
|
|
S
|
|
2
|
36,2
|
250
|
538,6
|
|
В среднем на 1 предприятие
|
18,1
|
125
|
|
|
II
|
140-160
|
2
|
23,4
|
156
|
547,56
|
|
6
|
26,86
|
158
|
721,46
|
|
10
|
30,21
|
159
|
912,64
|
|
21
|
31,8
|
159
|
1011,24
|
|
24
|
28,44
|
158
|
808,83
|
|
S
|
|
5
|
140,71
|
790
|
4001,73
|
|
В среднем на 1 предприятие
|
28,14
|
158
|
|
|
III
|
160-180
|
1
|
36,45
|
162
|
1328,6
|
|
3
|
46,540
|
179
|
2165,97
|
|
5
|
41,415
|
165
|
1715,2
|
|
9
|
40,424
|
163
|
1634,09
|
|
11
|
42,418
|
167
|
1799,28
|
|
14
|
35,42
|
161
|
1254,57
|
|
16
|
36,936
|
162
|
1364,26
|
|
18
|
41,0
|
164
|
1681
|
|
22
|
39,204
|
162
|
1536,95
|
|
25
|
43,344
|
168
|
1878,7
|
|
27
|
41,832
|
166
|
1749,91
|
|
29
|
35,903
|
161
|
1289,02
|
|
S
|
|
12
|
480,886
|
1980
|
19397,55
|
|
В среднем на 1 предприятие
|
40,07
|
165
|
|
|
IV
|
180-200
|
4
|
59,752
|
194
|
3570,3
|
|
8
|
54,720
|
190
|
2994,27
|
|
13
|
51,612
|
187
|
2663,79
|
|
17
|
53,392
|
188
|
2850,7
|
|
19
|
55,680
|
192
|
3100,26
|
|
23
|
57,128
|
193
|
3263,6
|
|
30
|
50,220
|
186
|
2522,04
|
|
S
|
|
7
|
382,504
|
1330
|
20964,96
|
|
В среднем на 1 предприятие
|
54,6
|
190
|
|
|
V
|
200-220
|
7
|
79,2
|
220
|
6272,64
|
|
12
|
64,575
|
205
|
4169,93
|
|
26
|
70,720
|
208
|
5001,31
|
|
28
|
69,345
|
207
|
4808,73
|
|
S
|
|
4
|
283,84
|
840
|
20252,61
|
|
В среднем на 1 предприятие
|
70,96
|
210
|
|
|
S
|
ИТОГО
|
1324,14
|
5190
|
|
|
|
В среднем
|
264,828
|
1038
|
Теперь по
данным рабочей таблицы строим итоговую аналитическую таблицу:
Таблица
2.2
|
Группировка предприятий по
среднесписочной численности работников., чел.
|
Число пр-тий
|
Выпуск продукции, млн. руб.
|
Среднесписочная численность
работников, чел.
|
|
Всего
|
В среднем на одно пр-тие
|
Всего
|
В среднем на одно пр-тие
|
|
120-140
|
2
|
36,2
|
18,1
|
250
|
125
|
|
140-160
|
5
|
140,71
|
28,14
|
790
|
158
|
|
160-180
|
12
|
480,886
|
40,07
|
1980
|
165
|
|
180-200
|
7
|
382,504
|
54,6
|
1330
|
190
|
|
200-220
|
4
|
283,84
|
70,96
|
840
|
210
|
|
S
|
30
|
1324,14
|
211,87
|
5190
|
848
|
По данным аналитической таблицы мы видим, что с приростом численности
работников, средний выпуск на одно предприятие возрастает. Значит, между
исследуемыми признаками существует прямая корреляционная зависимость.
Для того чтобы определить тесноту взаимосвязи между
факторным и результативным признаком необходимо вычислить эмпирическое
корреляционное отношение - 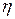 . Корреляционное отношение вычисляется как корень квадратный
из отношения межгрупповой дисперсии к общей дисперсии. Общая дисперсия равна
сумме средней из групповых дисперсий и межгрупповой дисперсии.
. Корреляционное отношение вычисляется как корень квадратный
из отношения межгрупповой дисперсии к общей дисперсии. Общая дисперсия равна
сумме средней из групповых дисперсий и межгрупповой дисперсии.
Вычислим групповые, межгрупповую, среднюю из
групповых и общую дисперсии.
Групповая дисперсия: 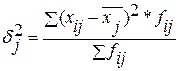 , где :
, где :
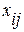 - i-тая варианта результативного признака внутри j-той группы (из таблицы 2.1),
- i-тая варианта результативного признака внутри j-той группы (из таблицы 2.1),
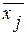 - среднее значение
результативного признака внутри j-той группы (из
таблицы 2.2),
- среднее значение
результативного признака внутри j-той группы (из
таблицы 2.2),
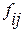 - количество предприятий
внутри группы (из таблицы2.2).
- количество предприятий
внутри группы (из таблицы2.2).
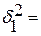 6,8;
6,8; 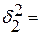 8,6;
8,6; 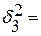 10,4;
10,4; 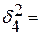 9,07;
9,07; 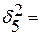 27,8
27,8
Средняя из групповых
дисперсий: 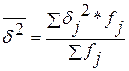
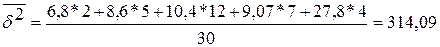 (млн. руб.)
(млн. руб.)
Межгрупповая дисперсия: 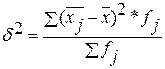 , где:
, где:
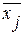 - среднее значение результативного признака внутри j-той группы,
- среднее значение результативного признака внутри j-той группы,
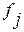 - количество предприятий в j-той
группе,
- количество предприятий в j-той
группе,
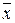 - среднее значение
признака среди исследуемой совокупности.
- среднее значение
признака среди исследуемой совокупности.
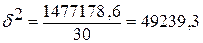
Корреляционное отношение: 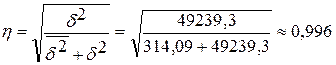
Так как корреляционное отношение 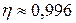 , то можно утверждать о тесной связи между среднесписочной
численностью работников и выпуском продукции.
, то можно утверждать о тесной связи между среднесписочной
численностью работников и выпуском продукции.
Образовав 5 групп с
равными интервалами по обоим признакам, получились данные, представленные в
таблице 2.3:
Таблица 2.3.
Корреляционная
таблица
|
Группы среднесписочной
численности работников
|
120 -
|
140
|
160 -
|
180-
|
200-
|
Часто-та
|
|
Группы предприятий по выпуску продукции
|
140
|
160
|
180
|
200
|
220
|
|
14,4-27,36
|
2
|
2
|
-
|
-
|
-
|
4
|
|
27,36-40,32
|
-
|
3
|
5
|
-
|
-
|
8
|
|
40,32-53,28
|
-
|
-
|
7
|
2
|
-
|
9
|
|
53,28-66,24
|
-
|
-
|
-
|
5
|
1
|
6
|
|
66,24-79,2
|
-
|
-
|
-
|
-
|
3
|
3
|
|
Частота
|
2
|
5
|
12
|
7
|
4
|
30
|
Выводы.
Таким образом, по результатам выполнения задачи №2 можно сделать
следующие выводы:
1) из
таблицы 2.1. видно, что с ростом величины среднесписочной численности
работников от группы к группе, увеличивается и величина выпуска продукции.
Следовательно, связь между рассматриваемыми признаками прямая корреляционная;
2) выводы,
сделанные в п.1) подтверждаются и корреляционной таблицей, где присутствует
ярко выраженное распределение предприятий
вдоль диагонали (таблица 2.3);
3) корреляционное
отношение (0,996, т.е. близко к единице) свидетельствует, что на величину
выпуска продукции существенно влияет величина среднесписочной численности
работников.
Задание №3
По результатам выполнения задания 1 с
вероятностью 0,954 определить:
1. ошибку выборки средней величины продукции
и границы, в которых будет находиться средний выпуск продукции в генеральной
совокупности;
2. ошибку выборки доли организаций с
выпуском продукции 53,28 млн. руб. и более и границы, в которых будет
находиться генеральная доля.
Решение:
1. Ошибка
выборки средней величины продукции и границы 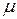 вычисляется как:
вычисляется как: 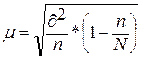 , где:
, где:
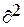 - дисперсия по
признаку среднесписочная численность работников,
- дисперсия по
признаку среднесписочная численность работников,
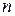 - объем выборочной
совокупности,
- объем выборочной
совокупности,
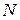 - объем генеральной совокупности.
- объем генеральной совокупности.
Так как по условиям выборка 20%-ная, то 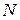 =
=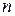 /20*100=30/20*100
/20*100=30/20*100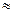 150.
150.
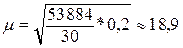 (млн. руб.)
(млн. руб.)
Это означает, что при выборке возможна ошибка18,9 млн.
руб.
Границы, в которых будет находиться средняя величина выпуска
продукции в генеральной совокупности, определяется как 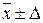 .
.
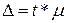 , где t
–
нормированное отклонение и при вероятности 0,954, t=2.
, где t
–
нормированное отклонение и при вероятности 0,954, t=2.
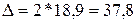 млн. руб.
млн. руб.
Границы, в которых будет находиться средняя величина выпуска
продукции в генеральной совокупности 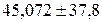 млн. руб., то есть
средняя величина выпуска продукции в генеральной совокупности будет находиться
в промежутке от 7,272 до 82,872 млн. руб.
млн. руб., то есть
средняя величина выпуска продукции в генеральной совокупности будет находиться
в промежутке от 7,272 до 82,872 млн. руб.
2. Ошибка выборки доли организаций с выпуском
продукции 53.28 млн. руб. и более:
Количество предприятий с выпуском продукции 53,28 млн. руб. и более равно
9.
Доля 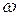 определяется как:
определяется как: 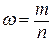 , где:
, где:
m – количество единиц, обладающих признаком,
n – объем совокупности.
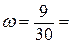 0,3
0,3
Дисперсия доли 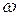 определяется как:
определяется как: 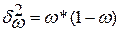 .
.
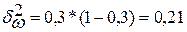
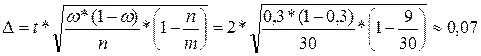
Генеральная доля будет находиться в пределах от 0,23
до 0,37, то есть от 23% до 37% от генеральной совокупности.
Задание № 4
Имеются следующие данные по двум
предприятиям отрасли :
Таблица
3.1
Производство продукции и
среднесписочная численность работников.
|
Филиалы
организаций
|
Базисный
период
|
Отчетный
период
|
|
Выпуск
продукции, млн. руб.
|
Среднесписочная
численность работников, чел.
|
Выпуск
продукции, млн. руб.
|
Среднесписочная
численность работников, чел.
|
|
№
1
|
50
|
180
|
80
|
200
|
|
№
2
|
70
|
200
|
90
|
200
|
Определите
:
1.
Уровни и динамику производительности труда по
каждому филиалу.
2.
По организации в целом:
а) индекс производительности
труда переменного состава; постоянного состава; структурных сдвигов;
б) абсолютное изменение
производительности труда в целом и за счет отдельных факторов
в) абсолютное изменение
выпуска продукции вследствие изменения среднесписочной численности работников,
производительности труда и двух факторов вместе.
Сделайте выводы.
Решение :
1. Построим
расчетную таблицу, где выпуск продукции в базисном периоде обозначим V0, а среднесписочную численность
как V1 и отчетный период как S0 и S1.
Таблица
3.2
|
Филиалы
|
V0=W0*S0
Тыс. руб.
|
V1=W1*S1
Тыс. руб.
|
S0
Чел.
|
S1
Чел.
|
W0=V0:S0
Руб.
|
W1=V1:S1
Руб.
|
Iw=W1:Wo
Руб.
|
W0S1
|
D0=S0:
åT0
Чел
|
D1=S1:
åT1
Чел
|
W0D0
|
W1D1
|
W0D1
|
|
№1
|
50
|
180
|
80
|
200
|
0,625
|
0,9
|
1,44
|
125
|
0,5
|
0,5
|
0,3
|
0,45
|
0,3
|
|
№2
|
70
|
200
|
90
|
200
|
0,7
|
1
|
1,42
|
140
|
0,5
|
0,5
|
0,35
|
0,5
|
0,35
|
|
å
|
120
|
380
|
170
|
400
|
|
|
|
265
|
1
|
1
|
0,65
|
0,95
|
0,65
|
2. а) Для расчета индекса
производительности труда переменного состава
используем следующую формулу :
получаем : Jw=0,95 : 0,7=1,35
Индекс показывает изменение среднего уровня производительности труда в
однородной совокупности под влиянием двух факторов :
1)
изменение качественного показателя W (производительности труда) у
отдельных предприятий;
2)
изменение доли, с которой каждое значение W входит в общий объем совокупности.
Для расчета индекса производительности труда
постоянного состава
используем следующую формулу :
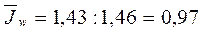 получаем :
получаем :
Индекс показывает изменение среднего уровня только под влиянием изменения
индивидуальных значений качественного показателя в постоянной структуре.
Для расчета индекса влияния
структурных сдвигов в отчетном периоде на динамику средней производительности
труда используем следующую формулу :
получаем : Jw(d)=0,66 : 0,7= 0,94
Рассчитанные выше показатели
взаимосвязаны между собой количественно, это определяется формулой :
получаем :
б) абсолютное
изменение производительности труда в целом и за счет отдельных факторов
J(o) - J(б) = 0,085
в) абсолютное изменение выпуска
продукции вследствие изменения среднесписочной численности работников,
производительности труда и двух факторов вместе.
численность рабочих :
Dq(S) = (S1-S0)W0
получаем : Dq(S) = (200 – 80) * 0,625 = 75
уровень производительности труда
:
Dq(W) = (W1-W0)S1
получаем : Dq(W) = (0,9 – 0,625) * 200 = 55
обоих факторов вместе :
Dq = Dq(S) +Dq(W)
получаем : Dq = 75 + 55 =130
Вывод:
Поскольку индекс производительности труда
переменного состава равен 1,35 или 135%, значит, средняя производительность
труда по двум предприятиям возросла на 35%. Индекс производительности труда
фиксированного состава равен 0,97 или 97%, значит, средняя производительность
труда по двум предприятиям снизилась на 3%. Индекс структурных сдвигов равен
0,94 или 94%, значит, средняя производительность труда по двум предприятиям
снизилась на 6% за счет изменения структуры.
Изменение численности рабочих
привело к снижению производительности труда на 6%. Одновременное воздействие
двух факторов уменьшило среднюю производительность труда по двум предприятиям
на 9%.
2.
Аналитическая
часть
Задачи
статистики состоят в выявлении связи, определении ее направления и ее
измерении. Наиболее же общая задача – это прогнозирование и регулирование
социально-экономических явлений на основе полученных представлений о связях
между явлениями.
Статистика
рассматривает экономический закон как существенную и устойчивую связь между определенными
явлениями и процессами. Познавая связи, статистика познает законы. А их знание
позволяет управлять общественным развитием. Основой изучения связей является
качественный анализ.
Различают два вида признаков:
1)
факторные – те, которые влияют на изменение других
процессов;
2)
результативные – те, которые изменяются под
воздействием других признаков.
В статистике связи классифицируются
по степени их тесноты. Исходя из этого различают функциональную (полную) и
статистическую (неполную, корреляционную) связь.
Функциональная связь – такая
связь, при которой значение результативного признака целиком определяется
значением факторного (например, площадь круга). Она полностью сохраняет свою силу и проявляется во всех случаях
наблюдения и для всех единиц наблюдения. Каждому значению факторного признака
соответствует одно или несколько определенных значений результативного
признака.
Для корреляционной связи характерно то, что одному и тому же значению
факторного признака может соответствовать сколько угодно различных значений
результативного признака. Здесь связь проявляется лишь при достаточно большом
количестве наблюдений и лишь в форме средней величины.
По направлению изменений факторного
и результативного признака различают связь прямую и обратную.
Прямая связь – такая связь, при которой с изменением значений факторного
признака в одну сторону, в ту же сторону меняется и результативный признак.
Обратная связь – такая связь, при которой с увеличением
(уменьшением) факторного признака происходит уменьшение (увеличение)
результативного признака.
По аналитическому выражению
выделяются две основные формы связи:
– прямолинейная
(выражается уравнением прямой);
– криволинейная
(описывается уравнениями кривых линий – гипербол, парабол, степенных функций).
Постановка
задачи
По имеющейся информации о
результатах деятельности 19 Российских
предприятий, стоящих по рейтингу на первых позициях, построим уравнение линейной зависимости
прибыли предприятий от размера собственного капитала.
Таблица 4.1.
Данные о величине собственного капитала и прибыли Российских предприятий
за 2005г.
|
Рейтинг
|
Название предприятия
|
Собственный капитал, млн. руб.
|
прибыль, млн. руб.
|
|
1
|
2
|
3
|
4
|
|
1
|
"Газпром"
|
2780001
|
203448
|
|
2
|
РЖД
|
1826037
|
9751
|
|
3
|
ОАО "Сургутнефтегаз"
|
707913
|
114479
|
|
4
|
РАО "ЕЭС России"
|
386200
|
348400
|
|
5
|
Нефтяная компания
"ЛУКойл"
|
222156
|
66326
|
|
6
|
ГМК "Норильский никель"
|
208143
|
58159
|
|
7
|
ТНК-ВР
|
165000
|
140400
|
|
8
|
"Связьинвест"
|
167572
|
45700
|
|
9
|
Нефтяная компания
"Сибнефть"
|
153000
|
84800
|
|
1
|
2
|
3
|
4
|
|
10
|
АФК "Система"
|
182844
|
16503
|
|
11
|
Сбербанк России
|
148000
|
62929
|
|
12
|
“Татнефть”
|
103653
|
36876
|
|
13
|
"Северсталь"
|
103275
|
34312
|
|
14
|
Нефтегазовая компания
"Славнефть"
|
101270
|
9923
|
|
15
|
Евраз Груп
|
77558
|
29517
|
|
16
|
"Русал"
|
75600
|
28512
|
|
17
|
АК "Транснефть"
|
46629
|
4608
|
|
18
|
АвтоВАЗ
|
43308
|
1400
|
|
19
|
Магнитогорский металлургический
комбинат
|
28500
|
1345
|
Источник: http://www.barrel.ru/
Методика решения задачи
На основании имеющихся данных найдем
уравнение прямой регрессии У на Х, где У – прибыль предприятий (результативный
признак), Х – размер собственного капитала (факторный признак).
Уравнение регрессии имеет вид: У = а + bХ.
Тесноту связи между прибылью
предприятий с помощью линейного коэффициента корреляции rху.
Методика
выполнения расчетов
Статистический анализ выполним с
применением пакета прикладных программ MS Excel в среде Windows.
На рисунке
1 изображено расположение на рабочем листе MS Excel таблицы с исходными данными. 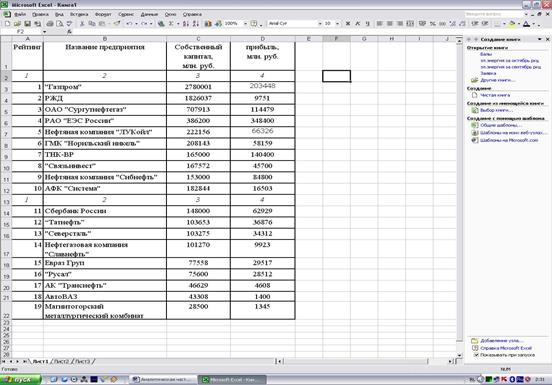
Рис. 3. Исходные данные о результатах деятельности Российских предприятий
В ячейки F3 и G3 введем
формулу для расчета коэффициентов регрессии а и b (Рис. 2):
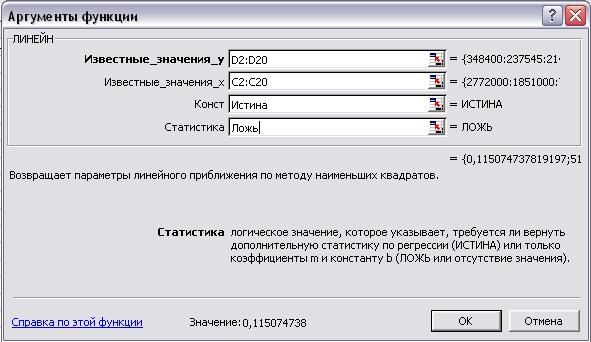
Рис. 4. Расчет коэффициентов регрессии
В ячейку F4 введем формулу для расчета линейного коэффициента
корреляции (Рис.3):
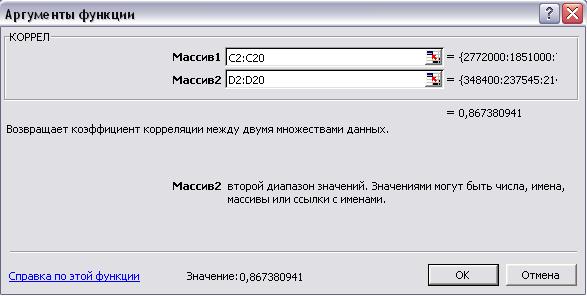
Рис. 5. Расчет коэффициента корреляции
Получили, что коэффициенты
регрессии а = 51,16 и b = 0,042,
таким образом, уравнение зависимости прибыли предприятий (У) от величины
собственного капитала (Х) имеет вид: У = 51,16 + 0,042Х, т.е. при увеличении
размера собственного капитала на 1 млн. руб. прибыль предприятий в среднем
увеличивается на 42 тыс. руб.
Коэффициент корреляции rху = 0,867 свидетельствует о сильной и прямой связи
между размером собственного капитала и прибылью организации.
Изобразим графически исходные
данные о прибыли и размере собственного капитала и полученную прямую зависимости
данных признаков (Рис. 6).
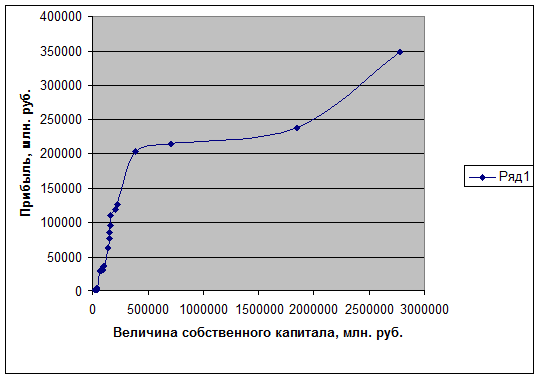
Рис. 6. Зависимость прибыли Российских предприятий от размера собственного капитала.

Заключение
Группировка – это
распределение единиц совокупности по группам в соответствии со следующим
принципом: различия между единицами, отнесенными к одной группе должны быть
меньше, чем между единицами, отнесенными к разным группам. Сводные показатели
для отдельных групп считаются устойчивыми и типичными, если они удовлетворяют
двум основным принципам:
1. Группировка должна быть
проведена правильно, для чего устанавливают правила отнесения единицы к одной
или другой группе;
2. Группы должны иметь
достаточную численность.
Обязательно, при
группировке, используют характеристику, по которой будет проводиться эта
группировка – группировочный признак. Для того чтобы отделить одну группу от
другой применяют интервалы группировки. Расчленение совокупностей единиц по
группам производятся:
1. По одному признаку, т.е.
простая группировка (монотетическая);
2. По двум или более
признакам, т.е. сложная группировка (комбинационная, политетическая).
По сравнению с простыми
комбинационные группировки обладают дополнительными аналитическими свойствами.
Признак,
по которому производится образование групп, называется группировочным признаком
или основанием группировки. Выбор ее зависит от решения конкретной задачи. Для
многих признаков разрабатываются устойчивые номенклатуры групп и подгрупп,
которые называются классификациями. Для образования групп обычно устанавливают
интервалы.
Для изучения силы (тесноты) связей между
факторными и результативными признаками исчисляют эмпирические корреляционные
отношения. Для этого надо иметь четкое представление по факторным и
результативным признакам. Если каждому значению величины факторного признака
соответствует только одно результативного признака, то такая связь между
величинами называется функциональной. Эти связи выражаются формулами и широко применяются в математике, физике,
астрономии.
В
экономических явлениях проявляется зависимость распределения значений
результативного признака от нескольких значений факторов. Такого рода связи
называются стохастическими. В частном случае стохастической является
корреляционная связь. При этой связи одному и тому же значению факторного
признака, могут соответствовать самые различные значения результативного
признака.
Список
использованной литературы:
1.
Гусаров В.М., «Теория статистики», – М.: Аудит, ЮНИТИ,
2002;
2.
Ефимова М.П., Петрова Е.В., Румянцев В.Н., «Общая
теория статистики», - М.: “Инфра - М”, 2003;
3.
«Практикум по статистике: Учеб. пособие для вузов» / Под
ред. В. М. Симчеры / ВЗФЭИ. – М.: ЗАО
«Финстатинформ», 2000;
4.
Статистика. Задания по выполнению курсовой работы. Для студентов III курса специальностей 060200 «Экономика труда», 061100
«Менеджмент организации». – М.: Вузовский учебник, 2003;
5.
Экономика и статистика фирм: Учебник./ Под ред. С.Д.
Ильенковой, - М.: Финансы и статистика, 1996;
6.
Батракова Л.Г., «Экономический анализ деятельности
коммерческих банков», - М.,
Логос, 1999;
7.
www.ecsocman.edu.ru