Федеральное агентство по образованию
ГОУ ВПО
Всероссийский заочный финансово-экономический институт
Кафедра статистики
КОНТРОЛЬНАЯ РАБОТА
по дисциплине
«СТАТИСТИКА»
Вариант №13
Исполнитель:
Специальность:
Бухгалтерский учет, анализ и аудит
Группа:
№
зачетной книжки: Преподаватель:
ПЕНЗА
2008
Вариант №13
Имеются следующие
выборочные данные по предприятиям одной из отраслей промышленности в отчетном
году (выборка 5%-ная механическая).
Выборочные данные
представлены в табл.1.
Исходные данные Таблица 1
|
Номер органи-зации
п/п
|
Среднесписочная численность работников, чел.
|
Фонд заработной платы, млн. руб.
|
Номер
органи-зации
п/п
|
Среднесписочная численность работников, чел.
|
Фонд заработной платы, млн. руб.
|
|
1
|
162
|
11,340
|
16
|
162
|
11,502
|
|
2
|
156
|
8,112
|
17
|
188
|
16,356
|
|
3
|
179
|
15,036
|
18
|
164
|
12,792
|
|
4
|
194
|
19,012
|
19
|
192
|
17,472
|
|
5
|
165
|
13,035
|
20
|
130
|
5,850
|
|
6
|
158
|
8,532
|
21
|
159
|
9,858
|
|
7
|
220
|
26,400
|
22
|
162
|
11,826
|
|
8
|
190
|
17,100
|
23
|
193
|
18,142
|
|
9
|
163
|
12,062
|
24
|
158
|
8,848
|
|
10
|
159
|
9,540
|
25
|
168
|
13,944
|
|
11
|
167
|
13,694
|
26
|
208
|
23,920
|
|
12
|
205
|
21,320
|
27
|
166
|
13,280
|
|
13
|
187
|
16,082
|
28
|
207
|
22,356
|
|
14
|
161
|
10,465
|
29
|
161
|
10,948
|
|
15
|
120
|
4,320
|
30
|
186
|
15,810
|
Задание 1
По исходным данным (табл.1):
1.
Построить статистический ряд распределения организаций
(предприятий) по признаку среднесписочная численность работников,
образовав пять групп с равными интервалами.
2.
Построить графики полученного ряда распределения.
Графически определить значения моды и
медианы.
3.
Рассчитать характеристики интервального ряда
распределения: среднюю арифметическую,
среднее квадратическое отклонение, коэффициент вариации, моду и медиану.
4.
Вычислить среднюю
арифметическую по исходным данным (табл. 1), сравнить её с аналогичным
показателем, рассчитанным в п. 3 для интервального ряда распределения.
Объяснить причину их расхождения.
Сделать
выводы по результатам выполнения задания.
Решение:
1.1. Построение статистического ряда распределения
Для построения
статистический ряд распределения необходимо вычислить величину и границы интервалов ряда.
Исходные данные представлены в таблице 2 (графа 5 этой таблицы необходима для
выполнения Задания 2).
Таблица 2
Исходные
данные
|
Номер предпр.
|
Среднесписочная численность работников, чел.
|
Фонд заработной платы, млн. руб.
|
|
Среднесписочная численность работников, чел.
|
|
1
|
2
|
3
|
|
4
|
|
1.
|
162
|
11,340
|
|
162
|
|
2.
|
156
|
8,112
|
|
156
|
|
3.
|
179
|
15,036
|
|
179
|
|
4.
|
194
|
19,012
|
|
194
|
|
5.
|
165
|
13,035
|
|
165
|
|
6.
|
158
|
8,532
|
|
158
|
|
7.
|
220
|
26,400
|
|
220
|
|
8.
|
190
|
17,100
|
|
190
|
|
9.
|
163
|
12,062
|
|
163
|
|
10.
|
159
|
9,540
|
|
159
|
|
11.
|
167
|
13,694
|
|
167
|
|
12.
|
205
|
21,320
|
|
205
|
|
13.
|
187
|
16,082
|
|
187
|
|
14.
|
161
|
10,465
|
|
161
|
|
15.
|
120
|
4,320
|
|
120
|
|
16.
|
162
|
11,502
|
|
162
|
|
17.
|
188
|
16,356
|
|
188
|
|
18.
|
164
|
12,792
|
|
164
|
|
19.
|
192
|
17,472
|
|
192
|
|
20.
|
130
|
5,850
|
|
130
|
|
21.
|
159
|
9,858
|
|
159
|
|
22.
|
162
|
11,826
|
|
162
|
|
23.
|
193
|
18,142
|
|
193
|
|
24.
|
158
|
8,848
|
|
158
|
|
25.
|
168
|
13,944
|
|
168
|
|
26.
|
208
|
23,920
|
|
208
|
|
27.
|
166
|
13,280
|
|
166
|
|
28.
|
207
|
22,356
|
|
207
|
|
29.
|
161
|
10,948
|
|
161
|
|
30.
|
186
|
15,810
|
|
186
|
|
Итого:
|
5190
|
418,954
|
|
5190
|
При построении ряда с
равными интервалами величина интервала h определяется по формуле
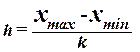 ,
(1)
,
(1)
где xmax, xmin – наибольшее и наименьшее значения признака в исследуемой
совокупности, k- число групп интервального ряда.
Определяем
величины интервала по формуле (1) при заданных
k =5, xmax
= 220 чел., xmin = 120 чел.:
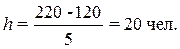
При h = 20. границы
интервалов ряда распределения имеют следующий вид (табл. 3):
Таблица
3
|
Номер группы
|
Нижняя граница,
млн руб.
|
Верхняя граница,
млн руб.
|
|
1
|
120
|
140
|
|
2
|
140
|
160
|
|
3
|
160
|
180
|
|
4
|
180
|
200
|
|
5
|
200
|
220
|
Для
построения интервального ряда необходимо подсчитать число организаций, входящих
в каждую группу (частоты групп).
Процесс группировки единиц
совокупности по признаку среднесписочная численность работников представлен во
вспомогательной (рабочей) таблице 4.
Таблица 4
Рабочая таблица для построения статистического ряда
распределения и аналитической группировки
|
Номер предпр.
|
Среднесписочная численность работников, чел.
|
Фонд заработной платы, млн. руб.
|
|
1
|
2
|
3
|
|
15
|
120
|
4,320
|
|
20
|
130
|
5,850
|
|
Итого:2
|
250
|
10,170
|
|
2.
|
156
|
8,112
|
|
6.
|
158
|
8,532
|
|
24.
|
158
|
8,848
|
|
10.
|
159
|
9,540
|
|
21.
|
159
|
9,858
|
|
Итого:5
|
790
|
44,890
|
|
29.
|
161
|
10,948
|
|
14.
|
161
|
10,465
|
|
1.
|
162
|
11,340
|
|
16.
|
162
|
11,502
|
|
22.
|
162
|
11,826
|
|
9.
|
163
|
12,062
|
|
18.
|
164
|
12,792
|
|
5.
|
165
|
13,035
|
|
27.
|
166
|
13,280
|
|
11.
|
167
|
13,694
|
|
25.
|
168
|
13,944
|
|
3.
|
179
|
15,036
|
|
Итого:12
|
1980
|
149,924
|
|
30.
|
186
|
15,810
|
|
13.
|
187
|
16,082
|
|
17.
|
188
|
16,356
|
|
8.
|
190
|
17,100
|
|
19.
|
192
|
17,472
|
|
23.
|
193
|
18,142
|
|
4.
|
194
|
19,012
|
|
Итого:7
|
1330
|
119,974
|
|
12.
|
205
|
21,320
|
|
28.
|
207
|
22,356
|
|
26.
|
208
|
23,920
|
|
7.
|
220
|
26,400
|
|
Итого:4
|
840
|
93,996
|
|
Итого:
|
5190
|
418,954
|
На основе групповых
итоговых строк «Итого» табл. 4 формируется итоговая таблица 5, представляющая
интервальный ряд распределения предприятий по среднесписочной численности
работников.
Таблица 5
Распределение предприятий по среднесписочной численности
работников
|
Номер группы
|
Группы предприятий по среднесписочной
численности работающих, чел.
|
Число предприятий
|
Накопленная
частота,
Si
|
|
1
|
2
|
3
|
4
|
|
1
|
120-140
|
2
|
2
|
|
2
|
140-160
|
5
|
7
|
|
3
|
160-180
|
12
|
19
|
|
4
|
180-200
|
7
|
26
|
|
5
|
200-220
|
4
|
30
|
|
|
Итого
|
30
|
|
Помимо частот
групп в абсолютном выражении в анализе интервальных рядов используются ещё накопленные (кумулятивные) частоты Si, получаемые путем последовательного
суммирования частот всех предшествующих (i-1)
интервалов.
Вывод. Анализ интервального ряда
распределения изучаемой совокупности предприятий показывает, что распределение
предприятий по среднесписочной численности работников не является равномерным:
преобладают организации со среднесписочной численности работников от 160 до 180
чел. (это 12 организаций, доля которых составляет 40%).
1.2. Построение графиков полученного
ряда распределения, графическое определение значений моды и медианы
Мода и медиана являются структурными
средними величинами, характеризующими центр распределения единиц
совокупности по изучаемому признаку.
Мода Мо для дискретного ряда – это значение
признака, наиболее часто встречающееся у единиц исследуемой совокупности. В
интервальном вариационном ряду модой приближенно считается центральное значение модального интервала (имеющего наибольшую
частоту). Более точно моду можно определить графическим методом по гистограмме
ряда (рис.1).
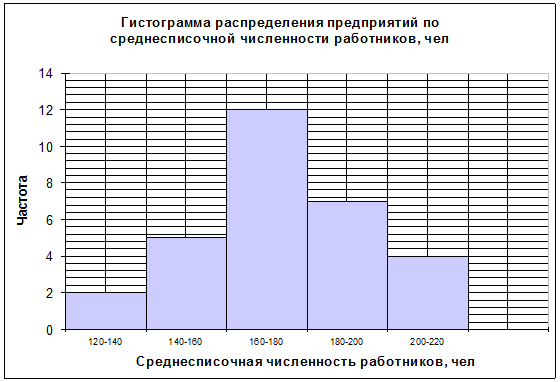
Рис. 1
Определение моды графическим методом
Медиана Ме – это значение признака, приходящееся
на середину ранжированного ряда. По обе стороны от медианы находится одинаковое
количество единиц совокупности.
Медиану можно определить графическим
методом по кумулятивной кривой (рис. 2). Кумулята строится по накопленным
частотам (табл.5, графа 4).
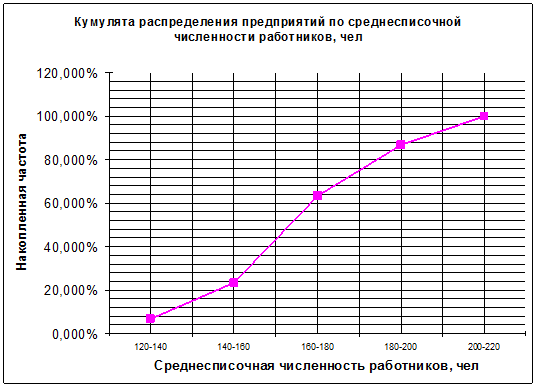
Рис. 2. Определение медианы графическим методом
1.3. Расчет характеристик интервального ряда распределения
Средняя арифметическая
взвешенная 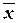 – средняя сгруппированных величин:
– средняя сгруппированных величин:
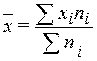 ,
(2)
,
(2)
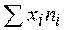 - сумма произведений величины признаков на их частоты;
- сумма произведений величины признаков на их частоты;
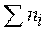 -общая численность единиц совокупности;
-общая численность единиц совокупности;
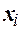 – середина i-го интервала/
– середина i-го интервала/
Среднее квадратическое отклонеие
(σ) равно корню квадратному из дисперсии. Дисперсия признака (σ2)
представляет собой средний квадрат отклонений вариантов от их средней величины
и равна разности средней из квадратов вариантов ( ) и квадрата их средней (
) и квадрата их средней (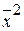 )
)
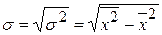 (3)
(3)
Коэффициент вариации представляет
собой выраженное в процентах отношение среднего квадратического отклонения к
средней арифметической и
характеризует однородность совокупности:
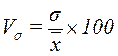 (4)
(4)
Значение моды для
интервального ряда рассчитывается по формуле:
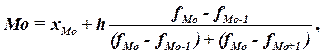 (5)
(5)
хМo – нижняя граница модального интервала,
h –величина модального интервала,
fMo – частота модального интервала,
fMo-1 – частота интервала, предшествующего
модальному,
fMo+1 – частота интервала, следующего за модальным.
Значение медианы для
интервального ряда рассчитывается по
формуле:
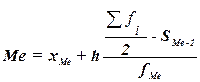 (6)
(6)
где
хМе– нижняя граница медианного интервала,
h – величина медианного интервала,
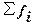 – сумма всех частот,
– сумма всех частот,
fМе – частота медианного интервала,
SMе-1 – накопленная частота предмедианного
интервала.
Для расчета медианы
необходимо, определить медианный интервал, для чего используются накопленные
частоты из табл. 5 (графа 5). Так как медиана делит численность ряда пополам,
она будет располагаться в том интервале, где накопленная частота впервые
равна полусумме всех частот 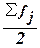 или превышает ее.
или превышает ее.
Медианным является
интервал 160 – 180 чел.
Для расчета характеристик
ряда распределения с помощью Microsoft Exel строится расчетная таблица 6 (в
таблице 7 расчет представлен в режиме отображения формул).
Выводы. Анализ полученных значений показателей средней арифметической взвешенной
(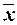 ) и среднего квадратического отклонения (σ) говорит о том, что среднесписочная
численность работников составляет 173 чел., отклонение от среднего объема в ту
или иную сторону составляет в среднем 21 чел. (или 12,4%).
) и среднего квадратического отклонения (σ) говорит о том, что среднесписочная
численность работников составляет 173 чел., отклонение от среднего объема в ту
или иную сторону составляет в среднем 21 чел. (или 12,4%).
Значение коэффициента
вариации V = 12,4% не превышает 33%,
следовательно, вариация среднесписочная численность работников в исследуемой
совокупности организаций незначительна и совокупность по данному признаку
качественно однородна.
Мода свидетельствует, что
для рассматриваемой совокупности организаций наиболее распространенная величина
среднесписочной численности работников характеризуется средней величиной 172
чел
Медиана показывает, что
из 30 организаций 15 организаций имеют среднесписочную численность работников менее
173 чел, а 15 организаций – более.
Расхождение между
значениями 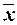 , Мо и Ме незначительно (
, Мо и Ме незначительно (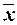 =174чел, Мо=172 чел., Ме=173 чел.), следовательно
распределение близко к нормальному.
=174чел, Мо=172 чел., Ме=173 чел.), следовательно
распределение близко к нормальному.
1.4. Вычисление средней арифметической по исходным данным
Для расчета
применяется формула средней арифметической простой:
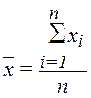 (7)
(7)
Причина
расхождения средних величин, рассчитанных по формулам (2) и (7), заключается в
том, что по формуле (7) средняя определяется по фактическим значениям
исследуемого признака для
всех 30-ти организаций, а по
формуле (2) средняя вычисляется для интервального ряда, когда в качестве
значений признака берутся середины интервалов xi
, что приводит к погрешности.
Задание 2
По исходным данным:
1.
Установить наличие и характер связи между признаками среднесписочная численность работников и
фонд заработной платы, образовав пять
групп по обоим признакам с равными интервалами, используя методы:
а)
аналитической группировки;
б)
корреляционной таблицы.
2.
Измерить тесноту корреляционной связи между признаками
с использованием коэффициента
детерминации и эмпирического корреляционного отношения.
Сделать
выводы по результатам выполнения задания .
Решение:
2.1. Установление наличия и характера
связи между признаками
1а. Применение метода
аналитической группировки
При использовании метода
аналитической группировки строится интервальный ряд распределения единиц
совокупности по факторному признаку Х
и для каждой i-ой
группы ряда определяется среднегрупповое значение 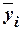 результативного признака Y. Если с
ростом значений фактора Х от группы
к группе средние значения
результативного признака Y. Если с
ростом значений фактора Х от группы
к группе средние значения 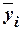 систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
Используя
разработочную таблицу 4, строим аналитическую группировку, характеризующую
зависимость между факторным признаком Х
– среднесписочная численность
работников и результативным признаком Y – фонд заработной платы.
Групповые средние значения 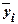 получаем из
таблицы 4 (графа 5), основываясь на итоговых
строках «Всего». Построенная аналитическая
группировка представлена в таблице 8 (в таблице 9 представлен режим отображения
формул).
получаем из
таблицы 4 (графа 5), основываясь на итоговых
строках «Всего». Построенная аналитическая
группировка представлена в таблице 8 (в таблице 9 представлен режим отображения
формул).
Из таблицы 8 видно, что с
увеличением среднесписочой численности работников возрастает фонд заработной
платы, что свидетельствует о наличии прямой корреляционной связи между
исследуемыми признаками.
|
|
|
|
|
|
Таблица 8
|
|
Аналитическая
таблица
|
|
|
|
|
|
|
|
|
|
|
|
|
Группы предприятий по среднесписочной численности,
чел.
|
число предприятий
|
Среднесписочная численность работающих, чел.
|
Фонд заработной платы, млн. руб.
|
|
Всего
|
В среднем на 1 предпр.
|
Всего
|
В среднем на 1 предпр.
|
|
120-140
|
2
|
250
|
125,0
|
10,17
|
5,1
|
|
140-160
|
5
|
790
|
158,0
|
44,89
|
9,0
|
|
160-180
|
12
|
1980
|
165,0
|
149,924
|
12,5
|
|
180-200
|
7
|
1330
|
190,0
|
119,974
|
17,1
|
|
200-220
|
4
|
840
|
210,0
|
93,996
|
23,5
|
|
Итого:
|
30
|
5190
|
173,0
|
418,954
|
14,0
|
|
|
|
|
|
|
|
|
С
увеличением среднесписочной численности работающих в среднем на одно
предприятие
|
|
фонд
заработной платы в среднем на одно предприятие также растет
|
|
|
|
|
|
|
|
Таблица 9
|
|
|
Аналитическая
таблица в режиме отображения формул
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Группы предприятий по среднесписочной численности,
чел.
|
число предприятий
|
Среднесписочная численность работающих, чел.
|
Фонд заработной платы, млн. руб.
|
|
Всего
|
В среднем на 1 предпр.
|
Всего
|
В среднем на 1 предпр.
|
|
120-140
|
2
|
250
|
=C6/B6
|
10,17
|
=E6/B6
|
|
140-160
|
5
|
790
|
=C7/B7
|
44,89
|
=E7/B7
|
|
160-180
|
12
|
1980
|
=C8/B8
|
149,924
|
=E8/B8
|
|
180-200
|
7
|
1330
|
=C9/B9
|
119,974
|
=E9/B9
|
|
200-220
|
4
|
840
|
=C10/B10
|
93,996
|
=E10/B10
|
|
Итого:
|
=СУММ(B6:B10)
|
=СУММ(C6:C10)
|
=C11/B11
|
=СУММ(E6:E10)
|
=E11/B11
|
|
|
|
|
|
|
Таблица 10
|
|
Величина
интервала результативного признака
|
Миним.
значение результативного признака
|
Макс.
значение результативного признака
|
|
|
|
|
|
4,416
|
4,320
|
26,400
|
|
|
|
|
|
Корреляционная таблица
|
|
|
|
|
|
|
|
|
|
Группы предприятий по среднесписочной численности,
чел.
|
Фонд заработной платы, млн. руб.
|
|
4,320-8,736
|
8,736-13,152
|
13,152-17,568
|
17,568-21,984
|
21,984-26,400
|
Итого
|
|
120-140
|
2
|
|
|
|
|
2
|
|
140-160
|
2
|
3
|
|
|
|
5
|
|
160-180
|
|
8
|
4
|
|
|
12
|
|
180-200
|
|
|
5
|
2
|
|
7
|
|
200-220
|
|
|
|
1
|
3
|
4
|
|
Итого:
|
4
|
11
|
9
|
3
|
3
|
30
|
|
|
|
|
|
|
|
|
|
Т.к.
частоты признака рассеяны вдоль главной диагонали,
|
|
|
|
|
связь
между признаками среднесписочная численность и
|
|
|
|
|
фонд
заработной платы тесная, прямая
|
|
|
|
|
1б. Применение метода
корреляционной таблицы.
Корреляционная таблица
представляет собой комбинацию двух рядов распределения. Строки таблицы
соответствуют группировке единиц совокупности по факторному признаку Х, а графы – группировке единиц по
результативному признаку Y. На пересечении i-ой строки и k-ой графы указывается число единиц
совокупности, входящих в i-ый интервал по факторному признаку и
в k-ый
интервал по результативному признаку. Концентрация частот около диагонали
построенной таблицы свидетельствует о наличии корреляционной связи между
признаками.
Для построения
корреляционной таблицы необходимо знать величины и границы интервалов по двум
признакам X и Y. Величина интервала и границы интервалов для
факторного признака Х
– среднесписочная численность работников известны.
Для результативного признака Y – фонд заработной платы величина интервала
определяется по формуле (1) при k = 5, уmax = 26,4 млн. руб., уmin = 4,32 млн. руб.:
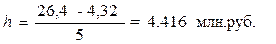
Используя группировки по
факторному и результативному признакам, строим корреляционную таблицу (табл.
10).
Вывод. Анализ данных табл. 10 показывает, что распределение частот групп
произошло вдоль диагонали, идущей из левого верхнего угла в правый нижний угол
таблицы. Это свидетельствует о наличии прямой корреляционной связи между признаками
среднесписочная численность и фонд заработной платы.
2.2. Измерение тесноты корреляционной связи
Для измерения тесноты
связи между факторным и результативным признаками рассчитывают специальные
показатели – эмпирический коэффициент детерминации η2 и эмпирическое корреляционное
отношение η.
Эмпирический коэффициент детерминации η2 оценивает, насколько вариация
результативного признака Y
объясняется вариацией фактора Х.
Показатель η2 рассчитывается как доля межгрупповой дисперсии в
общей дисперсии по формуле
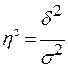 ,
(9)
,
(9)
где
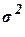 – общая дисперсия
признака Y,
– общая дисперсия
признака Y,
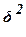 – межгрупповая
(факторная) дисперсия признака Y.
– межгрупповая
(факторная) дисперсия признака Y.
Значения показателя η2
изменяются в пределах
0≤
η2 ≤1. При
отсутствии корреляционной связи между признаками Х
и Y имеет место равенство η2
=0, а при наличии функциональной связи между ними – равенство η2 =1.
Общая
дисперсия σ2 характеризует
вариацию результативного признака, сложившуюся под влиянием всех действующих на
Y факторов
(систематических и случайных).
Общая дисперсия может
быть рассчитана по формуле
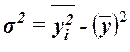 ,
,
где 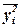 – средняя из квадратов значений
результативного признака,
– средняя из квадратов значений
результативного признака,
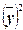 – квадрат средней величины значений
результативного признака.
– квадрат средней величины значений
результативного признака.
Межгрупповая дисперсия
δ2 измеряет
систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х
(по которому произведена группировка). Воздействие фактора Х на результативный признак Y
проявляется в отклонении групповых средних 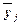 от
общей средней
от
общей средней 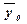 . Показатель δ2
вычисляется по формуле
. Показатель δ2
вычисляется по формуле
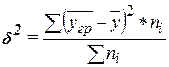 , (13)
, (13)
где
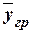 – групповые
средние,
– групповые
средние,
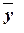 – общая
средняя,
– общая
средняя,
ni
–число единиц в i-ой
группе,
Расчет эмпирического коэффициента
детерминации η2
по формуле (9):
Эмпирическое
корреляционное отношение η оценивает тесноту связи
между факторным и результативным признаками и вычисляется по формуле
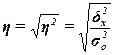 (14)
(14)
Значение показателя изменяются в пределах
0≤ η ≤1. Чем ближе значение η к 1, тем теснее связь между
признаками. Для качественной оценки тесноты связи на основе η служит шкала
Чэддока.
Для расчетов строятся вспомогательные таблицы
11,12, в таблицах 13,14 расчеты представлены в режиме отображения формул.
Вывод. Эмпирический коэффициент
детерминации η2
показывает, что 94,1% вариации среднесписочной численности работников
обусловлено вариацией фонда заработной платы, а 5,9% – влиянием прочих неучтенных факторов.
Значение
корреляционного отношения η близко к 1. Согласно шкале Чэддока, связь
между среднесписочной численности работников и фонда заработной платы является
тесной, так как η=0,970.
Задание 3
По результатам выполнения Задания
1 с вероятностью 0,954 определить:
1)
ошибку выборки среднесписочной численности работников и
границы, в которых будет находиться средняя в генеральной совокупности.
2)
ошибку выборки доли организаций со среднесписочной
численностью работников 100 и более человек и границы, в которых будет
находиться генеральная доля.
Решение:
3.1. Определение ошибки выборки.
Предельная ошибка выборки позволяет
определить предельные значения характеристик генеральной совокупности и их
интервалы
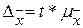
Средняя ошибка выборки в случае
бесповторного отбора для средней вычисляется по формуле:
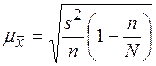 ,
,
s2– дисперсия выборочной совокупности;
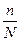 − доля выборки. Так как по условию выборка 5%-ная, то
− доля выборки. Так как по условию выборка 5%-ная, то 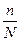 =0,05
=0,05
Тогда предельная ошибка выборки для
средней будет равна:
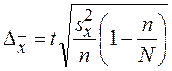
Так как по условию ошибку
надо гарантировать с вероятностью 0,954, то коэффициент доверия t=2. Из расчетов задачи 1 дисперсия равна s2=σ2=21,542 =463,97
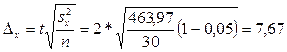 (чел.)
(чел.)
Тогда
границы, в которых будет находиться среднесписочной
численности работников: 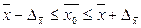 ;
; 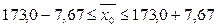 ;
; 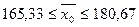
Вывод. На
основании проведенного выборочного обследования с вероятностью 0,954 в
генеральной совокупности организаций среднесписочная численность работников находится
в пределах от 165,33 чел. до 180,67 чел.
3.2. Определение ошибки выборки доли организаций
Выборочная доля организаций со среднесписочной
численностью работников 180 и более чел. и более равна:
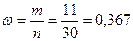
где
m – число единиц совокупности,
обладающих заданным свойством;
n – общее число единиц в совокупности.
Найдем предельную ошибку выборки для
доли Δω в случае бесповторного отбора:
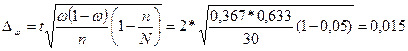
где ω – доля
единиц совокупности, обладающих заданным свойством;
(1-ω) – доля
единиц совокупности, не обладающих заданным свойством,
N – число
единиц в генеральной совокупности,
n– число
единиц в выборочной совокупности.
Тогда границы, в которых
будет находиться генеральная доля предприятий со среднесписочной численностью
работников 180 и более чел. равна:
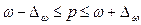 ;
; 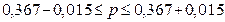 ;
; 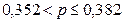
Вывод. С вероятностью 0,954 можно утверждать, что в
генеральной совокупности организаций доля организаций со среднесписочной
численностью работников 180 и более чел., будет находиться в пределах от 35% до
38%.
Задание 4
Имеются следующие данные по двум организациям:
|
№ организации п/п
|
Базисный период
|
Отчетный
период
|
|
Средняя
заработная плата, руб.
|
Среднесписочная численность работников, чел.
|
Средняя заработная плата, руб.
|
Фонд заработной
платы, тыс. руб.
|
Среднесписочная численность работников, чел
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
5000
|
100
|
6500
|
682,5
|
105
|
|
2
|
5600
|
100
|
8000
|
760,0
|
95
|
Определите:
1. Индексы
динамики средней заработной платы по каждой организации.
Результаты расчетов
представьте в таблице.
2. По двум организациям вместе:
- индексы средней
заработной платы переменного, постоянного состава, структурных сдвигов;
- абсолютное изменение
средней заработной платы в целом и за счет отдельных факторов;
- абсолютное изменение
фонда заработной платы вследствие
изменения среднесписочной численности работников,
средней заработной платы и двух факторов вместе.
Сделайте выводы.
Решение:
Расчеты представлены в таблице 15.
Таблица 15
|
№ организации п/п
|
Базисный период
|
Отчетный период
|
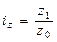
Индивид. индексы средней
заработ. платы
|
Фонд заработной платы, тыс. руб.
|
|
Базисн
|
Отчетн.
|
Базисные в пересчете на факт. числ-ть
|
|
Средняя заработная плата, руб.
(z0)
|
Среднесписочная численность
работников, чел. (q0)
|
Средняя заработная плата, руб.
(z1)
|
Фонд заработной платы, тыс. руб.
|
Среднесписочная численность
работников, чел; (q1)
|
z0q0
|
z1q1
|
z0q1
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
|
|
|
|
1
|
5000
|
100
|
6500
|
682,50
|
105
|
1,300
|
500,00
|
682,50
|
525,00
|
|
2
|
5600
|
100
|
8000
|
760,00
|
95
|
1,429
|
560,00
|
760,00
|
532,00
|
Индекс переменного
состава будет равен
Таким образом, по двум
предприятиям средняя заработная плата увеличилась на 36,1%, в то время как
увеличение средней заработной платы по первому предприятию 30%, а по второму
42,9%.
Причина такого
расхождения кроется в сущности индекса. Индекс переменного состава
характеризует изменение средней заработной платы (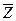 ). На величине средней каждого периода отражается не только
изменение средней заработной платы, но и изменение удельного веса каждого
предприятия в общем фонде оплаты труда. Следовательно, на индексе переменного
состава сказывается влияние сразу двух факторов. Для того, чтобы выявить
влияние каждого фактора в отдельности на величину индекса переменного состава,
следует рассчитать еще 2 индекса: индекс постоянного (фиксированного) состава и
индекс структурных сдвигов.
). На величине средней каждого периода отражается не только
изменение средней заработной платы, но и изменение удельного веса каждого
предприятия в общем фонде оплаты труда. Следовательно, на индексе переменного
состава сказывается влияние сразу двух факторов. Для того, чтобы выявить
влияние каждого фактора в отдельности на величину индекса переменного состава,
следует рассчитать еще 2 индекса: индекс постоянного (фиксированного) состава и
индекс структурных сдвигов.
Индекс постоянного
(фиксированного) состава - это тоже отношение двух средних средней заработной платы, но при
условии неизменной структуры (удельного веса предприятий в общем фонде оплаты
труда).
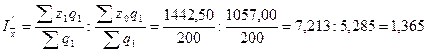 или 36,5%.
или 36,5%.
Этот индекс учитывает
изменение только самой средней заработной платы; без перераспределения
работников по предприятиям: она увеличилась бы на 36,5%.
Для выявления влияния
структурных сдвигов рассчитываем индекс структурных сдвигов. Это тоже
отношение двух средних уровней средней заработной платы, но в них исключено
влияние средней заработной платы:
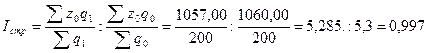 или 99,7%.
или 99,7%.
Следовательно, в
результате перераспределения в числе работников по предприятиям, а именно,
уменьшения их количества на втором предприятии с более высокой средней
заработной платой и увеличения на первом, где средняя заработная плата
меньше, произошло незначительное
снижение уровня средней заработной платы
на 0,3%.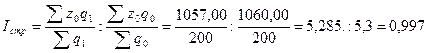
Взаимосвязь этих индексов: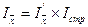 . В
приведенном примере 1,361=1,365*0,997.
. В
приведенном примере 1,361=1,365*0,997.
В абсолютных величинах:
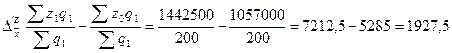 руб.
руб.
На 1927,5 руб. увеличивается средняя заработная плата под
влиянием самой индексируемой величины ( т.е. средней зар.платы ).
 руб.
руб.
На 15 руб. уменьшается средняя заработная плата за счет
изменения среднесписочной численности.
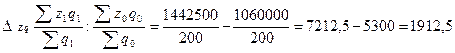 руб.
руб.
На 1912,5руб. уменьшается средняя заработная плата под
влиянием двух вышеназванных факторов
Взаимосвязь и разложение абсолютного прироста по факторам
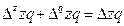 т.е, 1927,5-15=1912,5
т.е, 1927,5-15=1912,5
Список использованной литературы;
1.
Гусаров В.М. Статистика: Учеб пособие для вузов. — М.:
ЮНИТИ-ДАНА, 2004. – 463 с.
2.
Практикум по статистике: Учеб. пособие для вузов/ Под
ред. В.М. Симчеры / ФЗФЭИ. — М.: ЗАО «Финстатинформ», 1999. – 259 с.
3.
Статистика. Методические рекомендации к выполнению
статистических расчётов курсовых, контрольных и выпускных квалификационных
работ. Часть I. Комплексное использование методов при проведении
статистического анализа данных. Для студентов всех специальностей (первое и
второе высшее образование).– М.:ВЗФЭИ, 2007.– 41с.
Таблица 15
|
№ организации п/п
|
Базисный период
|
Отчетный период
|
|
Индивид. индексы средней заработ. платы
|
|
|
|
Фонд заработной платы, тыс. руб.
|
|
Базисн
|
Отчетн.
|
Базисные в пересчете на фактич. числ-ть
|
|
Средняя заработная плата, руб.
(z0)
|
Среднесписочная численность
работников, чел. (q0)
|
Средняя заработная плата, руб.
(z1)
|
Фонд заработной платы, тыс. руб.
|
Среднесписочная численность
работников, чел; (q1)
|
z0q0
|
z1q1
|
z0q1
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
5000
|
100
|
6500
|
682,50
|
105
|
1,300
|
500,00
|
682,50
|
525,00
|
|
2
|
5600
|
100
|
8000
|
760,00
|
95
|
1,429
|
560,00
|
760,00
|
532,00
|