2.Тип эконометрических данных используемых в
эконометрических исследованиях
Эконометрика - это наука, ɣ позволяет осуществить количественное выражение
взаимосвязей экономических явлений.
Для оценки кол-ого
выражения необходимо построить эконометрическую модель.
Все переменные
эконометрической модели делят на экзогенные, эндогенные и предопреленные.
Экзогенные – это переменные, ɣ входят в модель, но задаются как бы из вне, т.е. так
называемые независимые переменные.
Эндогенные – определяются
самим явлением, для ɣ строится модель.
///В модели они явл предметом объяснения, т.е. зависимости (объясняемыми)
переменными. ///
Предопределенными называются переменных выступающие в системе в
роли аргументов или так наз объясняющими переменными.
Т.е. множество предопределенных переменных состоит из множества экзогенных
переменных и так наз лаговых эндогенных переменных.
Лаговые эндогенные - это такие переменных, значение γ входят в изучаемую систему будучи оценены в прошлых
периодах .
/// Иначе, в настоящей момент
времени мы их считаем известными, заданными переменными. ///
3.Статистическая зависимость (независимых случайных
переменных) ковариация
Статистическая зависимость м\у двумя переменными - каждому значению (одному) у
соответствует не одно, а множество значений или ряд распределения х.
В силу неоднозначности
статистической зависимости между у и х . Особый
интерес представляет собой усредненная по х
зависимость, и т.е. закономерность в изменении признаковых средних х, а точнее условного мат ожидания (у в зависимости от х)
Мч(у) - Т.е. получим корреляционную зависимость.
Наличие корреляционной
зависимости не может ответить на вопрос о причине связи. Корреляция
устанавливает лишь меру этой связи, т.е. меру согласованного варьирования.
Меру взаимосвязи м\у 2 мя переменными
можно найти с помощью ковариации.
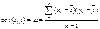 ,
, 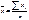 ,
, 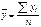
Величина показателя ковариации
зависит от единиц в γ измеряется переменная. Поэтому для оценки степени согласованного
варьирования используют коэффициент корреляции – безразмерную характеристику
имеющую определенный пределы варьирования..
Основными числовыми
характеристиками меры связи м\у переменными явл: парные кофэ-ы корреляции,
частные коэф-ы корреляции и множественные коэф-ы корреляции.
/// Последние 2 имеют место
если переменных больше 2. ///
Для 2х переменных парный
коэффициент корреляции определяется по формуле: 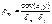 , где
, где 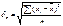 ;
; 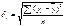 .
.
5.Основные этапы построения эконометрических моделей
На первом постановочном этапе
построения эконометрической модели формируются цели моделирования, определяется
набор участвующих в модели факторов, т.е. устанавливается, какие из переменных
будут рассматриваться как экзогенные, а какие как эндогенные и лаговые.
Пусть У ={у1 у2 …уm}, множество эндогенных переменных ; Х = {х1 х2 …хm} – множество экзогенных переменных.
Задачей экзогенного
моделирования является получение каждой эндогенной переменной от совокупности
экзогенных переменных и возможно от части эндогенных.
y1 = f
(x1 … xk у2 … уm)
При этом зависимые переменных
лаговые.
На 1 ом
этапе осуществляется анализ экономической сущности изучаемой модели.
На 3 ем этапе выбор общего
вида модели: парная, множественная; сколько должно войти факторов; линейная не
линейная; а так же определение коэффициентов функции f.
4 ый
этап отбор необходимой статистической информации и предварительный анализ
данных.
5 ый
этап – идентификация модели, т.е. стат анализ модели,
стат оценка независимых параметров модели. Наиболее
часто для оценки (нахождения) параметров модели применяют метод наименьших
квадратов (МНК)
6 ой этап – сопоставление
реальных и модельных значений. Иначе оценка адекватности и точности модели.
По точной и адекватной модели
осуществляется прогнозирование.
4.Анализ линейной статистической связи. Вычисление
коэффициента корреляции
Основными числовыми
характеристиками меры связи м\у переменными явл: парные кофэ-ы корреляции,
частные коэф-ы корреляции и множественные коэф-ы корреляции.
/// Последние 2 имеют место
если переменных больше 2. /// Для 2х переменных парный коэффициент корреляции
определяется по формуле:
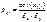 , где
, где 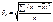 ;
; 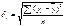 .
.
Он является показателем
тесноты связи лишь в случае линейной зависимости.
Его свойства:
1) 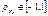
2) 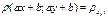 - кожф-т корреляции не зависит от выбора начала отсчета
- кожф-т корреляции не зависит от выбора начала отсчета
коэф-т корреляции величина безразмерная
если 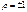 , то это
свидетельствует о функциональной зависимости м\у х и у., Если ρ=0, то связи
нет. Если
, то это
свидетельствует о функциональной зависимости м\у х и у., Если ρ=0, то связи
нет. Если 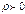 , то это
свидетельствует о положительном направлении связи, т.е. с ростом одной переменной
2-я так же возрастает, если
, то это
свидетельствует о положительном направлении связи, т.е. с ростом одной переменной
2-я так же возрастает, если 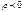 ,
направление отрицательное, т.е. с возрастанием одной переменной другая убывает.
,
направление отрицательное, т.е. с возрастанием одной переменной другая убывает.
В практических расчетах
генеральный коэффициент корреляции ρ не
известен, его оценивают по результатам выборочного исследования. Точечная
оценка ρ, иначе выборочный коэффициент корреляции:
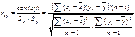 .
.
Для оценки сущ-ти
(значимости) коэффициента корреляции ρ
(генерального) применяется коэффициент t-статистики. Значение этого критерия tраспр = tнабл определяется по
формуле: 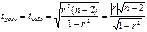
Значение вычисленной
t-статистики сравнивается с табличным, т.е. критическим значением t. Критическое значение t берется
на заданном уровне значимости α и числе степеней
свободы n-2/
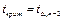
Выдвигается нулевая гипотеза
Н0, что коэф-т корреляции равен нулю. Н0 ρ =0. Вычисляется t расч, сравнивается с tкрит. Если t расч > t
крит, то гипотеза Н0 отклоняется, и принимается
противоположная гипотеза, т.е. ρ≠0. Если t расч ≤ tкрит, то гипотеза принимается. Как видно из формулы t набл, это t-статистика определяется выборочным коэф-м корреляции и числом наблюдений n,
поэтому не трудно для заданного числа степени свободы найти наименьшее значение
выборочного коэф-та r, при γ гипотеза Н0 будет отклонена к заданной доверительной
вероятностью.
6.Линейная модель парной регрессии. Оценка параметров
модели с помощью МНК
Линейная модель парной
регрессии есть: у=bх+a+e
b - коэф-т
регрессии, показывающий, как изменится у при изменении х
на единицу
a - это свободный член,
расчетная величина, содержания нет.
e - это остаточная
компонента, т.е. случайная величина, независимая, нормально распределенная, мат
ожид = 0 и постоянной дисперсией.
Присутствие e в модели свидетельствует о том, что функциональной
зависимости м\у у и х нет.
На изменение у оказывает влияние не только фактор х,
но и какие-то др не учтенные моделью факторы.
Первой задачей регрессионного
анализа явл получение значения параметров a и b. Найт этои параметры
мы не можем (пришлось бы обследовать ген совокупность), поэтому находим
выборочные оценки этих параметров.
ŷ = a + b
x
Для нахождения выборочных оценок
используем метод НК
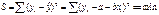
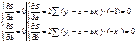
решением системы нормальных
уравнений будет:
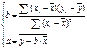
выборочные оценки для ур-я (1)
очевидно, что мин регрессия
будет иметь место только в том случае, если 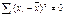 , если хi совпадает с
, если хi совпадает с 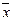 .
.
В этом случае зависимость
отсутствует.

7.Оценка существенности (значимости)
параметров линейной регрессии
Проведем оценку качества построенной моедли:
А) оценим значимость уравнения регрессии, иначе ответим
на вопрос, соответствует построенная математическая модель фактическим данным и
достаточна ли выкюч в уравнение х-фактроров
для объяснения изменения результативного показателя.
Для проверки значимости модели уравнения регрессии
используется F-критерий Фишера по γ вычисляется
F расчетное.
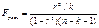 ,
,
Fрасч сравнивается с F крит с 2-я
степенями свободы: υ1 = n-1,
υ2 = n-k-1, где k - кол-во оцениваемых параметров. /k=1/
Если Fрасч > с F крит, то уравнение считается значимым, в противном случае ур-ие не значимо.
Надежность получаемых оценок а и b
зависит от ошибки ε.
Нужно найти среднюю квадратическую
ошибку 
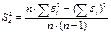 , где
, где 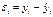
Для значимого ур-я регрессии
строят интервальные оценки параметров a и b.
Интервальная оценка параметра a,
есть:
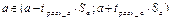
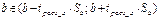
Замечание: если интервальные границы в разные по знаку,
то такие уравнения в прогнозировании использовать нельзя, т.е. непонятно какое
направление.
8.Оценка параметров множественной регрессии МНК
Линейная модель множественной
регрессии. У=а0+а1х1+ а2х2+…+ аmхm+e
Параметры определяются с
помощью методов наименьших квадратов.
Для этого проведем все рассуждения в матричной
форме. Введем следующие матричные обозначения:
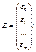
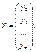

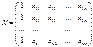 ;
; 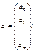
где У вектор n значений результативного показателя.
Х – матрица n значений m независимых переменных;
а матрица параметров
У=Х∙а+ε.
Заметим, что а – выборочные
оценки совокупности.
Итак, метод наименьших
квадратов требует мин-ии суммы квадратов отклонений
исходных модели значений
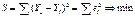 ,
, 
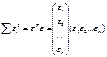
Далее: 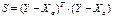
Из матричной алгебры известно,
что 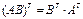 , тогда:
, тогда:
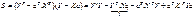
1 – это есть матрица
размерностью 1Х1, т.е. число-скаляр, а скаляр при трансформировании не меняется,
поэтому 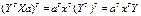 Þ
Þ 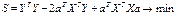
Согласно условию экстремума S
по а =0
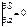 ;
; 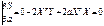
2ХТY+2aXTX=0
XTY=aXTX
Для погашения а умножим обе
части этого уравнения на (ХТХ)-1, тогда
а= (XTХ)-1∙XTY
Решение задачи нахождения
матицы, а возможно лишь в том случае, если строки и столбцы матрицы Х линейно
независимы.
9.Модель множественной регрессии. Технология разработки
прогнозов на ПВМ.
Связь между у и независимыми
факторами х1, х2, … хn можно охарактеризовать
уравнением (моделью) множественной регрессии.
Y=f (х1, х2, … хn).
Эта модель показывает, какие
значения в ср принимает результативный показатель У, если переменные Хi примут какие-то свой конкретные значения.
В зависимости от функции f будем иметь линейную или не линейную множественную
регрессию.
Тинтером было доказано, что усложнение формы связи м\у хi и у не принципиально
влияет на конечные результаты.
Линейная модель множественной
регрессии.
У=а0+а1х1+ а2х2+…+ аmхm+e
Параметры определяются с
помощью методов наименьших квадратов.
Технология разработки
прогнозов на ПВМ.
10. Регрессионные модели с переменной структурой
(фиктивные переменные).
При построении регрессионного уравнения используются
факторы, являющиеся количественными характеристиками. Иногда требуется ввести
в модель регрессии некий качественный
фактор. Это могут быть разного рода атрибутивные признаки (пол, образование,
принадлежность к какому-либо региону и т.д.). чтобы ввести такие переменные в
уравнение, их нужно преобразовать в количественные. Пусть у – цена квартиры, х - общая площадь квартиры, тогда общий вид регрессионного
уравнения примет вид, у=а0+а1х. Сконструируем фиктивную переменную, означающую
принадлежность квартиры к центральным или периферическим частям города.  . Тогда
получается уравнение 2-ухфакторной регрессии: y=a0+a1x+a2z. В этом уравнении
параметр а2 показывает, на сколько дороже квартира в центре по сравнению с
периферией города
. Тогда
получается уравнение 2-ухфакторной регрессии: y=a0+a1x+a2z. В этом уравнении
параметр а2 показывает, на сколько дороже квартира в центре по сравнению с
периферией города
11.Многомерный
статистический анализ, задачи классификации объектов. Кластерный и дискременантный анализ.
В стат
исследованиях группировка первичных данных является основным кные) задача может быть решена методами кластерного
анализа, решение отличаются от дв методов многомерной классификации отсутствием обучающих
выборок, т.е. ?апрорной? информации о распределении
ген совокупности (вектора Х)
Различие между схемами задач
по классификации определяется тем, что понимает по словом сходство и степень
сходства. После того, как сформулирована цель работы нужно определить критерии
качества, целевую функцию, значения γ позволяют
сопоставить различные схемы классификаций. В эконометрическом исследовании
целевая функция, как правило, должна минимизировать некоторые параметры
определенные на множестве объектов (например, при классификации
оборудования цель – группировка по мин
совокупных затрат вр и средств не ремонтные работы).
Если формировать цель не удается, критерием качества классификации является
возможность сосредоточительной интерпретации
найденных групп.
А) Кластерный анализ - это совокупность методов, позволяющих классифицировать
м6ногомерные наблюдения, каждое из кот описывается набором признаков
(параметров) Х1, Х2, … Хк. Целью кластерного анализа явл образование групп схожих м/у собой объектов, кот
принято называть кластерами.
Кластерный анализ – одно из
направлений статистического исследования. Особо важное место он занимает в тех
отраслях науки, γ которые связаны с изучением массовых явлений и
процессов. Необходимость развития методов кластерного анализа и их
использования продиктована тем, что они помогают построить научно обоснованные
классификации, выявить внутренние связи
м/у единицами наблюдений совокупности. Метод кластерного анализа позволяет
решить следующие задачи: проведение классификации объектов с учетом признаков,
отражающих сущность, природу объектов. Решение такой задачи, как правило,
приводит к углублению знаний о совокупности классифицируемых объектов; проверка
выдвигаемых предположений о наличии некоторой структуры в изучаемой совокупности
объектов, т.е. поиск существующей структуры; построение новых классификаций для
слабоизученных явлений. Когда необходимо установить наличие связей внутри
совокупности и попытаться привнести в нее структуру.
Обычная форма представления
исходных данных в задачах кластерного анализа прямоугольная таблица:
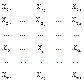 каждая строка γ
представляет собой результат измерений k рассматриваемого
признака, на одном из исследуемых объектах.
каждая строка γ
представляет собой результат измерений k рассматриваемого
признака, на одном из исследуемых объектах.
В некоторых случаях может
представлять интерес как группировка объектов, так и группировка признаков.
Матрицы не единственный способ
представления данных для задачи кластерного анализа. Иногда исходная информация
данная квадратной матрицы: R=(rij), где элемент rij определяет степень близости объекта i
к объекту j .
Выбор меры близости явл одним из условных моментов
исследования. Это может быть обыное эфклидовое расстояние (расстояние м\у
двумя точками – сумма квадратов разности одномерных координат)
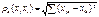 , где xik или xjk - величина k-ой компоненты у i- ого (j-ого) объекта.
, где xik или xjk - величина k-ой компоненты у i- ого (j-ого) объекта.
Б) Дискриминантный
анализ явл
разделом многомерного статистического анализа, который влк
в себя методы классификации многомерных наблюдений по принципу максимального
сходства при наличии обобщающих признаков. В Д.а. новые кластеры не образуются,
а формулируются правило, по кот объекты подмножества подлежащего классификации
относятся к одному из уже существующих (обучающих) подмножеств (классов)., на
основе сравнения величины дискриминантной функции
классифицируемого объекта, рассчитанной по дискриминантным
переменным, с некоторой константой дискриминациии.
Постановка задачи дискриминантного анализа. Пусть имеется множество М единиц
N объектов наблюдения, каждая i-ая единица кот
описывается совокупностью р значений дискириминантных переменных (признаков) xij
(i=1, 2, …, N; j =1, 2, …, p).
Причем все множество М объектов включает
q обучающих подмножеств (q≥2) Mk размером nk каждое и
подмножество М0 объектов подлежащих дискриминации (под дискриминацией
понимается различие). Здесь – номер подмножества (класса), k=1, 2, …,q.
Требуется установить правило
(линейную или не линейную дискриминантную функцию) f(X)) распределения m-объектов подмножества М0 по подмножествам
Мk
Наиболее часто используется
линейная форма дискриминантной функции, которая
представляется в виде скалярного произведения векторов А=(а1, а2, …, ар) дискриминантных множителей и вектора Хi=(xi1,
xi2, …xip) дискриминантных
переменных: Fi=A x X`i или
Fi=a1xi,1+a2xi,2+…+apxi,p (хij
– значегие j-x признаков у i –гог объекта наблюдения. Дискриминантный анализ проводится в условиях следующих
основных предположений: 1) множество М объектов Мк
(класса), кот отличаются от других групп переменными хij
, 2) в каждом подмножестве Мк находятся, по крайней
мере, два объекта (nk≥2) не менее чем на две единицы; 3) число N объектов
наблюдения длжно превышать число р
дискриминантных переменных (0<р<N-2)
не менее чем на две единицы; 4)линейная независимость м/у признаками (j), т.е. ни один из признаков не должен быть линейной комибинацией др признаков, в
противном случае он не несет новой информации; 5) нормальный закон распределения
дискриминантных переменных хij
(по признакам).
Если приведенные предположения
не удовлетворяются, то ставится вопрос о целесообразности использования дискриминантного анализа для классификации новых
наблюдений.
12.Многомерный стат анализ
задачи снижения размерности. Факторный и
компонентный анализ.
В исследовательской и
практической работе приходится сталкиваться с ситуацией, когда общее число
признаков х1, х2, х3 … хр регистрируемых на каждом из
множестве объектов (стран, регионов, семей) очень велико.
Тем не менее имеющиеся
многомерные наблюдения следует подвергать статистической выборке (осмыслить,
ввести в БВ, для того, чтобы иметь возможность использовать их в нужный
момент).
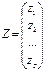 Желание статистика представить любое из наблюдений хi в виде вектора z
вспомогательных показателей.
Желание статистика представить любое из наблюдений хi в виде вектора z
вспомогательных показателей.
с существенно меньшим, чем
число р компонент р` бывает
обусловлен следующим причинам:
необходимостью наглядного
представления исходных данных, что достигается их проецированием на специально
подобранное трехмерное пространство (p`=3) или двухмерное (р`=2) или одномерное
(р`=1);
стремлением к локализму исследуемых моделей для упрощения счета и
интерпретации полученных выводов;
Ограниченными возможностями
человека в одновременном охвате большого числа частных критериев;
Например: в анализе ряда разноспекторных характеристик качества жизни человека. А
отсюда, стремление к сверстке информации и этих частных критериев и переходу к
интегральному индикатору.
Необходимостью сжатия объемов
хранимой информации (стат) в специальной БД. При этом
вспомогательные признаки z1 z2 …zр могут вбираться из
числа иходных признаков, либо явл
их линейными комбинациями.
При формировании новой системы
признаков k последним предъявляются разного рода
требования, такие как: Наибольшая информативность (в определенном смысле)
взаимная некоррелированность
Наименьшее искажение структуры
их данных; В зависимости от варианта формальной конкретизации этих требований
приходим к тому или иному алгоритму снижения размерности.
Имеется по крайней мер 3
основных тип принципиальных предпосылок, обуславливающих возможность перехода
от большего числа р- исходных показателей, состояний
исследуемой системы k существенно меньшему р` наиболее информативных переменных: дублирование
информации (наличие взаимосвязанных признаков); не информативность (малая вариательность признака при переходе от одного объекта к др); возможность агригорования
(т.е. простого суммирования или взаимного по некоторым группам).
Формально задача перехода с
наименьшими потерями от р признаков к новому набору р` м.б. описана следующим образом: Пусть Z=Z(x)=Z(Z1 Z2 … Zp`) Некоторая р` -мерная функция от исходных переменных.
И пусть Ур(Z(x)) – определенным образом заданная мера информативности р`-мерной системы признаков: Z= Z(Z1(х)
Z2(х) … Zp(х))Т
Конкретный выбор функционально
зависит от специфики реально решаемых задач и оперяется на один из возможных критериев.
Критерия автноинформативности
нацеленных на мах-ие сохранение информации,
содержащейся в исходном массиве xi , относительно
самих исходных признаков.
Критерий внешней
информативности, нацеленной на мах-ию «выжимания» из хi информации относительно некоторых внешних показателей.
Тот или иной вариант
конкретизации этой постановке приводит к конкретному методу снижения размерности,
а именно: -методу гл. компонентов; -методу факторного анализа; -метод экстремальной
группировке параметров.
Метод гл. компонент.
Во многих задачах обработки
многомерных наблюдений и в частности в задачах классификации исследователя
интересуют лишь те признаки, γ обнаруживают
наибольшую изменчивость при переходе от одного объекта к др. С др стороны не обязательно для описания состояния объекта использовать
какие-то из исходных замеренных на нем признаки (например, портной делает М изделий
но для покупки достаточно 2 значения : рост и объем груди). Следуя общей
оптимальности постановок задачи снижения размерности выражения:
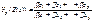 ,
,
можно принять в качестве меры
информативности p`-мерной системы показателей. Тогда
при любом фиксированном р` вектор Z искомых показателей
вспомогательных переменных (новых) определяется как линейная комбинация Z=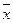 исходных
данных, где
исходных
данных, где 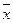 - вектор центрированных исходных данных.
- вектор центрированных исходных данных.
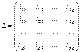 - принцип строки, γ
удовлетворяет условию ортагональностьи.
- принцип строки, γ
удовлетворяет условию ортагональностьи.
Полученных т.о. переменные и
называют гл. компонентами.
1-ой гл. компонентой явл та, γ обладает наибольшей
дисперсией. Далее компоненты располагаются по мере убывания дисперсей.
Вычисление гл. компонент. По исходным статистическим данным получить вектор ср.
значений и квалификационную матрицу ∙Σ.
Для определения коэффициентов
линейного преобразования, с помощью γ
осуществляется переход к главным компонентам необходимо решить харак-ческое уравнение.
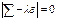
где ε
– единичная матрица соответствующего порядка, λ=(λ1,
λ2, … λр) – собств-ые
значения (числа), Σ- сигма.
найти относительные доли
суммарной дисперсии, обусловленные этим компонентом
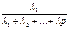 ;
; 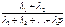 ; …
; …
К сожалению гл. компонента
бывает сложно интерпретировать.
Х1- носит самую большую
нагрузку.
Располагая исходными данными и
используя уравнение для z1 (меняя значения х) можно
посчитать значения 1-ой гл. компоненты для люб измеряемых пр-ий.
Интерпретируем z1 как
объясняющую переменную и записываем уравнения хi=f(z1)
(уравнение парной регрессии) для люб исходного показателя.
13. Измерение тесноты связи между показателями. Анализ
матрицы коэффициентов парной корреляции.
Коэф-т парной
линейной корреляции: 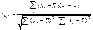 . Свойства:
1) rx,y находится в инт-ле
(-1;1); 2) rx,y>0 – связь прямая, rx,y<0 – связь обратная; 3)
. Свойства:
1) rx,y находится в инт-ле
(-1;1); 2) rx,y>0 – связь прямая, rx,y<0 – связь обратная; 3) 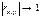 - связь
тесная,
- связь
тесная, 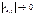 - связь
слабая.
- связь
слабая.
Пусть в исследовании
используется совокупность переменных у1, х1, х2,…, хm.
Для каждой пары можно рассчитать коэф-ты парной
линейной корреляции. В результате, получиться матрица коэф-в
парной корреляции:
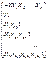 . Эта
матрица симметрична относительно главной диагонали, т.е. состоит из двух одинаковых
треугольников. Она позволяет выбрать факторы наиболее тесно связанные с
интересующей нас величиной, а также установить связь между самими факторами.
Как правило, в регрессионной модели нельзя включать факторы, тесно связанные
между собой.
. Эта
матрица симметрична относительно главной диагонали, т.е. состоит из двух одинаковых
треугольников. Она позволяет выбрать факторы наиболее тесно связанные с
интересующей нас величиной, а также установить связь между самими факторами.
Как правило, в регрессионной модели нельзя включать факторы, тесно связанные
между собой.
28.Интервальная оценка параметров моделей парной
регрессии
Для значимого ур-я регрессии строят интервальные оценки параметров a и b.
Интервальная оценка параметра a, есть:
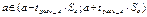
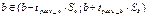
Замечание: если интервальные
границы в разные по знаку, то такие уравнения в прогнозировании использовать
нельзя, т.е. непонятно какое направление.
15.Оценка влияния факторов на зависимую переменную:
коэффициент эластичности и β-коэффициент.
Влияние факторов на зависимую
переменную оцениваются с помощью коэффициентов эластичности и β-коэффициентов.
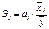
Он показывает на сколько %
увеличится результативный показатель У при увеличении соответствующего j-ого
фактора на 1%.
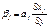 , где
, где
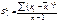 и
и 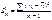
он показывает на какую
величину своего среднего квадратического отклонения
изменится результативный показатель У при увеличении соответствующего j-ого
фактора на 1-о свое среднеквадратическое отклонение.
29. Измерение тесноты связи между показателями. Мультиколлинеарность и способы ее устранения.
Пусть в исследовании
используется совокупность переменных у1, х1, х2,…, хm.
Для каждой пары можно рассчитать коэф-ты парной
линейной корреляции. В результате, получиться матрица коэф-в
парной корреляции:
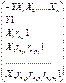 . Эта
матрица симметрична относительно главной диагонали, т.е. состоит из двух
одинаковых треугольников. Она позволяет выбрать факторы наиболее тесно
связанные с интересующей нас величиной, а также установить связь между самими факторами.
Как правило, в регрессионной модели нельзя включать факторы, тесно связанные
между собой.
. Эта
матрица симметрична относительно главной диагонали, т.е. состоит из двух
одинаковых треугольников. Она позволяет выбрать факторы наиболее тесно
связанные с интересующей нас величиной, а также установить связь между самими факторами.
Как правило, в регрессионной модели нельзя включать факторы, тесно связанные
между собой.
Одним из условий регрессионной
модели явл-ся предположение о линейной независимости
объясняющих переменных, т.е. решение задачи возможно лишь тогда, когда столбцы
и строки матрицы исходных данных линейно независимы. Для экон.
показателей это условие выполняется не всегда. Линейная или близкая к ней связь
между факторами называется мультиколлинеарностью и приводит к линейной зависимости нормальных
уравнений, что делает вычисление параметров либо невозможными, либо затрудняет
содержательную интерпретацию параметров модели. Считают явление мультик-ти в исходных данных установленным, если коэф-т парной корреляции между 2-мя переменными больше 0,8.
Чтобы избавиться от мультик-ти, в модель включают
лишь один из линейно связанных между собой факторов, причем тот, который в
большей степени связан с зависимой переменной. В качестве критерия мультик-ти может быть принято соблюдение следующих неравенств:
ryxi>rxixk, ryxk>rxixk, rxixk<0,8. если приведенные неравенства (или хотя бы
одно из них) не выполняется, то в модель включают тот фактор, который наиболее
тесно связан с у.
27.Интервальные прогнозы по линейному уравнению парной
регрессии.
В прогнозных расчетах по уравнению
регрессии определяется предсказываемое (ур) значение
как точечный прогноз ýх при хр =хк, т.е. путем подстановки в
уравнение регрессии ýх=а+bx соответствующего
значения х. Однако точечный прогноз явно не реален. Поэтому он дополняется
расчетом стандартной ошибки ýх, т.е. u и соответственно интервальной оценкой прогнозного
значения (у*)
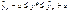
где u
рассчитывается по формуле: 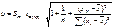 , где
, где 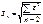 -средная квадратиче6ская ошибка, t(кр) берется из таблицы T-критерия Стьюдента с заданной
доверительной вероятностью и степенью свободы.
-средная квадратиче6ская ошибка, t(кр) берется из таблицы T-критерия Стьюдента с заданной
доверительной вероятностью и степенью свободы.
16. Обобщенный МНК.
При нарушении
гомоскедастичности рекомендуется традиционный МНК заменять обобщенным МНК.
Обобщенный МНК применяется к преобразованным данным и позволяет получать
оценки, которые обладают не только свойством несмещенности,
но и имеют меньшие выборочные дисперсии.
Предположим, что среднее
значение остаточных величин равно нулю. А вот дисперсия их не остается
неизменной для разных значений фактора, а пропорциональна величине Кi, т.е. 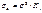 , где
, где 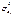 - дисперсия
ошибки при конкретном i-ом значении фактора,
- дисперсия
ошибки при конкретном i-ом значении фактора, 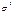 - постоянная
дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков; Кi – коэф-т пропорциональности,
меняющийся с изменением величины фактора, что и обусловливает неоднородность
дисперсии.
- постоянная
дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков; Кi – коэф-т пропорциональности,
меняющийся с изменением величины фактора, что и обусловливает неоднородность
дисперсии.
При этом предполагается, что 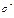 неизвестна, а в отношении величины К
выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.
неизвестна, а в отношении величины К
выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.
В общем виде для уравнения 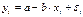 при
при 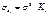 , модель
примет вид:
, модель
примет вид: 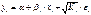 .
.
В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие
автокорреляции, можно перейти к уравнению с гомоскедастичными
остатками, поделив все переменные, зафиксированные в ходе i-ого наблюдения на 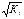 . Тогда
дисперсия остатков будет величиной постоянной, т.е.
. Тогда
дисперсия остатков будет величиной постоянной, т.е. 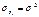 .
.
Иными словами, от регрессии у
по х мы перейдем к регрессии на новых переменных: 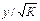 и
и 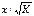 .
.
Уравнение регрессии примет
вид:  .
.
По отношению к обычной
регрессии уравнение с новыми, преобразованными переменными представляет собой
взвешенную регрессию, в которой переменные у и х
взяты с весами 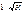 .
.
Оценка параметров нового
уравнения с преобразованными переменными приводит к взвешенному МНК, для
которого необходимо минимизировать сумму квадратов отклонений вида: 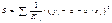 .
.
Соответственно получим
следующую систему нормальных уравнений:
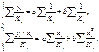 Если
преобразованные переменные х и у взять в отклонениях
от средних уровней, то коэф-т регрессии b можно определить как
Если
преобразованные переменные х и у взять в отклонениях
от средних уровней, то коэф-т регрессии b можно определить как 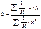 .
.
При обычном применении МНК к
уравнению линейной регрессии для переменных в отклонениях от средних уровней коэф-т регрессии b определяется
по формуле: 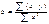 .
.
Как видим, при использовании
обобщенного МНК с целью корректировки гетероскедастичности
коэф-т регрессии b
представляет собой взвешенную величину по отношению к обычному МНК с весами
1/К.
17.Анализ эконометрических объектов и прогнозирование с
помощью модели множественной регрессии.
По полученной, адекватной и
точной моедли можно строить точечный и интервальный
прогноз.
Прогнозное значение факторных
показателей Хj можно поучить:
А) построив уравнение тренда
(если он есть)
Б) либо применить адаптивную
модель Брауна, если предпочтения надо отдать последним данным (при отсутствии
сезонности).
В) либо построив адаптивную
модель Хольтст-Уильтерса – если есть сезонность (и
курс)
Г) либо применив метод
экспериментальных оценок (и курс?)
Д) Поучив обобщенный прогноз
по всем вышеперечисленным моделям с учетом коэффициента важности.
Подставив точечный прогноз
фактора Хj в модель получим точечный прогноз
результативного показателя У. Вероятность того, что от сбудется =0, поэтому
необходимо построить доверительный интервал, в γ
с заданной доверительной вероятностью р попадет
прогнозное значение. Ширина доверительного интервала
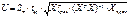 , где Sm – ср квадрат ошибка модели
, где Sm – ср квадрат ошибка модели
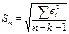 ;
; 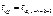 ,
,
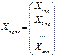
19. Системы линейных одновременных уравнений (СОУ). Взаимозависимые
и рекурсивные системы.
Регрессионное уравнение
устанавливает зависимость одной величины от совокупности факторов. Как правило,
нас может интересовать целый ряд величин у1, у2, у3…, которые зависят как от
факторов, так и между собой. Для отображения такой паутины взаимосвязей
используются системы уравнений. Они бывают 3 видов: 1. системы независимых
уравнений; 2. рекурсивные системы; 3. системы взаимозависимых уравнений.
Рекурсивные системы: 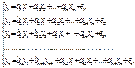
Первое уравнение в таких системах
является моделью множественной регрессии. В каждом последующем будут
содержаться как все независимые факторы, так и зависимые переменные, оцененные
ранее (предопределенные). Такие системы могут использоваться для анализа
производительности труда и фондоотдачи.
Системы взаимозависимых
уравнений: 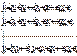 Эти системы
используют для анализа динамики цены и зарплаты.
Эти системы
используют для анализа динамики цены и зарплаты.
25.Множественная корреляция и частичная корреляция
Эк явления как правило
определяются большими числами одновременно и совокупно действующих факторов. В
связи с этим возникает задача исследования зависимости одной (или нескольких)
переменных у от совокупности переменных (х1 х2 … хm).
В таком случае для измерения тесноты связи м\у У и
факторными признаками хj (j =1 … n)
используют множественных коэффициент корреляции.
Для этого используют матрицу
парных коэффициентов корреляции м\у всеми
рассматриваемыми переменными.
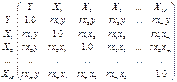
По этой матрице вычисляется
множественный коэффициент корреляции, отражающий тесноту связи м/у Y и всеми
остальными факторами.
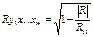 , где R –
алгебраические дополнения к соответствующим коэффициентам.
, где R –
алгебраические дополнения к соответствующим коэффициентам.
Частный коэффициент корреляции
устанавливается зависимость м\у j-ым
и k-ым фактором при исключении остальных.
21. Предпосылки МНК.
Основную информацию для
анализа качества регрессионного уравнения можно получить из ряда остатков.
Иногда только по одному графику остатков можно судить о качестве аппроксимации.
Остатки модели должны обладать опр. свойствами: несмещенность,
состоятельность, эффективность. На практике проверка этих свойств сводится к
проверке 5 предпосылок МНК: 1.случайный характер остатков (критерий поворотных
точек), 2.независимость уровней в ряде остатков (d-критерий Дарбина-Уотсона),
3.соответствие ряда остатков нормальному закону распределения(RS-критерий),
4.равенство 0 мат. ожидания остатков, 5.гомоскедастичность остатков.
1.Свойство случайности
проверяется с помощью критерия поворотных точек или критерия пиков. Уровень в
ряде остатков называется поворотной точкой, если он одновременно больше или
одновременно меньше 2-ух соседних с ним уровней. Точкам поворота приписывают
значения 1, остальным – 0. Свойство случайности выполняется, если количество
поворотных точек 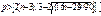 справа означает, что от выражения внутри них
нужно взять целую часть. n – количество уровней в
ряде.
справа означает, что от выражения внутри них
нужно взять целую часть. n – количество уровней в
ряде.
2.Для проверки свойства
независимости (отсутствие автокорреляции) уровней в ряде остатков используют
d-критерий Дарбина-Уотсона. В начале рассчитывают
величину d по формуле: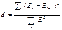 . Для этого
критерия задаются 2 таблич. границы d1 и d2.
. Для этого
критерия задаются 2 таблич. границы d1 и d2.
3.Для проверки соответствия
ряда остатков нормальному закону распределения используют RS-критерий: RS =(Emax-Emin)/SE. Emax и Emin- соотв. наибольшее и наименьшее значения уровней в
ряде остатков. SE- СКО. Если значение RS попадает в табличный интервал, то ряд
остатков распределен по норм. закону.
5.Гомоскедастичность –
постоянство дисперсии остатков по отношению к фактическим значениям фактора или
показателя. Остатки называются гомоскедастичными,
если они сосредоточены в виде горизонтальной полосы около оси xi, в противном случае остатки называют гетероскедастичными.
Для исследования гомоскедастичности применяются различные тесты. Один из них
называется тест Голдфельда-Квандта: 1) Упорядочение
значений показателя у по степени возрастания фактора х. 2) Из упорядоченной
совокупности убирают несколько «с» центральных значений: 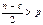 , р – число оцениваемых в модели параметров. В результате,
получается 2 совокупности данных, в одной из них значения фактора будет
наименьшими, а в другой – наибольшими. 3) Для каждой совокупности строят модель
регрессии, по которой находят остатки:
, р – число оцениваемых в модели параметров. В результате,
получается 2 совокупности данных, в одной из них значения фактора будет
наименьшими, а в другой – наибольшими. 3) Для каждой совокупности строят модель
регрессии, по которой находят остатки: 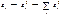 . Пусть S1
– большая сумма квадратов ошибок, а S2 – меньшая. 4) Определим отношение
. Пусть S1
– большая сумма квадратов ошибок, а S2 – меньшая. 4) Определим отношение 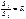 . 5) Полученное
значение R сравнивают с табличным значением F-критерия Фишера. Если Fтабл<R, то предпосылка о гомоскедастичности нарушена.
Чем больше R по отношению к Fтабл, тем более нарушена
данная предпосылка.
. 5) Полученное
значение R сравнивают с табличным значением F-критерия Фишера. Если Fтабл<R, то предпосылка о гомоскедастичности нарушена.
Чем больше R по отношению к Fтабл, тем более нарушена
данная предпосылка. 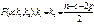 .
.
23.Модель множественной регрессии. Выбор вида модели и
оценка ее параметров
Связь между у и независимыми
факторами х1, х2, … хn можно охарактеризовать
уравнением (моделью) множественной регрессии.
Y=f (х1, х2, … хn).
Эта модель показывает, какие
значения в ср принимает результативный показатель У, если переменные Хi примут какие-то свой конкретные значения.
В зависимости от функции f будем иметь линейную или не линейную множественную
регрессию.
Тинтером было доказано, что усложнение формы связи м\у хi и у не принципиально
влияет на конечные результаты.
Линейная модель множественной
регрессии.
У=а0+а1х1+ а2х2+…+ аmхm+e
Параметры определяются с
помощью методов наименьших квадратов.
Для этого проведем все рассуждения в матричной
форме. Введем следующие матричные обозначения:
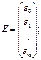
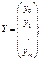

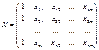 ;
; 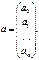
где У вектор n значений результативного показателя.
Х – матрица n значений m независимых переменных;
а матрица параметров
У=Х∙а+ε.
Заметим, что а – выборочные
оценки совокупности.
Итак, метод наименьших
квадратов требует мин-ии суммы квадратов отклонений
исходных модели значений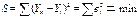 ,
, 
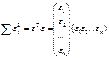
Далее: 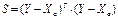
Из матричной алгебры известно,
что 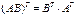 , тогда:
, тогда:
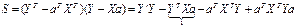
1 – это есть матрица
размерностью 1Х1, т.е. число-скаляр, а скаляр при трансформировании не меняется,
поэтому 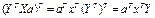 Þ
Þ 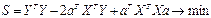
Согласно условию экстремума S
по а =0
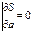 ;
; 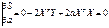
2ХТY+2aXTX=0
XTY=aXTX
Для погашения а умножим обе
части этого уравнения на (ХТХ)-1, тогда
а= (XTХ)-1∙XTY
Решение задачи нахождения
матицы, а возможно лишь в том случае, если строки и столбцы матрицы Х линейно
независимы.
22. Модель множественной регрессии. Построение системы
показателей-факторов.
Модель парной регрессии
устанавливает зависимость интересующей нас величины только от 1-го фактора. В
экономике эта ситуация абстрактная. На показатель влияет целая совокупность
факторов. Если использовать линейную математическую функцию, то в этом случае
модель множественной регрессии примет вид yi=a0+a1xi1+a2xi2+a3xi3+…+amxim+ei. Каждый из параметров модели аi
показывает, на сколько меняется исследуемая величина у при изменении соответствующего
фактора на 1 единицу. Эта модель универсальна в том смысле, что позволяет установить
зависимость показателя, как от всей совокупности факторов, так и от каждого из
них в отдельности. Эта модель применяется при изучении проблем спроса, функции
доходности акции, функции издержек производства, функции прибыли и т.д.
Построение системы
показателей-факторов. При построении системы факторов необходимо соблюдать
следующие условия: 1) должны быть количественно измеримы; 2) теоретически обоснованы;
3) линейно независимы друг от друга; 4) одна модель не должна включать в себя
совокупный фактор и факторы его образующие; 5) тесно связаны между собой. Для
реализации 5-го требования строят матрицу коэф-в
парной корреляции. На основании этой матрицы выбирают те факторы, связь которых
с величиной наиболее тесная. Затем проверяют наличие мультиколлинеарности
(МК) факторов. Два фактора МК, если 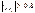 . МК
факторы нельзя включать в одну модель, нужно выбрать один из них или заменить
оба совокупной функцией
. МК
факторы нельзя включать в одну модель, нужно выбрать один из них или заменить
оба совокупной функцией
24.Проверка качества многофакторных регрессионных
моделей.
Качество модели, т.е. ее
адекватность и точность проверяется с помощью d-критерия – критерия
независимости последних уровней остаточной компоненты.
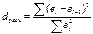
если (d`)dp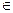 [1.36;2,0),
то остаточные компоненты не коррелированы.
[1.36;2,0),
то остаточные компоненты не коррелированы.
если (d`)dp>2, то переходим к d`=4 - dp
если (d`)dp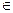 [1.08;1,36),
то используют
[1.08;1,36),
то используют
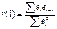 ;
; 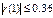 Þ ………………………………..
Þ ………………………………..
Далее критические повороты
точек (о случайности значений остаточной компоненты)
При использовании поворотных
точек следует обратить особое внимание на сущ-ие
аномальных значение εi .
Если какие-то значения εi .явл аномальными, то
соответствующие I-ое наблюдение из данных надо
убрать.
Далее R/S-критерий
///соответствие распределения остаточной компоненты по нормальному закону///.
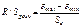 , если R/Sрасч принадлежит соответствующему интервалу (критические
значения R/S стр 72 методички эконометрика), то остаточная
компонента распределена по нормальному закону. При выполнении всех критериев
модель адекватна.
, если R/Sрасч принадлежит соответствующему интервалу (критические
значения R/S стр 72 методички эконометрика), то остаточная
компонента распределена по нормальному закону. При выполнении всех критериев
модель адекватна.
Точность модели можно оценить
с помощью средней относительной ошибки.
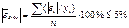 Þ модель точна и ее можно использовать в прогнозировании.
Þ модель точна и ее можно использовать в прогнозировании.
Влияние факторов на зависимую
переменную оцениваются с помощью коэффициентов эластичности и β-коэффициентов.
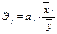
Он показывает на сколько %
увеличится результативный показатель У при увеличении соответствующего j-ого
фактора на 1%.
 , где
, где
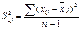 и
и 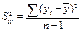
он показывает на какую
величину своего среднего квадратического отклонения
изменится результативный показатель У при увеличении соответствующего j-ого
фактора на 1-о свое среднеквадратическое отклонение.
26.Нелинейная регрессия. Нелинейная модель и их
линеаризация.
Различают 2 класса нелинейных
регрессий:
-регрессии нелинейные
относительно включенных в анализ объясняющих переменных, но линейные по
оцениваемым параметрам;
-регрессии, нелинейные по
включенным параметрам.
Примером нелинейной регрессии
по включаемым в нее объясняющим переменным могут слуюить
следующие функции:
Полиномы разных степеней:
y=a+bx+cx2+ε,
y=a+bx+cx2+dx3+ ε;
Равносторонняя гипербола: 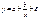
К нелинейным регрессиям по
оцениваемым параметрам относятся функции:
Степенная y=axb
ε
Показательная y=abx ε
Экспоненциальная у=уa+bx ε
Линеаризация нелинейной модели
представляет собой преобразование используемой модели в линейную путем замены
переменных на нестепенные.
Так, в параболе второй
степени у=а0+а1х+а2х2+ ε заменяя
переменные х=х1, х2=х2, получим двухфакторное уравнение линейной регрессии:
у=а0+а1х1+а2х2+ ε, для оценки параметров Ã используется МНК.
Соответственно для полинома
третьего порядка y=a+bx+cx2+dx3+ ε при замене х=х,
х2=х2, х3=х3,, получим трехфакторную модель линейной регрессии: у=а0+а1х1+а2х2+
а3х3 + ε
|
Название ф-ии
|
Вид модели
|
Заменяемые переменные
|
Вид линеаризированной
модели
|
|
Показательная
|
Ln y = Ln a+ х ln
b
|
Ln y = Y, Ln a = α, Ln b =β
|
Y = a + xbα+x β (Þ a=eα, b=eβ)
|
|
Степенная
|
Ln y = Ln a+ b ln x
|
Ln y = Y, Ln a = α, Ln x =x
|
Y = a
+ bxα+bx
|
|
гиперболическая
|
Y = a
+ b/x
|
1/x=X
|
Y = a
+b X
|
1.Классификация эконометрических моделей
Эконометрические модели
делятся на линейные и нелинейные.
Линейная модель парной регрессии
имеет вид: у=bх+a+e
b - коэф-т
регрессии, показывающий, как изменится у при изменении х
на единицу
a - это свободный член,
расчетная величина, содержания нет.
e - это остаточная
компонента, т.е. случайная величина, независимая, нормально распределенная, мат
ожид = 0 и постоянной дисперсией.Присутствие
e в модели свидетельствует
о том, что функциональной зависимости м\у у и х нет. На изменение у оказывает влияние не только фактор х, но и какие-то др не учтенные
моделью факторы.
Первой задачей регрессионного
анализа явл получение значения параметров a и b. Найти эти параметры мы не можем (пришлось бы обследовать ген
совокупность), поэтому находим выборочные оценки этих параметров.
ŷ = a + b
x
Для нахождения выборочных
оценок используем метод НК
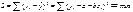
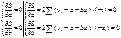
решением системы нормальных
уравнений будет:
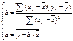
выборочные оценки для ур-я (1)
очевидно, что мин регрессия
будет иметь место только в том случае, если 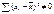 . если хi совпадает с
. если хi совпадает с 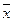 в этом случае зависимость отсутствует.
в этом случае зависимость отсутствует.
Нелинейная модель. уравнение
зависимости между Уи Х может быть представлено
степенной функцией У от Х,  , показательной
, показательной
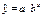 ,
гиперболической
,
гиперболической 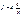 и д.р.
и д.р.
Для оценки параметров в этих
случаях метод наименьших квадратов можно применять после логарифмирования, либо
после введения новой переменной.
Для показательной функции:
ln y=ln a+x
ln b
Y α β
Y = α
+ х β Þ а = еα; b=еβ
для степенной функции
ln y=ln a+b
ln x
Y α X
Y = α
+ β
Для гиперболической функции
у=а+b/x
1/х=Х
У=а+bХ