2

Оглавление

Введение 3

1. Значение страховых тарифов для обеспечения

финансовой устойчивости страховщика 4

2. Состав и структура тарифной ставки 6

3. Особенности построения тарифных ставок по страхованию жизни 11

4. Построение тарифных ставок по рисковым видам страхования 16

Задача 25

Заключение 26

Список литературы 27

Приложение 28

ВВЕДЕНИЕ

Рыночные преобразования в экономике России вызвали коренное изменение роли и места страхования в системе мер, обеспечивающих безопасность хозяйствующих субъектов, населения и российского государства в целом. Развитие отечественного страхового рынка стало одной из важных задач экономического реформирования страны. Ее решение способно во многом обеспечить непрерывность общественного воспроизводства.

Система воздействия на страховой рынок со стороны государства в России до сих пор окончательно не сформировалась. Неустойчивость этой системы вызвана не только внутренними факторами его развития, но и является прямым следствием макроэкономических процессов, наблюдаемых в реформирующейся экономике страны.

Важно подчеркнуть особый характер внешней сферы развития российского рынка страховых услуг. В условиях переходного периода добровольное страхование носит фрагментарный характер. Общественная потребность в этом виде услуг значительна, но организационно она лишь начинает формироваться. Очевидно в этом одна из причин односторонности, а, следовательно, и шаткости государственной политики в области страхования, что, в свою очередь объясняет низкую степень развитости страхования финансовых рисков. Незащищенность юридических и физических лиц влечет за собой существенные бюджетные затраты по ликвидации последствий стихийных бедствий, оказанию социальной поддержки гражданам. Незрелость российского страхового рынка - один из факторов слабости инвестиционного климата и общих условий экономической деятельности.

Преодоление неразвитости сферы страхования вообще и финансовых рисков в частности превращается в России в проблему общегосударственную. Между тем, рынок страховых услуг может выступать в качестве важного стабилизирующего фактора экономики.

1. Значение страховых тарифов для обеспечения финансовой устойчивости страховщика

Страхование в развитой рыночной экономике выполняет роль экономического стабилизатора, механизма защиты от случайных потерь. Страхование может применяться для организации страховой защиты различных отраслей народного хозяйства, финансового обеспечения непрерывности производственного процесса в условиях различных чрезвычайных событий, а также для сохранения уровня благосостояния граждан. Кроме того, страхование включено в сферу финансово-кредитных отношений, и, следовательно, обладает способностью само оказывать регулирующее воздействие на воспроизводственный процесс.

Более чем что-либо другое, жизнеспособность механизма страхования зависит от способности страховщика выполнять договорные обязательства при предъявлении претензий по полису при наступлении страхового случая. Поэтому большая роль отводится оценке финансового состояния страховщика.

Выравнивание и разделение рисков (раскладка ущерба), при формировании рационального страхового портфеля страховой организацией, реализуется с помощью страхового тарифа. Вопрос оптимизации тарифной политики страховщика является весьма актуальным с точки зрения обеспечения его финансовой устойчивости.

Страховой тариф представляет собой взнос страхователя с единицы страховой суммы, и может быть выражен в рублях со страховой суммы или в процентах от нее [5; 7]. Тариф определяется страховщиком, (исключение составляют тарифы по обязательным видам страхования, определяемые законодательными актами) на основе ожидаемой совокупности объектов страхования и используется для определения страхового взноса как цены страховой защиты.

Экономическое содержание страхового тарифа можно определить как единицу измерения взаимных обязательств страховщика и страхователя, принимаемых ими при заключении страхового договора, или, иначе говоря, как выражение того обязательства, которое страховщик принял на себя по отношению к страхователю в пределах и на условиях, определяемых страховым договором.

Учитывая сложность оценки страховых рисков и расчета страховых тарифов для начинающих страховую деятельность, при недостаточности статистики у страховых организаций, Федеральная служба России по надзору за страховой деятельностью рекомендует использовать предлагаемые методики расчета страховых тарифов по рисковым видам страхования. («Методики расчета тарифных ставок по рисковым видам страхования», утвержденные Федеральной службой Российской Федерации по надзору за страховой деятельностью от 8 июля 1993г. №02-03-36) [5].

Рекомендуемые методики расчета тарифных ставок нашли признание со стороны страховых организаций, большинство компаний используют именно рекомендованные методики расчета. Но существуют также критические замечания, так как некоторые параметры расчета неадекватны сложившейся ситуации на рынке страховых услуг.

2. Состав и структура тарифной ставки

Определение тарифной ставки можно понять после того, как будут понятны схема работы страхового рынка. Так страховщик и страхователь заключают между собой сделку на то, что страховая компания, окажет определенную услугу своему клиенту при наступлении страхового случая, указанного в договоре. Любая услуга имеет свою стоимость или цену, которая выражается в страховом взносе (тарифе, премии), которую страхователь уплачивает страховщику. Страховая премия устанавливается при подписании договора и остается неизменной в течении срока его действия.

Реальная стоимость страховой услуги состоит в том, что если наступил страховой случай, то страховщик, например, оплачивает затраты страхователя, возмещая ему тем самым ущерб, понесенный им в связи с происшедшим. Необходимо определить, как страховщик определяет для себя данную цену, чем он руководствуется в процессе ее установления.

Во-первых, величина премии должна быть достаточна, чтобы:

- ответить по договору страхования в размере предлагаемых претензий;

- создать страховые резервы;

- покрыть издержки страховой компании;

- обеспечить определенный размер прибыли.

Во-вторых, цена страховой услуги, как и всякая рыночная цена, колеблется под влиянием спроса и предложения. Она варьируется в определенном интервале, нижняя граница которого определяется равенством между поступлениями платежей от страхователей и выплатами страхового возмещения (страховых сумм) по договорам плюс издержки страховой компании (П_н=А+З). Понятно, что при таком уровне цены, страховщик не получи ни какой прибыли. Верхняя граница цены страховой услуги определяется размером спроса на нее и величиной банковского процента (П_в=F(D_s_;i). Тогда П_н<=П_X_.<=П_в.Влияние спроса подтверждается тем, что стоимость данной страховой услуги определяется потребностью в ней. Если спрос высокий, то растут цены на страховые услуги, вследствие этого появляется множество страховых фирм конкурентов, после чего страховые тарифы приходят к определенному уровню (выравниваются) [1; 2].

Динамика банковского процента в сравнении со страховыми тарифами определяют решения клиента по поводу того, как ему противостоять своим рискам. То есть, он определяет, что для него лучше: взять ссуду в банке или обратиться к страховой компании. Кроме этого, средства клиентов, аккумулированные в страховой компании, инвестируются в различные виды деятельности, в том числе кладутся на депозит в коммерческие банки, предоставляются в виде кредитов, вкладываются в недвижимость и ценные бумаги и т.д. В данном случае страховая компания может конкурировать с банком, в процессе чего она соизмеряет свои страховые тарифы со ставками в коммерческом банке, стараясь повлиять на выбор клиента. Другой вариант - доходы от инвестиционной деятельности покрывают расходы страховой компании и идут на формирование прибыли, тем самым, позволяя страховщикам снижать цены страховых услуг.

Цена страховой услуги определяется также некоторыми специфическими факторами, такими как: состояние дел страховой компании, величина и структура ее страхового портфеля, управленческие расходы, доходы, которые страховщик получает от инвестиций временно свободных средств и т.д. [11].

Страховая услуга хотя и специфический, но все же товар, а, следовательно, она имеет определенный жизненный цикл, который, в свою очередь, влияет на величину стоимости страховой услуги. Жизненный цикл страховой услуги имеет вид параболы, который определяет тенденцию изменения размера страхового тарифа во времени.

Цена страховой услуги на языке страхования называется страховой премией, и имеет определенную структуру, элементы которой должны обеспечивать финансирование страховщика. Структура страховой премии представлена в Таблице 1.

Таблица 1

Структура страховой премии

Элемент премии	Назначение
Нетто премия по риску + Страховая надбавка Е₁(X)+Н(х)	Покрытие ущерба при наступлении страхового случая и формирование страховых резервов
+Надбавка на покрытие расходов З(X)	Оплата расходов страховщика.
+Надбавка на прибыль V	Формирование прибыли
Итого: Брутто-премия (страховой тариф) П(X)	Все вышеперечисленное.

Нетто-премия – самая необходимая и неопределенная часть страхового тарифа. Она необходима для того, чтобы вовремя и сполна рассчитаться с клиентом, то есть возместить его потери после наступления страхового случая. Однако, в момент калькуляции цены величина ущерба неопределенна. На основе данных об ущербах за прошлый период рассчитывается частота наступления страховых случаев, к ним приведших, и их вероятность(q), после чего определяется средняя величина ущерба и их распределение. Другими словами, согласно договору страхования страхователь уплачивает страховщику определенную сумму (страховую премию), после чего он имеет право получить страховую сумму S после наступления страхового события. Так как вероятность страхового случая определена, то размер страховой премии определяется как: П=S*q (принцип финансовой эквивалентности). Нетто-премия – аванс за оказание услуги, по возмещению ущерба, минимальная оплата за риск, с ним связанный [1; 4].

Техника расчета страховых тарифов совершенна с математической точки зрения, однако, она не подтверждается при ее практическом применении. Даже при очень хорошей информации об ущербах, реальные ущербы превосходят его реальную величину в 50% случаев. Для того чтобы гарантировать клиентам страховую защиту, страховым организациям приходится перестраховываться, и к собственно нетто-премиям по риску добавлять страховую надбавку. Она необходима, чтобы финансировать случайные отклонения реального ущерба над ожидаемыми показателями. Кроме того, она страхует ущербы, связанные с информационными ошибками.

Остальные составляющие тарифной ставки относятся к экономике страхового предприятия, их определение – это задача экономистов и бухгалтеров. Их расчеты схожи с подобными расчетами в других организациях и не имеют особых отличий. Другое дело обстоит с расчетом нетто-премии, исчисление которой можно отнести к страховой математике. Для страховщика данная задача является самой важной, самой сложной и самой ответственной. Главная проблема состоит в неопределенности ущерба на момент калькуляции тарифа. Определение-нетто ставки неразрывно связано со всей деятельностью страховой компании, она влияет на затраты, на прибыль и на уровень ее развития.

Расчет нетто-премии состоит в установлении закономерности для калькулируемого риска. В общем случае это вероятностное распределение общего ущерба от риска на калькулируемый период. Кроме того, устанавливаются некоторые параметры, характеризующие данное распределение, такие как средняя величина, рассеяние и т.д.

S1,S2,…,Sn. – страховые суммы.

q1,q2,…,qn – вероятности ущербов.

P1,P2,…,Pn – премии от страхователей.

X1,X2,…,Xn – ущербы.

P1,p2,…, pn - вероятность того, что страховое событие не наступит, и не приведет к затратам на покрытие ущерба.

Для определения вероятностей ущербов необходима статистическая информация за предыдущие периоды по подобным страховым случаям. Чем больше анализируемый период, то есть чем длиннее история страховых событий, а, следовательно, чем больше совокупность исследуемых данных, тем точнее определяются вероятности и устанавливаются закономерности рисков.

Также важно определить факторы риска, такие как число ущербов и затраты на их ликвидацию. Если определены наиболее важные факторы, дающие объяснение закономерности риска, то они представляют собой тарифные факторы. Однородные факторы объединяются в группу тарифных факторов. В общем, при формировании исходной базы для тарифных расчетов используются три вида информации: данные индивидуальных ущербов по единичным рискам, ущербы по тарифным группам, и данные по всей рисковой совокупности.

В теории риска существуют отлаженные методы расчета страховой премии, которые полагаются на методы теории вероятностей и статистики. Итак, страховая премия, представляющая собой сумму нетто-премии и страховой надбавки, выражается следующей формулой: П(X)=Е₁(X)+Н(X).

Страховая сумма зависит от величины ущерба, поэтому S=f(x). Нетто-премия зависит как от ущерба, так и от величины страховой суммы (Е=f1(s)=f2(x)=Е(Х)=Е(S)). Данные зависимости определяются вероятностями наступления страховых событий, а, следовательно, нужно знать и понимать характеристики случайных величин. Нетто-премия является случайной величиной, хотя и зависит от вполне определенной суммы страховой суммы. Для ее расчета, необходимо использовать формулы и применять закономерности из теории вероятностей [1].

3. Особенности построения тарифных ставок по страхованию жизни

Страхование жизни обуславливает ряд особенностей, которые влияют на выбор форм и методов анализа подготовки и проведения страховых операций. Можно выделить основные факторы, которые влияют на методику расчета тарифных ставок по страхованию жизни:

1. Объектом договора по данному виду страхования является жизнь, здоровье и трудоспособность граждан. Количественные показатели, характеризующие продолжительность жизни и смертность среди населения страны централизовано собираются и обрабатываются в федеральных и региональных органах статистики. На основании подобных данных составляются таблицы смертности, которые используются страховщиками при расчете нетто-ставок по страхованию жизни.

2. Договоры страхования жизни, обычно, заключаются на длительный срок. Период времени между уплатой взносов и моментом выплат достигает нескольких лет. В течение этого срока за счет инфляции и прибыли, получаемой от инвестирования временно свободных средств, стоимость страховых взносов изменяется. Чтобы учесть подобные изменения применяются методы финансовых исчислений (дисконтирование) [3; 6; 11].

В страховании жизни неопределенность связана со случайным характером продолжительности человеческой жизни. Поэтому страховщики должны располагать данными для расчета вероятностей дожития до определенного возраста лиц различного пола. Источником таких данных являются таблицы смертности (Приложение 1), составляемые на основе переписи населения.

Таблица смертности – числовая модель процесса вымирания по возрастам некоторой абстрактной совокупности людей [10].

Прежде чем начать непосредственное описание методов расчета страховых аннуитетов и нетто-тарифов, необходимо сформулировать общие принципы определения нетто-премий в личном страховании.

В страховании жизни, как и в любом из видов страхования должно соблюдаться условие превышения страховых премий над страховыми выплатами (Е(Р)+I>=E(S)), где I – доход от инвестиций временно свободных средств. Величина страховых выплат является случайной величиной, и нельзя заранее предсказать точную сумму страховых выплат. За счет большого числа застрахованных, статистические данные однородны и обладают должной степенью надежности. Поэтому, вероятность отклонения реальных величин от их математического ожидания ничтожно мала. Вследствие этого, в актуарных расчетах принято использовать вероятную (ожидаемую) стоимость выплат. Тоже происходит и суммами нетто-премий. Их величина зависит от случайной величины S, а, следовательно, является величиной случайной.

К моменту осуществления выплат страховщик должен обладать фондом, равным вероятной стоимости выплат. Он определяет для себя будущую стоимость выплат и размер требуемого страхового фонда. Так как страховщик инвестирует свободные средства, то они ему приносят доход, который изменяется в зависимости от нормы доходности r, темпа инфляции (h), и ставки налогов (g). Тогда дисконтирование происходит по скорректированной ставке i=r(1-g)+h/100. Страховая премия выплачивается в момент заключения договора, то есть в современный момент времени, а страховые выплаты спустя определенное время. Поэтому, для их сравнения необходимо дисконтировать страховые выплаты, приводя их стоимость к сегодняшнему дню.

В страховании жизни нетто-премии иногда уплачиваются не одной суммой, а серией платежей, в различные периоды времени (в рассрочку). Для их учета страховщику приходится как нетто-премии, так и страховые выплаты приводить к одному моменту времени, иначе, при незапланированном прекращении договора, страховщик недополучит часть причитающихся ему премий [11].

Вышесказанное можно представить в виде неравенств, которые показывают основные принципы расчета тарифных ставок:

1. E+I>S – Нетто-премия с учетом дохода, от инвестиций должна превышать страховую выплату. Если данное равенство не будет соблюдаться, то страховщик обанкротится.

2. E+I>S_p – Сумма выплат – величина случайная, так как неизвестно по каким договорам приходится возмещать ущерб. Поэтому в актуарных расчетах применяют ее наиболее вероятное значение (S_p).

3. E>S_p-I – Современная вероятная стоимость выплат (разница между суммой выплат и накопленных доходов) не должна превышать стоимость единовременной нетто-премии.

4. E_p-I_E>S_p-I – Сравнение вероятной стоимости выплат происходит не с реальными суммами нетто-премий, а с их наиболее вероятным значением (математическим ожиданием). Современная вероятная стоимость нетто-премий, уплаченных в рассрочку, должна быть меньше, чем современная стоимость выплат [10].

Получается, что нетто-премии – доходы страховой компании, а страховые выплаты – ее расходы, причем и те и другие носят случайный характер. Так как в страховании жизни затронуты значительные периоды времени, в рамках которых изменяется стоимость денег пропорционально ставке i, то расчетные данные необходимо приводить к одному моменту времени.

Принцип финансовой эквивалентности (P=Sq) в страховании жизни несколько видоизменен. Пусть P – размер премии, q_n – вероятность страхового события (смерть застрахованного через n лет после начала страхования). Если страховое событие произойдет на первом году страхования, то страховщик получит сумму Р, если на втором году – 2Р, и т.д. Математическое ожидание такого ряда премий составит: Pq₁+2Pq₂+3Pq₃+…+nPq_n. Однако, премия выплачивается в разные моменты времени. С учетом этого фактора данную величину необходимо привести к одному моменту времени (к начальному): E(P)=P(q₁+(1+v)q₂+(1+v+v²)q₃+…+(1+v+…+vⁿ^-1)q_n), где v=(1+i)^-1-дисконтный множитель. Е(Р) – дисконтированное математическое ожидание страховых премий.

Теперь рассмотрим совокупность страховых выплат. Допустим, они выплачиваются в конце года, в котором имел место страховой случай. Тогда математическое ожидание выплаты в первом году составит Sq₁, во втором году -Sq2, и т.д. С учетом фактора времени математическое ожидание страховых выплат выглядит так: E(S)=S(vq₁+v²q₂+…+vⁿq_n).

Как известно, E(S)=E(Р). Подставляя известные значения в данное равенство можно определить размер нетто-премии.

Зная основные принципы формирования нетто-премии в страховании жизни можно перейти к рассмотрению методов ее расчета. Итак, основной показатель таблицы смертности – число людей l_x в возрасте х лет, оставшихся в живых из первоначальной совокупности l₀ (обычно равной 100000 человек). Величины l_x (кроме l₀) определяют расчетным путем на основе заданных вероятностей смерти (q_x)в возрасте х лет, или на основе количества умерших (d_x). Указанные вероятности получают на основе данных статистики населения с последующим усреднением и сглаживанием.

Показатели таблицы смертности связаны следующими соотношениями:

- l_x₊₁=l_x-d_x;

- d_x=l_x*q_x;

- q_x=1-p_x=1-l_x+1/l_x=d_x/l_x .

Для определения страховых тарифов необходимо знать страховые вероятности в страховании жизни и действия над ними:

1. _np_x=l_x₊_n/l_x– вероятность прожить n лет лицо, дожившим до возраста х лет.

2. p_x=1-q_x=1-d_x/l_x=l_x₊₁/l_x– вероятность человеком, дожившим до х лет, прожить еще 1год.

3. _nq_x=1-_np_x=(l_x-l_x₊_n)/l_x – вероятность умереть в интервале возрастов от x лет до n лет.

4. _mq_x=_mp_x*q_x₊_m=(l_x₊_m/l_x₎*(d_x₊_m/l_x₊_m₎=d_x₊_m/l_x - вероятность дожить до возраста х лет и умереть в возрасте x+m лет в течении 1 года.

5. _m_/_nq_x=_mp_x*_nq_x₊_m=(l_x₊_m/l_x₎*(l_x₊_m-l_x₊_m₊_n)/l_x₊_m=(l_x₊_m-l_x₊_m₊_n)/ l_x– вероятность дожить до x+m лет и умереть в возрасте от x+m лет до x+m+n лет [4].

4. Построение тарифных ставок по рисковым видам страхования

В каждой страховой компании со временем накапливается опыт вместе с которым формируется тарификационная система. Другими словами, каждый страховщик составляет схемы рисков, наподобие таблиц смертности, откуда можно определить вероятность наступления страхового случая, по тем видам страхования, которыми занимается страховая компания.

Тарификационная система представляет собой некую взаимосвязь данных по рисковым видам страхования. Она выглядит следующим образом. Все страхуемые объекты делятся на несколько крупных категорий, для каждой из которых рассчитывается базовая тарифная ставка. Кроме того, страховщик описывает факторы риска, которые он учитывает при составлении договора страхования. Каждый фактор риска входит в расчет тарифной ставки в виде поправочного коэффициента.

При заключении договора страхования, прежде всего, определяется принадлежность страхуемого объекта к тарификационной группе, на основании чего определяется базовая тарифная ставка. Потом анализируются факторы риска, присущие данному договору страхования, и определяются поправочные коэффициенты [8].

Создание тарифных ставок по каждой категории страхуемых объектов, т.е. процесс тарификации, обеспечивает создание страхового фонда, необходимого для выполнения обязательств страховщика, с минимальной долей отклонения от требуемого размера фонда. Например, если использовать одну среднюю тарифную ставку, для формирования страхового фонда, то его размер может сильно отличаться от истинных значений величин ущербов.

Пусть страховые события первой группы наступают с вероятностью q1, страховые события второй группы – с вероятностью q2, а страховые события группы N – с вероятностью qn. Тогда средняя вероятность по данному виду страхования 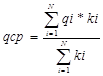, где ki – число застрахованных по каждой группе. Чем неоднороднее страховые события в группах, чем больше число групп страховых событий, тем сильнее qср отличается от qi.

Пусть страховой фонд B1, созданный на основании нетто-премий, которые, в свою очередь, рассчитываются с применением qср, а B2 – с применением qi. Тогда В1 будет тем сильнее отличаться от истинного В2, чем больше разница между qср и qi. Хорошо если после применения нетто-ставок В1>B2, тогда страховщик сможет ответить по обязательствам страхователей, а, если наоборот, то страховая компания понесет убытки.

Если рассматривать тарификационную систему с коммерческой точки зрения, то необходимо проанализировать поведение страхователя при выборе страховой услуги, предлагаемой определенным количеством компаний. Пусть эти компании разработали одинаковые страховые продукты. При этом первая половина компаний использует тарифы рассчитанные на основе qi, другая – на основе qср. Существует N групп страховых событий, страхование каждого из них пользуется определенным спросом, который зависит от цен на данный вид страхования (от нетто-премии). Чем больше цена, тем ниже спрос, и наоборот. Если нетто-премия первой группы страховщиков больше чем у второй группы по i-тому виду страхования, то в конкурентной борьбе выигрывает компания, со страховыми тарифами рассчитанными на основании qср, и наоборот. Все равно, лучше индивидуально рассматривать каждое страховое событие и применять вероятности qi – отдельные для каждого события. Это хотя и затрудняет расчеты, однако позволяет быть уверенным страховщику в своей платежеспособности [8; 9].

Факторы риска – это различные составляющие, влияющие на наступление страхового события. Например, если страховой случай – авария, то факторы риска – водительский стаж, стоимость автомобиля, физическое состояние водителя, время года и т.д.

Расчет тарифных ставок необходим для расчета страхового фонда, такого, чтобы ответить по всем договорам страхования, то есть выплатить все причитающиеся страховые суммы. Размер страхового фонда определяется размером страхового тарифа, который нужно определить.

Для нахождения нетто-премии необходимо сначала определить размер страхового фонда. Основное и очевидное условие платежеспособности страховщика - размер фонда должен превышать размер страховых выплат. Зная это, страховая компания заранее задает для себя вероятность того, что величина страхового фонда (В) превысит размер страховых выплат(S), то есть: P(S<B)>=y. Где y – заданная гарантия безопасности. Если число договоров N, а Vi – выплата по каждому договору страхования, то 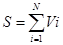- сумма убытков страховщика.

Страховой компании заранее неизвестно наступит ли событие Vi, так же ему не известен размер наступившего ущерба Vi, который может колебаться в интервале от Vmin до Vmax. Отсюда следует, что Vi – величина случайная, определяемая двумя вероятностями. Как известно из теории вероятностей, сумма случайных величин есть величина случайная. Поэтому S – случайная величина, которая может быть задана законом распределения с помощью функции распределения F(x).

Если x – действительное число, Х – случайная величина, а F(x) – вероятность того, что X<x, тогда F(x)=P(X<x). Пусть S=x, а В – страховой фонд (сумма нетто премий), тогда F(B)=P(S<B)>=y, или F(B)>=y. То есть, функция распределения случайной величины должна принимать значения большие или равные y. В свою очередь плотность распределения определяется следующим образом: f(x)=F’(x) => f(B)=F’(B).

Для того, чтобы определить размер фонда, который бы с вероятностью y обеспечивал финансовую устойчивость страховщика, необходимо найти такую величину В, при которой функция распределения F(B) случайной величины S будет больше или равна y. Для этого необходимо:

1. Найти закон распределения случайной величины S.

2. Решить приведенное выше неравенство, относительно В.

3. Вычислить отдельную нетто-премию (страховой тариф) [9].

Допустим:

1. Что наступление одного события не зависит от наступления другого, тогда все события ведущие к страховым выплатам (убыткам) – события независимые.

2. Что в массовых рисковых видах страхования ущербы по рискам не сильно отличаются друг от друга, поэтому можно предположить, что рассеяние выплат по ущербам не будет велико, а, следовательно, наиболее вероятные размеры выплат не будут сильно отличаться друг от друга. Тогда, числовые характеристики ущербов (Vi) будут одинаковы:

- Математическое ожидание выплат: mv = mv1=mv2=…=mvN.

- Среднее квадратическое отклонение выплат: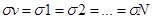

Случайная величина S представляет собой сумму очень большого числа других случайных величин (Vi), влияние каждой из которой не оказывает сильного влияния на S. Тогда согласно центральной предельной теореме (Ляпунова) величина S распределена по нормальному закону:

1. Математическое ожидание случайной величины S: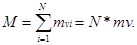

2. Cреднее квадратическое отклонение случайной величины S: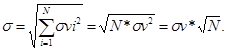

3. По определению, нормальное распределение описывается плотностью: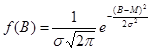

4. Так как дифференцирование – действие обратное интегрированию, то функция распределения задается формулой: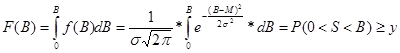

5. Для того, чтобы можно было решить приведенное выше неравенство, необходимо привести функцию распределения S к другому виду, что позволит пользоваться табличными значениями. Для этого введем новую переменную z.

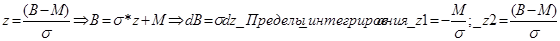
Тогда,

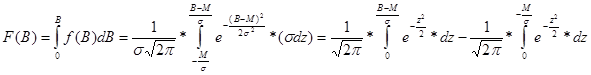
7. Табличная функция Лапласа: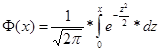

8. В итоге получим: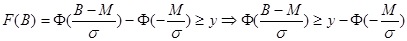

9. Можно предположить, что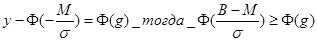

10. По определению функция распределения является неубывающей, поэтому: 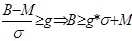, значение g определяется из таблицы значений Ф(g). Однако, предварительно необходимо найти Ф(-M/s), задать y, и определить M b s.

11. Убыток страховщика по i-тому договору представляет собой случайную величину Vi, которая распределена следующим образом:

- Если страховой случай не наступил (вероятность такого события равна 1-q), тогда выплата по договору i равна 0.

- Если страховой случай наступил (вероятность такого события равна q), то выплата по данному договору может принять любое значение из интервала (0,Vi), в зависимости от тяжести ущерба. Для массовых рисковых видов страхования наступление мелких ущербов чаще, чем наступление крупных, то есть величина ущерба Vi описывается плотностью вероятности f(Vi)=k*e^-^kVi(показательное распределение), где k- постоянная положительная величина, задающая определенный уровень ущербов. Если величина ущербов распределена по данному закону, математические характеристики ущербов определяются так:

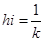- - математическое ожидание величины ущерба.

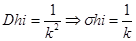- - дисперсия и среднее квдратическое отклонение, соответственно.

12. Ущерб Vi характеризуется двумя вероятностями, следовательно, он задается двумя законами распределения. Каждая величина ущерба имеет свое математическое ожидание (наиболее вероятное значение) и среднее квадратическое отклонение, которые у всех ущербов одинаковые, так как застрахованные объекты достаточно однородны. Кроме этого наступление страхового случая – величина также случайная. Поэтому математическое ожидание того, что случай ущерба Vi не наступит определяется так: mv=q*hi, где hi-математическое ожидание величины ущерба Vi. А среднее квадратическое отклонение:

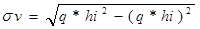
13. Для общей суммы ущерба математические характеристики вычисляются по формулам:

- .

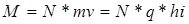
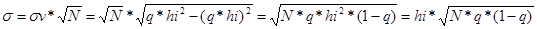14. Размер страхового фонда определяется неравенством - 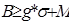. Подставим сюда известные значения: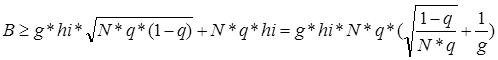

15. Зная минимальный размер страхового фонда можно определить минимальную нетто-премию или страховой тариф. Логика данного заявления следующая;

- Страховой фонд состоит из страховых премий по всем N договорам =>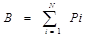

- Страховая премия определяется как произведение страхового тарифа на страховую сумму по данному договору: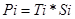

- Страховой тариф одинаков по всем договорам, поэтому: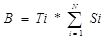

- Вместо отдельных страховых сумм по каждому договору удобнее использовать среднее ее значение, что позволяет однородность рисковых событий, тогда: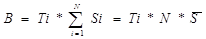

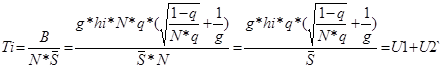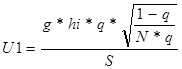- Откуда: , где , а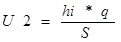

- Условно можно предположить, что U1 –основная часть нетто-ставки, а U2 – рисковая надбавка.

Расчет тарифных ставок производится по группам страхуемых объектов в соответствии с разработанной тарифной системой. В результате данного расчета страховщик должен получить для каждой группы базовую тарифную ставку (брутто). Выше была выведена формула расчета брутто-ставки: 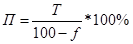, где Т – нетто-ставка, f – доля нагрузки в брутто ставке. Доля нагрузки принимается одинаковой для всех тарификационных групп в рамках одного страхового продукта.

Для определения нетто-ставки страховщик должен определить гарантию безопасности (y), вероятность наступления страхового случая (q), математическое ожидание величины страховой суммы (М), математическое ожидание величины выплаты по одному страховому случаю hi. Указанные величины являются параметрами теоретического распределения убытков. Они определяются из статистических данных [8; 10].

Пусть необходимо определить размер тарифной ставки по данным страховой компании, накопленным за год, по массовому виду страхования. Для этого выбирается некоторая совокупность договоров страхования. При этом все застрахованные объекты должны быть однородны, число договоров как можно больше, все договоры заключены на один и тот же срок и к моменту расчета полностью истек срок их действия.

1. Итак, имеется N договоров, а S1,…,Si,…,SN – причитающиеся страховые выплаты по ним.

2. V1,…,Vi,…,VW – W наступивших страховых событий, а, следовательно реально уплаченные страхователям суммы из числа SN.

3. Тогда вероятность наступления страхового случая определяется частотой его наступления: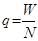 Это требование выполняется тогда, когда по договору страхования предусмотрена выплата не больше 1 страховой суммы, то есть частота должна быть меньше единицы.

4. Из теории вероятностей известно, что математическое ожидание приближеноо равно среденй величине, поэтому:

- Математическое ожидание одной выплаты: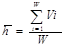

- Математическое ожидание суммы выплат: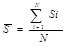

5. Страховщик определяет для себя гарантию безопасности y.

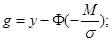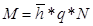6. Определяется переменная g: где , а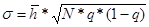

7. Итоговая формула для определения страхового тарифа будет выглядеть следующим образом:

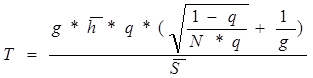
Расчет тарифных ставок во втором виде страхования предполагает множество допущений, а, следовательно, неточностей. Данный метод расчета требует соблюдения от страховщика множества условий, что подчас ему не под силу. Этот расчет можно считать как типовой, однако, его применение в других видах страхования, даже с небольшими отклонениями от рассмотренного, требует его корректировки. Кроме этого практический расчет и теоретическая его подоплека являются хорошим пособие при разработке методов-аналогов [10].

В страховании жизни и подобных, расчет тарифных ставок осуществляется на основании таблиц смертности – хорошо отработанных и проверенных статистических данных. Страхование жизни распространенный и давно практикуемый вид страхования в отличии от других видов, здесь объектом страхования является предмет, который есть у каждого – жизнь, здоровье, трудоспособность, что позволило создать точные данные для расчета. Поэтому методы, рассмотренные в данной работе, являются точным и пока единственным способом расчета страховых тарифов.

Основанием для расчета тарифных ставок служит вероятность наступления страхового события, которая является задающей величиной для расчета. На основании ее рассчитываются математические характеристики страхового события, законы его распределения, страховые аннуитеты и прочие данные.

Задача

Гражданин застраховал свою автогражданскую ответственность в страховой компании «ВСК». Срок договора с 1.06.02 по 31.12.02, агрегатный лимит ответственности страховщика на одно пострадавшее лицо за имущественный вред 4 тыс. р., за вред, причиненный личности третьего лица, 1 тыс. р. Лимит на одно страховое событие 7 тыс. р. Рассчитайте страховое возмещение за весь период, если гражданин был участником трех ДТП. В первом ДТП пострадало 4 человека и общий ущерб составил 13 тыс.р., во втором ДТП имущественный вред, причиненный автомобилю третьего лица, составил 22 тыс. р., а вред здоровью водителя этого транспортного средства 4 тыс. р. В третьем ДТП имущественный вред, причиненный автомобилю третьего лица, составил 4 тыс. р.

Решение:

1. За первое ДТП страховая выплата составила 4 чел. х 1 тыс. руб. = 4 тыс. руб.

2. За второе ДТП страховая выплата составила 4 тыс. руб. + 1 тыс. руб. = 5 тыс. руб.

3. За третье ДТП страховая выплата составила 4 тыс. руб.

4. Страховое возмещение за весь период составит 4 тыс. рую. + 5 тыс. руб. + 4 тыс. руб. = 13 тыс. руб.

Ответ: 13 тыс. руб.

Заключение

Страхование является одной из древнейших категорий общественно-производственных отношений. В большинстве цивилизованных стран мира в настоящее время страхование занимает одну из важнейших позиций в экономике. Страхование как процесс представляет собой соглашение между страховщиком и страхователем на основе договора или закона о защите имущественных интересов страхователя или застрахованного.

Взнос страхователя с единицы страховой суммы, который может быть выражен в рублях со страховой суммы или в процентах от нее носит название страховой тариф.

Страховая деятельность всегда подкрепляется законодательной базой. Основным юридическим документом, регламентирующим правовые отношения Сторон страхования является договор страхования.

В заключении хочется заметить, что предпосылками для дальнейшего развития страхового дела в нашей стране являются не только наметившаяся финансовая стабилизация и оживление экономики, но и становление источников такого развития. Во-первых, укрепление негосударственного сектора экономики: частный предприниматель в силу своей экономической обособленности от государства вынужден страховать свои риски. Во-вторых, источником спроса на страховые услуги является рост объемов и разнообразия частной собственности физических и юридических лиц. В-третьих, важным источником развития страхового рынка является сокращение некогда всеобъемлющих гарантий, предоставляемых системой государственного соцстрахования и соцобеспечения. И наконец в-четвертых, снятие «железного занавеса» между Россией и странами мира многократно увеличило поездки граждан за рубеж (круизы, туры, шопинг-туры и т.п.), что в свою очередь требует увеличения и качественного совершенствования страховых услуг, профессиональной подготовки кадров в области страхования. Но многое что еще требует кардинальных пересмотров особенно связанное с государственным страхованием.

Список литературы

1. Гвозденко А.А. Основы страхования: Учебник. – М.: Финансы и статистика, 2000. – 304с.

2. Гвозденко А.А. Финансово-экономические методы страхования: Учебник. –М.: Финансы и статистика, 2000. – 184с.

3. Зубец А.Н. Маркетинговые исследования страхового рынка. – М.: Центр экономики и маркетинга, 2001.–224с.

4. Основы страховой деятельности: Учебник/Отв. ред. проф. Т.А. Федорова. – М.: Издательство БЕК, 2001. – 768с.

5. Сербиновский Б.Ю., Гарькуша В.Н. Страховое дело: Учебное пособие для вузов. Серия «Учебники, учебные пособия». - Ростов н/Д: «Феникс», 2000. –384с.

6. Страхование: принципы и практика/Сост. Д. Бланд. – М.: Финансы и статистика, 2000. – 416с.

7. Шахов В.В. Страхование: Учебник для вузов. – М.: ЮНИТИ, 2000. – 311с.

8. Шинкоренко И.Э Страхование ответственности: Справочник. – М.: Финансы и статистика, 1999. – 286с.

9. Шихов А.К. Страхование: Учебное пособие для вузов. – М.: ЮНИТИ–ДАНА, 2001. – 431с.

10. Юлдашев Р., Тронин Ю. Концепция научной корректировки регулирования страховой деятельности//Страховое дело. – 2000. - №7. – С.16 – 46.

11. Юргенс И. Системный подход к определению понятия «национальная система страхования»//Страховое дело. – 2000. – №8. – С. 4 – 13.

Приложение 1

Таблица смертности

Таблица смертности и коммутационных функций. (мужчины, i=9%	Аннуитет.
x	lx	qx	dx	Dx	Nx	Cx	Mx	N(12)x	N(12)x	ax
18	100000	0,00149	149	21199,37402	244591,9762	28,978961	1003,702	254308,36	234875,5965	11,53769805
19	99851	0,001732582	173	19419,98803	223392,6022	30,868544	974,7228	232293,43	214491,7744	11,50323069
20	99678	0,001956299	195	17785,63423	203972,6142	31,921122	943,8543	212124,36	195820,8652	11,46839137
21	99483	0,002161173	215	16285,1745	186186,98	32,289068	911,9332	193651,02	178722,9417	11,4329128
22	99268	0,002337108	232	14908,238	169901,8055	31,965281	879,6441	176734,75	163068,8631	11,39650477
23	99036	0,002494043	247	13645,31729	154993,5675	31,22202	847,6788	161247,67	148739,4637	11,35873679
24	98789	0,002631872	260	12487,41769	141348,2502	30,151637	816,4568	147071,65	135624,8504	11,3192538
25	98529	0,002770758	273	11426,19487	128860,8325	29,045155	786,3051	134097,84	123623,8265	11,27766802
26	98256	0,002931119	288	10453,70243	117434,6376	28,111048	757,26	122225,92	112643,3573	11,23378424
27	97968	0,003123469	306	9562,441641	106980,9352	27,401825	729,1489	111363,72	102598,1494	11,18761706
28	97662	0,003327804	325	8745,480415	97418,49355	26,700225	701,7471	101426,84	93410,14836	11,13929583
29	97337	0,003564934	347	7996,676302	88673,01314	26,153784	675,0469	92338,156	85007,86983	11,08873359
30	96990	0,003814826	370	7310,246493	80676,33683	25,584698	648,8931	84026,866	77325,80719	11,03606245
31	96620	0,004046781	391	6681,063461	73366,09034	24,804406	623,3084	76428,244	70303,93625	10,98119944
32	96229	0,004250278	409	6104,611614	66685,02688	23,803942	598,504	69482,974	63887,07989	10,92371327
33	95820	0,004445836	426	5576,757172	60580,41527	22,74619	574,7001	63136,429	58024,40156	10,86301831
34	95394	0,004654381	444	5093,544793	55003,65809	21,749814	551,9539	57338,199	52669,11673	10,7986992
35	94950	0,004865719	462	4651,227061	49910,1133	20,762902	530,2041	52041,926	47778,3009	10,73052608
36	94488	0,00514351	486	4246,417888	45258,88624	20,038068	509,4412	47205,161	43312,61137	10,65813291
37	94002	0,005499883	517	3875,758159	41012,46835	19,556162	489,4031	42788,858	39236,0792	10,58179243
38	93485	0,005947478	556	3536,185269	37136,71019	19,294848	469,8469	38757,462	35515,95861	10,50191304
39	92929	0,006488825	603	3224,91182	33600,52492	19,198062	450,5521	35078,61	32122,44034	10,4190523
40	92326	0,007083595	654	2939,436635	30375,6131	19,102549	431,354	31722,855	29028,37131	10,33382137
41	91672	0,00770137	706	2677,628309	27436,17647	18,918722	412,2515	28663,423	26208,93016	10,24644697
42	90966	0,008310797	756	2437,621011	24758,54816	18,585848	393,3327	25875,791	23641,3052	10,15684885
43	90210	0,008879282	801	2217,763703	22320,92715	18,066191	374,7469	23337,402	21304,45212	10,06461018
44	89409	0,009428581	843	2016,579408	20103,16345	17,443562	356,6807	21027,429	19178,89788	9,968942143
45	88566	0,009969966	883	1832,62929	18086,58404	16,762616	339,2371	18926,539	17246,62895	9,869199483
46	87683	0,010572175	927	1664,548659	16253,95475	16,144862	322,4745	17016,873	15491,03661	9,76478198
47	86756	0,011261469	977	1510,963999	14589,40609	15,61071	306,3297	15281,931	13896,88092	9,655694043
48	85779	0,012077548	1036	1370,594794	13078,44209	15,186628	290,719	13706,631	12450,25281	9,542165305
49	84743	0,013027625	1104	1242,239788	11707,8473	14,847187	275,5323	12277,207	11138,48739	9,42478852
50	83639	0,014084339	1178	1124,822344	10465,60751	14,534292	260,6851	10981,151	9950,063933	9,304231523
51	82461	0,015219316	1255	1017,412812	9340,785164	14,205804	246,1508	9807,0994	8874,470959	9,18091954
52	81206	0,016365786	1329	919,2004449	8323,372352	13,801319	231,945	8744,6726	7902,072148	9,055013407
53	79877	0,017539467	1401	829,5018416	7404,171907	13,347725	218,1437	7784,3603	7023,983563	8,926046377
54	78476	0,018719099	1469	747,6631389	6574,670066	12,839982	204,796	6917,349	6231,991127	8,793626064
55	77007	0,01997221	1538	673,0895034	5827,006927	12,333106	191,956	6135,5063	5518,507571	8,657105626
56	75469	0,021359764	1612	605,1802003	5153,917423	11,85918	179,6229	5431,2917	4876,543165	8,516335169
57	73857	0,022936215	1694	543,3520131	4548,737223	11,43343	167,7637	4797,7736	4299,700884	8,371621184
58	72163	0,024694095	1782	487,0546557	4005,38521	11,034288	156,3303	4228,6186	3782,151826	8,223687348
59	70381	0,026654921	1876	435,8048455	3518,330554	10,657196	145,296	3718,0744	3318,586667	8,073179063
60	68505	0,028713233	1967	389,1637631	3082,525709	10,251513	134,6388	3260,8924	2904,158984	7,920896037
61	66538	0,030794433	2049	346,7794619	2693,361946	9,7971349	124,3873	2852,3025	2534,421359	7,76678622
62	64489	0,032966863	2126	308,3491604	2346,582484	9,3259673	114,5902	2487,9092	2205,255785	7,610147148
63	62363	0,035229222	2197	273,5631707	2038,233323	8,8416677	105,2642	2163,6164	1912,850203	7,450686137
64	60166	0,03749626	2256	242,1337182	1764,670153	8,3294577	96,42253	1875,6481	1653,692198	7,287998406
65	57910	0,040269384	2332	213,8115682	1522,536434	7,8991377	88,09308	1620,5334	1424,539466	7,120926372
66	55578	0,043092591	2395	188,2582643	1308,724866	7,4426939	80,19394	1395,0099	1222,439828	6,951752535
67	53183	0,046161367	2455	165,2713101	1120,466602	6,9992199	72,75124	1196,216	1044,717251	6,779559024
68	50728	0,049459864	2509	144,6258353	955,1952918	6,5625451	65,75203	1021,4821	888,9084507	6,604596544
69	48219	0,053028889	2557	126,1217074	810,5694566	6,1358661	59,18948	868,37524	752,763674	6,426882994
70	45662	0,056896325	2598	109,5721224	684,4477491	5,7194964	53,05361	734,66831	634,227193	6,246550074
71	43064	0,061071893	2630	94,80538649	574,8756268	5,3118756	47,33412	618,3281	531,423158	6,063744351
72	40434	0,065563635	2651	81,66554318	480,0702403	4,9121925	42,02224	517,50028	442,6401997	5,878491976
73	37783	0,0704285	2661	70,01032418	398,4046971	4,5235982	37,11005	430,49276	366,3166318	5,690656368
74	35122	0,075650589	2657	59,70605696	328,3943729	4,1438517	32,58645	355,75965	301,0290968	5,500185235
75	32465	0,081256738	2638	50,63234731	268,688316	3,7745132	28,4426	291,89481	245,4818234	5,30665336
76	29827	0,087370503	2606	42,67718158	218,0559687	3,4208503	24,66809	237,61634	198,4955938	5,109427581
77	27221	0,093898093	2556	35,73252729	175,3787871	3,07818	21,24724	191,7562	159,0013787	4,908099156
78	24665	0,100952767	2490	29,70395515	139,6462598	2,7510977	18,16906	153,26057	126,031947	4,701268201
79	22175	0,10854566	2407	24,50023732	109,9423046	2,4398114	15,41796	121,17158	98,71302919	4,487397537
80	19768	0,116653177	2306	20,03747055	85,44206731	2,1444354	12,97815	94,625908	76,25822663	4,264114429
81	17462	0,125415187	2190	16,2385651	65,40459675	1,8684061	10,83371	72,847272	57,96192108	4,027732522
82	15272	0,134821896	2059	13,02936001	49,16603165	1,6115991	8,965305	55,137822	43,19424165	3,773480171
83	13213	0,144857337	1914	10,34194219	36,13667164	1,3744094	7,353706	40,876728	31,3966148	3,494186195
84	11299	0,155677494	1759	8,113610993	25,79472944	1,1588134	5,979297	29,513468	22,07599107	3,179192282
85	9540	0,167180294	1594,9	6,284866394	17,68111845	0,9639503	4,820483	20,561682	14,80055469	2,813284697
86	7945,1	0,239053001	1899,3	4,801982189	11,39625206	1,0531452	3,856533	13,597161	9,195343554	2,373239135
87	6045,8	0,341625591	2065,4	3,352343059	6,594269868	1,0506846	2,803388	8,1307604	5,0577793	1,967062962
88	3980,4	0,488066526	1942,7	2,024859522	3,241926809	0,9066662	1,752703	4,1699874	2,313866194	1,601062579
89	2037,7	0,695048339	1416,3	0,951003092	1,217067286	0,6064157	0,846037	1,6529437	0,78119087	1,279772166
90	621,4	0,981670422	610,01	0,266064195	0,266064195	0,2396214	0,239621	0,3880103	0,144118106	1
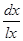
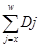
Формула				l_x*(1+i)^-x		d_x*(1+i)^-x+1
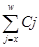
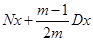
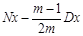
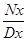