Оглавление

Введение……………………………………………………………………….3

1. Подбор экспертов и формирование экспертных групп………………….4

2. Формирование вопросов и составление анкет…………………………...7

3. Формирование правил определения суммарных оценок

    на основе оценок отдельных экспертов………………………………….7

4. Работа с экспертами……………………………………………………….9

5. Анализ и обработка экспертных оценок………………………………...10

Заключение…………………………………………………………………...15

Список использованной литературы……………………………………….16

Приложение………………………………………………………………….17

Введение

Несмотря на все большую роль математических методов при реше­нии экономических задач, нельзя считать, что формальные методы со­временной математики окажутся универсальным средством решения всех проблем, возникающих в сферах деятельности общества. Методы, ис­пользующие результаты опыта и интуицию, т.е. эвристические (неформальные), безусловно сохранят свое значение и в дальнейшем. Примерами традиционных, эвристических процедур являются раз­личные экспертизы, консилиумы, совещания и т.д. Порядок их проведе­ния часто регламентируется традицией, т.е. в конечном счете снова опы­том, и во многих отношениях представляет собой искусство. Однако по­степенно и в эту область начинают проникать разнообразные математи­ческие методы обработки исходного материала эвристического происхо­ждения, и в первую очередь статистические методы.

Можно выделить два уровня использования экспертных оценок: качественный и количественный. Если применение экспертных оценок на качественном уровне не вызывает сомнения, то возможность применения количественных балльных оценок нередко подвергается критике. При этом справедливо отмечают, что балльные оценки нередко скрывают неумение квалифици­рованно оценивать те или иные действия, явления, перспективы разви­тия.

Однако в связи с ограниченными возможностями применения в управлении и маркетинге экономико-математических методов, отсутстви­ем во многих случаях статистической и другой информации, а также на­дежных методов определения соответствия экономико-математических моделей реальным объектам экспертные оценки являются единственным средством решения многих задач. Для повышения достоверности и на­дежности получаемых с помощью экспертных оценок результатов надо владеть теоретическими и методическими основами использования дан­ных методов, избегать иллюзии простоты их применения.

1. Подбор экспертов и формирование экспертных групп

На первом этапе, исходя из целей экспертного опроса, решаются вопросы относительно структуры экспертной группы, количества экспер­тов и их индивидуальных качеств, иными словами, определяются направ­ления (разработка нового продукта, ценообразование, сбыт и т.п.), по ко­торым необходимо или желательно привлечь экспертов (устанавливается специализация экспертов). Далее по каждому направлению выделяются подгруппы экспертов и устанавливается количество экспертов в каждой подгруппе, которое зависит от конкретной постановки задачи и должно обеспечивать необходимый охват и полноту аспектов по каждому кон­кретному вопросу. Затем определяются требования к квалификации экс­пертов, стажу их работы в данной области опроса и общему стажу [2].

Определение численности экспертной группы можно осуществлять на основе показателей математической статистики или на основе «прагматического» подхода.

Зачастую расчеты по формулам математической статистики дают слишком высокие значения численности экспертной группы (порой больше 100 экспертов), поэтому на практике можно рекомендовать ис­пользовать «прагматический» подход, который не является столь теорети­чески обоснованным, как первый подход, но зато легко реализуемым.

Оценки численности группы экспертов в этом случае можно про­извести, руководствуясь следующими соображениями. Ясно, что числен­ность группы не должна быть малой, так как в этом случае был бы поте­рян смысл формирования экспертных оценок, определяемых группой специалистов. Кроме того, на групповые экспертные оценки в значи­тельной степени влияла бы оценка каждого эксперта. При увеличении группы экспертов хотя и устраняются эти недостатки, но зато появляется опасность возникновения новых. Так, при очень большом числе экспер­тов оценка каждого из них в отдельности почти не влияет на групповую оценку. Причем рост численности экспертной группы далеко не всегда приносит повышение достоверности оценок. Часто расширение группы экспертов возможно лишь за счет привлечения малоквалифицированных специалистов, что в свою очередь может привести лишь к уменьшению достоверности групповых оценок. Одновременно с ростом числа экспер­тов увеличиваются трудности, связанные с обработкой результатов опро­са и координацией работы группы. Следовательно, существуют некото­рые граничные оценки численности группы экспертов N_min и N_max, кото­рые определяются следующим образом.

Нижняя оценка численности N_min должна зависеть от числа оцени­ваемых событий. Данное предположение основано на существовании правила, которое обычно соблюдается при работе ученых советов, комис­сий специалистов и т.д., а именно - требований представительности группы, состоящей из N экспертов, для принятия решений по множеству m событий, которое можно представить как N ≥ m. Поэтому принимаем N_min ≥ m.

Верхней границей численности экспертной группы является по­тенциально возможное число экспертов:

N_max ≤ N_n,

откуда действительное значение численности группы N находится в пре­делах

т_тах ≤ N_min ≤ N ≤ N_max ≤ N_n.

После того как найдена численность группы, определяется ее структу­ра и состав, т.е. подбираются в группу эксперты требуемой специализации и квалификации. Для того чтобы экспертная группа могла всесторонне про­извести оценку событий, число экспертов Nι каждого ι-го направления желательно выбрать одинаковым:

         N

Nι = ----

         r

где ι =1,2,..., r;

r - число направлений [3].

Далее должно быть учтено одно ограничение, касающееся соответ­ствия целей экспертов целям экспертного опроса, т.е. необходимо уста­новить, имеется ли тенденция у отдельных экспертов необъективно оце­нивать рассматриваемые события. Для этого желательно выявить потен­циальные возможные цели экспертов, противоречащие целям получения объективных результатов. Анализируя предшествующую деятельность экспертов, необходимо выяснить наличие причин, которые приводят к стремлению завышать или занижать оценки так, чтобы повлиять на груп­повые в желательном для себя либо для других лиц направлении.

На основе сформулированных выше условий последовательность формирования группы экспертов может быть следующей. Сначала определяется потенциально возможное число экспертов N_n, а также минимально допустимая численность группы N_min. После этого среди потен­циально возможных экспертов выделяют группу специалистов N_k (N_k ≤ N_n) требуемой квалификации для оцениваемого класса событий. Затем из N_k исключают тех экспертов, чьи потенциально возможные цели могут противоречить целям получения объективных результатов. Из оставшихся экспертов N_u (N_u ≤ N_k) формируют группу так, чтобы в ней обеспечива­лось равночисленное представительство разных направлений. Для этого вначале определяют максимально возможное число представителей каж­дого направления как

               N_ц

N ι^max = ------

                r

Потом находят направление с наименьшим числом экспертов N ι^min, которое входит в группу N_u. Тогда общая численность группы бу­дет определяться по формуле

N = N ι^minr.

После этого проверяют соотношение N ≥ N_min. Если оно не удовле­творяется, то необходимо выяснить возможность ослабления приведенных выше ограничений либо допустимость нарушения условия N ≥ N_min, что связано с важностью принимаемых решений на основе экспертных оце­нок [2; 3].

 

 

 

2. Формирование вопросов и составление анкет

Правила опроса экспертов содержат ряд положений, обязательных к выполнению всеми. Эти правила должны обеспечивать соблюдение условий, благоприятствующих формированию экспертами объективного мнения. В число таких условий входит:

-  независимость формирования экспертами собственного мнения об оцениваемых событиях;

-  удобство работы с предполагаемыми анкетами (вопросы форму­лируются в общепринятых терминах и должны исключать всякую смы­словую неоднозначность и др.);

- логическое соответствие вопросов структуре объекта опроса;

-  приемлемые затраты времени на ответы по вопросам анкеты, удобное время получения вопросов и выдачи ответов;

-  сохранение анонимности ответов для членов экспертной груп­пы;

-  проведение коллективных обсуждений оцениваемых событий;

-  предоставление экспертам требуемой информации [1; 3].

Для обеспечения выполнения этих условий должны быть разрабо­таны правила проведения опроса и организации работы экспертной груп­пы. Причем в них должна быть учтена специфика оцениваемых событий, а также особенности организаций, из которых приглашаются эксперты.

3. Формирование правил определения суммарных оценок на основе оценок отдельных экспертов

Если имеются оценки а_ij событий (факторов) C_i, определенные ка­ждым             n_j є N экспертом, то возникает вопрос о том, каким образом могут быть получены групповые оценки событий.

В общем случае групповая оценка a_i каждого C_i события зависит от оценок экспертами этого события и степени компетентности h_j экспер­тов. Степень компетентности h_j эксперта учитывает его опыт и квалифи­кацию и является основной характеристикой эксперта, которая использу­ется при определении групповых оценок. Поэтому

a_i = f (a_ij, h_j)

где i = 1, 2,..., m;

      j = 1, 2,..., p.

Следовательно, задание способа формирования групповых экс­пертных оценок состоит в определении этой функции. Причем необхо­димо, чтобы она была строго монотонно возрастающей по а_ij и h_j.

Этому условию удовлетворяет множество функций. Обычно пола­гают, что функцию (1) можно представить как

            p

           Σh_j a_ij

           j=1

a_i = ------------------.

             p

            Σh_j

            j=1

При равной компетентности экспертов эта формула принимает вид средней оценки

            p

           Σ a_ij

           j=1

a_i = ------------------.

             p

В зависимости от специфики экспертного опроса, объекта исследо­вания и используемой методики обработки экспертных данных оценки а_ij могут иметь различную шкалу измерения: от 0 до 1, от 0 до 10 и от 0 до 100. Принципиальной разницы в данных шкалах нет, выбор той или иной из них во многом определяется удобством получения и обработки оценок, а также вкусом исследователя, проводящего экспертный опрос [3].

Для того чтобы учитывать различие в компетентности экспертов, им могут быть приписаны различные «веса», которые учитываются при определении групповых оценок. Причем значения этих коэффициентов интерпретируются как вероятность задания экспертом достоверной оцен­ки. Тогда 0 < h_j ≤ 1. Значения весовых коэффициентов могут быть ис­пользованы при построении системы стимулирования работы группы экспертов. Например, дополнительная оплата за работу по оценке собы­тий определится пропорционально весовому коэффициенту эксперта.

4. Работа с экспертами

В зависимости от характера исследуемого объекта, от степени его формализации и возможности привлечения необходимых экспертов по­рядок работы с ними может быть различным, но в основном он содержит следующие три этапа.

На первом этапе эксперты привлекаются в индивидуальном поряд­ке с целью уточнить модель объекта, ее параметры и показатели, подле­жащие экспертной оценке; уточнить формулировки вопросов и термино­логию в анкетах; согласовать целесообразность представления таблиц экспертных оценок в той или иной форме; уточнить состав группы экс­пертов.

На втором этапе экспертам направляются анкеты с пояснительным письмом, в котором описывается цель работы, структура и порядок за­полнения анкет с примерами.

Когда имеется возможность собрать экспертов вместе, особенно если удается их сгруппировать в соответствии с какими-либо признаками, существенно важными для данного опроса, например эксперты из одной организации, только сотрудники сбытовых служб, то цели и задачи анке­тирования, а также все вопросы, связанные с анкетированием, могут быть доложены устно. Обязательное условие такой формы экспертного опроса - последующее самостоятельное заполнение анкет при соблюде­нии всех правил анкетирования.

Третий этап работы с экспертами осуществляется после получения результатов опроса и изучения исследуемого объекта другими методами в процессе обработки и анализа полученных результатов. На этом этапе от экспертов в форме консультаций обычно получают всю недостающую информацию, которая требуется для уточнения полученных данных и их окончательного анализа [5].

5. Анализ и обработка экспертных оценок

При проведении анализа собранных экспертных данных в соответ­ствии с целями исследования и принятыми моделями необходимо опре­делить согласованность действий экспертов и достоверность экспертных оценок.                               

Пусть для каждого события C_i на основании оценок а_ij, заданных группой из Р экспертов, образована матрица рангов важности - || а_ij ||, где i = 1, 2,..., m - число событий, j = 1, 2,..., р - число экспертов. Мат­рица || α_ij ||  получается из матрицы || а_ij || путем определения, исходя из ко­эффициентов относительной важности событий а_ij рангов важности этих событий, т.е. событиям присваиваются номера 1, 2, 3,..., m натурального ряда чисел.

Таким образом, при ранжировании события располагаются в по­рядке возрастания или убывания какого-либо признака X, количественно неизмеримого. Ранг a_i указывает то место, которое занимает i-e событие среди других m событий, ранжированных в соответствии с признаком X.

Ранжирование применяется, когда события располагаются согласно неизмеримому и неподсчитываемому качеству или рассматриваются только относительно взаимного расположения во времени или пространстве. Ранжирование может являться менее точным вы­ражением упорядоченной связи событий относительно какого-либо изме­римого или подсчитываемого качества как замена переменной порядко­вым номером в прикидочных расчетах в целях экономии времени и уменьшения трудоемкости вычислений [4].

При использовании рангов важности для сравнения результатов (событий) нельзя установить, насколько один результат лучше другого, можно только определить ряд предпочтения рассматриваемых результа­тов. Иными словами, числа, характеризующие порядковую меру предпоч­тительности результатов, при сравнении, предположим, событий А и Б нельзя делить или вычитать, пытаясь узнать, насколько первый результат лучше второго.

Будем рассматривать упорядоченную последовательность суммар­ных рангов m событий, которую представим в виде

α₁ < α.₂ <... α_i, <... <α_m,         (1)

где α_i находится из матрицы || а_ij ||  по формуле

       p

a_i = Σ а_ij

      j=1

В табл. 1 приводится условный пример определения рангов важ­ности событий исходя из их коэффициентов относительной важности (более важное событие имеет меньший ранг важности) [3].

Таблица 1

Определение рангов важности

	События С
1	2	3
Оценки экспертов аij	эксперт j = 1	0,5	0,2	0,3
эксперт j = 2	0,3	0,6	0,1
Ранги важности ajj	эксперт j = 1	1	3	2
эксперт j = 2	2	1	3
Суммарный ранг важности αi	3	4	5

Среднее значение для суммарных рангов рассматриваемого ряда

p        p               p               p

Σα_1j , Σα_2j , … ,  Σα_ij , . . . , Σα_ij

 j=1    j=1

равно

       1

α = -- p(m +1).

       2

Суммарное квадратическое отклонение S суммарных событий от среднего значения а есть

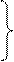
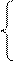      m     p       1                 2

S = Σ     Σα_ij - --p(m+1)

                       2

      i=1   j=1

Величина S достигает максимального значения в случае, если все р экспертов дадут одинаковые оценки каждому C_i событию.

Тогда рассматриваемый ряд суммарных рангов будет иметь вид р, 2р,..., mр.

Вычтем из этого ряда среднее значение:

       1                  1                 1                     1

α = --- p (m+1); --- p (1-m); --- p (3-m)… ---p (m-1).

       2                  2                 2                     2

Сумма квадратов этого ряда равняется

            1

S_max = --- p²(m³-m).

           12

Очевидно, что в качестве меры согласованности экспертов можно принять отношение

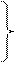                      m      p        1                2

                       Σ     Σ α_ij - --- p(m+1)

           S         i=1  j=1       2

W = ------ = ---------------------------------,

         S_max         1                  

                       ---- mp²(m²-1)

                        12                 

называемое коэффициентом конкордации. Величина W изменяется в пределах от 0 до 1. При W = 0 согласованности совершенно нет, т.е. связь между оценками различных экспертов отсутствует. Наоборот, при W = 1 согласованность мнений экспертов полная [2; 3].

В том случае, если последовательность (1) кроме строгих нера­венств имеет равенства, т.е. существует совпадение рангов, то формула для вычисления коэффициента конкордации имеет вид

                         S

W = -----------------------------------

              1                       p

            ---- mp²(m²-1)-pΣT_j

            12                     j=1

                        1

где T_i = --- Σ (t_j³ – t_i);

             12  k_j

       t_j - число повторений каждого ранга в j-м ряду;

       k_j - число повторяющихся рангов в j-м ряду.

Когда ранги повторяются, то для получения нормальной ранжи­ровки, имеющей среднее значение ранга, равное

1

-- p (m+1),

2

необходимо приписать событиям, имеющим одинаковые ранги, ранг, равный среднему значению мест, которые эти события поделили между собой [3].

Например, получена следующая ранжировка событий:

События i	1	2	3	4	5	6
Ранги αi	1	2	3	3	2	3

События 2 и 5 поделили между собой второе и третье места. Зна­чит, им приписывается ранг

 2+3

------ = 2,5

   2

события 3, 4 и 6 поделили между собой четвертое, пятое, шестое места, и им приписывается ранг

4+5+6

-------- = 5.

   3

Таким образом, получаем нормальную ранжировку:

События i	1	2	3	4	5	6
Ранги αi	1	2,5	5	5	2,5	5

Пример. Рассмотрим ранжирование m = 10 событий р = 3 экспер­тами: N, Q, R. Результаты расчетов представлены в приложении 1.

S = 591;

                                                           1

T_N = --- x 2(2³ – 2) = 1;

                                                         12

       1                          1

T_q = --- x 3(2³ – 2) = 1---;

      12                         2

                                                       1

T_R = --- x (4³ – 4,3³ – 3) = 7.

                                                      12

Для крайних значений коэффициента конкордации могут быть вы­сказаны следующие предположения. Если W = 0, то согласованности в оценках нет, поэтому для получения достоверных оценок следует уточ­нить исходные данные о событиях и (либо) изменить состав группы экс­пертов. При W = 1 далеко не всегда можно считать полученные оценки объективными, поскольку иногда оказывается, что все члены экспертной группы заранее сговорились, защищая свои общие интересы.

Необходимо, чтобы найденное значение W было больше заданного значения W₃ (W > W₃). Можно принять W₃ = 0,5, т.е. при W > 0,5 дейст­вия экспертов в большей степени согласованы, чем не согласованы. При W < 0,5 полученные оценки нельзя считать достоверными, и поэтому следует повторить опрос заново. Жесткость данного утверждения опреде­ляется важностью проводимого исследования и возможностью повторной экспертизы. Практика показывает, что очень часто этим требованием пренебрегают.

Заключение

В ходе работы было выявлено, что методы экспертных оценок используются для прогнозирования событий будущего, если отсутствуют статистические данные или их недостаточно. Они также применяются для количественного измерения таких событий, для которых не существует других способов измерения.

Предполагается, что эксперт основывает свое суждение на группе причинных факторов, действующих в рамках определенного сценария, оценивая вероятность их реализации и их вероятное влияние на изучаемый показатель.

При этом данная казуальная структура неразрывно связана с личностью эксперта, так что другой эксперт, поставленный перед той же проблемой, может, используя ту же информацию, прийти к другим выводам.

Основными этапами экспертных опросов являются:

1. Подбор экспертов и формирование экспертных групп.

2. Формирование вопросов и составление анкет.

3. Формирование правил определения суммарных оценок на основе оценок отдельных экспертов.

4. Работа с экспертами.

5. Анализ и обработка экспертных оценок.

Последний этап является наиболее трудоемким и требует тщательного подхода при его проведении, так как от правильности анализа и обработки данных зависит достоверность исследования.

При проведении обработки данных используют ранжирование событий. При этом ставится цель определить согласованность действий экспертов и достоверность экспертных оценок.

Список использованной литературы

1. Бешелев С.Д. Математико-статистические методы экспертных оценок. – М.: Статистика, 1980. – 263с.

2. Голубков Е.П. Использование системного анализа в принятии плановых решений. – М.: Экономика, 1982. – 160с.

3. Голубков Е.П. Маркетинговые исследования: теория, методология и практика. – М.: Финпресс, 1998. – 416с.

4. Плотинский Ю.М. Теоретические и эмпирические модели социальных процессов. – М., 1998. – 280с.

5. Ядов В.А. Социологическое исследование: методология, программа, методы. – Самара: Изд-во «Самарский университет», 1995. – 331с.