ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ

РЕГИОНАЛЬНАЯ КАФЕДРА МАТЕМАТИКИ И ИНФОРМАТИКИ

ЛАБОРАТОРНАЯ РАБОТА

по дисциплине «Экономико-математические методы и прикладные модели»

Вариант 9

Уфа-2008

Содержание

1.Задача линейного программирования. 3

2. Задача о назначениях. 10

3. Анализ временных рядов и прогнозирование экономических процессов. 21

Окно «Обработка временных рядов» (Рис. 3.3). 22

1.Задача линейного программирования

Задача об оптимальном использовании ограниченных ресурсов

1.9 Продукцией городского молочного завода являются молоко, кефир и сметана. На производство 1 т молока, кефира и сметаны требуется соответственно 1,01; 1,01 и 9,45т молока. При этом затраты рабочего времени при разливе 1т молока и кефира составляют 0,18 и 0,19 машиночаса. На расфасовке 1т сметаны заняты специальные автоматы в течение 3,25 ч. Всего для производства цельномолочной продукции завод может использовать 136т молока. Основное оборудование может быть занято в течение 21,4 машиночасов, а автоматы по расфасовке сметаны – в течение 16,25 ч. Прибыль от реализации 1т молока, кефира и сметаны соответственно равна 30, 22 и 136 руб. Завод должен ежедневно производить не менее 100т молока.

Требуется определить объемы выпуска молочной продукции, позволяющие получить наибольшую прибыль. К чему приведет задание по выпуску кефира в объеме не менее 10т?

Экономико-математическая модель

Ресурсы	Норма расхода ресурсов	Наличие ресурсов
Молоко	Кефир	Сметана
Сырье (т)	1,01	1,01	9,45	136
Основное оборудование (машиночас)	0,18	0,19	-	21,4
Автоматы (ч)	-	-	3,25	16,25
Цена (тыс. руб.)	30	22	136

Обозначим через Х₁, Х₂, Х₃ объемы производства соответствующего вида продукции.

F(x) = 30x₁ + 22x₂ + 136x₃→max

Ограничения по ресурсам:

1,01Х₁ + 1,01Х₂,+ 9,45Х₃ ≤ 136

0,18Х₁ + 0,19Х₂ + 0Х₃ ≤ 21,4

0Х₁ + 0Х₂ + 3,25Х₃ ≤ 16,25

Х₁ ≥ 100

Х₂ ≥ 0

Х₃ ≥ 10.

Решение. Проведем подробное описание технологии получения решения проведенной ЗЛП.

1. Создать форму для ввода условий задачи (Рис. 1.1).

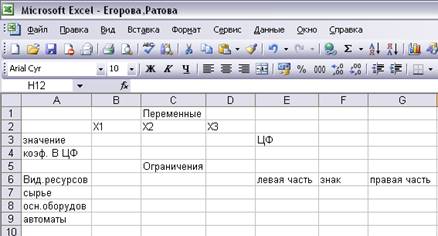
Рис. 1.1 Таблица для ввода условий задачи

2. Указать адреса ячеек, в которых будет помещен результат решения (изменяемые ячейки). Обозначим через Х₁, Х₂, Х₃  объем производства каждого вида продукции. В нашей задаче оптимальные значения компонент вектора Х = (Х₁, Х₂, Х₃) будут помещены в ячейках В3:D3, оптимальное значение целевой функции – в  ячейке Е4.

3. Ввести исходные данные задачи в созданную форму – таблицу, представленную на Рис. 1.2.

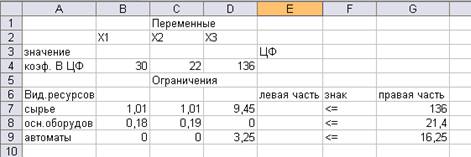
Рис. 1.2 Таблица с исходными данными

4. Введем зависимость для целевой функции:

-       Курсор в ячейку Е4;

-       Курсор на кнопку «Мастер функций», расположенную на панели инструментов;

-       На экране появляется диалоговое окно Мастер функций шаг 1 из 2 (Рис. 1.3)

Рис. 1.3 Мастер функций шаг 1 из 2

-  Курсор в окно «Категория» на категорию Математические;

-  Курсор в окно Функции на СУММПРОИЗВ;

-  На экране появится диалоговое окно СУМПРОИЗВ (Рис. 1.4);

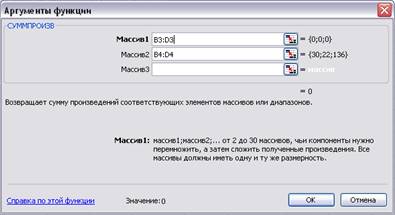
Рис. 1.4 Ввод ограничений для функции

-       В строку «Массив 1» ввести В3:D3;

-       В строку «Массив 2» ввести В4:D4;

-       На экране в строке Е4 введена функция (Рис. 1.5)

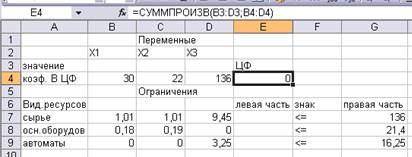
Рис. 1.5 Функция СУММПРОИЗВЕД

5. Ввести зависимость для ограничений:

-       Курсор в ячейку Е4;

-       Значения ячейки Е4 копировать в ячейки Е7, Е8, Е9.

В строке Меню указатель мыши на имя Сервис. В развернутом меню команда Поиск решения. Появляется диалоговое окно Поиск решения  (Рис. 1.6).

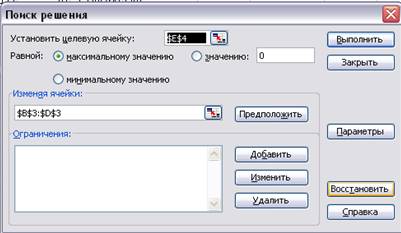
Рис. 1.6 Поиск решения

6. Назначить целевую функцию (установить целевую ячейку):

-       Курсор в строку установить целевую ячейку;

-       Введите адрес ячейки $F$4;

-       Введите направление целевой функции в зависимости от условия задачи – Максимальному значению;

-       Курсор в строку Изменяя ячейки;

-       Введите адрес искомых переменных $B$3:$D$3.

7. Ввести ограничения:

-       Указатель мышки на кнопку Добавить. Появляется диалоговое окно Добавление ограничения (Рис. 1.7);

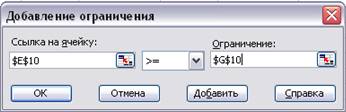
Рис. 1.7 Добавление ограничений

-       В строке Ссылка на ячейку введите адрес $E$10;

-       Введите знак ограничения  ≤;

-       В строке Ограничение введите адрес  $G$10;

-       Указатель мыши на кнопку Добавить. На экране вновь диалоговое окно Добавление ограничения.

-       Введите остальные ограничения задачи, по вышеописанному алгоритму;

-       После введения последнего ограничения кнопка ОК.

На экране появится диалоговое окно Поиск решения с введенными условиями (Рис. 1.8)

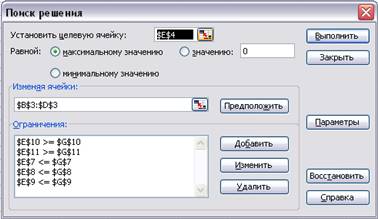
Рис. 1.8 Поиск решения

8. Ввести параметры для решения ЗЛП:

-       В диалоговом окне указатель мыши на кнопку Параметры. На экране появляется диалоговое окно Параметры поиска решения (Рис. 1.9);

Рис. 1.9 Параметры поиска решения

-       Установите флажки в окнах Линейная модель (это обеспечит применение симплекс-метода) и Неотрицательные значения;

-       Указатель мыши на кнопку ОК. На экране диалоговое окно Поиск решения;

-       Указатель мыши на кнопку Выполнить.

Через непродолжительное время появится диалоговое окно Результаты поиска решения и исходная таблица с заполненными ячейками В3:D3 для значений X_i и ячейка F4 с максимальным значением целевой функции (Рис. 1.10)

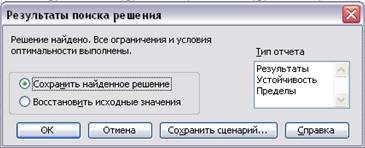
Рис. 1.10 Результат поиска решения

Полученное решение означает, что максимальный доход 3707,22 тыс. руб. городской молочный завод может получить при выпуске и реализации 108,33 т молока, 10т кефира и 1,74 т сметаны. При этом ресурсы и фонды будут использованы полностью, а из 16,25 ч на расфасовку сметаны будет использовано только 5,66 ч (Рис. 1.11)

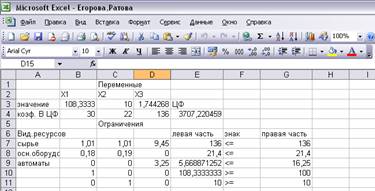
Рис. 1.11 Итоговая таблица

2. Задача о назначениях

2.9  Мастер должен назначить на 10 типовых операций 12 рабочих. Данные о времени, которое затрачивают рабочие на выполнение каждой операции, приведены ниже в таблице 2.1 (матрица эффективности назначений).

Операция Рабочий	О1	О2	О3	О4	О5	О6	О7	О8	О9	О10
Р1	29	31	16	16	17	34	20	28	16	13
Р2	29	25	22	30	24	31	37	23	16	27
Р3	27	32	0	14	34	30	27	16	19	17
Р4	21	35	0	32	31	28	30	29	31	16
Р5	21	36	0	14	24	30	21	28	29	27
Р6	28	35	25	30	22	16	0	18	25	18
Р7	27	34	33	26	14	19	18	37	19	16
Р8	27	34	27	30	37	37	26	22	35	33
Р9	16	26	18	26	16	20	31	34	28	29
Р10	16	22	33	22	21	19	19	37	36	24
Р11	26	35	13	14	17	36	17	17	25	21
Р12	34	25	19	14	36	36	17	36	26	33

Рис. 2.1 Матрица эффективности назначений

В матрице эффективностей назначений проставлен запрет «-», если рабочий не может выполнять соответствующую операцию.

Сформировать план назначения рабочих по операциям, при котором суммарное время на выполнение работ будет минимальным.

Экономико-математическая модель

Назначение целевой функции:       

           _{m m}

F =  SS C_ijx_ij→min, x_ij ≥ 0,  i = 1,……, m

         ^{j=1 i=1}            

при ограничениях:

          _m

S x_ij ≤1, I = 1,2,3,4,5,6,7,8,9,10 (условия назначения работника)

         ^j=1

 _m

S x_ij = 1, j = 1,2,3,4,5,6,7,8,9,10,11,12 (условия заполнения вакантной

ⁱ⁼¹                                                                                                                                                должности)      

Рассмотрим более подробно каждый из этих этапов:

1. Создание формы для решения задачи предполагает создание матрицы назначений по должностям.

Для этого необходимо выполнить резервирование изменяемых ячеек: B3:K15 вводятся «1».

Таким образом, резервируется место, где после решения задачи будет находиться распределение рабочих по должностям, обеспечивающее максимальную производительность труда.

2. Ввод граничных условий.

Введите условия назначения работника только на одну должность, т.е.

       _m

S x_ij ≤1, i = 1,…..,m

     ^j=1

где    x_ij - назначение  i-го работника на j-ую должность,

m – количество вакантных должностей.

Для этого необходимо выполнить следующие операции:

-       Курсор в ячейку  А3;

-       Щелкнуть знак «S»;

-       Выделите необходимые для суммирования ячейки B3:K3;

-       Нажать ENTER – подтверждение ввода формул для суммирования.

Аналогичные действия ввести выполнить для ячеек А4, А5, А6, А7, А8, А9, А10, А11, А12, А13, А14, т.е. ввести условия условия заполнения вакантной должности (для всех строк). Эти действия можно реализовать иначе:

-       Курсор в ячейку А3;

-       Копировать в буфер (т.е. копировать в буфер формулу, введенную для ячейки А3);

-       Выделить ячейки А4:А14;

-       Вставить из буфера (вставка формула для суммирования в А4:А14).

Введение условия заполнения вакантной должности, т.е.

_m

S x_ij = 1, j = 1,…,m.

ⁱ⁼¹            

Для этого необходимо выполнить следующие операции:

-       Курсор в В15;

-       Щелкните знак «S». При этом автоматически выделяется весь столбец В3:В14;

-       ENTER – подтверждение суммирования показателей выделенного столбца.

-       Последовательность этих действий выполнить для ячеек С15:К15.

Таким образом, введены ограничения по назначению работника только на одну должность и условию заполнения всех вакантных мест.

3. Ввод исходных данных.

Ввод условных операций(в ячейке А19:А30 вводится «1»), потребность в заполнении вакантной должности («1» - в В18:К18), ввод затрачиваемого времени на выполнение каждой операции (блок В19:К30лок д затрачиваемого времени на выполнение каждой операции ()полнения всех вакантных мест.

рабочих по должностям               ) (Рис. 2.2)

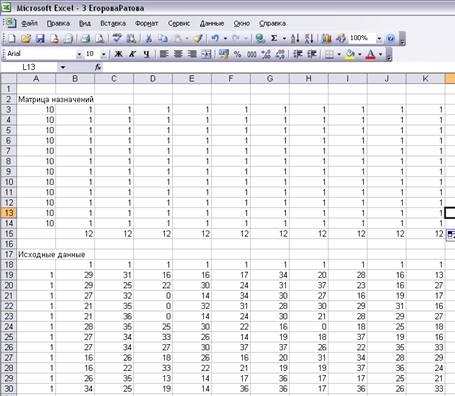
Рис. 2.2 Ввод исходных данных

4. Назначение целевой функции.

Для вычисления значения целевой функции, соответствующей максимальной суммарной производительности труда, необходимо зарезервировать ячейку и ввести формулу для ее вычисления:

           _{m m}

F =  SS C_ijx_ij,

         ^{j=1 i=1}

где C_ij – производительность труда i-го ратника при занятии j-ой должности;

x_ij – назначение i-го работника на j-ую должность.

Для этого:  

-       Курсор в ячейку В32. В данную ячейку будет помещаться значение целевой функции после решения задачи;

-       Щелкнуть Мастер функций:

-       В окне Категория выбрать Математические;

-       В окне Функция при помощи спинера выбрать СУММПРОИЗВ;

-       ОК;

-       В окне СУММПРОИЗВ указать адрес массивов, элементы которого обрабатываются этой функцией.

В задаче целевая функция представляет собой произведение производительности труда работников (расположенных в блоке ячеек В19:К30) и назначения работников на должности (содержимое ячеек В3:К14). Для этого:

-       В поле Массив 1 указать адреса В19:К30;

-       В поле Массив 2 указать адреса В3:К14;

-       ОК – подтверждение окончания ввода адресов вне массивов.

В поле ячейки В32 появится некоторое числовое значение, равное произведению «1» на производительность каждого работника на ой должности (число 67 в данной задаче) (Рис. 2.3)

Рис. 2.3 Назначение целевой функции

5. Ввод зависимостей из математической модели.

Для осуществления этого этапа необходимо выполнить следующий перечень операций:

-       Щелкнуть Сервис – Поиск решения;

-       Курсор подвести в поле Установить целевую (ячейку);

-         Ввести адрес $B$32. Таким образом производится указание ячейки, куда при решении задачи помещается значение целевой функции (или же: курсор в ячейку В32, затем щелкнуть Поиск решения. При этом осуществиться автоматический ввод адреса $B$32 в поле адреса целевой ячейки);

-         Установит направление изменения целевой функции, равное «максимальному значению»;

-       Ввести адрес изменяемых ячеек В3:К14. Для этого:

o   Щелкнут в поле Изменяя ячейки;

o   Ввести адреса $B$3:$K$14 (или же щелкнуть на маленькой красной стрелке рядом с этим полем, выйти в таблицу с матрицей перевозок, выделить блок ячеек В3:К14, щелкнуть на красной стрелке и вернуться в блок Поиск решения, при этом нужные адреса будут выделены).

-         Ввести ограничение задачи. В матрицу перевозок, содержащую исходные данные по задаче, необходимо ввести условие назначения работника только на одну должность. Для этого:

o   Щелкнуть Добавить ограничения;

o   В поле Ссылки на ячейку ввести адрес $А$3:$А$14;

o    В среднем поле установить знак «≤». Для этого щелкнуть спинер и выбрать необходимый знак «≤»;

o   В поле Ограничение установить 1;

o    Щелкнуть ОК, т.е. осуществить подтверждение введенного условия. После этого Вы вернетесь в поле Поиск решения.

Далее вводится ограничение, которое реализует условие заполнения вакантной должности. Для этого:

o   Щелкнуть Добавить ограничение;

o   В поле Ссылка на ячейку ввести адрес $B$15:$K$15;

o   В поле знака выбрать  при помощи спинера знак «=»;

o   В поле Ограничения установить 1;

o   ОК (Рис. 2.4)

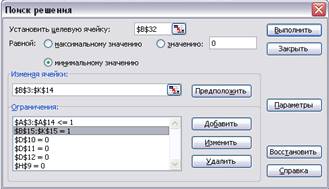
Рис. 2.4 Ввод зависимостей из математической модели

6. ввод ограничений.

Далее необходимо установить ограничения на решение задачи. Для этого:

-       Щелкнуть Параметры;

-       Установить Линейная модель;

-       Установить неотрицательные значения (назначение работника на должность принимает значение «1» или «0», т. е. отрицательной величиной быть не может);

-       ОК. После этого осуществиться выход в поле Поиск решения;

-       Нажать выполнить.

7. Просмотр результатов и печать отчета.

После выполнения всех вышеуказанных действий на экран выводится окно Результаты поиска решения.

-       В окне Тип отчета выбрать интересующий вид отчета;

-       ОК;

-         Внизу страницы экрана содержится сообщение Отчет по результатам 1(Рис. 2.5) Щелкнуть на этом сообщении, на экран выводятся результаты решения задачи, которые можно распечатать.

При нажатии Лист 1 происходит возврат в программу к исходным данным.

В Матрице назначений содержится схема распределения работников по должностям (1 – назначен, 0 – не назначен), дающая максимальную суммарную производительность труда. Значение целевой функции содержится в ячейке В32 и для конкретной задачи равно 133 (Рис. 2.6)

Microsoft Excel 9.0 Отчет по результатам
Рабочий лист: [3 ЕгороваРатова.xls]Лист3
Отчет создан: 01.12.2007 19:28:20
Целевая ячейка (Минимум)
	Ячейка	Имя	Исходно	Результат
	$B$32		275	133
Изменяемые ячейки
	Ячейка	Имя	Исходно	Результат
	$B$3		0	0
	$C$3		0	0
	$D$3		0	0
	$E$3		0	0
	$F$3		0	0
	$G$3		0	0
	$H$3		2,67908E-12	0
	$I$3		0	0
	$J$3		1	9,16822E-13
	$K$3		1,33937E-12	1
	$B$4		0	0
	$C$4		0	0
	$D$4		0	0
	$E$4		0	0
	$F$4		0	0
	$G$4		1	0
	$H$4		0	0
	$I$4		2,67908E-12	0
	$J$4		0	1
	$K$4		0	0
	$B$5		0	0
	$C$5		0	0
	$D$5		0	0
	$E$5		0	0
	$F$5		1,33948E-12	0
	$G$5		0	0
	$H$5		1	0
	$I$5		0	1
	$J$5		0	1,12959E-11
	$K$5		0	0
	$B$6		0	0
	$C$6		0	0
	$D$6		0	1
	$E$6		1	0
	$F$6		0	0
	$G$6		1,33948E-12	0
	$H$6		0	0
	$I$6		0	0
	$J$6		0	0
	$K$6		0	0
	$B$7		0	0
	$C$7		0	0
	$D$7		0	0
	$E$7		0	1
	$F$7		1	0
	$G$7		0	0
	$H$7		0	0
	$I$7		0	0
	$J$7		0	0
	$K$7		0	0
	$B$8		1	0
	$C$8		1,33948E-12	0
	$D$8		0	0
	$E$8		2,22045E-16	0
	$F$8		0	0
	$G$8		0	0
	$H$8		0	1
	$I$8		0	0
	$J$8		0	0
	$K$8		0	0
	$B$9		8,81184E-13	0
	$C$9		0	0
	$D$9		1	0
	$E$9		0	0
	$F$9		0	1
	$G$9		0	6,673E-12
	$H$9		0	0
	$I$9		0	0
	$J$9		0	0
	$K$9		0	0
	$B$10		0	0
	$C$10		1	0
	$D$10		0	0
	$E$10		0	0
	$F$10		0	0
	$G$10		0	0
	$H$10		0	0
	$I$10		0	0
	$J$10		0	0
	$K$10		0	0
	$B$11		2,22045E-16	1
	$C$11		0	0
	$D$11		0	0
	$E$11		0	0
	$F$11		0	0
	$G$11		0	7,78366E-12
	$H$11		0	0
	$I$11		0	0
	$J$11		0	0
	$K$11		0	0
	$B$12		0	0
	$C$12		0	1,18251E-11
	$D$12		0	0
	$E$12		0	0
	$F$12		0	0
	$G$12		0	1
	$H$12		0	0
	$I$12		0	0
	$J$12		0	0
	$K$12		0	0
	$B$13		0	0
	$C$13		0	0
	$D$13		0	0
	$E$13		0	9,99179E-12
	$F$13		0	9,77463E-12
	$G$13		0	0
	$H$13		0	1,04146E-11
	$I$13		1	0
	$J$13		3,13738E-12	0
	$K$13		0	0
	$B$14		0	0
	$C$14		0	1
	$D$14		0	0
	$E$14		0	0
	$F$14		0	0
	$G$14		0	0
	$H$14		0	0
	$I$14		0	0
	$J$14		0	0
	$K$14		1	0
Ограничения
	Ячейка	Имя	Значение	формула	Статус	Разница
	$B$15		1	$B$15=1	не связан.	0
	$C$15		1	$C$15=1	не связан.	0
	$D$15		1	$D$15=1	не связан.	0
	$E$15		1	$E$15=1	не связан.	0
	$F$15		1	$F$15=1	не связан.	0
	$G$15		1	$G$15=1	не связан.	0
	$H$15		1	$H$15=1	не связан.	0
	$I$15		1	$I$15=1	не связан.	0
	$J$15		1	$J$15=1	не связан.	0
	$K$15		1	$K$15=1	не связан.	0
	$A$3	Матрица назначений	1	$A$3<=1	связанное	0
	$A$4	Матрица назначений	1	$A$4<=1	связанное	0
	$A$5	Матрица назначений	1	$A$5<=1	связанное	0
	$A$6	Матрица назначений	1	$A$6<=1	связанное	0
	$A$7	Матрица назначений	1	$A$7<=1	связанное	0
	$A$8	Матрица назначений	1	$A$8<=1	связанное	0
	$A$9	Матрица назначений	1	$A$9<=1	связанное	0
	$A$10	Матрица назначений	0	$A$10<=1	не связан.	1
	$A$11	Матрица назначений	1	$A$11<=1	связанное	0
	$A$12	Матрица назначений	1	$A$12<=1	связанное	0
	$A$13	Матрица назначений	3,0181E-11	$A$13<=1	не связан.	1
	$A$14	Матрица назначений	1	$A$14<=1	связанное	0
	$H$9		0	$H$9=0	не связан.	0
	$D$12		0	$D$12=0	не связан.	0
	$D$11		0	$D$11=0	связанное	0
	$D$10		0	$D$10=0	связанное	0

Рис. 2.5 Отчет по результатам

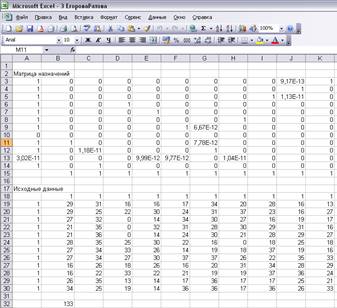
Рис. 2.6 Задача решена

3. Анализ временных рядов и прогнозирование экономических процессов

1.     Создать файл исходных данных по своему варианту в среде Microsoft Excel-2000

1.1.                    Для этого инсталировать (запустить) программу Microsoft Excel-2000.

1.2.                    Ввести данные (шаблон). Для этого в ячейке А1 записать «ВРЕМЯ»; в ячейке А2 «ПОКАЗАТЕЛЬ» и далее числовые данные о времени и уровнях моделируемого показателя (Рис.3.1).

                                 Рис. 3.1 Таблица исходных данных

1.3.                    Сохранить таблицу данных в формате Microsoft Excel под своей фамилией в буфере. Для этого выполнить действия: отметить сохраняемый файл – меню «ФАЙЛ» - «СОХРАНИТЬ» (засветиться содержимое папки «Мои документы») – набрать имя сохраненного файла (своей фамилии) – «СОХРАНИТЬ».

1.4.                    Свернуть окно Excel . Перенести файл исходных данных в среду Microsoft Word-2000 и сохранить (для создания будущего отчета по лабораторной работе).

2.     Инсталяция программы «СтатЭксперт»

2.1.                    Выполнить последовательно действия: «ПУСК» - «ПРОГРАММЫ» (в главном меню) – «Olymp» - «СтатЭксперт» - «Не отключать макросы». На экране появиться картинка «СтатЭксперт».

2.2.                    Дать команду «Начало работы» - «OK». Появиться таблица программы «СтатЭксперт».

3.     Включить режимы обработки программы

3.1.                    Активизировать файл исходных данных, выполнив последовательно действия: «ФАЙЛ» - выбор имени файла из всплывающего меню в формате Excel.

3.2.                    Отметить цифровые данные таблицы.

3.3.                    Вызвать меню «СтатЭкс» (вторая строка панели инструментов), указать «ВРЕМЕННЫЕ РЯДЫ» (появиться окно «Установка блока данных») (Рис. 3.2).

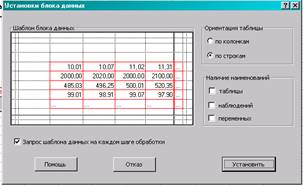
Рис. 3.2 Окно «Установки блока данных»

4.     Предварительная обработка данных

4.1.                    Ориентация таблицы: флажок в окно «по строкам», либо «по колонкам» (в зависимости от ориентации шаблона).

4.2.                    Наличие наименований: убрать все флажки в окнах.

4.3.                    Команда «Установить» (появиться окно «Обработка временных рядов»).

Окно «Обработка временных рядов» (Рис. 3.3).

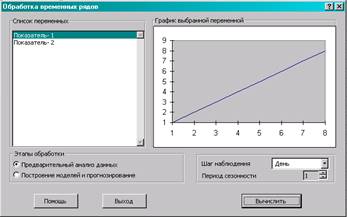
Рис. 3.3 Окно «Обработка временных рядов»

4.4.                    Этапы обработки: флажок в окно «Предварительный анализ».

4.5.                    Выделяем щелчком левой кнопки мышки «Показатель 2».

4.6.                    Команда «Вычислить» (появиться окно «Предварительный анализ данных»). Работа в окне «Предварительный анализ данных» (Рис.3.4).

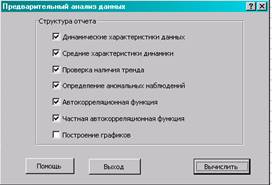
Рис. 3.4 Окно «Предварительный анализ данных»

4.7.                    Оставить все флажки, кроме «Построение графиков».

4.8.                    Команда «Вычислить».

4.9.                    При обнаружении аномальных данных в моделируемом временном ряду нажать клавишу «Да» и выполнить рекомендации всплывающего сообщения.

5.     Полученный протокол отчета (Рис.3.5)

Cтатистики временного ряда - Показатель-A
Базисные характеристики
Наблюдение	Абс. прирост	Темп роста	Темп прироста
2	1	200	100
3	2	300	200
4	3	400	300
5	4	500	400
6	5	600	500
7	6	700	600
8	7	800	700
9	8	900	800
10	9	1000	900
11	10	1100	1000
12	11	1200	1100
13	12	1300	1200
14	13	1400	1300
15	14	1500	1400
16	15	1600	1500
Цепные характеристики
Наблюдение	Абс. прирост	Темп роста	Темп прироста
2	1	200	100
3	1	150	50
4	1	133,333	33,333
5	1	125	25
6	1	120	20
7	1	116,667	16,667
8	1	114,286	14,286
9	1	112,5	12,5
10	1	111,111	11,111
11	1	110	10
12	1	109,091	9,091
13	1	108,333	8,333
14	1	107,692	7,692
15	1	107,143	7,143
16	1	106,667	6,667
Средние характеристики
Характеристика	Значение
Среднее арифметическое	8,5
Средний темп роста (%)	120,303
Средний темп прироста (%)	20,303
Средний абсолютный прирост	1
Гипотеза об отсутствии тренда
Метод проверки	Результат
Метод Форстера-Стюарта	Нет
Метод сравнения средних	Нет
Вывод: гипотеза отвергается
Проверка однородности данных
Аномальные наблюдения не обнаружены
Автокорреляционная функция
Лаг	Исходный ряд	Разностный ряд (d=1)
1	0,813	0,8
2	0,628	0,604
3	0,449	0,414
4	0,279	0,236
Cтандартные отклонения = +0.4788, +0.4652
Частная автокорреляционная функция
Лаг	Исходный ряд	Разностный ряд (d=1)
1	0,871	0,86
2	-0,01	-0,012
3	-0,011	-0,012
4	-0,097	-0,103
Cтандартные отклонения = +0.2500, +0.2673

Рис. 3.5 Отчет по предварительной обработке данных 1

6.     Построение модели и прогнозирование

6.1.                    Включить режимы обработки программы: активизировать файл исходных данных (шаблон) в формате Excel, отметить цифровые данные таблицы.

6.2.                    Вызвать меню «СтатЭкс» (верхняя строчка), указать «ВРЕНМЕННЫЕ РЯДЫ» (появиться окно «Установка блока данных»).

6.3.                    Предварительная обработка данных: ориентация таблицы (в зависимости от ориентации шаблона), наличие наименований (убрать все флажки в окнах); команда «Установить» (появиться окно «Обработка временных рядов») (Рис. 3.6).

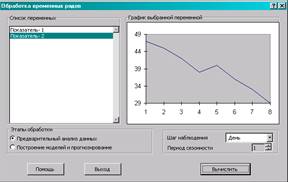
Рис. 3.6 Окно «Обработка временных рядов».

6.4.                    Этапы обработки: флажок в окно «Построение моделей и прогнозирование»; выделяем щелчком левой кнопки мышки «Показатель 2»; команда «Вычислить» (появиться окно «Построение моделей и прогнозирование») (Рис. 3.7).

Рис. 3.7 Окно «Построение моделей и прогнозирование»

6.5.                    Класс моделей: «Кривые роста».

6.6.                    Тип прогноза: «Прогноз вперед».

6.7.                    Способ построения прогноза: «На основе одной лучшей модели».

6.8.      Структура отчета: все флажки кроме «Статистика ретропрогноза».

6.9.      Период прогноза: в соответствии с условием задачи.

6.10. Вероятность свершения прогноза: в соответствии с условием задачи.

6.11. «Вычислить».

7.     Формирование отчета по графикам (Рис. 3.8)

Рис. 3.8 Окно «Графики отчета»

Модели временного ряда -  Показатель-B
Таблица кривых роста
Функция	Критерий	Эластич ность
Y(t)=+46.600+0.885*t	127,948	0,139
Y(t)=+45.296+1.320*t -0.026*t*t	137,503	0,138
Y(t)= +46.284*exp(+0.016*t)	129,298	0,135
Y(t)= +43.793+5.390*ln(t)	127,600	0,097
Y(t)= (+44.910)*(+1.026)**t*(+0.999)**(t*t)	138,782	0,000
Y(t)= +41.031-0.006*t+4.731*sqr(t)	137,229	0,125
Y(t)= t/(+0.013+0.017*t)	142,344	0,084
Выбрана функция Y(t)= +43.793+5.390*ln(t)
Характеристики базы моделей
Модель	Адекват ность	Точность	Качество
Y(t)= +43.793+5.390*ln(t)	78,106	2,251	21,215
Лучшая модель Y(t)= +43.793+5.390*ln(t)
Параметры моделей
Модель	a1	a2
Y(t)= +43.793+5.390*ln(t)	43,793	5,390
Таблица остатков
номер	Факт	Расчет	Ошибка абс.	Ошибка относит.
1	41,000	43,793	-2,793	-6,813
2	52,000	47,529	4,471	8,598
3	62,000	49,714	12,286	19,816
4	40,000	51,265	-11,265	-28,162
5	44,000	52,467	-8,467	-19,244
6	56,000	53,450	2,550	4,553
7	68,000	54,281	13,719	20,175
8	41,000	55,001	-14,001	-34,148
9	47,000	55,635	-8,635	-18,373
10	60,000	56,203	3,797	6,328
11	71,000	56,717	14,283	20,117
12	44,000	57,186	-13,186	-29,968
13	52,000	57,617	-5,617	-10,802
14	64,000	58,017	5,983	9,349
15	77,000	58,388	18,612	24,171
16	47,000	58,736	-11,736	-24,971
Характеристики остатков
Характеристика	Значение
Среднее значение	0,000
Дисперсия	111,650
Приведенная дисперсия	127,600
Средний модуль остатков	9,463
Относительная ошибка	17,849
Критерий Дарбина-Уотсона	2,245
Коэффициент детерминации	0,963
F - значение ( n1 =   1, n2 =  14)	369,465
Критерий адекватности	78,106
Критерий точности	2,251
Критерий качества	21,215
Уравнение значимо с вероятностью 0.95
Таблица прогнозов (p = 80%)
Упреждение	Прогноз	Нижняя граница	Верхняя граница
1	59,063	53,119	65,008
2	59,371	53,205	65,537
3	59,663	53,283	66,043

Рис. 3.9 Отчет по предварительной обработке данных 2

7.1.                    В активном окне протокола  «Стат Эксперт» нажать ярлык диаграммы (слева от окна, второй ярлык сверху). В появившимся меню выбрать «Аппроксимация и прогноз» (Рис. 3.8) (появиться график – Рис. 3.10).

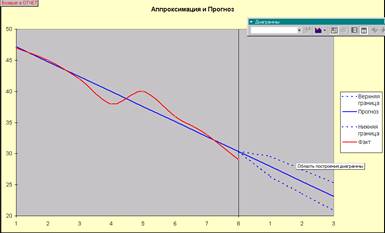
Рис.3.10 График аппроксимация и прогноз