Министерство
образования РФ
Всероссийский заочный
финансово-экономический институт
Кафедра статистики
КУРСОВАЯ РАБОТА
по дисциплине «Статистика»
на тему:
«Динамика результатов
производственной деятельности фирмы (организации), её статистическое изучение и
прогнозирование»
Исполнитель:
Клюева А.Ю.
Специальность:
менеджмент организации
Группа: день (город)
№ зачётной книжки: 05ММД10808
Руководитель: доцент Юдин А.А.
Владимир-2008
Содержание
Введение........................................................................................................ 3
Глава I. Теоретическая часть....................................................................... 4
1.1. Результаты производственной
деятельности фирмы.................... 4
1.2. Динамика производственной
деятельности фирмы...................... 7
1.3. Методы анализа и прогнозирования
результатов производственной деятельности.......................................................................................... 14
1.3.1. Анализ рядов динамики
результатов производственной
деятельности..........................................................................................
14
1.3.2. Методы прогнозирования
результатов производственной деятельности....................................................................................................................... 18
Глава II. Расчётная часть.............................................................................. 20
Глава III. Аналитическая часть.................................................................... 43
Заключение................................................................................................... 49
Список использованной литературы........................................................... 50
Введение
Статистика – это наука,
изучающая количественную сторону массовых общественных явлений в неразрывной
связи с качественной стороной. Основой существования общества является
экономическая деятельность, направленная на создание материальных благ и услуг,
предназначенных для удовлетворения личных и коллективных потребностей. Анализ
экономического развития страны предполагает
изучение процесса функционирования производства и оценку его
результатов.
Таким образом, именно статистическое изучение финансово –
экономической деятельности предприятий в
настоящее время приобретает
первостепенное значение для экономики страны.
В статистику производственной деятельности входит система
показателей, характеризующих объем производства, его структуру и динамику,
изучение основных закономерностей производства и определяющих его факторов. Прежде всего, в производственной деятельности ориентируются
на объем продаж и получение прибыли.
Процесс
развития, движения результатов производственной деятельности во времени в
статистике принято называть динамикой. Именно это явление - главная тема данной курсовой работы, в
которой будут рассмотрены виды результатов производственной деятельности,
способы статистического изучения их развития во времени и методы составления
прогнозов.
Глава I. Теоретическая часть
1.1
Результаты производственной
деятельности
Основой существования
общества является экономическая деятельность, направленная на создание
материальных благ и услуг, предназначенных для удовлетворения личных и
коллективных потребностей. Анализ экономического развития страны предполагает
изучение процесса функционирования производства и оценку его результатов.
Прямой полезный результат
производственной деятельности предприятий выражается в форме товаров и
материальных услуг. Объем продукции по промышленности в целом определяется как
сумма данных об объеме произведенной промышленной продукции, выполненных услуг
промышленного характера по всем юридическим
лицам вне зависимости от того, является ли промышленное производство их
основным видом деятельности. Но для оценки производства невозможно ограничится
лишь сведениями о количестве произведенной продукции одного вида в физических единицах
измерения, общий объем производства разнородной продукции по предприятию
(отрасли, региону, промышленности и экономике в целом) может быть определен
только в стоимостном выражении. Натуральные показатели продукции служат основой
стоимостного учета.
В теории и практике статистики известны
различные стоимостные показатели результатов производственной деятельности:
валовой оборот, валовая продукция, реализованная продукция, чистая продукция и
др.
Валовой оборот – характеризует общий объем
продукции, произведенный за какой-либо промежуток времени всеми
промышленно-производственными цехами предприятия не зависимо от того,
потреблена ли продукция в этом же периоде в других цехах предприятия, оставлена
ли она для использования в следующем периоде или отпущена на сторону. Валовой
объем определяется как сумма следующих элементов:
- стоимости готовых изделий, выработанных в отчетном периоде всеми
цехами предприятия;
- стоимости работ промышленного характера, выполненных по заказам со
стороны или для непромышленных подразделений своего предприятия;
- стоимости работ по модернизации или реконструкции собственного
оборудования и транспортных средств и др.
Валовая продукция (ВП) – характеризует конечный
результат промышленно-производственной деятельности предприятия за определенный
период времени. ВП представляет собой стоимости продукции всех
промышленно-производственных цехов за вычетом той ее части, которая была
использована внутри данного предприятия на собственные
промышленно-производственные нужды.
В состав ВП за отчетный период
включаются следующие элементы:
- состав готовых изделий, выработанных за отчетный период как из своего
сырья и материалов, так и из сырья заказчиков;
- стоимость остатков полуфабрикатов, инструментов и приспособлений своей
выработки, отпущенных в отчетном периоде на сторону;
- изменение остатков полуфабрикатов, инструментов и приспособлений
своего производства;
- стоимость работ промышленного характера, выполненных по заказам со
стороны;
- стоимость работ по модернизации или реконструкции собственного
оборудования и транспортных средств.
ВП характеризует полную стоимость произведенной
продукции, которая включает не только стоимость, вновь созданную на данном
предприятии в текущем периоде, но и стоимость, созданную на других предприятиях и перенесенную на продукт
в данном периоде. Именно этот показатель по своему содержанию ближе всего к
показателю « промышленный выпуск », принятому в системе национальных счетов.
Под реализованной
продукцией (РП) понимается
продукция, оплаченная покупателем в отчетном периоде, не зависимо от того,
когда она была произведена. В нее может
включаться часть стоимости товарной продукции[1]
предшествующего периода, оплата которой произведена в текущем периоде.
Чистая продукция (ЧП) представляет собой вновь созданную стоимость в текущем периоде. Ее
определяют как разность между ВП и стоимостью материальных производственных
затрат (сырья, материалов, топлива, энергии, услуг производственного характера,
износа основных производственных фондов).
Но в настоящее время эти
стоимостные показатели результатов производственной деятельности в рамках
предприятий и организаций не исчисляются.
В
статистику производства товаров и услуг входит система показателей, характеризующих объем производства,
его структура и динамика, изучение основных закономерностей производства и
определяющих его факторов.
Статистическое
изучение эффективности производства связано с использованием системы
показателей, исчисляемых как соотношение результатов и факторов производства
(ресурсов) или результатов и затрат, связанных с этим процессом. Экономическая
эффективность представляет собой сложную экономическую категорию, поэтому в
настоящее время в статистике для характеристики уровня и динамики экономической
эффективности применяется большое количество показателей, которое можно
объединить в следующие группы:
·
показатели
рентабельности производства;
·
показатели
эффективности затрат живого труда;
·
показатели
эффективности затрат овеществленного труда;
·
показатели
эффективности капиталовложений.
1.2 Динамика результатов производственной деятельности
Процесс развития и движения результатов
производственной деятельности во времени в статистике принято называть
динамикой. Ее статистическое изучение производится при помощи анализа рядов
динамики (или временных рядов).
Ряды
динамики представляют собой ряды
изменяющихся во времени значений статистического показателя, расположенных в
хронологическом порядке. В каждом ряду динамики имеются два основных элемента:
показатели времени t (годы, кварталы, месяцы, сутки) и
конкретное числовое значение показателя (уровень ряда) y.
Виды
рядов динамики могут классифицироваться по следующим признакам:
1.
в
зависимости от способа выражения уровней ряды динамики подразделяются на ряды
абсолютных, относительных и средних величин;
2.
в
зависимости от того выражают ли уровни ряда величину явления за определенные
моменты времени или его величину за определенные интервалы времени, различают
соответственно моментные и интервальные ряды динамики;
3.
в
зависимости от расстояния между уровнями ряды подразделяются на ряды с
равностоящими и неравностоящими уровнями по времени.
Построение
и анализ рядов динамики позволяют выявить и измерить закономерности развития
результатов производственной деятельности во времени. Эти закономерности не
проявляются четко на каждом конкретном уровне, а лишь в тенденции, в достаточно
длительной динамике. Но на основную закономерность динамики накладываются
другие, прежде всего случайные, иногда сезонные влияния. Выявление основной
тенденции в изменении уровней, именуемой трендом, и является одной из главных
задач анализа рядов динамики.
Анализ
скорости и интенсивности развития явления во времени осуществляется с помощью
статистических показателей, которые получаются в результате сравнения уровней
между собой. К таким показателям относятся: абсолютный прирост; темп роста и
прироста; абсолютное значение одного процента прироста.
При этом
принято сравниваемый уровень называть отчетным, а уровень, с которым происходит сравнение, - базисным.
Важнейшим статистическим показателем
анализа динамики является абсолютный прирост (сокращение) Δx, т.е. абсолютное изменение,
характеризующее увеличение или уменьшение уровня ряда за определенный
промежуток времени. Он равен разнице двух сравниваемых уровней и выражает
абсолютную скорость роста.
Абсолютные
приросты могут быть цепными (по отношению к предыдущему периоду) и базисными
(по отношению к какому-либо базисному периоду).
Абсолютный прирост:
Абсолютный прирост:
(цепной):
(базисный)
 ;
; 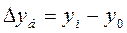
где 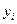 – уровень сравниваемого периода;
– уровень сравниваемого периода;
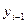 – уровень
предшествующего периода;
– уровень
предшествующего периода;
 – уровень
базисного периода.
– уровень
базисного периода.
Цепные и
базисные приросты связаны между собой: сумма последовательных цепных абсолютных
приростов равны базисному, т.е. общему приросту за весь промежуток времени:
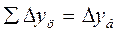
Для оценки интенсивности, т.е. относительного уровня
динамического ряда за какой-либо период времени исчисляются темпы роста
(снижения). Интенсивность изменения уровня оцениваются отношением отчетного
уровня к базисному.
Показатель
интенсивности изменения уровня ряда, выраженный в долях единицы, называется
коэффициентом роста, а в процентах
темпом роста.
Коэффициент роста (снижения) показывает, во сколько раз
сравниваемый уровень больше базисного (если этот коэффициент больше 1) или
какую часть базисного уровня составляет уровень текущего периода за некоторый
промежуток времени (если коэффициент меньше 1). Темп роста всегда представляет
собой положительное число.
Коэффициент роста
Коэффициент роста
(цепной):
(базисный)

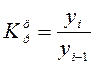
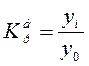
Темп роста
Темп роста
(цепной)
(базисный)
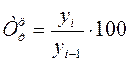
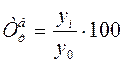
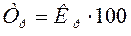
Относительную
оценку скорости изменения уровня ряда за единицу времени дают показатели темпа
прироста (сокращения).
Темп
прироста (сокращения) показывает, на сколько процентов сравниваемый уровень
больше или меньше базисного, и исчисляется как отношение абсолютного прироста к
абсолютному уровню, принятому за базу сравнения. Темп прироста может быть
положительным, отрицательным или равным нулю, выражается он в процентах или долях единицы (коэффициент прироста).
Темп прироста
Темп прироста
(цепной): (базисный):
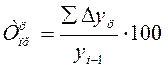
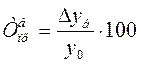
Темп прироста (сокращения) можно получить и из темпа роста,
выраженного в процентах, если из него вычесть 100%.
Коэффициент прироста получается вычитанием единицы из
коэффициента прироста:
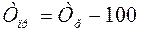 ;
; 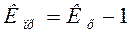
При анализе динамики результатов производственной деятельности
следует также знать, какие абсолютные значения скрываются за темпами роста и
прироста. Сравнение абсолютного прироста и темпа прироста за одни и те же
периоды времени показывает, что при снижении (замедлении) темпов прироста
абсолютный прирост не всегда уменьшается, в отдельных случаях он может
возрастать. Поэтому, чтобы правильно оценить значение полученного темпа
прироста, его рассматривают в сопоставлении с показателем абсолютного прироста.
Результат выражают показателем, который называется абсолютным значением
(содержанием )одного процента прироста и рассчитывают как отношение абсолютного
прироста к темпу прироста за
определенный период времени, %:
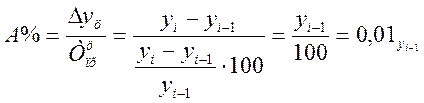
Абсолютное значение одного процента прироста равняется сотой
части предыдущего или базисного уровня. Оно показывает, какое абсолютное
значение скрывается за относительным показателем одного процента прироста.
В тех случаях, когда сравнение необходимо произвести с
отдалением периода времени, принятого за базу сравнения, рассчитывают так
называемые пункты роста, которые представляют собой разность базисных темпов
роста, %, двух смежных периодов.
В отличие от темпов роста, которые нельзя ни суммировать, ни
перемножать, пункты роста можно суммировать, в результате получится темп
прироста соответствующего периода по сравнению с базисным.
Для обобщающей характеристики
динамики результатов производственной деятельности определяют средние
показатели изменения уровней ряда.
Обобщающий показатель скорости изменения уровней во времени –
средний абсолютный прирост (убыль), представляющий собой обобщенную
характеристику индивидуальных абсолютных приростов ряда динамики. Этот показатель дает возможность установить,
насколько за единицу времени в среднем должен увеличиваться уровень ряда (в
абсолютном выражении), чтобы, отправляясь от начального уровня за данное число
периодов (например, лет) достигнуть конечного уровня.
По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний абсолютный прирост как
среднюю арифметическую простую:
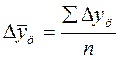 ,
,
где n- число цепных абсолютных приростов (Δyц) в изучаемом периоде.
Также средний абсолютный прирост можно определить через
накопленный (базисный) прирост (Δyб). Для случая
равных интервалов применяется следующая формула:
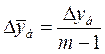 ,
,
где m- число уровней ряда динамики в изучаемом периоде, включая
базисный.
Сводной обобщающей характеристикой интенсивности изменения
уровней ряда динамики служит средний темп роста (снижения), показывающий, во
сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
Средний темп роста (снижения) – обобщенная характеристика
индивидуальных темпов роста ряда динамики. В качестве основы и критерия
правильности исчисления среднего темпа роста (снижения) применяется
определяющий показатель – произведение цепных темпов роста, равное темпу роста
за весь рассматриваемый период. Следовательно, если значение признака
образуется как произведение отдельных вариантов, то необходимо применить
среднюю геометрическую. Средний темп роста представляет собой средний
коэффициент роста, выраженный в процентах (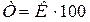 ). Для
равностоящих рядов динамики результатов производственной деятельности расчеты
по средней геометрической сводятся к исчислению средних коэффициентов роста из
цепных коэффициентов роста:
). Для
равностоящих рядов динамики результатов производственной деятельности расчеты
по средней геометрической сводятся к исчислению средних коэффициентов роста из
цепных коэффициентов роста:


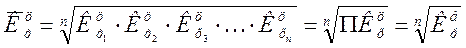 ,
,
где n-число цепных коэффициентов
роста;
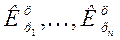 - цепные
коэффициенты роста;
- цепные
коэффициенты роста;
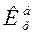 – базисный коэффициент
роста за весь период.
– базисный коэффициент
роста за весь период.
Если же известны уровни динамического ряда, то расчет
среднего коэффициента роста значительно упрощается. Т.к. произведение цепных
темпов роста равно базисному, то в подкоренное выражение подставляется базисный
коэффициент роста. Базисный коэффициент получается непосредственно как частное
от деления уровня последнего периода yn на уровень
базисного периода y0. тогда
формула для расчета среднего коэффициента роста для равностоящих рядов динамики
будет:
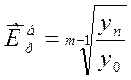 ,
,
где m- число уровней ряда динамики в изучаемом периоде, включая
базисный.
Средние темпы
прироста (сокращения) рассчитываются на основе средних темпов роста,
вычитанием из последних 100%. Соответственно при исчислении средних
коэффициентов прироста из значений коэффициентов роста вычитается единица:
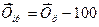 ;
; 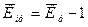
где 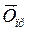 – средний темп прироста,
– средний темп прироста,
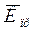 – средний коэффициент
прироста.
– средний коэффициент
прироста.
Если уровни ряда динамики снижаются, то средний темп роста
будет меньше ста процентов, а средний темп прироста – отрицательной величиной.
Положительный темп прироста 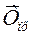 представляет собой
средний темп увеличения и характеризует среднюю относительную скорость увеличения
уровня.
представляет собой
средний темп увеличения и характеризует среднюю относительную скорость увеличения
уровня.
1.3. Методы анализа и прогнозирования динамики результатов производственной
деятельности
1.3.1. Анализ рядов динамики
результатов производственной деятельности
Одной из
важнейших задач статистики является определение в рядах динамики общей тенденции
развития явления (тренда). В некоторых случаях закономерность изменения
явления, общая тенденция его развития явно и отчетливо выражается уровнями
динамического ряда (уровни на изучаемом периоде непрерывно растут или
непрерывно снижаются).
Однако зачастую
встречаются такие ряды динамики, в которых уровни ряда претерпевают самые
различные изменения, возрастают, то убывают, и общая тенденция развития не
ясна. На развитие явления во времени оказывают влияние различные по характеру и
силе воздействия факторы. Одни из них воздействуют постоянно и формируют в
рядах динамики определенную тенденцию развития. воздействие же других факторов
может быть кратковременным или носить случайный характер.
Поэтому
при анализе динамики акцент делается на основную тенденцию, достаточно
стабильную и устойчивую на протяжении всего изучаемого этапа развития.
Основной
тенденцией развития (трендом) называется плавное и устойчивое изменение уровня
явления во времени, свободное тот случайных колебаний.
Главной
задачей является выявление общей тенденции в изменении уровней ряда,
освобожденных от действия различных
случайных факторов. С этой целью ряды динамики подвергаются обработке методами
укрупнения интервалов, скользящей средней и аналитического выравнивания.
Одним из
наиболее простых методов изучения основной тенденции в рядах динамики
результатов производственной деятельности является укрупнение интервалов. Он основан на укрупнении периодов времени, к
которым относятся уровни ряда динамики (одновременно уменьшается количество
интервалов). Например, ряд ежесуточного выпуска продукции заменяется рядом
месячного выпуска продукции и т.д.
Средняя,
исчисляемая по укрупненным интервалам, позволяет выявить направление и характер
(ускорение или замедление роста) основной тенденции развития, т.к. после
укрупнения интервалов основная тенденция развития производства становится
очевидной.
Выявление
основной тенденции может осуществятся также методом скользящей (подвижной)
средней. Суть его заключается в том, что исчисляется средний уровень из
определенного числа, обычно нечетного (3,5,7 и т.д.), первых по счету уровней
ряда, затем из такого же числа уровней, но начиная со второго по счету, далее –
начиная с третьего и т.д. таким образом, средняя как бы «скользит» по ряду
динамики, передвигаясь на один срок. Полученный сглаженный ряд короче
фактического. Он меньше подвержен
колебаниям из-за случайных причин, и четче выражает основную тенденцию развития
результатов производственной деятельности за изучаемый период.
Недостатком
сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с
фактическим, а следовательно, потеря информации.
Рассмотренные
приемы сглаживания динамических рядов (укрупнение интервалов и метод скользящей
средней) дают возможность определить лишь общую тенденцию развития явления,
более или менее от случайных и сезонных колебаний. Однако получить обобщенную
статистическую модель тренда посредством этих методов нельзя.
Для того
чтобы дать количественную модель, выражающую основную тенденции. Изменения
уровней динамического ряда во времени, используется аналитическое выравнивание
ряда динамики.
Основным
содержанием метода аналитического выравнивания в рядах динамики является то,
что общая тенденция развития рассчитывается как функция времени:
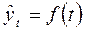 , где
, где 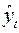 – уровни динамического ряда, вычисленные по
соответствующему аналитическому
уравнению на момент времени t.
– уровни динамического ряда, вычисленные по
соответствующему аналитическому
уравнению на момент времени t.
Определение
теоретических (расчетных) уровней 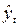 производится на
основе так называемой адекватной
математической модели, которая наилучшим образом отражает (аппроксимирует)
основную тенденцию ряда динамики.
производится на
основе так называемой адекватной
математической модели, которая наилучшим образом отражает (аппроксимирует)
основную тенденцию ряда динамики.
Простейшими
моделями (формулами), выражающими тенденцию развития, являются:
линейная
функция – прямая 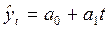 ,
,
где a0 , a1 – параметры уравнения; t – время;
показательная
функция 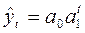 ;
;
степенная
функция – кривая второго порядка (парабола)
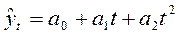 .
.
В тех случаях, когда требуется особо
точное изучение тенденции развития (например, модели тренда для
прогнозирования), при выборе вида адекватной функции можно использовало
специальные критерии математической статистики.
Расчет
параметров функции обычно производится при помощи метода наименьших квадратов, в
котором в качестве решения принимается точка минимума суммы квадратов отношений
между теоретическими и эмпирическими уровнями:
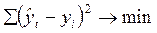 ,
,
где ŷt – выровненные (расчетные) уровни; yi – фактические уровни.
Параметры
уравнения ai , удовлетворяющие этому условию, могут быть найдены решением системы
нормальных уравнений. На основе найденного уравнения тренда вычисляются
варавненные уровни. Таким образом, выравнивание ряда динамики заключается в
замене фактических уровней yi плавно изменяющимися уровнями ŷt, наилучшим образом аппроксимирующими
статистические данные.
Выравнивание по прямой используется, как правило, в тех
случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни
изменяются в арифметической прогрессии (или близко к ней).
Выравнивание
по показательной функции используется в тех случаях, когда ряд отражает
развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста
практически постоянны.
1.3.2. Методы прогнозирования
результатов производственной деятельности.
Необходимым условием регулирования рыночных отношений
является составление надежных прогнозов развития
социально-экономических явлений.
Выявление и характеристика трендов и моделей взаимосвязи
создают основу для прогнозирования, т.е. для определения ориентировочных
размеров явления в будущем. Для этого используется метод экстраполяции.
Под экстраполяцией понимается нахождение уровней за пределами
изучаемого ряда, т.е. продление в будущее тенденции, наблюдавшейся в прошлом
(перспективная экстраполяция).
Но поскольку в действительности тенденция развития не
остается неизменной, то данные, получаемые путем экстраполяции ряда, надо
рассматривать как вероятностные оценки.
Экстраполяцию рядов динамки результатов производственной
деятельности осуществляют различными способами, например, экстраполируют ряды
динамики выравниванием по аналитическим формулам. Зная, уравнение для
теоретических уровней и подставляя в него значение t за пределами исследованного ряда, рассчитывают для t вероятностные
ŷt .
На практике результат экстраполяции прогнозируемых явлений
обычно получают не точечными (дискретными), интервальными оценками.
Для определения границ
интервалов используют формулу:
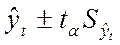 ,
,
Где tα –
коэффициент доверия по распределению Стьюдента;
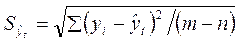
 – остаточное
среднее отклонение от тренда,
– остаточное
среднее отклонение от тренда,
скорректированное по числу степеней свободы
(n - m);
n – число уровней ряда динамики;
m – число параметров
адекватной модели тренда (для уравнения прямой m=2).
Вероятностные границы интервала
прогнозируемого явления:
 .
.
Экстраполяция в рядах динамики носит не только приближенный, но и условный
характер. Поэтому ее надо рассматривать как предварительный этап в разработке прогнозов.
Для составления прогноза должна быть привлечена дополнительная информация, не
содержащаяся в самом динамическом ряду.
Глава II. Расчётная часть.
Задание 1
1) Постройте статистический ряд распределения организаций по
признаку уровень среднегодовой заработной платы, образовав 5 групп с равными
интервалами.
2) Постройте графики полученного ряда распределения.
3) Рассчитайте характеристики ряда распределения: среднюю
арифметическую, среднее квадратическое отклонение, коэффициент вариации.
4) Вычислите среднюю арифметическую по исходным данным (таб. 2)
Задание 2
1)
Установите
наличие и характер связи между признаками фондовооруженность труда, и
среднегодовая заработная плата, образовав 5 групп с равными интервалами по
обоим признакам, методом аналитической группировки.
2)
Измерьте тесноту корреляционной связи между названными
признаками с использованием коэффициента детерминации и эмпирического
корреляционного отношения. Сделайте выводы.
Задание 3
По результатам
выполнения задания 1 с вероятностью 0,954 определите:
1.
Ошибку выборки среднего уровня заработной платы и
границы, в которых будет находиться средняя заработная плата в генеральной
совокупности.
2. Ошибку выборки доли организации с уровнем среднегодовой
заработной платы 86,4 тыс. руб. и более и границы, в которых будет находиться
генеральная доля.
Задание 4
Имеются следующие данные по организации о динамик выпуска
продукции:
|
Годы
|
Выпуск продукции в
сопоставимых ценах, млн. руб.
|
По сравнению с предыдущим
годом
|
|
Абсолютный прирост, млн.
руб.
|
Темп роста, %
|
Темп прироста, %
|
Абмолютнон содержание 1 %
прироста, млн.руб.
|
|
1998
|
|
|
|
|
|
|
1999
|
|
|
98
|
|
|
|
2000
|
|
|
|
1
|
0.18
|
|
2001
|
|
4
|
|
|
|
|
2002
|
|
|
100
|
|
|
Определить все недостающие показатели ряда динамики и
занесите их в таблицу. Постройте графики. Осуществите прогноз выпуска продукции
на ближайшие два года с помощью среднего абсолютного прироста. Сделайте выводы.
Задание 1
|
|
|
|
|
Таблица 1.1
|
|
|
|
Таблица исходных данных
|
|
№ Организации
|
Среднесписочная
численность работников, чел.
|
Выпуск продукции,
млн. руб.
|
Фонд заработной
платы, млн. руб.
|
Затраты на
производство продукции, млн. руб.
|
|
1
|
162
|
36,45
|
11,34
|
30,255
|
|
2
|
156
|
23,4
|
8,112
|
20,124
|
|
3
|
179
|
46,54
|
15,036
|
38,163
|
|
4
|
194
|
59,752
|
19,012
|
47,204
|
|
5
|
165
|
41,415
|
13,035
|
33,546
|
|
6
|
158
|
26,86
|
8,535
|
22,831
|
|
7
|
220
|
79,2
|
26,4
|
60,984
|
|
8
|
190
|
54,72
|
17,1
|
43,776
|
|
9
|
163
|
40,424
|
12,062
|
33,148
|
|
10
|
159
|
30,21
|
9,54
|
25,376
|
|
11
|
167
|
42,418
|
13,694
|
34,359
|
|
12
|
205
|
64,575
|
21,32
|
51,014
|
|
13
|
187
|
51,612
|
16,082
|
41,806
|
|
14
|
161
|
35,42
|
10,465
|
29,753
|
|
15
|
120
|
14,4
|
4,32
|
12,528
|
|
16
|
162
|
36,936
|
11,502
|
31,026
|
|
17
|
188
|
53,392
|
16,356
|
42,714
|
|
18
|
164
|
41
|
12,792
|
33,62
|
|
19
|
192
|
55,68
|
17,472
|
43,987
|
|
20
|
130
|
18,2
|
5,85
|
15,652
|
|
21
|
159
|
31,8
|
9,858
|
26,394
|
|
22
|
162
|
39,204
|
11,826
|
32,539
|
|
23
|
193
|
57,128
|
18,142
|
45,702
|
|
24
|
158
|
28,44
|
8,848
|
23,89
|
|
25
|
168
|
43,344
|
13,944
|
35,542
|
|
26
|
208
|
70,72
|
23,92
|
54,454
|
|
27
|
166
|
41,832
|
13,28
|
34,302
|
|
28
|
207
|
69,345
|
22,356
|
54,089
|
|
29
|
161
|
35,903
|
10,948
|
30,159
|
|
30
|
186
|
50,22
|
15,81
|
40,678
|
1.
Чтобы образовать пять групп с равными
интервалами:
1)
Распределим полученные значения по возрастанию по
признаку Уровень среднегодовой заработной платы.
2)
Для более
удобного и наглядного вычисления представим данные уровня среднегодовой
заработной платы в рублях, а не в млн. руб.
|
|
|
|
Таблица 1.2
|
|
№ Организации
|
Среднесписочная
численность работников, чел.
|
Фонд заработной платы,
млн. руб.
|
Уровень
среднегодовой заработной платы, руб.
|
|
15
|
120
|
4,32
|
36000
|
|
20
|
130
|
5,85
|
45000
|
|
2
|
156
|
8,112
|
52000
|
|
6
|
158
|
8,532
|
54000
|
|
24
|
158
|
8,848
|
56000
|
|
10
|
159
|
9,54
|
60000
|
|
21
|
159
|
9,858
|
62000
|
|
14
|
161
|
10,465
|
65000
|
|
29
|
161
|
10,948
|
68000
|
|
1
|
162
|
11,34
|
70000
|
|
16
|
162
|
11,502
|
71000
|
|
22
|
162
|
11,826
|
73000
|
|
9
|
163
|
12,062
|
74000
|
|
18
|
164
|
12,792
|
78000
|
|
5
|
165
|
13,035
|
79000
|
|
27
|
166
|
13,28
|
80000
|
|
11
|
167
|
13,694
|
82000
|
|
25
|
168
|
13,944
|
83000
|
|
3
|
179
|
15,036
|
84000
|
|
30
|
186
|
15,81
|
85000
|
|
13
|
187
|
16,082
|
86000
|
|
17
|
188
|
16,356
|
87000
|
|
8
|
190
|
17,1
|
90000
|
|
19
|
192
|
17,472
|
91000
|
|
23
|
193
|
18,142
|
94000
|
|
4
|
194
|
19,012
|
98000
|
|
12
|
205
|
21,32
|
104000
|
|
28
|
207
|
22,356
|
108000
|
|
26
|
208
|
23,92
|
115000
|
|
7
|
220
|
26,4
|
120000
|
|
Итого
|
5190
|
418,954
|
2350000
|
|
Ср.арифметич
|
173
|
13,96513333
|
78333,33333
|
При
построении ряда с равными интервалами величина интервала h определяется по формуле
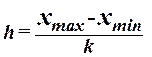 ,
,
где 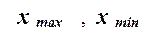 – наибольшее и наименьшее значения
признака в исследуемой совокупности, k- число групп
интервального ряда.
– наибольшее и наименьшее значения
признака в исследуемой совокупности, k- число групп
интервального ряда.
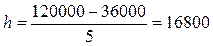 руб.
руб.
При h = 16800 руб. границы интервалов ряда
распределения имеют следующий вид (табл. 1.3):
|
|
|
Таблица 1.3
|
|
Номер группы
|
Нижняя граница,
руб.
|
Верхняя граница,
руб.
|
|
1
|
36000
|
52800
|
|
2
|
52800
|
69600
|
|
3
|
69600
|
86400
|
|
4
|
86400
|
103200
|
|
5
|
103200
|
120000
|
Определяем число предприятий, входящих в каждую группу,
используя принцип полуоткрытого интервала [ ), согласно которому
предприятия со значениями признаков, которые служат одновременно верхними и
нижними границами смежных интервалов (52800, 69600, 86400 и 103200 рублей),
будем относить ко второму из смежных интервалов.
Для определения числа предприятий в
каждой группе строим разработочную таблицу 1.4
|
|
|
|
Таблица 1.4
|
|
Разработочная
таблица для построения интервального ряда распределения и аналитической
группировки
|
|
Группы предприятий
по уровню среднегодовой заработной платы, руб.
|
Номер предприятия
|
Уровень
среднегодовой заработной платы, руб.
|
Фондовооружённость
труда, руб.
|
|
1
|
2
|
3
|
4
|
|
36000-52800
|
15
|
36000
|
133000
|
|
|
20
|
45000
|
149000
|
|
|
2
|
52000
|
156000
|
|
Всего
|
3
|
133000
|
438000
|
|
52800-69600
|
6
|
54000
|
173000
|
|
|
24
|
56000
|
182000
|
|
|
10
|
60000
|
190000
|
|
|
21
|
62000
|
196000
|
|
|
14
|
65000
|
213000
|
|
|
29
|
68000
|
214000
|
|
Всего
|
6
|
365000
|
1168000
|
|
69600-86400
|
1
|
70000
|
214000
|
|
|
16
|
71000
|
215000
|
|
|
22
|
73000
|
228000
|
|
|
9
|
74000
|
233000
|
|
|
18
|
78000
|
234000
|
|
|
5
|
79000
|
232000
|
|
|
27
|
80000
|
231000
|
|
|
11
|
82000
|
231000
|
|
|
25
|
83000
|
235000
|
|
|
3
|
84000
|
232000
|
|
|
30
|
85000
|
241000
|
|
|
13
|
86000
|
244000
|
|
Всего
|
12
|
945000
|
2770000
|
|
86400-103200
|
17
|
87000
|
247000
|
|
|
8
|
90000
|
248000
|
|
|
|
91000
|
248000
|
|
|
19
|
94000
|
251000
|
|
|
23
|
98000
|
259000
|
|
Всего
|
5
|
460000
|
1253000
|
|
103200-120000
|
12
|
104000
|
256000
|
|
|
28
|
108000
|
268000
|
|
|
26
|
115000
|
266000
|
|
|
7
|
120000
|
277000
|
|
Всего
|
4
|
447000
|
1067000
|
|
Итого
|
30
|
2350000
|
6696000
|
На основе групповых итоговых строк «Всего» табл. 1.4
формируем итоговую таблицу 1.5, представляющую интервальный ряд распределения
предприятий по уровню среднегодовой заработной платы.
|
|
|
Таблица 1.5
|
|
Номер группы
|
Группы по
уровню среднегодовой заработной платы, руб.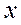
|
Число
предприятий,
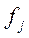
|
|
1
|
36000-52800
|
3
|
|
2
|
52800-69600
|
6
|
|
3
|
69600-86400
|
12
|
|
4
|
86400-103200
|
5
|
|
5
|
103200-120000
|
4
|
|
|
ИТОГО
|
30
|
Приведем еще три характеристики полученного ряда
распределения - частоты групп в
относительном выражении, накопленные (кумулятивные) частоты Sj, получаемые путем
последовательного суммирования частот всех предшествующих (j-1)
интервалов, и накопленные частости, рассчитываемые по формуле 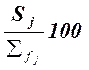 .
.
|
|
|
|
|
|
Таблица 1.6
|
|
Структура
предприятий по уровню среднегодовой заработной платы
|
|
Номер группы
|
 Группы
предприятий по уровню среднегодовой заработной платы, руб. Группы
предприятий по уровню среднегодовой заработной платы, руб.
|
 Число
предприятий, Число
предприятий,
|
 Накопленная
частота, Накопленная
частота,
|
Накопленная
частость, %
|
|
в абсолютном
выражении
|
в % к итогу
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
36000-52800
|
3
|
10
|
3
|
10
|
|
2
|
52800-69600
|
6
|
20
|
9
|
30
|
|
3
|
69600-86400
|
12
|
40
|
21
|
70
|
|
4
|
86400-103200
|
5
|
17
|
26
|
87
|
|
5
|
103200-120000
|
4
|
13
|
30
|
100
|
|
|
ИТОГО
|
30
|
100
|
|
|
Вывод. Анализ
интервального ряда распределения изучаемой совокупности предприятий показывает,
что предприятий по уровню среднегодовой заработной платы не является
равномерным: преобладают фирмы со среднегодовой заработной платой от 69600 руб.
до 86400 руб. (это 12 предприятий, доля которых составляет 40%); 30% предприятий
имеют среднегодовую заработную плату менее 69600 руб., а 30% - более 86400 руб.
2. Нахождение моды и медианы полученного интервального
ряда распределения графическим методом и путем расчетов
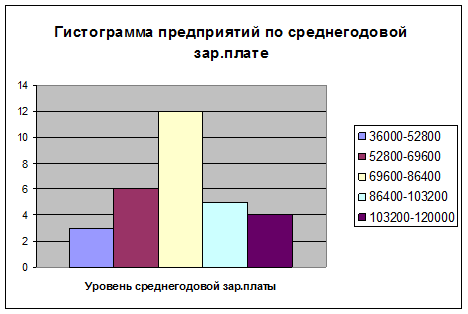
Для определения моды графическим методом строим
по данным табл. 1.5 (графы 2 и 3) гистограмму распределения предприятий по
изучаемому признаку.
Расчет конкретного
значения моды для интервального ряда распределения производится по формуле:
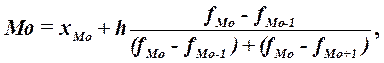
где хМo – нижняя
граница модального интервала,
h – величина модального интервала,
fMo – частота
модального интервала,
fMo-1 – частота
интервала, предшествующего модальному,
fMo+1 – частота
интервала, следующего за модальным.
Согласно
табл. 1.5 модальным интервалом построенного ряда является интервал 69600-86400
руб., т.к. он имеет наибольшую частоту (f3=12). Расчет моды:
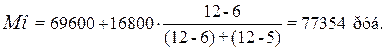
Вывод. Для
рассматриваемой совокупности предприятий наиболее распространенная
среднегодовая заработная плата характеризуется средней величиной 77354 рубля.
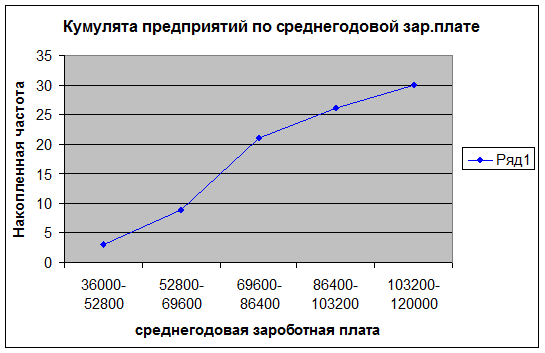
Для определения медианы графическим методом
строим по данным табл. 1.6 (графы 2 и 5) кумуляту распределения предприятий по
изучаемому признаку.
Расчет конкретного значения медианы для
интервального ряда распределения производится по формуле
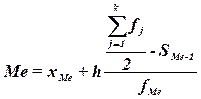 ,
,
где хМе– нижняя граница
медианного интервала,
h – величина медианного интервала,
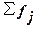 – сумма всех частот,
– сумма всех частот,
fМе – частота медианного
интервала,
SMе-1 – кумулятивная
(накопленная) частота интервала, предшествующего медианному.
Определяем
медианный интервал, используя графу 5 табл. 1.6. Медианным интервалом является
интервал 69600-86400 руб., т.к. именно в этом интервале накопленная частота Sj=21 впервые
превышает полусумму всех частот 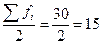 .
.
Расчет
медианы:
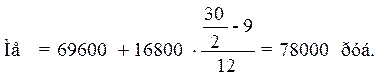
Вывод. В
рассматриваемой совокупности предприятий половина предприятий имеют
среднегодовую заработную плату не более 78000 рублей, а другая половина – не
менее 78000 рублей.
3. Расчет характеристик ряда
распределения
Для расчета характеристик ряда распределения 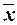 , σ, σ2, Vσ на основе табл. 1.6 строим
вспомогательную таблицу 1.7 (
, σ, σ2, Vσ на основе табл. 1.6 строим
вспомогательную таблицу 1.7 (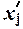 – середина интервала).
– середина интервала).
Таблица
1.7.Расчетная таблица для нахождения характеристик ряда распределения
|
Группы предприятий
по уровню среднегодовой заработной платы, руб.,
|
Середина интервала,
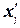
|
Число предприят.,
fj
|
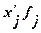
|
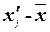
|
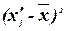
|
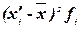
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
36000-52800
|
44400
|
3
|
133200
|
-33933,33
|
1151470885
|
34544112655
|
|
52800-69600
|
61200
|
6
|
367200
|
-17133,33
|
293550997
|
1761305981
|
|
69600-86400
|
78000
|
12
|
936000
|
-333,33
|
111108,889
|
1333306,667
|
|
86400-103200
|
94800
|
5
|
474000
|
16466,67
|
271151221
|
1355756104
|
|
103200-120000
|
111600
|
4
|
446400
|
33266,67
|
1106671333
|
4426685332
|
|
Итого
|
|
30
|
2356800
|
|
|
10999493379
|
Рассчитаем
среднюю арифметическую взвешенную:
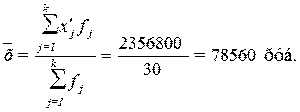
Рассчитаем среднее квадратическое
отклонение:
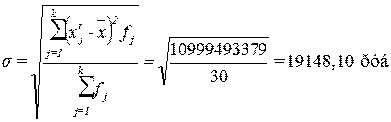
Рассчитаем дисперсию:
σ2 = 19148,102 = 36664977
Рассчитаем коэффициент вариации:
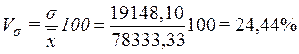
Вывод. Анализ
полученных значений показателей 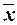 и σ говорит о том, что
средняя величина среднегодовой заработной платы составляет 78333,33 руб.,
отклонение от этой величины в ту или иную сторону составляет в среднем 19148,10
руб. (или 24,44%), наиболее характерная среднегодовая заработная плата
находится в пределах от 59185,22 до 97481,44
руб. (диапазон
и σ говорит о том, что
средняя величина среднегодовой заработной платы составляет 78333,33 руб.,
отклонение от этой величины в ту или иную сторону составляет в среднем 19148,10
руб. (или 24,44%), наиболее характерная среднегодовая заработная плата
находится в пределах от 59185,22 до 97481,44
руб. (диапазон 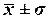 ).
).
Значение Vσ = 24,44% не превышает 33%,
следовательно, вариация среднегодовой заработной платы в исследуемой
совокупности предприятий незначительна и совокупность по данному признаку
однородна.
4. Вычисление средней арифметической по исходным
данным о среднегодовой заработной
плате предприятий
Для расчета применяется формула средней арифметической
простой:
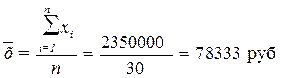 .
.
Причина
расхождения средних величин, рассчитанных по исходным данным (78333 руб.) и по
интервальному ряду распределения (78560 руб.), заключается в том, что в первом
случае средняя определяется по фактическим
значениям исследуемого признака для всех 30-ти фирм, а во втором случае в
качестве значений признака берутся середины
интервалов 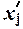 и,
следовательно, значение средней будет менее точным. Вместе с тем, при
округлении обеих рассматриваемых величин их значения совпадают (35 чел.), что
говорит о достаточно равномерном распределении численности менеджеров внутри
каждой группы интервального ряда.
и,
следовательно, значение средней будет менее точным. Вместе с тем, при
округлении обеих рассматриваемых величин их значения совпадают (35 чел.), что
говорит о достаточно равномерном распределении численности менеджеров внутри
каждой группы интервального ряда.
Задание 2
1. Целью выполнения данного задания является
выявление наличия корреляционной связи между факторным и результативным
признаками, а также установление направления связи и оценка ее тесноты.
По
условию Задания 2 факторным является признак фондовооруженность труда, результативным – признак среднегодовая заработная плата.
Метод аналитической группировки.
Аналитическая
группировка строится по факторному признаку Х и для каждой j-ой группы
ряда определяется среднегрупповое значение 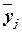 результативного признака Y. Если с
ростом значений фактора Х от группы
к группе средние значения
результативного признака Y. Если с
ростом значений фактора Х от группы
к группе средние значения 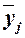 систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
систематически
возрастают (или убывают), между признаками X и Y имеет
место корреляционная связь.
При
построении ряда с равными интервалами величина интервала h определяется по формуле
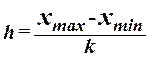 ,
,
где 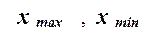 – наибольшее и наименьшее
значения признака в исследуемой совокупности, k- число
групп интервального ряда.
– наибольшее и наименьшее
значения признака в исследуемой совокупности, k- число
групп интервального ряда.
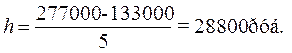
При h = 28800 руб. границы интервалов ряда
распределения имеют следующий вид (табл. 2.1):
Таблица 2.1
|
Номер группы
|
Нижняя граница,
руб.
|
Верхняя граница, руб.
|
|
1
|
133000
|
161800
|
|
2
|
161800
|
190600
|
|
3
|
190600
|
219400
|
|
4
|
219400
|
248200
|
|
5
|
248200
|
277000
|
Используя
разработочную таблицу 2.1, строим аналитическую группировку, характеризующую
зависимость между факторным признаком Х-
фондовооруженность труда и результативным
признаком Y – среднегодовая
заработная плата.
Для
определения числа предприятий в каждой группе строим разработочную таблицу 2.2.
Таблица 2.2
Разработочная таблица для
построения интервального ряда распределения и аналитической группировки
|
Группы предприятий
по уровню среднегодовой заработной платы, руб.
|
Номер
предприятия
|
Фондовооруженность
труда, руб.
|
Уровень
среднегодовой заработной платы, руб.
|
|
1
|
2
|
3
|
4
|
|
133000-161800
|
15
|
133000
|
36000
|
|
|
20
|
149000
|
45000
|
|
|
2
|
156000
|
52000
|
|
Всего
|
3
|
438000
|
133000
|
|
161800-190600
|
6
|
173000
|
54000
|
|
|
24
|
182000
|
56000
|
|
|
10
|
190000
|
60000
|
|
Всего
|
3
|
545000
|
170000
|
|
190600-219400
|
21
|
196000
|
62000
|
|
|
14
|
213000
|
65000
|
|
|
29
|
214000
|
68000
|
|
|
1
|
214000
|
70000
|
|
|
16
|
215000
|
71000
|
|
Всего
|
5
|
1052000
|
336000
|
|
219400-248200
|
22
|
228000
|
73000
|
|
|
9
|
233000
|
74000
|
|
|
18
|
234000
|
78000
|
|
|
5
|
232000
|
79000
|
|
|
27
|
231000
|
80000
|
|
|
11
|
231000
|
82000
|
|
|
25
|
235000
|
83000
|
|
|
3
|
232000
|
84000
|
|
|
30
|
241000
|
85000
|
|
|
13
|
244000
|
86000
|
|
|
17
|
247000
|
87000
|
|
|
8
|
248000
|
90000
|
|
|
19
|
248000
|
91000
|
|
Всего
|
13
|
3084000
|
1072000
|
|
248200-277000
|
23
|
251000
|
94000
|
|
|
4
|
259000
|
98000
|
|
|
12
|
256000
|
104000
|
|
|
28
|
268000
|
108000
|
|
|
26
|
266000
|
115000
|
|
|
7
|
277000
|
120000
|
|
Всего
|
6
|
1577000
|
639000
|
|
Итого
|
30
|
6696000
|
2350000
|
Построенную
аналитическую группировку представляет табл. 2.3:
Таблица 2.3
Зависимость среднегодовой заработной платы от
фондовооруженности труда
|
Номер группы
|
Фондовооруженность
труда, руб.,
x
|
Число предпр.,
fj
|
Среднегодовая
заработная плата, руб.
|
|
всего
|
в среднем на одну
фирму,
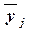
|
|
1
|
2
|
3
|
4
|
5=4:3
|
|
1
|
133000-161800
|
3
|
133000
|
44333,33
|
|
2
|
161800-190600
|
3
|
170000
|
56666,67
|
|
3
|
190600-219400
|
5
|
336000
|
67200
|
|
4
|
219400-248200
|
13
|
1072000
|
82461,54
|
|
5
|
248200-277000
|
6
|
639000
|
106500
|
|
|
ИТОГО
|
30
|
2350000
|
|
Вывод. Анализ
данных табл. 2.3 показывает, что с увеличением фондовооруженности труда от
группы к группе систематически возрастает и среднегодовая заработная плата
группе предприятий, что свидетельствует о наличии прямой корреляционной связи
между исследуемыми признаками.
Применение метода корреляционной таблицы.
Корреляционная таблица строится как комбинация двух рядов распределения
по факторному признаку Х и
результативному признаку Y. На пересечении j-ой строки и k-ой графы
таблицы указывается число единиц совокупности, входящих в j-ый интервал по признаку X и в k-ый интервал по признаку Y.
Концентрация частот около диагонали построенной таблицы свидетельствует о
наличии корреляционной связи между признаками - прямой или обратной. Связь
прямая, если частоты располагаются по диагонали, идущей от левого верхнего угла
к правому нижнему, обратная - по диагонали от правого верхнего угла к левому
нижнему.
Для построения корреляционной таблицы необходимо знать
величины и границы интервалов по двум признакам X и Y.
Используя группировки по факторному и результативному
признакам, строим корреляционную таблицу (табл. 2.4).
Таблица 2.4
Корреляционная таблица
зависимости среднегодовой заработной платы
от фондовооруженности труда
|
Группы
фирм по фондовооруженности труда, руб.
|
Группы
фирм по среднегодовой заработной плате, руб.
|
ИТОГО
|
|
36000-528000
|
52800-69600
|
69600-86400
|
86400-103200
|
103200-120000
|
|
|
|
133000-161800
|
3
|
|
|
|
|
3
|
|
|
161800-190600
|
|
3
|
|
|
|
3
|
|
|
190600-219400
|
|
3
|
2
|
|
|
5
|
|
|
219400-248200
|
|
|
10
|
3
|
|
13
|
|
|
248200-277000
|
|
|
|
2
|
4
|
6
|
|
|
ИТОГО
|
3
|
6
|
12
|
5
|
4
|
30
|
|
Вывод. Анализ
данных табл. 2.4 показывает, что распределение частот групп произошло вдоль
диагонали, идущей из левого верхнего угла в правый нижний угол таблицы. Это
свидетельствует о наличии прямой корреляционной связи между фондовооруженностью
труда и среднегодовой заработной платой.
2. Измерение тесноты
корреляционной связи с использованием коэффициента детерминации 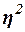 и эмпирического
корреляционного отношения
и эмпирического
корреляционного отношения 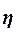
Коэффициент
детерминации 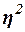 характеризует силу
влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля межгрупповой дисперсии
характеризует силу
влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля межгрупповой дисперсии 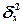 признака Y в его общей дисперсии
признака Y в его общей дисперсии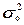 :
:
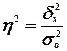
где 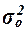 – общая дисперсия
признака Y,
– общая дисперсия
признака Y,
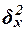 – межгрупповая
(факторная) дисперсия признака Y.
– межгрупповая
(факторная) дисперсия признака Y.
Общая дисперсия 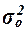 характеризует
вариацию результативного признака, сложившуюся под влиянием всех
действующих на Y факторов (систематических и случайных) и вычисляется по формуле
характеризует
вариацию результативного признака, сложившуюся под влиянием всех
действующих на Y факторов (систематических и случайных) и вычисляется по формуле
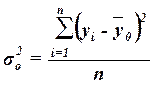
где yi
– индивидуальные значения результативного признака;
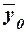 – общая средняя значений
результативного признака;
– общая средняя значений
результативного признака;
n – число единиц
совокупности.
Межгрупповая дисперсия 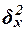 измеряет систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х
(по которому произведена группировка) и вычисляется по формуле
измеряет систематическую вариацию результативного признака,
обусловленную влиянием признака-фактора Х
(по которому произведена группировка) и вычисляется по формуле
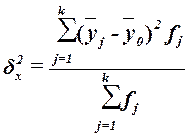
где 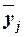 –групповые средние,
–групповые средние,
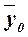 – общая средняя,
– общая средняя,
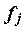 –число единиц в j-ой группе,
–число единиц в j-ой группе,
k – число
групп.
Для
расчета показателей 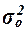 и
и 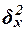 необходимо знать
величину
общей средней
необходимо знать
величину
общей средней 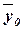 , которая вычисляется как средняя арифметическая простая
по всем единицам совокупности:
, которая вычисляется как средняя арифметическая простая
по всем единицам совокупности:
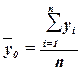
Значения
числителя и знаменателя формулы имеются в табл. 2.3 (графы 3 и 4 итоговой
строки). Используя эти данные, получаем общую среднюю 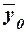 :
:
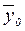 = 2350000/30=78333,33 руб.
= 2350000/30=78333,33 руб.
Для
расчета общей дисперсии 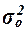 применяется
вспомогательная таблица 2.5:
применяется
вспомогательная таблица 2.5:
Таблица
2.5
Вспомогательная таблица для
расчета общей дисперсии
|
Номер
предприятия
|
Среднегодовая
заработная плата, руб.
|
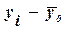
|
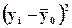
|
|
1
|
2
|
3
|
4
|
|
1
|
36000
|
-42 333,33
|
1 792 110 828,89
|
|
2
|
45000
|
-33 333,33
|
1 111 110 888,89
|
|
3
|
52000
|
-26 333,33
|
693 444 268,89
|
|
4
|
54000
|
-24 333,33
|
592 110 948,89
|
|
5
|
56000
|
-22 333,33
|
498 777 628,89
|
|
6
|
60000
|
-18 333,33
|
336 110 988,89
|
|
7
|
62000
|
-16 333,33
|
266 777 668,89
|
|
8
|
65000
|
-13 333,33
|
177 777 688,89
|
|
9
|
68000
|
-10 333,33
|
106 777 708,89
|
|
10
|
70000
|
-8 333,33
|
69 444 388,89
|
|
11
|
71000
|
-7 333,33
|
53 777 728,89
|
|
12
|
73000
|
-5 333,33
|
28 444 408,89
|
|
13
|
74000
|
-4 333,33
|
18 777 748,89
|
|
14
|
78000
|
-333,33
|
111 108,89
|
|
15
|
79000
|
666,67
|
444 448,89
|
|
16
|
80000
|
1 666,67
|
2 777 788,89
|
|
17
|
82000
|
3 666,67
|
13 444 468,89
|
|
18
|
83000
|
4 666,67
|
21 777 808,89
|
|
19
|
84000
|
5 666,67
|
32 111 148,89
|
|
20
|
85000
|
6 666,67
|
44 444 488,89
|
|
21
|
86000
|
7 666,67
|
58 777 828,89
|
|
22
|
87000
|
8 666,67
|
75 111 168,89
|
|
23
|
90000
|
11 666,67
|
136 111 188,89
|
|
24
|
91000
|
12 666,67
|
160 444 528,89
|
|
25
|
94000
|
15 666,67
|
245 444 548,89
|
|
26
|
98000
|
19 666,67
|
386 777 908,89
|
|
27
|
104000
|
25 666,67
|
658 777 948,89
|
|
28
|
108000
|
29 666,67
|
880 111 308,89
|
|
29
|
115000
|
36 666,67
|
1 344 444 688,89
|
|
30
|
120000
|
41 666,67
|
1 736 111 388,89
|
|
Итого
|
2350000
|
|
11 542 666 666,67
|
Рассчитаем общую дисперсию:
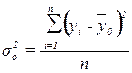 =11542666666,67/30=384755555,56
=11542666666,67/30=384755555,56
Для расчета межгрупповой дисперсии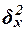 строится вспомогательная таблица 2.6. При этом
используются групповые средние значения
строится вспомогательная таблица 2.6. При этом
используются групповые средние значения 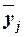 .
.
Таблица 2.6
Вспомогательная
таблица для расчета межгрупповой дисперсии
|
Фондовооруженность,
руб.,
x
|
Число
фирм,
fj
|
Среднее значение в
группе, руб.
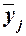
|
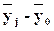
|
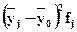
|
|
1
|
2
|
3
|
4
|
5
|
|
133000-161800
|
3
|
44333,33
|
-34000
|
3467999320
|
|
161800-190600
|
3
|
56666,67
|
-21666,7
|
1408332900
|
|
190600-219400
|
5
|
67200
|
-11133,3
|
619755184,4
|
|
219400-248200
|
13
|
82461,54
|
4128,208
|
221547366,3
|
|
248200-277000
|
6
|
106500
|
28166,67
|
4760167793
|
|
ИТОГО
|
30
|
|
|
10477802564
|
Рассчитаем межгрупповую дисперсию:
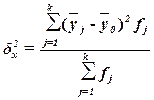 = 1477802564/30 = 349260085,5
= 1477802564/30 = 349260085,5
Определяем
коэффициент детерминации:
ή2 = δ2х / σ2общ = 349260085,56/384755555,56= 0,9077 или 90,77%
Вывод. 90,77%
вариации среднегодовой заработной платы обусловлено вариацией
фондовооруженности труда, а 9,33% – влиянием прочих неучтенных факторов.
Задание 3
1. Определение ошибки
выборки для величины среднесписочной численности менеджеров, а также границ, в
которых будет находиться генеральная средняя
Применяя
выборочный метод наблюдения, необходимо рассчитать ошибки выборки (ошибки
репрезентативности), т.к. генеральные и выборочные характеристики, как правило,
не совпадают, а отклоняются на некоторую величину ε.
Принято
вычислять два вида ошибок выборки - среднюю 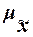 и предельную
и предельную 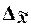 .
.
Для
расчета средней ошибки выборки 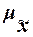 применяются различные
формулы в зависимости от вида и способа отбора единиц из генеральной
совокупности в выборочную.
применяются различные
формулы в зависимости от вида и способа отбора единиц из генеральной
совокупности в выборочную.
Для
собственно-случайной
и механической
выборки с бесповторным способом отбора средняя
ошибка 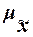 для выборочной средней
для выборочной средней
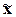 определяется по
формуле
определяется по
формуле
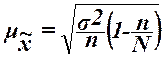 ,
,
где 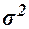 –
общая дисперсия изучаемого
признака,
–
общая дисперсия изучаемого
признака,
N – число единиц в генеральной совокупности,
n – число единиц в выборочной совокупности.
Предельная
ошибка выборки 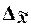 определяет границы, в
пределах которых будет находиться генеральная средняя:
определяет границы, в
пределах которых будет находиться генеральная средняя:
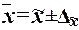 ,
,
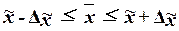 ,
,
где 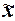 – выборочная средняя,
– выборочная средняя,
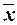 – генеральная средняя.
– генеральная средняя.
Предельная
ошибка выборки 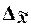 кратна средней ошибке
кратна средней ошибке 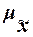 с коэффициентом кратности t (называемым также коэффициентом доверия):
с коэффициентом кратности t (называемым также коэффициентом доверия):
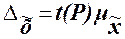
Коэффициент
кратности t зависит от значения
доверительной вероятности Р,
гарантирующей вхождение генеральной средней в интервал 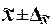 , называемый доверительным интервалом.
, называемый доверительным интервалом.
Наиболее
часто используемые доверительные вероятности Р и соответствующие им значения t задаются следующим образом
(табл. 2.4):
Таблица 3.1
|
Доверительная вероятность P
|
0,683
|
0,866
|
0,954
|
0,988
|
0,997
|
0,999
|
|
Значение t
|
1,0
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
По условию выборочная совокупность насчитывает 30 предприятий,
выборка 20% механическая, следовательно, генеральная совокупность включает 150
предприятий. Выборочная средняя 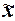 , дисперсия
, дисперсия 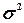 определены
в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи,
представлены в табл. 2.5:
определены
в Задании 1 (п. 3). Значения параметров, необходимых для решения задачи,
представлены в табл. 2.5:
Таблица 3.2
|
Р
|
t
|
n
|
N
|
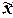
|
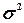
|
|
0,954
|
2
|
30
|
150
|
78560
|
366649779
|
Рассчитаем среднюю ошибку выборки:

Рассчитаем предельную ошибку выборки:
Δ x = t ·μ x
= 2 ·3126,87 = 6253,74
руб.
Определим доверительный интервал для
генеральной средней:
78560-6253,74
≤ Х ≤ 78560+6253,74
72306,26
≤ Х ≤ 84813,74
Вывод. На основании проведенного
выборочного обследования с вероятностью 0,954 можно утверждать, что для
генеральной совокупности предприятий средняя величина среднегодовой заработной
платы находится в пределах от 72306,26 до 84813,74 рублей.
2. Определение ошибки выборки для доли предприятий со среднегодовой
заработной платой 86,4 тыс. руб. и более, а также границ, в которых будет
находиться генеральная доля
Доля
единиц выборочной совокупности, обладающих тем или иным заданным свойством,
выражается формулой
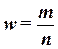 ,
,
где m – число единиц совокупности, обладающих заданным свойством;
n – общее число единиц в совокупности.
Для
собственно-случайной
и механической
выборки с бесповторным способом отбора предельная ошибка выборки 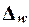 доли единиц,
обладающих заданным свойством, рассчитывается по формуле
доли единиц,
обладающих заданным свойством, рассчитывается по формуле
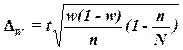 ,
,
где w – доля
единиц совокупности, обладающих заданным свойством;
(1-w) – доля
единиц совокупности, не обладающих заданным свойством,
N – число единиц в генеральной совокупности,
n– число единиц в выборочной совокупности.
Предельная
ошибка выборки 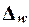 определяет границы, в
пределах которых будет находиться генеральная доля р единиц, обладающих
исследуемым признаком:
определяет границы, в
пределах которых будет находиться генеральная доля р единиц, обладающих
исследуемым признаком:
w – Δw ≤ p ≤ w + Δw
По
условию Задания 3 исследуемым свойством фирм является равенство или превышение
среднегодовой заработной платы 86,40 тыс. руб.
Число
предприятий с данным свойством определяется из табл. 1.4 (графа 3): m=9
Рассчитаем
выборочную долю:
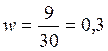
Рассчитаем
предельную ошибку выборки для доли:
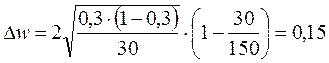
Определим доверительный интервал
генеральной совокупности:
w – Δw ≤ p ≤ w + Δw
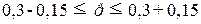
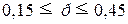
Или
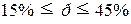
Вывод. С вероятностью 0,954 можно
утверждать, что в генеральной совокупности предприятий доля предприятий со
среднегодовой заработной платой 86,4
тыс. руб. и более будет находиться в пределах от 15% до 45%.
Задание 4
Все недостающие показателя рада динамики определены в табл
4.1 и занесены в таблицу 4.2.
Для
расчетов использовались формулы:
Абсолютный прирост: D= yn
– yn-1
Темп роста: Тр= yn/ yn-1 ·100%
Темп прироста: ТD= Тр – 100
Абсолютное содержание 1%
прироста: А%= yn-1/100
Построим
график выпуска продукции

Осуществим прогноз выпуска
продукции на ближайшие 2 года с помощью среднего абсолютного прироста.
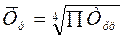 ,
,
где П Трц – произведение
темпов роста цепных
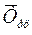 =
= 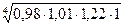 =
= 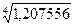 =
= 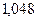 104,8%
104,8%
Прогнозируемый
выпуск продукции за 2003 год:
22,18
·1,048 = 23,24 млн. руб.
Прогнозируемый
выпуск продукции за 2004 год:
23,24
·1,048 = 24,36 млн. руб.
Вывод. По данным
прогноза средний темп роста выпуса продукции будет составлять 104,8%, что в
2003 году будет составлять 23,24 млн. рублей, а в 2004 году – 24,36 млн.
рублей, что свидетельствует о ежегодном увеличении выпуска продукции.
Аналитическая
часть
Для
проведения исследования в аналитической части курсовой работы, были взяты
статистические материалы Госкомстата РФ (с сайта www.gks.ru), отражающие динамику
внешней торговли Российской Федерации.
Аналитический
раздел данной работы выполнен в программе MS Excel (так же,
как практическая часть курсовой работы).
Статистика
внешней торговли является одной из важнейших областей экономической статистики.
Информация, отражающая развитие внешней торговли, является важным инструментом
для принятия торгово-политических решений и эффективного управления
внешнеэкономическими связями.
Под внешней торговлей понимается ввоз и
вывоз товаров. Основными задачами статистики внешней торговли являются
разработка системы показателей, характеризующих размеры, динамику и структуру
внешней торговли, анализ факторов, обусловливающих основные тенденции их
развития.
Для анализа статистики внешней торговли
используется такие категории, как импорт и экспорт.
Под экспортом понимается вывоз
из страны произведенных, выращенных или добытых товаров отечественного
производства. При этом к товарам отечественного происхождения относятся также
товары иностранного происхождения, которые ввозятся в страну и подвергаются
переработке, изменяющей их основные качественные или технические
характеристики, и реэкспорт. В результате экспорта товаров уменьшаются
национальные запасы материальных ценностей.
Под импортом понимается ввоз
товаров в страну. В импорт включаются ввезенные товары, предназначенные для
потребления внутри страны, реэкспорта, и товары, закупаемые для отечественных
организаций за границей. В результате импорта товаров увеличиваются национальные
запасы материальных ценностей.
Для более детального анализа динамики и
структуры внешней торговли России составим таблицы, характеризующие динамику
внешней торговли страны с 2003 по 2006 гг. и рассчитаем на основе данных таблиц
все показатели динамики.
|
|
|
|
|
|
|
|
|
Таблица 1
|
|
Внешняя
торговля Российской Федерации
|
|
|
Экспорт
|
Импорт
|
|
2003
г.
|
2004
г.
|
2005г.
|
2006
г.
|
2003
г.
|
2004
г.
|
2005
г.
|
2006
г.
|
|
ВСЕГО, млн.
долл.
|
135929
|
183207
|
243798
|
303926
|
76070
|
97382
|
125434
|
164692
|
|
|
|
|
|
|
|
|
|
|
Для анализа
динамики внешней торговли России рассчитаем:
а)
среднегодовой объем экспорта и импорта за 2003-2006 гг.;
б)
абсолютные приросты по годам и к 2003
г.;
в) темпы
динамики: цепные и базисные (к 2003
г.);
г)
абсолютное содержание одного процента прироста (снижения).
Полученные
показатели представим в таблице;
д)
среднегодовые темпы экспорта и импорта за 2003-2006 гг. Построим график
среднегодового объема экспорта и импорта за 2003-2006 гг. По исчисленным
показателям сформируем выводы.
а)
Среднегодовой объем экспорта и импорта (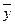 экс и
экс и 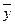 имп) вычислим по формуле средней арифметической
простой:
имп) вычислим по формуле средней арифметической
простой:
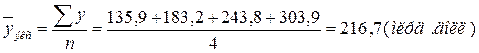 ,
,
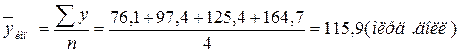
Для расчета
пунктов б, в, г, скопируем
практическую часть данной курсовой работы, но заменим показатели значениями,
взятыми из материалов Госкомстата России, с целью показать, как работают
программные материалы, разработанные в ходе решения практической части, на
реальных примерах. Заменяя значения на данные таблицы 3, а также взяв за базис 2003 г., показатели динамики
(введенные ранее формулы) посчитаются автоматически, и результаты буду
выглядеть следующим образом:
|
|
|
|
|
|
|
|
|
Таблица 2
|
|
Аналитические
показатели динамики экспорта России за 2003-2006 гг.
|
|
Год
|
Экспорт, млрд.
долл.
|
Абсолютные
приросты, млрд. долл.
|
Темпы роста, %
|
Темпы прироста,
%
|
Абсолютные
содержания 1% прироста (снижения), млрд.долл.
|
|
цепные
|
базисные
|
цепные
|
базисные
|
цепные
|
базисные
|
|
2003
|
135,9
|
_
|
_
|
_
|
100
|
_
|
_
|
_
|
|
2004
|
183,2
|
47,3
|
47,3
|
134,8
|
134,8
|
34,8
|
34,8
|
1,359
|
|
2005
|
243,8
|
60,6
|
107,9
|
133,1
|
179,4
|
33,1
|
79,4
|
1,832
|
|
2006
|
303,9
|
60,1
|
168
|
124,7
|
223,6
|
24,7
|
123,6
|
2,438
|
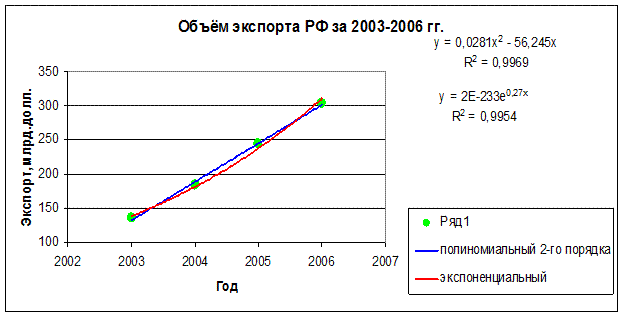
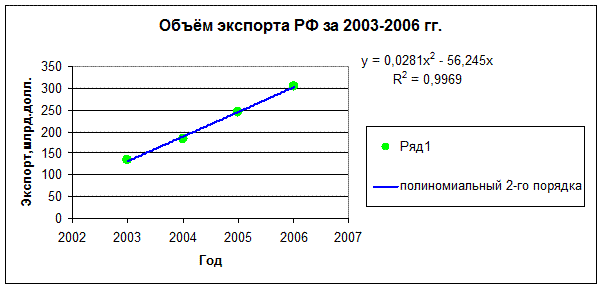
|
|
|
|
|
|
|
|
|
Таблица 3
|
|
Аналитические
показатели динамики импорта России за 2003-2006 гг.
|
|
Год
|
Импорт,
млрд.долл
|
Абсолютные
приросты,млрд.долл
|
Темпы роста,%
|
Темпы
прироста,%
|
Абсолютные
содержания 1% прироста (снижения),млрд.долл.
|
|
цепные
|
базисные
|
цепные
|
базисные
|
цепные
|
базисные
|
|
2003
|
76,1
|
_
|
_
|
_
|
100
|
_
|
_
|
_
|
|
2004
|
97,4
|
21,3
|
21,3
|
128
|
128
|
28
|
28
|
0,761
|
|
2005
|
125,4
|
28
|
49,3
|
128,7
|
164,8
|
28,7
|
64,8
|
0,974
|
|
2006
|
164,7
|
39,3
|
88,6
|
131,3
|
216,4
|
31,3
|
116,4
|
1,254
|
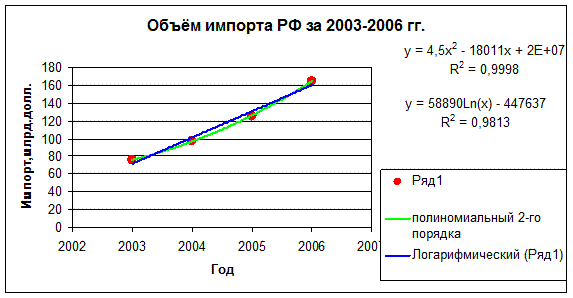
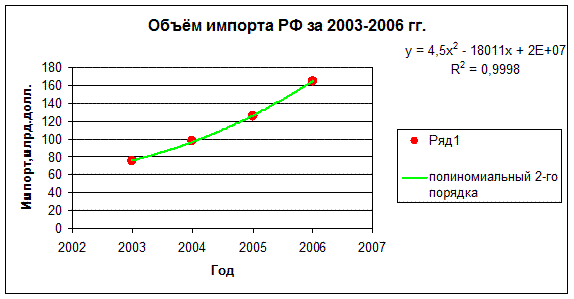
Определим среднегодовые темпы роста
экспорта и импорта Российской Федерации за 2004-2006 гг., используя формулу:
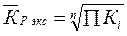 =
= 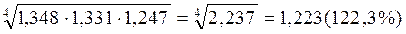 ,
,
а также среднегодовой темп прироста
экспорта с 2004-2006 гг.:
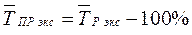 =
=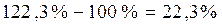 .
.
Для
импорта:
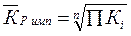 =
= 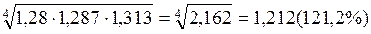 ,
,
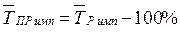 =
=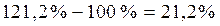 .
.
За
базу сравнения мы взяли 2003
г., тем самым показали, что за период с 2003 г. по 2006 г. экспорт России
увеличился на 78,2 млрд. долл., а импорт – на 49,9 млрд. долл., т.е.
товарооборот прирастал больше за счет увеличения экспорта. Базисный абсолютный
прирост как экспорта, так и импорта России постоянно увеличивался.
Анализируя
данные цепного абсолютного прироста экспорта за 2004-2006 гг., можно сделать
следующий вывод: наибольший прирост экспорта наблюдался в 2005 году (60,6 млрд.
долл.), а наименьший прирост - в 2004 году (47,3 млрд. долл.). В среднем
же за год экспорт прирастал на 56 млрд. долл. Об этой тенденции свидетельствуют
и относительные показатели. В 2004, 2005 гг. темп роста экспорта постоянно
увеличивался по сравнению с 2003 годом, и в 2006 г. составил 223,6%. Из
приведенных данных по цепному темпу роста видно следующее: самый высокий темп
роста по сравнению с предыдущим годом был в 2004 году (134,8%), а самый
низкий - в 2006 году (124,7%). Среднегодовой коэффициент роста экспорта
составил 1,223. Рассмотрим коэффициенты и темпы прироста экспорта. Базисный
коэффициент прироста увеличивался неравномерно. По сравнению с 2000 годом
коэффициент прироста экспорта в 2004 году составил 0,348, а в 2006 году – 1,236.
Данные по цепному темпу прироста показывают, что ежегодные темпы прироста
колебались от 34,8% в 2004 г.
до 24,7 % в 2006 г.
В среднем же за год экспорт прирастал на 22,3 %. Рассматривая абсолютное
значение 1% прироста можно заметить, что данный показатель был наиболее высоким
в 2006 году (2,44 млрд. долл.), наиболее низким в 2004 г. (1,36 млрд. долл.)
Далее
рассмотрим динамику импорта. Как видно из приведенных данных, объем импорта
России за изучаемый период возрастал, при этом наибольший прирост импорта
наблюдался в 2006 году (39,3 млрд. долл.), а наименьший прирост - в 2004
году (21,3 млрд. долл.). В среднем же за год импорт прирастал на 29,5 млрд.
долл. Об этой тенденции свидетельствуют и относительные показатели.
Рассмотрим
коэффициенты и темпы роста импорта. В 2004, 2005, 2006 гг. темп роста постоянно
увеличивался по сравнению с 2003 годом и в 2006 г. составил 216,4%. Из
приведенных данных по цепному темпу роста видно следующее: самый высокий темп
роста по сравнению с предыдущим годом был в 2006 году (216,4%), а самый
низкий - в 2004 году (128%). Среднегодовой коэффициент роста импорта
составил 1,212. Рассмотрим коэффициенты и темпы прироста импорта. Базисный
коэффициент прироста неравномерно увеличивался. По сравнению с 2004 годом
коэффициент прироста импорта в 2005 году составил 0,359, а в 2004 году – 1,111.
Данные по цепному темпу прироста показывают, что ежегодные темпы прироста
колебались от 28% в 2004 г.
до 31,3% в 2006 г.
В среднем же за год импорт прирастал на 21,2%. Абсолютное значение 1% прироста
объема импорта с каждым годом увеличивалось. Если в 2004 году оно равнялось 0,761
млрд. долл., то в 2006 году – 1,254 млрд. долл.
Как
видно из вышеизложенного, анализ показателей ряда динамики импорта и экспорта
позволяет воссоздать более полную картину динамики внешней торговли России за
период 2003-2006 гг., предоставляя информацию о том, на сколько млрд. долл. в
год увеличивались импорт и экспорт, какими темпами они растут, каковы
коэффициенты роста и прироста.
Заключение
В настоящее
время в современных непростых условиях
российской экономики качественный анализ результатов производственной
деятельности приобретает, наряду с составлением качественных прогнозов
дальнейшего развития приобретает особо важное значение. Таким образом, одной из
важнейших задач статистики становится
изучение изменения различных показателей во времени.
Исследовать динамику
можно при помощи рядов динамики. Анализ же интенсивности изменения явления во
времени осуществляется при помощи как абсолютных показателей (абсолютный
прирост, темп роста, темп прироста, абсолютное значение одного процента
прироста), так и относительных (средний
абсолютный прирост, средний темп роста, средний темп прироста).
Именно при помощи этих показателей выявляется общая тенденция
развития того или иного явления (тренд). Выявление и характеристика трендов и
моделей взаимосвязи в свою очередь создают базу для прогнозирования, столь
необходимого для дальнейшего развития производства.
Список используемой литературы
1. Башкатов
Б.И. Социально-экономическая статистика: учеб. – М., Изд-во Юнити, 2002.
2. Громыко Г.Л. Теория статистики: учеб. –
М., Изд-во Инфра-М, 2000.
3. Гусаров
В.М. Социально-экономическая статистика: учеб. – М., Изд-во Юнити, 2001
4. Гусаров
В.М. Теория статистики: учеб. – М., Изд-во Юнити, 1998.
5. Салин В.Н. Статистика финансов: учеб. –
М., Изд-во Финансы и статистика, 2000.
6. Салин В.Н., Шпаковская Е.П. Социально-экономическая
статистика: учеб. – М.: Изд-во Юритъ, 2001.
7. Симчера В.М. Практикум по статистике:
учеб. пособ. – М. Изд-во Финстатинформ, 1999.
8. Шмойкова
Р.А. Практикум по теории статистики: учеб. пособ. – М., Изд-во Финансы и статистика, 2002.
[1] Товарная продукция
охватывает стоимость не всей произведенной в отчетном периоде продукции, а
только той ее части, которая отпущена или предназначена к отпуску на сторону. В.П. Салин
“Социально-экономическая статистика”: учебник, М., Юристъ – 2001. С.230.