МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ

В РЕГИОНАЛЬНЫХ ХОЗЯЙСТВЕННЫХ СИСТЕМАХ

Бияков О.А.,

к.э.н., доцент,

г. Кемерово, Кузбасский государственный технический университет

Исследование динамики развития экономических систем различного уровня подразумевает наличие инструментария, способного адекватно отражать в модели процесс этого развития. Специфической чертой моделирования экономических процессов является отсутствие возможности проведения эксперимента на основе полученной модели. Как правило, конечной целью моделирования выступает формирование некоторого набора критериальных признаков, которые используются в процессе принятия будущих решений. Другая особенность моделирования экономических процессов определяется спецификой исходной информации для построения модели. В большинстве случаев эта информация представлена в виде временных рядов по некоторым параметрам исследуемого объекта. В большинстве случаев длина таких рядов ограничивается 10 – 12 временными интервалами. Адекватность же модели определяется качеством исходной информации и ее количественным представлением. При исследовании технических систем достаточно широко применяются процедуры интерполирования, позволяющие в некоторых случаях компенсировать качество исходной информации увеличением ее количества. Для экономических систем этот подход не приемлем, так как большинство процессов, протекающих в них, имеют строго детерминированный характер. Система позволяет фиксировать свои параметры только в определенные ее структурой моменты времени, а в промежутке между ними находится в состоянии неопределенности с точки зрения исследователя. Это позволяет сделать вывод о проблематичности улучшения качества модели за счет количественной составляющей исходной информации, полученной путем интерполирования. Другими словами, уже в модели должны быть достаточно полно заложены тенденции развития системы, попытки же компенсировать качество модели количеством исходной информации могут привести к большим искажениям значений результирующих параметров модели.

Подавляющее большинство исследований экономических систем в своей основе используют весьма ограниченный базовый набор типовых моделей: полиномиальную, логарифмическую, логистическую, функцию Гомпертца и некоторые другие. Данные модели, за исключением первой, достаточно хорошо описывают процессы с постепенно возрастающими темпами роста в начальной стадии развития и постепенно затухающими темпами роста в конце, однако такие процессы могут протекать лишь в идеализированной экономической среде. Вторая производная в этих моделях монотонно убывает на всем диапазоне исследования, что позволяет усомниться в адекватности модели реальной действительности. Единственный вопрос, на который могут дать ответ упомянутые модели – это общая тенденция развития системы, но не более того. Попытки выделения влияния отдельных факторов на общие процессы, описываемые такими моделями, на практике обречены на провал.

В практических исследованиях достаточно часто используется полиномиальная модель. Она лишена некоторых недостатков рассмотренных моделей, в частности упомянутых проблем с монотонно затухающим значением второй производной. Однако и она достаточно условно описывает экономические процессы, одним из свойств которых является цикличность. Отражение этого свойства возможно в этой модели степенью полинома 9 – 14. Естественно, что интерпретация получаемых параметров модели теряет всякий экономический смысл уже на полиноме пятой степени. С другой стороны, попытки описания сложных явлений квадратичным или кубическим полиномом, как это практикуется многими исследователями, не выглядят достаточно убедительными.

Особое положение в списке базовых занимает семейство моделей, основанных на применении рядов Фурье. Как не парадоксально, использование этих моделей для анализа экономических процессов до сих пор не получило широкого распространения, хотя для аппроксимации коэффициентов ряда Фурье существует достаточно много хорошо разработанных численных методов. На наш взгляд, причина такого положения заключается в высокой степени консерватизма исследователей от экономики.

         Краткий обзор подходов к моделированию экономических процессов на основе анализа временных рядов позволяет заключить следующее. В большинстве исследований процесс моделирования сводится к нахождению тренда, циклическая и случайная составляющие остаются за рамками модели. Проблемы «белого шума» как таковые вообще не рассматриваются, либо в модели появляется составляющая, которая берет на себя все многообразие понятия «белый шум» и, как следствие, имеет чисто формальный характер. Особо следует остановиться на циклической составляющей. В традиционной интерпретации она описывает «длительные периоды относительного подъема и спада» [1, с.356]. Подобное упрощение понятия конечно же позволяет описать процесс простейшей моделью, но она не будет иметь ничего общего с действительностью. В моделях, претендующих на описание экономических процессов, цикличность должна учитываться в самом тренде, составлять его формальную основу. В этом случае понятие цикличности наполняется иным содержанием, которое отражается в сути модели, а не в форме, под которую подгоняется исходная информация для обработки некоторой элементарной моделью.

Другой проблемой, связанной с моделированием экономических процессов, является то, что априори предполагается стационарность процесса. Это – глубокое заблуждение. Процесс, описываемый циклической составляющей, у которой в свою очередь циклически изменяется фаза и амплитуда, не может по своей сути быть стационарным. Это подтверждается многими исследованиями, основанных на Wavelet-анализе [2,3] и волнах Эллиотта (Elliott) [4,5]. К сожалению, это направление достаточно хорошо разработано лишь для анализа финансовых рынков и пока практически не используется для изучения других аспектов экономических процессов.

Общей проблемой перечисленных стандартных подходов к моделированию является неявное сведение реального процесса к стационарному. Подтверждением этому может служить и то, что в основе данных моделей лежит аддитивная составляющая в интерпретации временного ряда. Можно предположить, что использование модели мультипликативного вида позволит увеличить адекватность модели реальной ситуации.

Данное предположение подтверждается проведенными экспериментами. В качестве аддитивной модели возьмем за основу ряд Фурье:

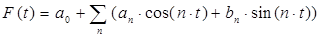              (1)

В качестве мультипликативной предлагается разработанная нами модель:

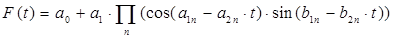                    (2)

Для модели (1) аргументы тригонометрических функций взяты в классическом представлении, для модели (2) – более детально. Отметим, что расчеты производились при различном представлении аргументов функций, но это практически не отразилось на получаемых результатах. Расшифровка аргументов в модели (2) диктовалась последующей необходимостью экономической интерпретации параметров модели, попыткой выделения Найквистовой (основной) частоты и фазы смещения.

Для проведения расчетов использовались процедуры нелинейного оценивания, входящие в пакет Statistica 5.0 for Windows. В качестве исходной информации взят показатель выработки электроэнергии в Кузбассе за 1996-2002 гг. Исходные данные были подвергнуты процедуре медианного сглаживания, разработанную автором.

Процедуры сглаживания временных рядов достаточно часто применяются при обработке разнообразных статистических данных в экономических исследованиях. Основной целью такой обработки является выделение тренда и уменьшение уровня белого шума. Известно достаточно много процедур сглаживания временных рядов, но наиболее часто используются процедуры скользящего среднего и экспоненциального сглаживания, которые дают удовлетворительные результаты при достаточно большом наборе значений того или иного показателя.

Для первичной обработки временных рядов предлагается новая процедура сглаживания – медианная. Пусть дан временной ряд, 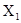,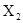…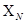, тогда каждый новый элемент сглаженного ряда 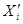вычислим как

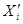                                  = 1 + (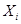- Me)/(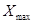- 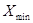+ 1),        i=1..N,          (3)

где – Me – медиана временн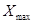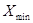ого ряда,  ,  - максимальный  и минимальный члены временного ряда.

Предлагаемый метод имеет ряд достоинств. Во-первых, уменьшается  общая погрешность преобразования. Если рассчитывать эту погрешность через интегральную оценку, то при медианном сглаживании имеем приблизительно 4%, скользящем - 8%, экспоненциальном - 11%. Во-вторых, при медианном сглаживании практически отсутствует смещение по локальным экстремумам. В-третьих, при попытке аппроксимации исходных данных и данных, сглаженных по медиане, имеем практически одинаковый вид функции.

Следует отметить еще одно преимущество метода, которое имеет отношение непосредственно к моделированию экономических процессов. Во временных рядах, отражающих протекающие экономические процессы, достаточно часто встречаются нулевые и отрицательные компоненты. Допустим, необходимо определить темпы роста – возникает проблема деления. При расчете темпов роста после медианного сглаживания в преобразованном временном ряде отсутствуют нулевые и отрицательные компоненты при практически полном совпадении данного тренда с исходным. Ни один из других рассматриваемых преобразований не дает такого результата. Таким образом решается проблема с нулевыми компонентами, когда темп роста рассчитать нельзя, и отрицательными - когда темп роста имеет отрицательный знак, а сам такой показатель - весьма загадочное экономическое содержание. Кроме этого в преобразованном временном ряде практически полностью отсутствует фазовый сдвиг, что обеспечивается процедурой нормирования данных.

Исходные данные, прошедшие процедуру медианного сглаживания, представлены в табл.1.

                           Таблица 1

Янв.

Февр.

Март

Апр.

Май

Июнь

Июль

Авг.

Сент.

Окт.

Нояб.

Дек.

1996

1,370

1,178

1,239

1,053

0,766

0,613

0,567

0,591

1,183

0,896

1,044

1,127

1997

1,060

0,957

1,001

0,809

0,732

0,594

0,564

0,565

0,722

0,986

1,224

1,446

1998

1,451

1,368

1,386

1,116

0,999

0,638

0,583

0,558

0,692

0,846

0,911

1,226

1999

1,440

1,262

1,376

0,660

0,555

0,555

0,555

0,572

0,660

1,186

1,291

1,442

2000

1,454

1,346

1,370

1,224

1,003

0,764

0,578

0,532

0,869

1,068

1,221

1,167

2001

1,268

1,080

0,983

0,752

0,456

0,503

0,520

0,515

0,599

1,137

1,244

1,323

2002

1,387

1,223

1,288

1,111

0,904

0,550

0,455

0,525

0,669

1,150

1,258

1,388

         Для аппроксимации коэффициентов в (1) и (2) использовались методы Хука-Дживса и Ньютона (Quasi-Newton). В процессе эксперимента выяснилось, что метод Ньютона дает более устойчивые результаты, менее зависим от начальных условий процесса аппроксимации, что связано с достаточно удачной процедурой анализа сходимости значений вторых производных. Все результаты, приведенные ниже, были получены с помощью метода Ньютона по критерию минимизации суммы квадратов отклонений.

         Расчеты проводились для (1) и (2) на различном числе гармоник (от 2 до 7). Для (1) число гармоник оказалось не критичным, для второй модели наилучшие результаты были получены на 6 гармониках, однако, уже при включении в (2) пяти гармоник наблюдался резкий рост a1 по экспоненциальной зависимости, что затрудняет его экономическую интерпретацию при анализе реальных ситуаций.

         Результаты расчетов коэффициентов по модели (1) на трех гармониках приведены в табл.2.

                                                                                                                 Таблица 2

a0

a1

b1

a2

b2

a3

b3

0,957

-0,012

0,047

-0,012

0,006

-0,002

0,012

Сумма квадратов отклонений составила 8,417. Следует отметить, что эта величина практически не зависит от количества гармоник, включенных в (1). Число итераций процесса аппроксимации коэффициентов в (1) составило от 78 до 136 в зависимости от числа гармоник и стартовых значений коэффициентов.

         Результаты расчетов коэффициентов по модели (2) на трех гармониках приведены в табл.3.                                                                                                                                                                                

                                                                                                                       Таблица 3

a0

a1

a11

a21

b11

b21

a12

a22

b12

b22

a13

a23

B13

b23

0,933

-0,891

0,146

0,381

-3,438

0,318

0,146

0,381

-3,438

0,318

0,146

0,381

-1,137

0,144

Сумма квадратов отклонений составила 4,827. Это почти вдвое лучше результата по (1). Число итераций процесса аппроксимации коэффициентов в (2) составило от 32 до 84 в зависимости от числа гармоник и стартовых значений коэффициентов. Кроме того, численные значения коэффициентов в (2) очевидно более приемлемы для экономической интерпретации процесса. Именно для этого в модели (2) дается более детальная расшифровка аргументов тригонометрических функций.

         Результаты аппроксимации достаточно хорошо иллюстрируют гистограммы распределения остатков, приведенные на рисунках 1 и 2.

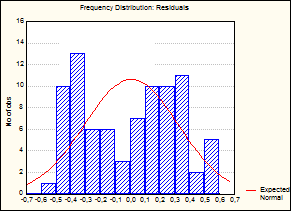
Рис.1. Гистограмма распределения

остатков при аппроксимации по (1)
 

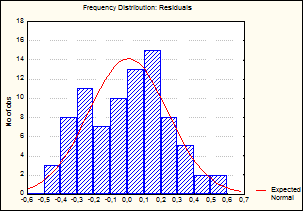
Рис.2. Гистограмма распределения

остатков при аппроксимации по (2)
 
 

                  

                  

         Преимущество мультипликативной модели перед аддитивной подтверждается и геометрической интерпретацией результатов, показанных на рисунке 3, где утолщенной линией показаны исходные данные, тонкой линией – результаты по аддитивной модели, пунктиром – по мультипликативной.
 
 

Рис.3. Геометрическая интерпретация результатов по моделям (1) и (2)

         Эксперимент проводился над несколькими десятками временных рядов, содержащих от 12 до 96 компонент, отражающих различные аспекты функционирования экономики Кузбасса. В подавляющем большинстве случаев получены устойчивые результаты, позволяющие говорить о наличии микроциклов в экономической системе, по крайней мере на уровне региона. Одним из свидетельств этого является тот факт, что далеко не всегда количество гармоник в модели определяет ее адекватность. При расчетах на модели (2), содержащей две гармоники были получены результаты, превосходящие те, которые приведены в таблице 3. Это можно видеть по практически идеальному распределению остатков (рис.4).                                             

Результаты аппроксимации модели (2) на двух гармониках представлены в табл.4.

       Обращает на себя внимание определенная закономерность результатов, приведенных в таблицах 3 и 4. Для модели (2) коэффициенты косинусоидальной составляющей в трех гармониках совпадает с точностью до пятого знака

(a11=a12=a13 и a21=a22=a23).

Аналогичная ситуация для

 

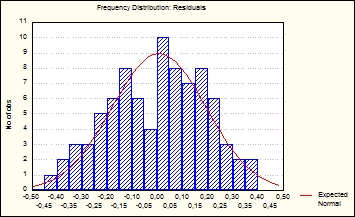
Рис.4. Распределение остатков при аппроксимации мультипликативной модели на двух гармониках
 
                                                                              

модели с двумя гармониками (см. табл.4). Коэффициенты в синусоидальной составляющей частично совпадают по двум первым гармоникам из трех. То же можно увидеть на коэффициентах модели с двумя гармониками (b21=b22) в табл.4.

                                                                                                                       Таблица 4

a0

a1

a11

a21

b11

b21

a12

a22

b12

b22

0,95205

1,17655

0,53093

-0,07535

0,39884

-0,26399

0,53093

-0,07535

2,00418

-0,26302

         Подобная закономерность прослеживается при экспериментах с моделями, содержащими до 7 гармоник. Объяснение данного факта с точки зрения экономической интерпретации пока не получено. Однако эксперименты позволили упростить модель (2) без потери ее качества и свести ее к следующему виду

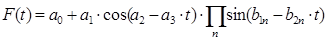        (4)

Подмеченные закономерности в аппроксимированных коэффициентах мультипликативных моделей позволяют формализовать проблему количества гармоник, включаемых в модель. В качестве критерия можно предложить любую форму оценки степени совпадения получаемых соответствующих коэффициентов по семейству моделей с различным числом гармоник.

Использование предлагаемых мультипликативных моделей (2) и (4) позволяет достаточно точно описывать процессы, происходящие в экономических системах, информация о которых представлена в виде временных рядов.

Литература

1. Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере.- М.:Инфра , 1998. – 528 с.

2. Guido J. Deboeck, Tuevo K. Kohonen. Visual Explorations in Finance: With Self-Organizing Maps (Springer Finance). – Paris, 1998            3. R. Prechter. At The Crest of The Tidal Wave. – London, 1994

4. A. Balan. Elliott Wave as Applied to Foreign Exchange. – London, 1992

5. R. Prechter. Elliott Wave Principle. – London, 1991