Лабораторная
работа № 6. РЯДЫ ДИНАМИКИ. АНАЛИТИЧЕСКАЯ МОДЕЛЬ СЕЗОННЫХ И СЛУЧАЙНЫХ ИЗМЕНЕНИЙ.
ИНДЕКСЫ СЕЗОННОСТИ.
Цель работы: Выявление
аналитической закономерности выровненных рядов динамики, учитывающих сезонную и
случайные изменения во времени признаков ряда. Рассчитать индексы
сезонности.
Задание. Используя данные о выпуске
продукции предприятием за двенадцать месяцев (табл. 1) найти аналитические
тригонометрические модели динамического ряда. Соответствующие модели
представить графиками. Сравнить полученные результаты. Вычислить индексы
сезонности. Сделать выводы.
Условие. Имеются сведения о произведенной
продукции предприятием за год (табл. 1).
Таблица 1
|
п/п
|
Месяцы
|
Выпуск продукции, млн. руб.
|
|
1
|
2
|
3
|
|
1
|
Январь
|
33
|
|
2
|
Февраль
|
24
|
|
3
|
Март
|
52
|
|
4
|
Апрель
|
32
|
|
5
|
Май
|
33
|
|
6
|
Июнь
|
57
|
|
7
|
Июль
|
96
|
|
8
|
Август
|
107
|
|
9
|
Сентябрь
|
92
|
|
10
|
Октябрь
|
109
|
|
11
|
Январь
|
53
|
|
12
|
Февраль
|
75
|
Выполнение
задания.
1.
Аналитическая модель основного тренда, сезонной
и случайной компонент динамического ряда
Анализ колеблемости
динамических рядов наряду с выделением
случайных колебаний требует изучения
периодических колебаний. Изучение периодических («сезонных») колебаний
необходимо с целью исключения их влияния на
общую динамику для выявления «случайной» колеблемости.
Выделение
сезонного периода можно выполнить на основе построения аналитической модели
проявления сезонных колебаний. Построение аналитической модели выявляет
основной закон колеблемости данного временного ряда в связи с переходом от
месяца к месяцу и дает среднюю характеристику внутригодичных колебаний.
При
исследовании явлений периодического типа в качестве аналитической формы
развития во времени принимается метод Фурье, разложения в ряд по
фундаментальной системе тригонометрических функций
:
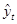= а0 + 
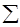(ak cos kt+
bk sin kt). (1)
В этой
зависимости величина k определяет гармонику ряда Фурье и
может быть взята с разной степенью точности (чаще всего от 1 до 4). Для
отыскания параметров нового ряда (1) используется метод наименьших квадратов,
т.е.
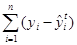= min .
(2)
Справедливы
следующие формулы для вычисления параметров:
a0 =
;
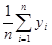ak =
;
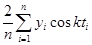(3)
bk =
;
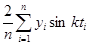Для изучения сезонных колебаний на
протяжении года необходимо взять n=12 (по числу месяцев в году). Тогда, представляя
периоды как части длины окружности, ряд динамики можно записать в следующем
виде:
Таблица 2
|
Период
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
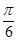
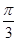
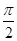
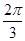
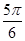
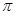
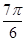
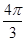
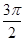
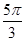
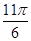
Признак
|
у0
|
у1
|
у2
|
у3
|
у4
|
у5
|
у6
|
у7
|
у8
|
у9
|
у10
|
у11
|
Для
вычисления синусов и косинусов разных гармоник лучше всего пользоваться табл.
3.
Таблица 3
|
t
|
cos t
|
cos 2t
|
cos 3 t
|
cos 4t
|
sin t
|
Sin 2t
|
sin 3t
|
sin 4t
|
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
|
|
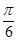
0,866
|
0,5
|
0
|
-0,5
|
0,5
|
0,866
|
1
|
0,866
|
|
|
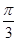
0,5
|
-0,5
|
-1
|
-0,5
|
0,866
|
0,866
|
0
|
-0,866
|
|
|
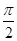
0
|
-1
|
0
|
1
|
1
|
0
|
-1
|
0
|
|
|
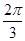
-0,5
|
-0,5
|
1
|
-0,5
|
0,866
|
-0,866
|
0
|
0,866
|
|
|
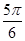
-0,866
|
0,5
|
0
|
-0,5
|
0,5
|
-0,866
|
1
|
-0,866
|
|
|
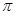
-1
|
1
|
-1
|
1
|
0
|
0
|
0
|
0
|
|
|
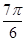
-0,866
|
0,5
|
0
|
-0,5
|
-0,5
|
0,866
|
-1
|
0,866
|
|
|
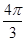
-0,5
|
-0.5
|
1
|
-0,5
|
-0,866
|
0,866
|
0
|
-0,866
|
|
|
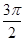
0
|
-1
|
0
|
1
|
-1
|
0
|
1
|
0
|
|
|
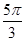
0,5
|
-0,5
|
-1
|
-0,5
|
-0,866
|
-0,866
|
0
|
0,866
|
|
|
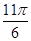
0,866
|
0,5
|
0
|
-0,5
|
-0,5
|
-0,866
|
-1
|
-0,866
|
Для k =1
уравнение (1) примет вид:
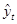= а0 + a1
cos t+ b1 sin t
, (4),
в котором параметры а0, a1 и b1
будут
найдены из соотношений:
a0 =
;
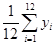a1 =
;
(5)
b1 =
;
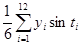Для k =2
уравнение (1) будет таким:
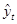= а0 + a1
cos t+ b1 sin t+
a2 cos 2t+ b2 sin 2t , (6),
в котором параметры a2 и b2
определяются
из соотношений:
a2 =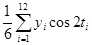 
;
(7)
b2 =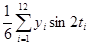 
;
Применим
расчетную схему (4)-(7) к исходной задаче. В результате получим аналитическую
модель динамического ряда для четырех гармоник k =1 ,
k =2 , k =3
и k =4 . Полученные данные представлены
в таблице 4, выполненной в среде Ехсеl.
Из этой
таблицы найдем коэффициенты ряда Фурье
a0 =
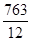= 63,583 ; a1 = 
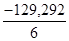= -21,549 ; b1 = 
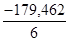= -29,910 ;
a2 =
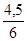= 0,75 ; b2
= 
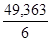= 8,227 ;
a3
= 
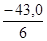= -7,167 ; b3 = 
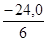= -4,0 ;
a4 = 
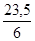= 3,917
; b4 =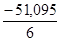 
= -8,516 .
Запишем
соответствующие приближения, подставляя найденные коэффициенты в ряд Фурье (1),
ограничиваясь числами k =1 ,
k =2 , k =3
и k =4 , получим следующие четыре модели
исходного динамического ряда:
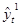= 63,583 - 21,549
cos t - 29,910 sin
t ,
= 63,583 - 21,549
cos t -
29,910 sin t + 0,75
cos 2t+ 8,227
sin 2t , (8)
= 63,583 - 21,549
cos t -
29,910 sin t + 0,75
cos 2t+ 8,227
sin 2t - 7,167
cos 3t - 4 sin
3t ,
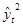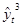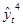= 63,583 - 21,549
cos t -
29,910 sin t + 0,75
cos 2t+ 8,227
sin 2t - 7,167
cos 3t - 4 sin
3t + 3,917
cos 4t - 8,516 sin
4t ,
|
ti
|
yi
|
yicos ti
|
yisin ti
|
|
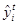
yicos 2ti
|
yisin2ti
|
|
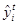
yicos3ti
|
yisin3ti
|
|
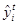
yicos 2ti
|
yisin2ti
|
|
|
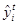
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
0
|
33
|
33,000
|
0,0
|
42,035
|
33,0
|
0,000
|
42,78
|
33,0
|
0
|
35,618
|
33,0
|
0,000
|
39,535
|
|
|
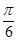
24
|
20,785
|
12,0
|
29,967
|
12,0
|
20,785
|
34,73
|
0,0
|
24
|
26,523
|
-12,0
|
20,785
|
25,657
|
|
|
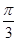
52
|
26,000
|
45,033
|
26,906
|
-26,0
|
45,033
|
34,41
|
-52,0
|
0
|
27,359
|
-26,0
|
-45,033
|
21,942
|
|
|
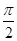
32
|
0,000
|
32,0
|
33,673
|
-32,0
|
0,000
|
41,90
|
0,0
|
-32
|
37,900
|
32,0
|
0,000
|
29,384
|
|
|
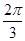
33
|
-16,500
|
28,579
|
48,455
|
-16,5
|
-28,579
|
55,20
|
33,0
|
0
|
55,324
|
-16,5
|
28,579
|
45,990
|
|
|
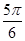
57
|
-49,363
|
28,5
|
67,290
|
28,5
|
-49,363
|
70,75
|
0,0
|
57
|
74,960
|
-28,5
|
-49,363
|
67,311
|
|
|
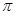
96
|
-96,000
|
0,0
|
85,132
|
96,0
|
0,000
|
84,38
|
-96,0
|
0
|
91,549
|
96,0
|
0,000
|
87,632
|
|
|
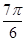
107
|
-92,665
|
-53,5
|
97,200
|
53,5
|
92,665
|
92,44
|
0,0
|
-107
|
100,643
|
-53,5
|
92,665
|
101,510
|
|
|
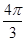
92
|
-46,000
|
-79,674
|
100,261
|
-46,0
|
79,674
|
92,76
|
92,0
|
0
|
99,808
|
-46,0
|
-79,674
|
105,225
|
|
|
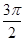
109
|
0,000
|
-109,0
|
93,494
|
-109,0
|
0,000
|
85,27
|
0,0
|
109
|
89,266
|
109,0
|
0,000
|
97,782
|
|
|
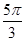
53
|
26,500
|
-45,899
|
78,712
|
-26,5
|
-45,899
|
71,96
|
-53,0
|
0
|
71,843
|
-26,5
|
45,899
|
81,176
|
|
|
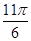
75
|
64,952
|
-37,5
|
59,877
|
37,5
|
-64,952
|
56,41
|
0,0
|
-75
|
52,206
|
-37,5
|
-64,952
|
59,856
|
|
Итого:
|
763
|
-129,292
|
-179,462
|
763,00
|
4,500
|
49,363
|
763,00
|
-43,0
|
-24,0
|
763,0
|
23,5
|
-51,095
|
763,00
|
Таблица 4
В последней строке табл. 4 (гр.
2, 5, 8, 11, 14) представлены фактические и расчетные суммарные уровни выпуска
продукции, по которым наглядно видно, что модель достаточно точно отражает эмпирические
признаки ряда динамики.
2.
Графическое представление аналитических моделей.
Сопоставим выровненные уровни
динамического ряда по первой, второй, третьей и четвертой гармониках (см. табл.
4, гр. 5, 8, 11 и 14) графически (рис. 1).
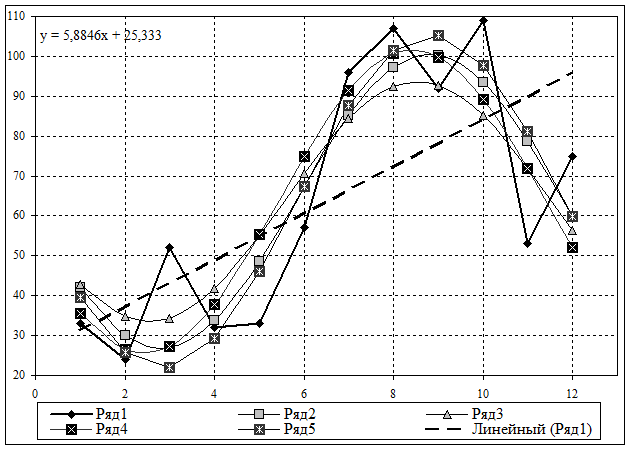Рис. 1. График объемов выпуска продукции предприятием за 12
месяцев года. Эмпирический ряд 1, первая гармоника выровненного ряда гр. 5
табл.4 – ряд 2, вторая гармоника выровненного ряда гр. 8 табл.4 – ряд 3, третья
гармоника выровненного ряда гр. 11 табл.4 – ряд 4, четвертая гармоника
выровненного ряда гр. 14 табл.4 – ряд 5
Анализ
результатов приводит к выводу о достаточности использования для выравнивания
только первой гармоники. Её значения являются усредненными по сравнению со
всеми перечисленными.
3.
Индексы сезонности.
Глубину
сезонных колебаний месячных данных измеряют индексами сезонности, которые
представляют собой отношение средних из фактических уровней одноименных месяцев
за рассматриваемый период к средней из выравненных данных по тем же месяцам
yсез. =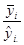 
,
(9)
где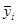 
-
средняя из фактических уровней i-того месяца за весь рассматриваемый период;
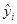- средний из
выравненных уровней i -того месяца, полученные либо
применением 12-месячной скользящей средней, либо аналитическим выравниваем.
Вычисление
индексов сезонности проиллюстрируем по данным полученной таблицы 4. Будем
полагать, что за 5-летний период были рассчитаны средние из фактических уровней
выпуска продукции предприятием за одноименные месяцы, затем производилось выравнивание ряда данных по
линейному тренду и рассчитывались средние из выравненных данных по каждому
месяцу (результаты расчетов приведены в табл. 5, гр. 3 и 4).
Таблица 5
|
п/п
|
Месяцы
|
Средний фактичесий
выпуск продукции за 5-летний
период, млн. руб.,
|
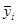
Средний выровненный по линейному
тренду уровень выпуска продукции,
|
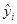
Индекс сезонности,
%
iсез.
|
(iсез.-100)2
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
Январь
|
33
|
31,2176
|
105,71
|
32,6
|
|
2
|
Февраль
|
24
|
37,1022
|
64,686
|
1247
|
|
3
|
Март
|
52
|
42,9868
|
120,97
|
439,6
|
|
4
|
Апрель
|
32
|
48,8714
|
65,478
|
1192
|
|
5
|
Май
|
33
|
54,756
|
60,267
|
1579
|
|
6
|
Июнь
|
57
|
60,6406
|
93,996
|
36,04
|
|
7
|
Июль
|
96
|
66,5252
|
144,31
|
1963
|
|
8
|
Август
|
107
|
72,4098
|
147,77
|
2282
|
|
9
|
Сентябрь
|
92
|
78,2944
|
117,51
|
306,4
|
|
10
|
Октябрь
|
109
|
84,179
|
129,49
|
869,4
|
|
11
|
Январь
|
53
|
90,0636
|
58,847
|
1694
|
|
12
|
Февраль
|
75
|
95,9482
|
78,167
|
476,7
|
|
|
|
|
|
s сез.=
|
31,78
|
Обобщающим
показателем изменений динамического ряда из-за сезонного характера производства
является среднее квадратическое отклонение индексов сезонности
s сез.=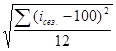 
.
Расчет s сез
основан па результатах, представленных в гр. 6 табл. 5, и составляет
31,78 %.
Сравнение средних квадратических
отклонений, вычисленных за разные периоды, показывает сдвиги в сезонности.
Уменьшение s сез свидетельствует об уменьшении влияния
сезонности на динамику анализируемого показателя.
Выводы.
Основные выводы содержатся в каждом пункте
выполнения задания.
Варианты
заданий. Варианты указаны римскими
цифрами в лабораторной № 4. Выбрать двенадцать (и более) признаков
динамического ряда из предложенного преподавателем варианта.