Лабораторная работа № 5. РЯДЫ ДИНАМИКИ. ЭКСТРАПОЛИРОВАНИЕ РЯДОВ  С ПОМОЩЬЮ КОЭФФИЦИЕНТА РОСТА, СРАВНЕНИЕ С ТРЕНДОВЫМИ ПОКАЗАТЕЛЯМИ. СЕЗОННАЯ НЕРАВНОМЕРНОСТЬ.

Цель работы: Анализ тенденции развития показателей динамических рядов во времени и выделение составляющих сезонной неравномерности.

Задание.  Используя данные о выпуске продукции предприятием за девять месяцев (см. табл.1) выделить основной тренд, сезонную и случайные компоненты динамического ряда. Продолжить ряд на последующие три месяца работы предприятия, используя данные об основной тенденции развития с применением коэффициента роста. Сравнить полученные результаты с основным и полиномиальными трендами. Представить динамические ряды графически.

Условие.  Имеются сведения о произведенной продукции предприятием в течение девяти месяцев (табл. 1).

Таблица 1

Месяцы, п/п	Выпуск продукции, млн. руб.
1	2
1	3,50
2	15,70
3	9,10
4	18,00
5	22,20
6	12,60
7	16,40
8	24,00
9	12,60

Выполнение задания.

1.         Выделение основного тренда, сезонной и случайной компонент динамического ряда

Признаки ряда динами существенно зависят от закономерных и случайных явлений.

Можно выделить наличие трех важнейших факторов признаков временного ряда: тренд, сезонную и случайную компоненты. На рис. 1 показаны вышеназванные факторы, представленные случайными и сезонными кривыми уровней временного ряда при наличии общей тенденции их повышения.

В широком понимании к сезонным процессам относятся все явления, которые обнаруживают в своем развитии отчетливо выраженную закономерность внутригодичных изменений, т.е. более или менее устойчиво повторяющиеся из года в год колебания уровней. Часто эти закономерности могут быть не связаны со сменой времен года. К сезонным явлениям относят, например, потребление электроэнергии; неравномерность производственной деятельности в отраслях пищевой промышленности, связанных с переработкой сельскохозяйственного сырья; перевозки пассажирским транспортом, спрос на многие виды продукции и услуг и т.д.

Как бы ни проявлялась сезонность, она наносит больше ущерб национальной экономике, связанный с неравномерным использованием оборудования и рабочей силы, с неравномерной; загрузкой транспорта, необходимостью создания резервов мощностей и т.д. Комплексное регулирование сезонных изменений отдельными отраслями должно основываться на статистическом исследовании сезонных отклонений.

 

Рис. 1. Эмпирические данные о произведенной продукции предприятием в течение девяти месяцев работы  – кривая 1, основной линейный тренд – кривая 2, сезонная кривая уровней временного ряда – кривая 3, кривая случайных признаков динамического ряда – 4.

2.         Определение среднемесячного темпа роста (снижения).

Средний коэффициент роста вычисляется по формуле

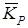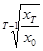 =  .                                                                  (1)

Из анализа кривой  2 (рис.1) основная тенденции развития производства на предприятии за девять проработанных месяцев возрастающая прямая, поэтому средний коэффициент роста, вычисленный по формуле (1) больше единицы и равен 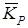 = = 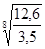1,1736 .

Продолжим таблицу 1, последовательно умножая соответствующие признаки динамического ряда на коэффициент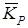

Таблица 2

Месяцы, п/п	Выпуск продукции, млн. руб.
1	2
1	3,5
2	15,7
3	9,1
4	18,0
5	22,2
6	12,6
7	16,4
8	24,0
9	12,6
10	14,8
11	17,4
12	20,4

Представим полученные данные графически (рис. 2).

Рис. 2. Эмпирические кривая произведенной продукции предприятием в течение девяти месяцев работы вместе с экстраполированными данными последующих трех месяцев, основной линейный тренд

3.         Сравнительная оценка с полиномиальными и основным трендами.

Для сравнительной характеристики общей закономерности ряда динамики вычислим новые значения, используя представленные на рис. 1 интерполированные функции  у₁ ,  у₂ ,  у₃ . Заполним таблицу 3. Графы 1 и 2 состоят из исходных данных и данных табл. 2, в графах 3, 6, 9 представлены значения функций от соответствующих параметров k_i (i =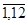). В столбцах 4, 7, 10  - разность между эмпирическими параметрами и интерполированными. Cреднее квадратическое отклонение от тренда вычисляется по формуле

S_yx = 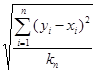,                                                         (2)

где  k = k(n) ,  n – число рассматриваемых месяцев.

Таблица  3

Месяцы, п/п	Выпуск продукции, млн. руб.	y2 = 1,175x + 9,025	y3 = 0,0194x3 - 0,7661x2 + 7,1551x - 0,973	y4 = -0,0429x6 + 1,262x5 - 14,507x4 + 82,303x3 - 239,5x2 + 334,83x - 160,7
ki	xi	y2i	y2i- xi	(y2i- xi)2	y3i	y3i- xi	(y3i- xi)2	y4i	y4i- xi	(y4i- xi)2
1	2	3	4	5	6	7	8	9	10	11
1	3,50	10,20	6,70	44,89	5,44	1,94	3,75	3,65	0,15	0,02
2	15,70	11,38	-4,33	18,71	10,43	-5,27	27,79	14,91	-0,79	0,62
3	9,10	12,55	3,45	11,90	14,12	5,02	25,21	10,80	1,70	2,88
4	18,00	13,73	-4,28	18,28	16,63	-1,37	1,87	16,79	-1,21	1,47
5	22,20	14,90	-7,30	53,29	18,08	-4,13	17,02	20,39	-1,81	3,29
6	12,60	16,08	3,48	12,08	18,57	5,97	35,62	15,52	2,92	8,53
7	16,40	17,25	0,85	0,72	18,23	1,83	3,34	14,64	-1,76	3,10
8	24,00	18,43	-5,58	31,08	17,17	-6,83	46,65	25,07	1,07	1,14
9	12,60	19,60	7,00	49,00	15,51	2,91	8,48	12,63	0,03	0,00
		Cреднее квадратическое отклонение от тренда	5,16	Cреднее квадратическое отклонение от тренда	4,34	Cреднее квадратическое отклонение от тренда	1,53
10	14,79	20,78	5,99	35,84	164,64	149,85	22456,28	-229,40	-244,19	59627,76
11	17,36	21,95	4,59	21,11	-8,83	-26,18	685,65	-1062,37	-1079,72	1165805,56
12	20,37	23,13	2,76	7,59	17,68	-2,69	7,23	-3301,04	-3321,41	11031746,25
		Cреднее квадратическое отклонение от тренда	5,04	Cреднее квадратическое отклонение от тренда	44,08	Cреднее квадратическое отклонение от тренда	1010,66

Выводы.

Основная закономерность исследуемого динамического ряда имеет тенденцию к возрастанию, сезонные факторы обладают четко выраженной вершиной, случайные процессы – тремя вершинами.

Анализ таблицы 3 позволяет сделать существенное замечание о том, что интерполирование эмпирических параметров тем точнее, чем выше степень тренда (полинома). В качестве функции экстраполяции лучше выбрать линейный тренд.

Эти методы могут быть использованы для оценки тенденций развития различных общественных явлений.

Варианты заданий.  Варианты указаны римскими цифрами в лабораторной № 4. Продолжить динамический ряд, дополнив его тремя значениями.